Difference between revisions of "Normal space"
(Importing text file) |
(LaTeX) |
||
| Line 1: | Line 1: | ||
| − | A [[Topological space|topological space]] satisfying the axiom | + | A [[Topological space|topological space]] satisfying the axiom $T_4$ (see [[Separation axiom|Separation axiom]]), that is, one in which one-point sets are closed and any two disjoint closed sets can be separated by neighbourhoods (that is, are contained in disjoint open sets). Normal spaces form a special case of completely-regular spaces (Tikhonov spaces, cf. [[Completely-regular space|Completely-regular space]]) and are particularly important in [[Dimension theory|dimension theory]]. Every closed subspace of a normal space is normal (normality is hereditary over closed sets). Spaces all subspaces of which are normal are said to be hereditarily normal. For hereditary normality of a space it is sufficient that all its open subspaces are normal, and it is necessary and sufficient that any two sets none of which contains an adherence point of the other are separable by neighbourhoods. A normal space is called perfectly normal if every closed set in it is the intersection of countably many open sets. Every perfectly-normal space is a hereditarily-normal space. |
The product of two normal spaces need not be normal, and even the product of a normal space and a segment may be non-normal. | The product of two normal spaces need not be normal, and even the product of a normal space and a segment may be non-normal. | ||
| − | There are important classes of spaces that are more general than normal and less general than completely regular. First among such spaces close to normal were the so-called quasi-normal, or | + | There are important classes of spaces that are more general than normal and less general than completely regular. First among such spaces close to normal were the so-called quasi-normal, or $\pi$-normal, ones [[#References|[2]]]. These are Tikhonov spaces in which any two disjoint $\pi$-sets can be separated by neighbourhoods. $\pi$-sets are intersections of finitely many closed canonical sets (cf. [[Canonical set|Canonical set]]). Tikhonov spaces in which any two disjoint closed canonical sets can be separated by neighbourhoods are called $\kappa$-normal [[#References|[3]]]; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067660/n0676609.png" />-normal spaces in which every closed canonical set is the intersection of countably many open canonical sets are called perfectly $\kappa$-normal. The classes of Tikhonov $\kappa$-normal, quasi-normal and perfectly $\kappa$-normal spaces are successively contained in each other and no two of them are equal. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.I. Zaitsev, "On the theory of Tikhonov spaces" ''Vestnik Moskov. Univ. Mat. Mekh.'' : 3 (1967) pp. 48–57 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.V. Shchepin, "Real functions and near-normal spaces" ''Sib. Math. J.'' , '''13''' : 5 (1972) pp. 820–830 ''Sibirsk. Mat. Zh.'' , '''13''' : 5 (1972) pp. 1182–1196</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> V.I. Zaitsev, "On the theory of Tikhonov spaces" ''Vestnik Moskov. Univ. Mat. Mekh.'' : 3 (1967) pp. 48–57 (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> E.V. Shchepin, "Real functions and near-normal spaces" ''Sib. Math. J.'' , '''13''' : 5 (1972) pp. 820–830 ''Sibirsk. Mat. Zh.'' , '''13''' : 5 (1972) pp. 1182–1196</TD></TR> | ||
| + | </table> | ||
| Line 13: | Line 17: | ||
Normal spaces are also characterized by the following two statements: | Normal spaces are also characterized by the following two statements: | ||
| − | 1) Urysohn's lemma: If | + | 1) Urysohn's lemma: If $A,B \subseteq X$ are closed and disjoint, then there is a continuous function $f : X \rightarrow [0,1]$ such that $f \downharpoonright_A = \{0\}$ and $f \downharpoonright_B = \{1\}$. In other words, any two closed sets can be separated by a continuous function. |
| − | 2) The Tietze–Urysohn extension theorem: If | + | 2) The Tietze–Urysohn extension theorem: If $A \subseteq X$ is closed and $f : A \rightarrow [0,1]$ is continuous, then $f$ can be extended to a continuous $\bar f : X \rightarrow [0,1]$. |
| − | A normal space | + | A normal space $X$ such that $X \times [0,1]$ is not normal, a so-called Dowker space, was constructed by M.E. Rudin [[#References|[a3]]]. |
| − | A space | + | A space $X$ is called collection-wise normal if for every discrete family of subsets $\{ F_\alpha : \alpha \in A \}$ there exists a discrete family $\{ U_\alpha : \alpha \in A \}$ of open sets in $X$ such that $F_\alpha \subset U_\alpha$ for all $\alpha \in A$. Here a family of subsets $\{ Y_\alpha : \alpha \in A \}$ is called a discrete family if for every $x \in X$ there is an open neighbourhood $U_x$ such that $U_x$ intersects at most one $Y_\alpha$. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Engelking, "General topology" , PWN (1977) (Translated from Polish) (Revised and extended version of [3] above)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M.E. Rudin, "A normal space | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Engelking, "General topology" , PWN (1977) (Translated from Polish) (Revised and extended version of [3] above)</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> M.E. Rudin, "A normal space $X$ for which $X \times I$ is not normal" ''Fund. Math.'' , '''73''' (1971) pp. 179–186</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> R.A. Alò, H.L. Shapiro, "Normal topological spaces" , Cambridge Univ. Press (1974)</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|done}} | ||
Revision as of 21:05, 31 October 2014
A topological space satisfying the axiom $T_4$ (see Separation axiom), that is, one in which one-point sets are closed and any two disjoint closed sets can be separated by neighbourhoods (that is, are contained in disjoint open sets). Normal spaces form a special case of completely-regular spaces (Tikhonov spaces, cf. Completely-regular space) and are particularly important in dimension theory. Every closed subspace of a normal space is normal (normality is hereditary over closed sets). Spaces all subspaces of which are normal are said to be hereditarily normal. For hereditary normality of a space it is sufficient that all its open subspaces are normal, and it is necessary and sufficient that any two sets none of which contains an adherence point of the other are separable by neighbourhoods. A normal space is called perfectly normal if every closed set in it is the intersection of countably many open sets. Every perfectly-normal space is a hereditarily-normal space.
The product of two normal spaces need not be normal, and even the product of a normal space and a segment may be non-normal.
There are important classes of spaces that are more general than normal and less general than completely regular. First among such spaces close to normal were the so-called quasi-normal, or $\pi$-normal, ones [2]. These are Tikhonov spaces in which any two disjoint $\pi$-sets can be separated by neighbourhoods. $\pi$-sets are intersections of finitely many closed canonical sets (cf. Canonical set). Tikhonov spaces in which any two disjoint closed canonical sets can be separated by neighbourhoods are called $\kappa$-normal [3]; 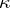 -normal spaces in which every closed canonical set is the intersection of countably many open canonical sets are called perfectly $\kappa$-normal. The classes of Tikhonov $\kappa$-normal, quasi-normal and perfectly $\kappa$-normal spaces are successively contained in each other and no two of them are equal.
-normal spaces in which every closed canonical set is the intersection of countably many open canonical sets are called perfectly $\kappa$-normal. The classes of Tikhonov $\kappa$-normal, quasi-normal and perfectly $\kappa$-normal spaces are successively contained in each other and no two of them are equal.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [2] | V.I. Zaitsev, "On the theory of Tikhonov spaces" Vestnik Moskov. Univ. Mat. Mekh. : 3 (1967) pp. 48–57 (In Russian) |
| [3] | E.V. Shchepin, "Real functions and near-normal spaces" Sib. Math. J. , 13 : 5 (1972) pp. 820–830 Sibirsk. Mat. Zh. , 13 : 5 (1972) pp. 1182–1196 |
Comments
Normal spaces are also characterized by the following two statements:
1) Urysohn's lemma: If $A,B \subseteq X$ are closed and disjoint, then there is a continuous function $f : X \rightarrow [0,1]$ such that $f \downharpoonright_A = \{0\}$ and $f \downharpoonright_B = \{1\}$. In other words, any two closed sets can be separated by a continuous function.
2) The Tietze–Urysohn extension theorem: If $A \subseteq X$ is closed and $f : A \rightarrow [0,1]$ is continuous, then $f$ can be extended to a continuous $\bar f : X \rightarrow [0,1]$.
A normal space $X$ such that $X \times [0,1]$ is not normal, a so-called Dowker space, was constructed by M.E. Rudin [a3].
A space $X$ is called collection-wise normal if for every discrete family of subsets $\{ F_\alpha : \alpha \in A \}$ there exists a discrete family $\{ U_\alpha : \alpha \in A \}$ of open sets in $X$ such that $F_\alpha \subset U_\alpha$ for all $\alpha \in A$. Here a family of subsets $\{ Y_\alpha : \alpha \in A \}$ is called a discrete family if for every $x \in X$ there is an open neighbourhood $U_x$ such that $U_x$ intersects at most one $Y_\alpha$.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [a2] | R. Engelking, "General topology" , PWN (1977) (Translated from Polish) (Revised and extended version of [3] above) |
| [a3] | M.E. Rudin, "A normal space $X$ for which $X \times I$ is not normal" Fund. Math. , 73 (1971) pp. 179–186 |
| [a4] | R.A. Alò, H.L. Shapiro, "Normal topological spaces" , Cambridge Univ. Press (1974) |
Normal space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_space&oldid=34133