Difference between revisions of "Complete lattice"
m (→Comments: better) |
(→References: Davey & Priestley (2002)) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian)</TD></TR> | ||
| + | </table> | ||
| Line 8: | Line 11: | ||
====Comments==== | ====Comments==== | ||
For the topic "closure operation" , cf. also [[Closure relation|Closure relation]]; [[Basis|Basis]]. | For the topic "closure operation" , cf. also [[Closure relation|Closure relation]]; [[Basis|Basis]]. | ||
| + | |||
| + | ====References==== | ||
| + | <table> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> B. A. Davey, H. A. Priestley, ''Introduction to lattices and order'', 2nd ed. Cambridge University Press (2002) ISBN 978-0-521-78451-1</TD></TR> | ||
| + | </table> | ||
Revision as of 15:26, 18 October 2014
A partially ordered set in which any subset 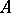 has a least upper bound and a greatest lower bound. These are usually called the join and the meet of
has a least upper bound and a greatest lower bound. These are usually called the join and the meet of 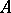 and are denoted by
and are denoted by 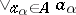 and
and  or simply by
or simply by  and
and 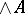 (respectively). If a partially ordered set has a largest element and each non-empty subset of it has a greatest lower bound, then it is a complete lattice. A lattice
(respectively). If a partially ordered set has a largest element and each non-empty subset of it has a greatest lower bound, then it is a complete lattice. A lattice  is complete if and only if any isotone mapping
is complete if and only if any isotone mapping 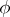 of the lattice into itself has a fixed point, i.e. an element
of the lattice into itself has a fixed point, i.e. an element 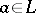 such that
such that 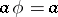 . If
. If 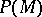 is the set of subsets of a set
is the set of subsets of a set 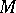 ordered by inclusion and
ordered by inclusion and 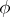 is a closure operation on
is a closure operation on 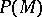 , then the set of all
, then the set of all 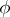 -closed subsets is a complete lattice. Any partially ordered set
-closed subsets is a complete lattice. Any partially ordered set 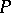 can be isomorphically imbedded in a complete lattice, which in that case is called a completion of
can be isomorphically imbedded in a complete lattice, which in that case is called a completion of 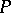 . The completion by sections (cf. Completion, MacNeille (of a partially ordered set)) is the least of all completions of a given partially ordered set. Complete lattices are formed by the set of all subalgebras in a universal algebra, by the set of all congruences in a universal algebra, and by the set of all closed subsets in a topological space.
. The completion by sections (cf. Completion, MacNeille (of a partially ordered set)) is the least of all completions of a given partially ordered set. Complete lattices are formed by the set of all subalgebras in a universal algebra, by the set of all congruences in a universal algebra, and by the set of all closed subsets in a topological space.
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian) |
Comments
For the topic "closure operation" , cf. also Closure relation; Basis.
References
| [a1] | B. A. Davey, H. A. Priestley, Introduction to lattices and order, 2nd ed. Cambridge University Press (2002) ISBN 978-0-521-78451-1 |
Complete lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_lattice&oldid=33805