Difference between revisions of "Stokes phenomenon"
(Importing text file) |
m |
||
| Line 1: | Line 1: | ||
| + | {{DEF}} | ||
| + | |||
The property that a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903201.png" /> may have different asymptotic expressions when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903202.png" /> in different domains of the complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903203.png" />-plane. G. Stokes demonstrated [[#References|[1]]] that the solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903204.png" /> of the so-called [[Airy equation|Airy equation]] | The property that a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903201.png" /> may have different asymptotic expressions when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903202.png" /> in different domains of the complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903203.png" />-plane. G. Stokes demonstrated [[#References|[1]]] that the solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090320/s0903204.png" /> of the so-called [[Airy equation|Airy equation]] | ||
Revision as of 14:41, 19 May 2012
This page is deficient and requires revision. Please see Talk:Stokes phenomenon for further comments.
The property that a function  may have different asymptotic expressions when
may have different asymptotic expressions when 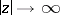 in different domains of the complex
in different domains of the complex  -plane. G. Stokes demonstrated [1] that the solution
-plane. G. Stokes demonstrated [1] that the solution  of the so-called Airy equation
of the so-called Airy equation
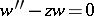 |
which decreases for real 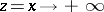 , has the following asymptotic expansion when
, has the following asymptotic expansion when 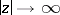 :
:
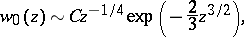 |
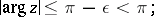 |
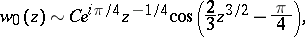 |
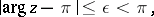 |
where 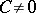 is a constant. The function
is a constant. The function 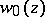 is an entire function, while its asymptotic expansion is a discontinuous function.
is an entire function, while its asymptotic expansion is a discontinuous function.
The Stokes phenomenon also occurs for Laplace integrals, solutions of ordinary differential equations, etc. (see [2], [3]).
References
| [1] | G.G. Stokes, Trans. Cambridge Philos. Soc. , 10 (1864) pp. 106–128 |
| [2] | J. Heading, "An introduction to phase-integral methods" , Methuen (1962) |
| [3] | N.G. de Bruijn, "Asymptotic methods in analysis" , Dover, reprint (1981) |
Comments
There is a recent interest in the Stokes phenomenon in asymptotic analysis, which is initiated by M.V. Berry in [a1]. In the new interpretation of the phenomenon, an error function is introduced to describe the rapid change in the behaviour of the remainders of the asymptotic expansions as a Stokes line is crossed. A rigorous treatment of Berry's observation is given in [a2].
References
| [a1] | M.V. Berry, "Uniform asymptotic smoothing of Stokes' discontinuities" Proc. R. Soc. London A , 422 (1989) pp. 7–21 |
| [a2] | "On Stokes's phenomenon and converging factors" R. Wong (ed.) , Proc. Int. Symp. Asymptotic and Computational Anal. (Winnipeg, Manitoba) , M. Dekker (1990) |
Stokes phenomenon. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stokes_phenomenon&oldid=26717