Difference between revisions of "Riemann theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
Riemann's theorem on conformal mappings: Given any two simply-connected domains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820801.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820802.png" /> of the extended complex plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820803.png" />, distinct from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820804.png" /> and also from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820805.png" /> with a point excluded from it, then an infinite number of analytic single-valued functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820806.png" /> can be found such that each one realizes a one-to-one conformal transformation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820807.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820808.png" />. In this case, for any pair of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820809.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208010.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208011.png" /> and any real number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208013.png" />, a unique function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208014.png" /> of this class can be found for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208016.png" />. The condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208017.png" /> geometrically means that each infinitely-small vector emanating from the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208018.png" /> changes under the transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208019.png" /> into an infinitely-small vector the direction of which forms with the direction of the original vector the angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208020.png" />. | Riemann's theorem on conformal mappings: Given any two simply-connected domains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820801.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820802.png" /> of the extended complex plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820803.png" />, distinct from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820804.png" /> and also from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820805.png" /> with a point excluded from it, then an infinite number of analytic single-valued functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820806.png" /> can be found such that each one realizes a one-to-one conformal transformation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820807.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820808.png" />. In this case, for any pair of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r0820809.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208010.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208011.png" /> and any real number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208013.png" />, a unique function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208014.png" /> of this class can be found for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208016.png" />. The condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208017.png" /> geometrically means that each infinitely-small vector emanating from the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208018.png" /> changes under the transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208019.png" /> into an infinitely-small vector the direction of which forms with the direction of the original vector the angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208020.png" />. | ||
| − | Riemann's theorem is fundamental in the theory of [[Conformal mapping|conformal mapping]] and in the geometrical theory of functions of a complex variable in general. In addition to its generalizations to multiply-connected domains, it finds wide application in the theory of functions of a complex variable, in mathematical physics, in the theory of elasticity, in aero- and hydromechanics, in electro- and magnetostatics, etc. This theorem was formulated by B. Riemann (1851) for the more general case of simply-connected and, generally speaking, non-single sheeted domains over the complex plane. Instead of using the normalizing conditions | + | Riemann's theorem is fundamental in the theory of [[Conformal mapping|conformal mapping]] and in the geometrical theory of functions of a complex variable in general. In addition to its generalizations to multiply-connected domains, it finds wide application in the theory of functions of a complex variable, in mathematical physics, in the theory of elasticity, in aero- and hydromechanics, in electro- and magnetostatics, etc. This theorem was formulated by B. Riemann (1851) for the more general case of simply-connected and, generally speaking, non-single sheeted domains over the complex plane. Instead of using the normalizing conditions "fa= b, argf'a=a" of the conformal mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208021.png" />, which guarantee its uniqueness, Riemann used for the same purpose the conditions "fa= b, fz=w" , where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208022.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208025.png" /> are points of the boundaries of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208027.png" />, respectively, given in advance. The last conditions are not always correct, given the contemporary definition of a simply-connected domain. In proving his theorem, Riemann drew to a considerable degree on concepts of physics, which also convinced him of the importance of this theorem for applications. D. Hilbert made Riemann's proof mathematically precise by substantiating the so-called [[Dirichlet principle|Dirichlet principle]], which was used by Riemann in his proof. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Riemann, "Gesammelte mathematischen Abhandlungen" , Dover, reprint (1953)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , '''1–3''' , Teubner (1958–1959) (Translated from Russian) {{MR|0342680}} {{MR|0264037}} {{MR|0264036}} {{MR|0264038}} {{MR|0123686}} {{MR|0123685}} {{MR|0098843}} {{ZBL|0177.33401}} {{ZBL|0141.26003}} {{ZBL|0141.26002}} {{ZBL|0082.28802}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian) {{MR|0247039}} {{ZBL|0183.07502}} </TD></TR></table> |
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Z. Nehari, "Conformal mapping" , Dover, reprint (1975) {{MR|0377031}} {{ZBL|0071.07301}} {{ZBL|0052.08201}} {{ZBL|0048.31503}} {{ZBL|0041.41201}} </TD></TR></table> |
Riemann's theorem on the rearrangement of terms of a series: If a series in which the terms are real numbers converges but does not converge absolutely, then for any number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208028.png" /> there is a rearrangement of the terms of this series such that the sum of the series obtained will be equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208029.png" />. Furthermore, there is a rearrangement of the terms of the series such that its sum will be equal to one of the previously given signed infinities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208030.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208031.png" />, and also such that its sum will not be equal either to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208032.png" /> or to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208033.png" />, but the sequences of its partial sums have given liminf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208034.png" /> and limsup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208035.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208036.png" /> (see [[Series|Series]]). | Riemann's theorem on the rearrangement of terms of a series: If a series in which the terms are real numbers converges but does not converge absolutely, then for any number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208028.png" /> there is a rearrangement of the terms of this series such that the sum of the series obtained will be equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208029.png" />. Furthermore, there is a rearrangement of the terms of the series such that its sum will be equal to one of the previously given signed infinities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208030.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208031.png" />, and also such that its sum will not be equal either to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208032.png" /> or to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208033.png" />, but the sequences of its partial sums have given liminf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208034.png" /> and limsup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208035.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082080/r08208036.png" /> (see [[Series|Series]]). | ||
| Line 22: | Line 22: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) {{MR|0028430}} {{ZBL|0124.28302}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 75–78 {{MR|0385023}} {{ZBL|0346.26002}} </TD></TR></table> |
====Comments==== | ====Comments==== | ||
| − | Another | + | Another "Riemann theorem" is the Riemann removable singularities theorem, see [[Removable set|Removable set]]. |
Revision as of 17:01, 15 April 2012
Riemann's theorem on conformal mappings: Given any two simply-connected domains  and
and  of the extended complex plane
of the extended complex plane  , distinct from
, distinct from  and also from
and also from  with a point excluded from it, then an infinite number of analytic single-valued functions on
with a point excluded from it, then an infinite number of analytic single-valued functions on  can be found such that each one realizes a one-to-one conformal transformation of
can be found such that each one realizes a one-to-one conformal transformation of  onto
onto  . In this case, for any pair of points
. In this case, for any pair of points  ,
,  , and
, and  and any real number
and any real number 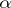 ,
, 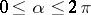 , a unique function
, a unique function 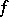 of this class can be found for which
of this class can be found for which  ,
,  . The condition
. The condition  geometrically means that each infinitely-small vector emanating from the point
geometrically means that each infinitely-small vector emanating from the point  changes under the transformation
changes under the transformation  into an infinitely-small vector the direction of which forms with the direction of the original vector the angle
into an infinitely-small vector the direction of which forms with the direction of the original vector the angle  .
.
Riemann's theorem is fundamental in the theory of conformal mapping and in the geometrical theory of functions of a complex variable in general. In addition to its generalizations to multiply-connected domains, it finds wide application in the theory of functions of a complex variable, in mathematical physics, in the theory of elasticity, in aero- and hydromechanics, in electro- and magnetostatics, etc. This theorem was formulated by B. Riemann (1851) for the more general case of simply-connected and, generally speaking, non-single sheeted domains over the complex plane. Instead of using the normalizing conditions "fa= b, argf'a=a" of the conformal mapping  , which guarantee its uniqueness, Riemann used for the same purpose the conditions "fa= b, fz=w" , where
, which guarantee its uniqueness, Riemann used for the same purpose the conditions "fa= b, fz=w" , where 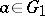 ,
,  and
and 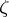 and
and 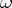 are points of the boundaries of
are points of the boundaries of 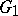 and
and  , respectively, given in advance. The last conditions are not always correct, given the contemporary definition of a simply-connected domain. In proving his theorem, Riemann drew to a considerable degree on concepts of physics, which also convinced him of the importance of this theorem for applications. D. Hilbert made Riemann's proof mathematically precise by substantiating the so-called Dirichlet principle, which was used by Riemann in his proof.
, respectively, given in advance. The last conditions are not always correct, given the contemporary definition of a simply-connected domain. In proving his theorem, Riemann drew to a considerable degree on concepts of physics, which also convinced him of the importance of this theorem for applications. D. Hilbert made Riemann's proof mathematically precise by substantiating the so-called Dirichlet principle, which was used by Riemann in his proof.
References
| [1] | B. Riemann, "Gesammelte mathematischen Abhandlungen" , Dover, reprint (1953) |
| [2] | I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , 1–3 , Teubner (1958–1959) (Translated from Russian) MR0342680 MR0264037 MR0264036 MR0264038 MR0123686 MR0123685 MR0098843 Zbl 0177.33401 Zbl 0141.26003 Zbl 0141.26002 Zbl 0082.28802 |
| [3] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) MR0247039 Zbl 0183.07502 |
Comments
This theorem is also called the Riemann mapping theorem.
References
| [a1] | Z. Nehari, "Conformal mapping" , Dover, reprint (1975) MR0377031 Zbl 0071.07301 Zbl 0052.08201 Zbl 0048.31503 Zbl 0041.41201 |
Riemann's theorem on the rearrangement of terms of a series: If a series in which the terms are real numbers converges but does not converge absolutely, then for any number  there is a rearrangement of the terms of this series such that the sum of the series obtained will be equal to
there is a rearrangement of the terms of this series such that the sum of the series obtained will be equal to  . Furthermore, there is a rearrangement of the terms of the series such that its sum will be equal to one of the previously given signed infinities
. Furthermore, there is a rearrangement of the terms of the series such that its sum will be equal to one of the previously given signed infinities  or
or  , and also such that its sum will not be equal either to
, and also such that its sum will not be equal either to  or to
or to  , but the sequences of its partial sums have given liminf
, but the sequences of its partial sums have given liminf 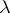 and limsup
and limsup 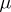 , with
, with 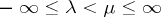 (see Series).
(see Series).
L.D. Kudryavtsev
Comments
References
| [a1] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) MR0028430 Zbl 0124.28302 |
| [a2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 75–78 MR0385023 Zbl 0346.26002 |
Comments
Another "Riemann theorem" is the Riemann removable singularities theorem, see Removable set.
Riemann theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_theorem&oldid=24555