Difference between revisions of "Künneth formula"
| Line 391: | Line 391: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Hodgkin, "The equivariant Künneth theorem in | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Hodgkin, "The equivariant Künneth theorem in $K$-theory" , ''Lect. notes in math.'' , '''496''' , Springer (1975)</TD></TR> | ||
| + | </table> | ||
Revision as of 05:56, 19 July 2024
A formula expressing the homology (or cohomology) of a tensor product of complexes or a direct product of spaces in terms of the homology (or cohomology) of the factors.
Let $ \Lambda $ be an associative ring with a unit (cf. Associative rings and algebras), and let $ A $ and $ C $ be chain complexes of right and left $ \Lambda $- modules, respectively. Let $ A \otimes C $ be the complex associated with the tensor product of $ A $ and $ C $ over $ \Lambda $. If
$$ \mathop{\rm Tor} _ {1} ( B ( A), B ( C)) = \ \mathop{\rm Tor} _ {1} ( H _ {*} ( A), B ( C)) = $$
$$ = \ \mathop{\rm Tor} _ {1} ( B ( A), Z ( C)) = \mathop{\rm Tor} _ {1} ( H _ {*} ( A), Z ( C)) = 0, $$
then there is an exact sequence of graded modules
$$ \tag{1 } 0 \rightarrow H _ {*} ( A) \otimes H _ {*} ( C) \mathop \rightarrow \limits ^ \alpha \ H _ {*} ( A \otimes C) \mathop \rightarrow \limits ^ \beta \ $$
$$ \mathop \rightarrow \limits ^ \beta \mathop{\rm Tor} _ {1} ( H _ {*} ( A), H _ {*} ( C)) \rightarrow 0, $$
where $ \alpha $ and $ \beta $ are homomorphisms of degree 0 and $ - 1 $, respectively (see [2]). There is an analogous exact sequence for cochain complexes, with a homomorphism $ \beta $ of degree 1. If $ H _ {*} ( \mathop{\rm Tor} _ {1} ( A, C)) = 0 $( e.g. $ A $ or $ C $ is a flat $ \Lambda $- module) and $ \Lambda $ is hereditary, the sequence (1) exists and splits [2], [3], so that
$$ H _ {n} ( A \otimes C) = \ \sum _ {p + q = n } H _ {p} ( A) \otimes H _ {q} ( C) + $$
$$ + \sum _ {p + q = n - 1 } \mathop{\rm Tor} _ {1} ( H _ {p} ( A), H _ {q} ( C)). $$
This is the Künneth formula; the term Künneth formula (or Künneth relation) is sometimes also applied to the exact sequence (1). There is a generalization of (1) in which the tensor product is replaced by an arbitrary two-place functor $ T( A, C) $, on the category of $ \Lambda $- modules with values in the same category, that is covariant in $ A $ and contravariant in $ C $. In particular, the functor $ T ( A, C) = \mathop{\rm Hom} ( A, C) $ yields a formula expressing the cohomology $ H ^ {*} ( \mathop{\rm Hom} ( A, C)) $, where $ A $ is a right chain complex and $ C $ a left cochain complex over $ \Lambda $, in terms of $ H _ {*} ( A) $ and $ H ^ {*} ( C) $. Indeed, if $ \Lambda $ is hereditary and $ H ^ {*} ( \mathop{\rm Ext} ^ {1} ( A, C) ) = 0 $( e.g. $ A $ is free), one has the split exact sequence
$$ 0 \rightarrow \mathop{\rm Ext} ^ {1} ( H _ {*} ( A),\ H ^ {*} ( C)) \rightarrow ^ { {\beta ^ \prime } } \ H ^ {*} ( \mathop{\rm Hom} ( A, C)) \rightarrow ^ { {\alpha ^ \prime } } \ $$
$$ \rightarrow ^ { {\alpha ^ \prime } } \mathop{\rm Hom} ( H _ {*} ( A), H ^ {*} ( C)) \rightarrow 0, $$
where $ \alpha ^ \prime $ and $ \beta ^ \prime $ are homomorphisms of degree 0 and 1, respectively (see [2], [3]).
Let $ X $, $ Y $ be topological spaces and let $ L $, $ M $ be modules over a principal ideal ring $ R $ such that $ \mathop{\rm Tor} _ {1} ( L, M) = 0 $. Then the singular homologies of the spaces $ X $, $ Y $, $ X \times Y $ are connected by the following split exact sequence:
$$ 0 \rightarrow H _ {*} ( X, L) \otimes H _ {*} ( Y, M) \mathop \rightarrow \limits ^ \alpha H _ {*} ( X \times Y, L \otimes M) \mathop \rightarrow \limits ^ \beta $$
$$ \mathop \rightarrow \limits ^ \beta \mathop{\rm Tor} _ {1} ( H _ {*} ( X, L), H _ {*} ( Y, M)) \rightarrow 0, $$
where $ \alpha $ and $ \beta $ are homomorphisms of degree 0 and $ - 1 $, respectively. If one assumes in addition that either all $ H _ {k} ( X, R) $ and $ H _ {k} ( Y, R) $, or all $ H _ {k} ( Y, R) $ and $ M $, are finitely generated, an analogous exact sequence is valid for the singular cohomologies:
$$ 0 \rightarrow H ^ {*} ( X, L) \otimes H ^ {*} ( Y, M) \mathop \rightarrow \limits ^ \alpha \ H ^ {*} ( X \times Y, L \otimes M) \mathop \rightarrow \limits ^ \beta $$
$$ \mathop \rightarrow \limits ^ \beta \mathop{\rm Tor} _ {1} ( H ^ {*} ( X, L), H ^ {*} ( Y, M)) \rightarrow 0, $$
where $ \alpha $ and $ \beta $ are homomorphisms of degree 0 and 1, respectively. For example, if $ R $ is a field, then
$$ H _ {*} ( X \times Y, R) \cong \ H _ {*} ( X, R) \otimes H _ {*} ( Y, R), $$
and if it is also true that all $ H _ {k} ( X, R) $, or all $ H _ {k} ( Y, R) $, are finite-dimensional, then
$$ H ^ {*} ( X \times Y, R) \cong \ H ^ {*} ( X, R) \otimes H ^ {*} ( Y, R). $$
Similar formulas are available for the relative homology and cohomology [3], [4].
In the case $ L = M = R $, the module $ H ^ {*} ( X, R) \otimes H ^ {*} ( Y, R) $ has the structure of a skew tensor product (cf. Skew product) of algebras, with $ \alpha $ a homomorphism of algebras. Thus, if $ \mathop{\rm Tor} _ {1} ( H ^ {*} ( X, R), H ^ {*} ( Y, R)) = 0 $ and all $ H _ {k} ( X, R) $, or all $ H _ {k} ( Y, R) $, are finitely generated, one has the following isomorphism of algebras [3]:
$$ H ^ {*} ( X \times Y, R) \cong \ H ^ {*} ( X, R) \otimes H ^ {*} ( Y, R). $$
If $ X $ and $ Y $ are finite polyhedra, the Künneth formula enables one to find the Betti numbers and torsion coefficients of the polyhedron $ X \times Y $ in terms of the analogous invariants of $ X $ and $ Y $. These are in fact the original results of H. Künneth himself . In particular, if $ b _ {k} ( X) $ is the $ k $- th Betti number of the polyhedron $ X $ and if
$$ p ( X) = \sum _ {k \geq 0 } b _ {k} ( X) t ^ {k} $$
is its Poincaré polynomial, then $ p ( X \times Y) = p ( X) p ( Y) $.
In the theory of cohomology with values in a sheaf there is yet another variant of the Künneth formula [6]. Let $ X $ and $ Y $ be topological spaces with countable bases, and let $ {\mathcal F} $ and $ {\mathcal G} $ be Fréchet sheaves on $ X $ and $ Y $( see Coherent analytic sheaf). Suppose that $ {\mathcal F} $( or $ {\mathcal G} $) is a nuclear sheaf (i.e. $ {\mathcal F} ( U) $ is a nuclear space for all open $ U \subset X $). Then the Fréchet sheaf $ {\mathcal F} \widetilde \otimes {\mathcal G} $ is defined on $ X \times Y $ such that
$$ ( {\mathcal F} \widetilde \otimes {\mathcal G} ) ( U \times V) = \ {\mathcal F} ( U) \widetilde \otimes {\mathcal G} ( V), $$
where $ \widetilde \otimes $ is the symbol for the completed tensor product and $ U \subset X $, $ V \subset Y $ are open. If the spaces $ H ^ {*} ( X, {\mathcal F} ) $ and $ H ^ {*} ( Y, {\mathcal G} ) $ are separable, one has the Künneth formula
$$ H ^ {*} ( X \times Y, {\mathcal F} \widetilde \otimes {\mathcal G} ) \cong \ H ^ {*} ( X, {\mathcal F} ) \widetilde \otimes H ^ {*} ( Y, {\mathcal G} ). $$
In particular, coherent analytic sheaves $ {\mathcal F} $, $ {\mathcal G} $ on complex-analytic spaces $ X $, $ Y $ with countable bases are nuclear and
$$ {\mathcal F} \widetilde \otimes {\mathcal G} \cong \ {\mathcal F} ^ {*} \otimes _ { {\mathcal O} _ {X \times Y } } {\mathcal G} ^ {*} , $$
where $ {\mathcal F} ^ {*} $, $ {\mathcal G} ^ {*} $ are the analytic inverse images of $ {\mathcal F} $ and $ {\mathcal G} $ under the projections $ X \times Y \rightarrow X $ and $ X \times Y \rightarrow Y $. Thus, if $ H ^ {*} ( X, {\mathcal F} ) $ and $ H ^ {*} ( Y, {\mathcal G} ) $ are separable, then
$$ H ^ {*} \left ( X \times Y, {\mathcal F} ^ {*} \otimes _ { {\mathcal O} _ {X \times Y } } {\mathcal G} ^ {*} \right ) \cong \ H ^ {*} ( X, {\mathcal F} ) \widetilde \otimes H ^ {*} ( Y, {\mathcal G} ). $$
The Künneth formulas also figure in algebraic geometry, usually in the following version. Let $ X $ and $ Y $ be algebraic varieties over a field $ k $, and let $ {\mathcal F} $ and $ {\mathcal G} $ be coherent algebraic sheaves (cf. Coherent algebraic sheaf) on $ X $ and $ Y $, respectively. Then [9]:
$$ H ^ {*} \left ( X \times Y, {\mathcal F} \otimes _ { k } {\mathcal G} \right ) \cong \ H ^ {*} ( X, {\mathcal F} ) \otimes _ { k } H ^ {*} ( Y, {\mathcal G} ). $$
Here $ {\mathcal F} \otimes _ {k} {\mathcal G} $ is the sheaf on $ X \times Y $ whose modules of sections over $ U \times V $( $ U $ is an open affine subset of $ X $, $ V $ an open affine subset of $ Y $) are
$$ \Gamma ( U, {\mathcal F} ) \otimes _ { k } \Gamma ( V, {\mathcal G} ). $$
More generally, let $ p: X \rightarrow S $ and $ q: Y \rightarrow S $ be morphisms (cf. Morphism) in the category of schemes, let $ h: X \times _ {S} Y \rightarrow S $ be their fibred product, and let $ {\mathcal F} $ and $ {\mathcal G} $ be quasi-coherent sheaves (cf. Quasi-coherent sheaf) of modules on $ X $ and $ Y $. Generalizing the construction of the sheaf $ {\mathcal F} \otimes _ {k} {\mathcal G} $, one can introduce sheaves of modules $ \mathop{\rm Tor} _ {m} ^ {S} ( {\mathcal F} , {\mathcal G} ) $ on $ X \times Y $ whose modules of sections for affine $ S $, $ X $ and $ Y $ are isomorphic to $ \mathop{\rm Tor} _ {m} ^ {A} ( \Gamma ( X, {\mathcal F} ), \Gamma ( Y, {\mathcal G} )) $, where $ A = \Gamma ( S, {\mathcal O} _ {S} ) $. Then [7] there exist two spectral sequences $ ( E ^ {r} ) $ and $ ( {} ^ \prime E ^ {r} ) $ with initial terms
$$ E _ {n, m } ^ {2} = \ R ^ {-} n h _ {*} ( \mathop{\rm Tor} _ {m} ^ {S} ( {\mathcal F} , {\mathcal G} )) $$
and
$$ E _ {n, m } ^ \prime 2 = \ \oplus _ {m _ {1} + m _ {2} = m } \mathop{\rm Tor} _ {n} ^ {S} ( R ^ {- m _ {1} } p _ {*} {\mathcal F} , R ^ {- m _ {2} } q _ {*} {\mathcal G} ), $$
having the same limit. The awkward formulation of the Künneth formula assumes a more familiar form in terms of derived functors [11]:
$$ Rp _ {*} ( {\mathcal F} ) \otimes _ { {\mathcal O} _ {S} } ^ { L } Rq _ {*} ( {\mathcal G} ) = \ Rh _ {*} \left ( {\mathcal F} \otimes _ { {\mathcal O} _ {S} } ^ { L } {\mathcal G} \right ) . $$
If the sheaves $ {\mathcal F} $ and $ {\mathcal G} $ are flat over $ S $, then the spectral sequence $ ( E ^ {r} ) $ is degenerate. Similarly, $ ( {} ^ \prime E ^ {r} ) $ degenerates if all $ R ^ {k} p _ {*} ( {\mathcal F} ) $( or all $ R ^ {k} q _ {*} ( {\mathcal G} ) $) are flat over $ S $. If both spectral sequences $ ( E ^ {r} ) $ and $ ( {} ^ \prime E ^ {r} ) $ are degenerate, the Künneth formula becomes
$$ R ^ {*} h _ {*} \left ( {\mathcal F} \otimes _ { {\mathcal O} _ {S} } {\mathcal G} \right ) \cong \ R ^ {*} p _ {*} ( {\mathcal F} ) \otimes _ { {\mathcal O} _ {S} } R ^ {*} q _ {k} ( {\mathcal G} ). $$
A Künneth formula is also valid for étale sheaves of $ A $- modules on schemes $ X $ and $ Y $, where $ A $ is a finite ring. It may be written as
$$ Rp _ {!} ( {\mathcal F} ) \otimes _ { A } ^ { L } Rq _ {!} ( {\mathcal G} ) = \ Rh _ {!} \left ( {\mathcal F} \otimes _ { A } ^ { L } {\mathcal G} \right ) , $$
where the $ ! $ means that the cohomology is taken with compact support. In particular (see [8]), if $ X $ and $ Y $ are complete algebraic varieties, the Künneth formula for the $ l $- adic cohomology is
$$ H ^ {*} ( X \times Y, \mathbf Q _ {l} ) = \ H ^ {*} ( X, \mathbf Q _ {l} ) \otimes _ {\mathbf Q _ {l} } H ^ {*} ( Y, \mathbf Q _ {l} ). $$
The formula has been proved for arbitrary varieties only on the assumption that the singularities can be resolved, e.g. for varieties over a field of characteristic zero.
There is also a version of the Künneth formula in $ K $- theory. Let $ X $ be a space such that the group $ K ^ {*} ( X) $ is finitely generated, and let $ Y $ be a cellular space. Then there is an exact sequence of $ \mathbf Z _ {2} $- graded modules
$$ 0 \rightarrow K ^ {*} ( X) \otimes K ^ {*} ( Y) \mathop \rightarrow \limits ^ \alpha K ^ {*} ( X \times Y) \mathop \rightarrow \limits ^ \beta $$
$$ \mathop \rightarrow \limits ^ \beta \mathop{\rm Tor} _ {1} ( K ^ {*} ( X), K ^ {*} ( Y)) \rightarrow 0, $$
where $ \alpha $ and $ \beta $ are homomorphisms of degree 0 and 1, respectively (see [5]). A particular case of this proposition is the Bott periodicity theorem for complex vector bundles. A Künneth formula is also known in bordism theory [10].
References
| [1a] | H. Künneth, "Ueber die Bettische Zahlen einer Produktmannigfaltigkeit" Math. Ann. , 90 (1923) pp. 65–85 |
| [1b] | H. Künneth, "Ueber die Torsionszahlen von Produktmannigfaltigkeiten" Math. Ann. , 91 (1924) pp. 125–134 |
| [2] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) MR0077480 Zbl 0075.24305 |
| [3] | A. Dold, "Lectures on algebraic topology" , Springer (1980) MR0606196 Zbl 0434.55001 |
| [4] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) MR0210112 MR1325242 Zbl 0145.43303 |
| [5] | M.F. Atiyah, "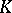 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [6] | L. Kaup, "Eine Künnethformel für Fréchetgarben" Math. Z. , 97 : 2 (1967) pp. 158–168 |
| [7] | A. Grothendieck, J. Dieudonné, "Eléments de géométrie algébrique" Publ. Math. IHES , 17 (1963) pp. Chapt. 3, Part 2 |
| [8] | M. Artin (ed.) A. Grothendieck (ed.) J.-L. Verdier (ed.) , Théorie des topos et cohomologie étale des schémas (SGA 4, vol. III) , Lect. notes in math. , 305 , Springer (1973) |
| [9] | J. Sampson, G. Washnitzer, "A Künneth formula for coherent algebraic sheaves" Illinois J. Math. , 3 : 3 (1959) pp. 389–402 |
| [10] | P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) MR0176478 Zbl 0125.40103 |
| [11] | R. Hartshorne, "Residues and duality" , Springer (1966) MR0222093 Zbl 0212.26101 |
Comments
More generally, cohomology theories have a Künneth formula spectral sequence for $ h ^ {*} ( X \times Y) $, where $ X $ and $ Y $ are as in the last section of the main article above (e.g., for equivariant $ K $- theory see [a1]).
References
| [a1] | L. Hodgkin, "The equivariant Künneth theorem in $K$-theory" , Lect. notes in math. , 496 , Springer (1975) |
Künneth formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K%C3%BCnneth_formula&oldid=55899