Difference between revisions of "Dendritic manifold"
m (OldImage template added) |
|||
| Line 133: | Line 133: | ||
realizes a quadratic form of order eight, in which every element on the main diagonal equals 2, while the signature equals 8. | realizes a quadratic form of order eight, in which every element on the main diagonal equals 2, while the signature equals 8. | ||
| − | In constructing the Kervaire manifolds $ K ^ {4k+} | + | In constructing the Kervaire manifolds $ K ^ {4k+ 2} $ |
| − | one takes two copies of the block obtained as the tubular neighbourhood $ E ^ {4k+} | + | one takes two copies of the block obtained as the tubular neighbourhood $ E ^ {4k+ 2} $ |
| − | of the diagonal in the product $ S ^ {2k+} | + | of the diagonal in the product $ S ^ {2k+ 1} \times S ^ {2k+ 1} $. |
They are glued together so that the intersection matrix has the form | They are glued together so that the intersection matrix has the form | ||
| Line 148: | Line 148: | ||
The boundary of a Milnor manifold $ \partial M ^ {4k} $( | The boundary of a Milnor manifold $ \partial M ^ {4k} $( | ||
| − | a Milnor sphere) is never diffeomorphic to the standard sphere $ S ^ {4k-} | + | a Milnor sphere) is never diffeomorphic to the standard sphere $ S ^ {4k- 1} $. |
As regards Kervaire manifolds, this problem has not yet (1987) been conclusively solved. If $ 2k + 1 \neq 2 ^ {i} - 1 $, | As regards Kervaire manifolds, this problem has not yet (1987) been conclusively solved. If $ 2k + 1 \neq 2 ^ {i} - 1 $, | ||
then the boundary of a Kervaire manifold $ \partial K ^ {4k+} 2 $( | then the boundary of a Kervaire manifold $ \partial K ^ {4k+} 2 $( | ||
| Line 157: | Line 157: | ||
it remains unsolved (cf. [[Kervaire invariant|Kervaire invariant]]). | it remains unsolved (cf. [[Kervaire invariant|Kervaire invariant]]). | ||
| − | The Kervaire manifolds $ K ^ {4k+} | + | The Kervaire manifolds $ K ^ {4k+ 2 }$ |
| − | of dimension 2, 6 or 14 are products of spheres $ S ^ {2k+} | + | of dimension 2, 6 or 14 are products of spheres $ S ^ {2k+ 1} \times S ^ {2k+ 1} $, |
$ k = 0 , 1 , 3 $ | $ k = 0 , 1 , 3 $ | ||
respectively, after an open cell has been discarded, while all other Kervaire manifolds are not homeomorphic to the products of spheres with a discarded cell. | respectively, after an open cell has been discarded, while all other Kervaire manifolds are not homeomorphic to the products of spheres with a discarded cell. | ||
| Line 165: | Line 165: | ||
and $ {\widehat{K} } {} ^ {4k} $ | and $ {\widehat{K} } {} ^ {4k} $ | ||
are often used in the topology of manifolds. These manifolds are obtained by adding a cone over the boundary of, respectively, the Milnor manifolds $ M ^ {4k} $ | are often used in the topology of manifolds. These manifolds are obtained by adding a cone over the boundary of, respectively, the Milnor manifolds $ M ^ {4k} $ | ||
| − | and the Kervaire manifolds $ K ^ {4k+} | + | and the Kervaire manifolds $ K ^ {4k+2 }$. |
| − | In the theory of four-dimensional manifolds a certain simply-connected almost-parallelizable manifold | + | In the theory of four-dimensional manifolds a certain simply-connected almost-parallelizable manifold $W^{4}$ (usually called a Rokhlin manifold) plays an especially important role; its signature is 16, cf. [[#References|[6]]]. In the known examples of Rokhlin manifolds, the minimum value of the two-dimensional [[Betti number|Betti number]] is 22. The second manifold is $ W ^ {4} ( \Gamma ) $, |
| − | usually called a Rokhlin manifold) plays an especially important role; its signature is 16, cf. [[#References|[6]]]. In the known examples of Rokhlin manifolds, the minimum value of the two-dimensional [[Betti number|Betti number]] is 22. The second manifold is $ W ^ {4} ( \Gamma ) $, | ||
where $ \Gamma $ | where $ \Gamma $ | ||
is the graph indicated above, and the tubular neighbourhood of the diagonal in the product $ S ^ {2} \times S ^ {2} $ | is the graph indicated above, and the tubular neighbourhood of the diagonal in the product $ S ^ {2} \times S ^ {2} $ | ||
| Line 174: | Line 173: | ||
The three-dimensional dendritic manifolds $ M ^ {3} = \partial W ^ {4} ( T) $ | The three-dimensional dendritic manifolds $ M ^ {3} = \partial W ^ {4} ( T) $ | ||
| − | belong to the class of so-called Seifert manifolds. Not all three-dimensional manifolds are dendritic manifolds; the [[ | + | belong to the class of so-called Seifert manifolds. Not all three-dimensional manifolds are dendritic manifolds; the [[Poincaré conjecture]] holds for dendritic manifolds. In particular, three-dimensional lens spaces (cf. [[Lens space]]) are obtained by glueing two blocks only. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Kervaire, "A manifold which does not admit any differentiable structure" ''Comment. Math. Helv.'' , '''34''' (1960) pp. 257–270 {{MR|139172}} {{ZBL|0145.20304}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Kervaire, J. Milnor, "Groups of homotopy spheres. I" ''Ann. of Math.'' , '''77''' : 3 (1963) pp. 504–537 {{MR|0148075}} {{ZBL|0115.40505}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.W. Milnor, "Differential topology" , ''Lectures on modern mathematics'' , '''II''' , Wiley (1964) pp. 165–183 {{MR|0178474}} {{ZBL|0142.40803}} {{ZBL|0123.16201}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Hirzebruch, W.D. Neumann, S.S. Koh, "Differentiable manifolds and quadratic forms" , M. Dekker (1971) {{MR|0341499}} {{ZBL|0226.57001}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972) {{MR|0358813}} {{ZBL|0239.57016}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R. Mandelbaum, "Four-dimensional topology: an introduction" ''Bull. Amer. Math. Soc.'' , '''2''' : 1 (1980) pp. 1–159 {{MR|0551752}} {{ZBL|0476.57005}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> M. Kervaire, "A manifold which does not admit any differentiable structure" ''Comment. Math. Helv.'' , '''34''' (1960) pp. 257–270 {{MR|139172}} {{ZBL|0145.20304}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Kervaire, J. Milnor, "Groups of homotopy spheres. I" ''Ann. of Math.'' , '''77''' : 3 (1963) pp. 504–537 {{MR|0148075}} {{ZBL|0115.40505}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.W. Milnor, "Differential topology" , ''Lectures on modern mathematics'' , '''II''' , Wiley (1964) pp. 165–183 {{MR|0178474}} {{ZBL|0142.40803}} {{ZBL|0123.16201}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> F. Hirzebruch, W.D. Neumann, S.S. Koh, "Differentiable manifolds and quadratic forms" , M. Dekker (1971) {{MR|0341499}} {{ZBL|0226.57001}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972) {{MR|0358813}} {{ZBL|0239.57016}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R. Mandelbaum, "Four-dimensional topology: an introduction" ''Bull. Amer. Math. Soc.'' , '''2''' : 1 (1980) pp. 1–159 {{MR|0551752}} {{ZBL|0476.57005}} </TD></TR></table> | ||
====Comments==== | ====Comments==== | ||
| − | The technique described in the article above and leading to so-called "dendritic manifolds" (a phrase not often used in the West) is known as [[ | + | The technique described in the article above and leading to so-called "dendritic manifolds" (a phrase not often used in the West) is known as [[surgery]], plumbing or as the technique of spherical modification. |
{{OldImage}} | {{OldImage}} | ||
Revision as of 12:22, 10 April 2023
A smooth odd-dimensional manifold of a special type which is the boundary of an even-dimensional manifold constructed from fibrations over spheres by a glueing scheme specified by some graph (tree).
Let $ p _ {i} : E _ {i} ^ {2n} \rightarrow S _ {i} ^ {n} $, $ i = 1, 2 \dots $ be a fibration over $ n $- spheres with as fibre the $ n $- ball $ D ^ {n} $ and as structure group the group $ \mathop{\rm SO} _ {n} $, and let $ B _ {i} ^ {n} $ be the closed standard $ n $- ball in the $ n $- sphere $ S _ {i} ^ {n} $; then
$$ p _ {i} ^ {-} 1 ( B _ {i} ^ {n} ) \approx B _ {i} ^ {n} \times D _ {i} ^ {n} , $$
where $ D _ {i} ^ {n} $ is the fibre $ p _ {i} $. Let
$$ \gamma _ {ij} : B _ {i} ^ {n} \times D _ {i} ^ {n} \rightarrow B _ {j} ^ {n} \times D _ {j} ^ {n} ,\ i = 1, 2 , $$
be a homeomorphism realizing the glueing of two fibrations $ p _ {i} $, $ p _ {j} $ and mapping each $ n $- ball $ B ^ {n} \times x $ from $ B _ {i} ^ {n} \times D _ {i} ^ {n} $ into some ball $ y \times D ^ {n} $ from $ B _ {j} ^ {n} \times D _ {j} ^ {n} $( the glueing alters the factors of the direct product $ B ^ {n} \times D ^ {n} $). The result of glueing two fibrations $ p _ {i} $, $ p _ {j} $ is the $ 2n $- dimensional manifold $ E _ {i} ^ {2n} \cup _ {\gamma _ {ij} } E _ {j} ^ {2n} $ which, as a result of "angle smoothing" , is converted to a smooth manifold.
The fibrations $ E _ {i} ^ {2n} $ are considered as "structural blocks" from which it is possible to construct, by pairwise glueing, the resulting smooth manifold as follows. Let $ T $ be a one-dimensional finite complex (a graph). Each vertex of $ T $ is brought into correspondence with a block $ E _ {i} ^ {2n} $; next, $ k $, $ k = 1 , 2 \dots $ non-intersecting $ n $- balls $ B _ {i _ {k} } ^ {k} $ are selected in $ S _ {i} ^ {n} $, where $ k $ is equal to the branching index of the respective vertex, and the glueing is performed according to the scheme indicated by $ T $. The manifold with boundary thus obtained is denoted by $ W ^ {2n} ( T ) $( neglecting the dependence on the choice of $ E _ {i} ^ {2n} $). If $ T $ is a tree, and therefore the graph is without cycles, the boundary $ \partial W ^ {2n} ( T ) = M ^ {2n-} 1 $ is said to be a dendritic manifold.
If $ T $ is a tree, $ W ^ {2n} ( T ) $ has the homotopy type of a bouquet of $ k $ spheres, where $ k $ is the number of vertices of $ T $.
The dendritic manifold $ M ^ {2n-} 1 = \partial W ^ {2n} ( T ) $ is an integral homology $ ( 2n - 1 ) $- sphere if and only if the determinant of the matrix of the integral bilinear intersection $ ( - 1 ) ^ {n} $- form defined on the lattice of $ n $- dimensional homology groups $ H _ {n} ( W ^ {2n} , \mathbf Z ) $ equals $ \pm 1 $. If this condition is met, the manifold $ W ^ {2n} ( T ) $ is called a plumbing.
If $ T $ is a tree and $ n \geq 3 $, $ \partial W ^ {2n} ( T ) $ is simply connected; if $ W ^ {2n} $ is a plumbing, the boundary $ \partial W ^ {2n} $ is a homotopy sphere if $ n \geq 3 $.
If the plumbing $ W ^ {4k} $ is parallelizable, the diagonal of the intersection matrix of $ 2k $- dimensional cycles is occupied by even numbers; in such a case the signature of the intersection matrix is divisible by 8. The plumbing $ W ^ {4k} $ is parallelizable if and only if all the fibrations over $ S ^ {2k} $ used in constructing $ W ^ {4k} $ are stably trivial; e.g., if all fibrations used in constructing $ W ^ {4k} $ are tangent bundles on discs over $ 2k $- dimensional spheres, the plumbing $ W ^ {4k} $ is parallelizable. The plumbing $ W ^ {4k+} 2 $ will be parallelizable if and only if any fibration $ E _ {i} ^ {4k+} 2 $ used as a block in the construction of $ W ^ {4k+} 2 $ is either trivial or is a tubular neighbourhood of the diagonal in the product $ S ^ {2k+} 1 \times S ^ {2k+} 1 $, i.e. is a tangent bundle on discs over $ S ^ {2k+} 1 $. If the plumbing $ W ^ {4k+} 2 $ is parallelizable, its intersection matrix can be reduced to the symplectic form consisting of blocks
$$ \left \| \begin{array}{rr} 0 & 1 \\ - 1 & 0 \\ \end{array} \right \| $$
situated along the main diagonal.
Especially important plumbings are the Milnor manifolds of dimension $ 4k $, $ k > 1 $, and the Kervaire manifolds of dimension $ 4k + 2 $, $ k \geq 0 $. The Milnor manifolds are constructed as follows: A few copies of the tubular neighbourhood $ E ^ {4k} $ of the diagonal in the product $ S ^ {2k} \times S ^ {2k} $ are taken as blocks, while the graph $ T $ is of the form
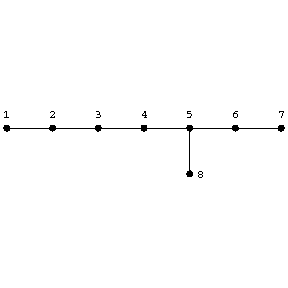
Figure: d031010a
Under these conditions the manifold $ W ^ {4k} ( T ) $ realizes a quadratic form of order eight, in which every element on the main diagonal equals 2, while the signature equals 8.
In constructing the Kervaire manifolds $ K ^ {4k+ 2} $ one takes two copies of the block obtained as the tubular neighbourhood $ E ^ {4k+ 2} $ of the diagonal in the product $ S ^ {2k+ 1} \times S ^ {2k+ 1} $. They are glued together so that the intersection matrix has the form
$$ \left \| \begin{array}{rr} 0 & 1 \\ - 1 & 0 \\ \end{array} \right \| . $$
The boundary of a Milnor manifold $ \partial M ^ {4k} $( a Milnor sphere) is never diffeomorphic to the standard sphere $ S ^ {4k- 1} $. As regards Kervaire manifolds, this problem has not yet (1987) been conclusively solved. If $ 2k + 1 \neq 2 ^ {i} - 1 $, then the boundary of a Kervaire manifold $ \partial K ^ {4k+} 2 $( a Kervaire sphere) is always non-standard; if $ 2k + 1 = 2 ^ {i} - 1 $, one obtains the standard sphere $ S ^ {4k+} 1 $ for $ 1 \leq i \leq 6 $, while for other $ i $ it remains unsolved (cf. Kervaire invariant).
The Kervaire manifolds $ K ^ {4k+ 2 }$ of dimension 2, 6 or 14 are products of spheres $ S ^ {2k+ 1} \times S ^ {2k+ 1} $, $ k = 0 , 1 , 3 $ respectively, after an open cell has been discarded, while all other Kervaire manifolds are not homeomorphic to the products of spheres with a discarded cell.
The PL-manifolds $ {\widehat{M} } {} ^ {4k} $ and $ {\widehat{K} } {} ^ {4k} $ are often used in the topology of manifolds. These manifolds are obtained by adding a cone over the boundary of, respectively, the Milnor manifolds $ M ^ {4k} $ and the Kervaire manifolds $ K ^ {4k+2 }$. In the theory of four-dimensional manifolds a certain simply-connected almost-parallelizable manifold $W^{4}$ (usually called a Rokhlin manifold) plays an especially important role; its signature is 16, cf. [6]. In the known examples of Rokhlin manifolds, the minimum value of the two-dimensional Betti number is 22. The second manifold is $ W ^ {4} ( \Gamma ) $, where $ \Gamma $ is the graph indicated above, and the tubular neighbourhood of the diagonal in the product $ S ^ {2} \times S ^ {2} $ is taken as the block. The boundary of the manifold $ Q ^ {3} = \partial W ^ {4} ( \Gamma ) $ thus obtained is a dodecahedral space which is not simply connected.
The three-dimensional dendritic manifolds $ M ^ {3} = \partial W ^ {4} ( T) $ belong to the class of so-called Seifert manifolds. Not all three-dimensional manifolds are dendritic manifolds; the Poincaré conjecture holds for dendritic manifolds. In particular, three-dimensional lens spaces (cf. Lens space) are obtained by glueing two blocks only.
References
| [1] | M. Kervaire, "A manifold which does not admit any differentiable structure" Comment. Math. Helv. , 34 (1960) pp. 257–270 MR139172 Zbl 0145.20304 |
| [2] | M. Kervaire, J. Milnor, "Groups of homotopy spheres. I" Ann. of Math. , 77 : 3 (1963) pp. 504–537 MR0148075 Zbl 0115.40505 |
| [3] | J.W. Milnor, "Differential topology" , Lectures on modern mathematics , II , Wiley (1964) pp. 165–183 MR0178474 Zbl 0142.40803 Zbl 0123.16201 |
| [4] | F. Hirzebruch, W.D. Neumann, S.S. Koh, "Differentiable manifolds and quadratic forms" , M. Dekker (1971) MR0341499 Zbl 0226.57001 |
| [5] | W.B. Browder, "Surgery on simply-connected manifolds" , Springer (1972) MR0358813 Zbl 0239.57016 |
| [6] | R. Mandelbaum, "Four-dimensional topology: an introduction" Bull. Amer. Math. Soc. , 2 : 1 (1980) pp. 1–159 MR0551752 Zbl 0476.57005 |
Comments
The technique described in the article above and leading to so-called "dendritic manifolds" (a phrase not often used in the West) is known as surgery, plumbing or as the technique of spherical modification.
Dendritic manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dendritic_manifold&oldid=53418