Difference between revisions of "Modular form"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 47870 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
''of one complex variable, elliptic modular form'' | ''of one complex variable, elliptic modular form'' | ||
| − | A function | + | A function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644201.png" /> on the upper half-plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644202.png" /> satisfying for some fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644203.png" /> the automorphicity condition |
| − | on the upper half-plane | ||
| − | satisfying for some fixed | ||
| − | the automorphicity condition | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644204.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
for any element | for any element | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644205.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644206.png" /> is the group of integer-valued matrices with determinant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644207.png" />), and such that | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644208.png" /></td> </tr></table> | |
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m0644209.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442011.png" />. The integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442012.png" /> is called the weight of the modular form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442013.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442014.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442015.png" /> is called a parabolic modular form. There is also [[#References|[8]]] a definition of modular forms for all real values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442016.png" />. | |
| − | + | An example of a modular form of weight <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442017.png" /> is given by the Eisenstein series (see [[#References|[4]]]) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442018.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | where the asterisk means that the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442019.png" /> is excluded from summation. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442020.png" /> for odd <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442021.png" /> and | |
| − | is | ||
| − | |||
| − | |||
| − | |||
| − | and | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442022.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442024.png" /> is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442025.png" />-th Bernoulli number (cf. [[Bernoulli numbers|Bernoulli numbers]]). | |
| − | |||
| − | |||
| − | + | The set of modular forms of weight <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442026.png" /> is a complex vector space, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442027.png" />; in this connection, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442028.png" />. The direct sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442029.png" /> forms a [[Graded algebra|graded algebra]] isomorphic to the ring of polynomials in the independent variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442031.png" /> (see [[#References|[3]]]). | |
| − | |||
| − | The [[ | ||
| − | + | For each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442032.png" /> the [[Complex torus|complex torus]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442033.png" /> is analytically isomorphic to the [[Elliptic curve|elliptic curve]] given by the equation | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442034.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | ( | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442036.png" />. The [[Discriminant|discriminant]] of the cubic polynomial on the right-hand side of (2) is a parabolic modular form of weight 12: |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442037.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442038.png" /> is the [[Ramanujan function|Ramanujan function]] (see [[#References|[1]]]). | |
| − | + | For each integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442039.png" /> modular forms of higher level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442040.png" /> have been introduced, satisfying (1) only for elements | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442041.png" /></td> </tr></table> | |
| − | |||
| − | + | of a congruence subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442042.png" /> of level <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442043.png" /> of the modular group. In this case, related to the modular form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442044.png" /> is the holomorphic differential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442045.png" /> on the modular curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442046.png" />. A well-known example of a modular form of higher level is the [[Theta-series|theta-series]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442047.png" /> associated to an integer-valued positive-definite quadratic form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442048.png" />: | |
| − | modular | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442049.png" /></td> </tr></table> | |
| − | |||
| − | + | which is a modular form of higher level and of weight <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442050.png" />. In this example <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442051.png" /> is the integer equal to the number of solutions of the Diophantine equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442052.png" />. | |
| − | of level | ||
| − | of | ||
| − | is the | ||
| − | |||
| − | |||
| − | |||
| − | + | The theory of modular forms allows one to obtain an estimate, and sometimes a precise formula, for numbers of the type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442053.png" /> (and congruences, such as the Ramanujan congruence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442054.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442055.png" />)), and also to investigate their divisibility properties (see [[#References|[7]]]). Best estimates for numbers of the type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442056.png" /> have been obtained (see [[#References|[2]]]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The theory of modular forms allows one to obtain an estimate, and sometimes a precise formula, for numbers of the type | ||
| − | and congruences, such as the Ramanujan congruence | ||
| − | |||
| − | and also to investigate their divisibility properties (see [[#References|[7]]]). Best estimates for numbers of the type | ||
| − | have been obtained (see [[#References|[2]]]). | ||
Important arithmetic applications of modular forms are related to the [[Dirichlet series]] | Important arithmetic applications of modular forms are related to the [[Dirichlet series]] | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442057.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | i.e. the [[Mellin transform|Mellin transform]] of | + | i.e. the [[Mellin transform|Mellin transform]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442058.png" />. Such Dirichlet series have been the subject of detailed study (estimates of coefficients, analyticity properties, the functional equation, Euler product expansion) in view of the presence of a non-trivial ring of correspondences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442059.png" /> on a modular curve. For a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442060.png" /> this ring is generated by the correspondence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442061.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442062.png" /> runs through the set of all representatives of the elements of the quotient set |
| − | Such Dirichlet series have been the subject of detailed study (estimates of coefficients, analyticity properties, the functional equation, Euler product expansion) in view of the presence of a non-trivial ring of correspondences | ||
| − | on a modular curve. For a curve | ||
| − | this ring is generated by the correspondence | ||
| − | where | ||
| − | runs through the set of all representatives of the elements of the quotient set | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064420/m06442063.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | . | ||
| − | |||
The correspondences induce linear operators (Hecke operators) acting on the space of modular forms. They are self-adjoint relative to the Peterson scalar product (see [[#References|[3]]], [[#References|[7]]]). Modular forms which are eigen functions of the Hecke operators are characterized by the fact that their Mellin transforms have Euler product expansions. | The correspondences induce linear operators (Hecke operators) acting on the space of modular forms. They are self-adjoint relative to the Peterson scalar product (see [[#References|[3]]], [[#References|[7]]]). Modular forms which are eigen functions of the Hecke operators are characterized by the fact that their Mellin transforms have Euler product expansions. | ||
| Line 184: | Line 63: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , '''1''' , Springer (1964) pp. Chapt.8</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–307</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Introduction to modular forms" , Springer (1976)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> O.M. Fenko, "Applications of the theory of modular forms to number theory" ''J. Soviet Math.'' , '''14''' : 4 (1977) pp. 1307–1362 ''Itogi Nauk. i Tekhn. Algebra Topol. Geom.'' , '''15''' (1977) pp. 5–91</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 1–6'' , ''Lect. notes in math.'' , '''320; 349; 350; 476; 601; 627''' , Springer (1973–1977)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A. Ogg, "Modular forms and Dirichlet series" , Benjamin (1969)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , '''1''' , Springer (1964) pp. Chapt.8</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–307</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Introduction to modular forms" , Springer (1976)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> O.M. Fenko, "Applications of the theory of modular forms to number theory" ''J. Soviet Math.'' , '''14''' : 4 (1977) pp. 1307–1362 ''Itogi Nauk. i Tekhn. Algebra Topol. Geom.'' , '''15''' (1977) pp. 5–91</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , ''Modular functions of one variable. 1–6'' , ''Lect. notes in math.'' , '''320; 349; 350; 476; 601; 627''' , Springer (1973–1977)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A. Ogg, "Modular forms and Dirichlet series" , Benjamin (1969)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
A parabolic modular form is also called a cusp form. | A parabolic modular form is also called a cusp form. | ||
Revision as of 13:51, 7 June 2020
of one complex variable, elliptic modular form
A function 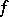 on the upper half-plane
on the upper half-plane  satisfying for some fixed
satisfying for some fixed 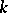 the automorphicity condition
the automorphicity condition
 | (1) |
for any element
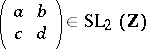 |
(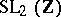 is the group of integer-valued matrices with determinant
is the group of integer-valued matrices with determinant 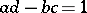 ), and such that
), and such that
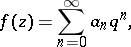 |
where 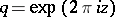 ,
, 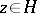 ,
, 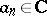 . The integer
. The integer 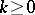 is called the weight of the modular form
is called the weight of the modular form 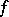 . If
. If 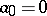 , then
, then 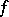 is called a parabolic modular form. There is also [8] a definition of modular forms for all real values of
is called a parabolic modular form. There is also [8] a definition of modular forms for all real values of 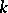 .
.
An example of a modular form of weight 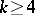 is given by the Eisenstein series (see [4])
is given by the Eisenstein series (see [4])
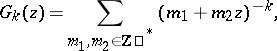 |
where the asterisk means that the pair 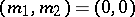 is excluded from summation. Here
is excluded from summation. Here 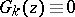 for odd
for odd 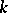 and
and
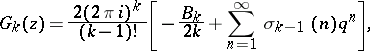 |
where 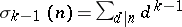 and
and 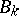 is the
is the 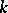 -th Bernoulli number (cf. Bernoulli numbers).
-th Bernoulli number (cf. Bernoulli numbers).
The set of modular forms of weight 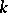 is a complex vector space, denoted by
is a complex vector space, denoted by 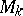 ; in this connection,
; in this connection, 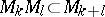 . The direct sum
. The direct sum 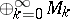 forms a graded algebra isomorphic to the ring of polynomials in the independent variables
forms a graded algebra isomorphic to the ring of polynomials in the independent variables  and
and 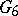 (see [3]).
(see [3]).
For each 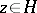 the complex torus
the complex torus 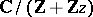 is analytically isomorphic to the elliptic curve given by the equation
is analytically isomorphic to the elliptic curve given by the equation
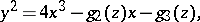 | (2) |
where 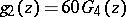 ,
, 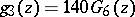 . The discriminant of the cubic polynomial on the right-hand side of (2) is a parabolic modular form of weight 12:
. The discriminant of the cubic polynomial on the right-hand side of (2) is a parabolic modular form of weight 12:
 |
where 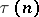 is the Ramanujan function (see [1]).
is the Ramanujan function (see [1]).
For each integer  modular forms of higher level
modular forms of higher level 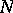 have been introduced, satisfying (1) only for elements
have been introduced, satisfying (1) only for elements
 |
of a congruence subgroup 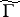 of level
of level 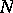 of the modular group. In this case, related to the modular form
of the modular group. In this case, related to the modular form 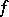 is the holomorphic differential
is the holomorphic differential 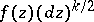 on the modular curve
on the modular curve 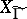 . A well-known example of a modular form of higher level is the theta-series
. A well-known example of a modular form of higher level is the theta-series 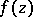 associated to an integer-valued positive-definite quadratic form
associated to an integer-valued positive-definite quadratic form 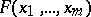 :
:
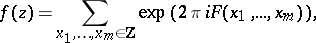 |
which is a modular form of higher level and of weight 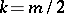 . In this example
. In this example 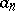 is the integer equal to the number of solutions of the Diophantine equation
is the integer equal to the number of solutions of the Diophantine equation 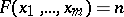 .
.
The theory of modular forms allows one to obtain an estimate, and sometimes a precise formula, for numbers of the type 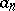 (and congruences, such as the Ramanujan congruence
(and congruences, such as the Ramanujan congruence 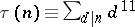 (
( )), and also to investigate their divisibility properties (see [7]). Best estimates for numbers of the type
)), and also to investigate their divisibility properties (see [7]). Best estimates for numbers of the type 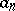 have been obtained (see [2]).
have been obtained (see [2]).
Important arithmetic applications of modular forms are related to the Dirichlet series
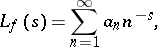 |
i.e. the Mellin transform of 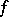 . Such Dirichlet series have been the subject of detailed study (estimates of coefficients, analyticity properties, the functional equation, Euler product expansion) in view of the presence of a non-trivial ring of correspondences
. Such Dirichlet series have been the subject of detailed study (estimates of coefficients, analyticity properties, the functional equation, Euler product expansion) in view of the presence of a non-trivial ring of correspondences 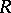 on a modular curve. For a curve
on a modular curve. For a curve 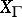 this ring is generated by the correspondence
this ring is generated by the correspondence 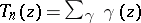 , where
, where 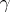 runs through the set of all representatives of the elements of the quotient set
runs through the set of all representatives of the elements of the quotient set
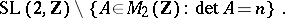 |
The correspondences induce linear operators (Hecke operators) acting on the space of modular forms. They are self-adjoint relative to the Peterson scalar product (see [3], [7]). Modular forms which are eigen functions of the Hecke operators are characterized by the fact that their Mellin transforms have Euler product expansions.
Another direction in the theory of modular forms is related to the study of modular curves and the associated fibrations, the Kuga varieties (cf. Modular curve), and also to the theory of infinite-dimensional representations of algebraic adèle groups. Here the theory of modular forms of one variable was successfully transferred to the case of several variables (see [6]). A survey of the number-theoretic applications of modular forms is given in [5].
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1964) pp. Chapt.8 |
| [2] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–307 |
| [3] | S. Lang, "Introduction to modular forms" , Springer (1976) |
| [4] | J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French) |
| [5] | O.M. Fenko, "Applications of the theory of modular forms to number theory" J. Soviet Math. , 14 : 4 (1977) pp. 1307–1362 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 15 (1977) pp. 5–91 |
| [6] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 1–6 , Lect. notes in math. , 320; 349; 350; 476; 601; 627 , Springer (1973–1977) |
| [7] | A. Ogg, "Modular forms and Dirichlet series" , Benjamin (1969) |
| [8] | R.A. Rankin, "Modular forms and functions" , Cambridge Univ. Press (1977) |
Comments
A parabolic modular form is also called a cusp form.
Modular form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modular_form&oldid=47870