Difference between revisions of "Plane real algebraic curve"
m (Texed) |
m (fixed) |
||
| Line 3: | Line 3: | ||
[[Affine space|Affine space]]) whose coordinates satisfy | [[Affine space|Affine space]]) whose coordinates satisfy | ||
| − | $$f(x, y)=0 | + | $$\begin{equation} f(x, y)=0 \end{equation}$$ |
where $f(x, y)$ is a | where $f(x, y)$ is a | ||
[[Polynomial|polynomial]] of degree $n$ in the coordinates $x$ and $y$; the number $n$ is called the order of the curve $L$. If $f$ is a reducible polynomial, i.e. if it splits into factors $f_1, \ldots, f_k$, then the curve $L$ defined by (1) is called reducible and is the union of the curves $L_1, \ldots, L_k$ (the components of $L$) defined, correspondingly, by the equations | [[Polynomial|polynomial]] of degree $n$ in the coordinates $x$ and $y$; the number $n$ is called the order of the curve $L$. If $f$ is a reducible polynomial, i.e. if it splits into factors $f_1, \ldots, f_k$, then the curve $L$ defined by (1) is called reducible and is the union of the curves $L_1, \ldots, L_k$ (the components of $L$) defined, correspondingly, by the equations | ||
| Line 25: | Line 25: | ||
$$ | $$ | ||
| + | \begin{equation} | ||
u = \frac{\frac{\partial f}{\partial x}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, \qquad | u = \frac{\frac{\partial f}{\partial x}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, \qquad | ||
| − | + | v = \frac{\frac{\partial f}{\partial y}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, | |
| + | \end{equation} | ||
$$ | $$ | ||
where $f$ is a polynomial defining $L$. The equation | where $f$ is a polynomial defining $L$. The equation | ||
| Line 51: | Line 53: | ||
A non-singular point $x$ on the plane real algebraic curve $L$ defined by (1) is called a point of inflection if at $x$, | A non-singular point $x$ on the plane real algebraic curve $L$ defined by (1) is called a point of inflection if at $x$, | ||
| − | $$H(x, y) = \begin{vmatrix} | + | $$ |
| + | \begin{equation} | ||
| + | H(x, y) = \begin{vmatrix} | ||
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x\partial y} & \frac{\partial f}{\partial x} \\ | \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x\partial y} & \frac{\partial f}{\partial x} \\ | ||
\frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial f}{\partial y} \\ | \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial f}{\partial y} \\ | ||
\frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & 0 | \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & 0 | ||
\end{vmatrix} = 0. | \end{vmatrix} = 0. | ||
| + | \end{equation} | ||
$$ | $$ | ||
In other words, points of inflection are points at which $L$ intersects the curve $H$ defined by (3); $H$ is called the Hessian of $L$. The points of inflection on a curve $L$ correspond to points of return on the dual curve $L^*$. | In other words, points of inflection are points at which $L$ intersects the curve $H$ defined by (3); $H$ is called the Hessian of $L$. The points of inflection on a curve $L$ correspond to points of return on the dual curve $L^*$. | ||
Latest revision as of 00:44, 12 August 2019
A set of points $L$ in the real affine plane (cf. Affine space) whose coordinates satisfy
$$\begin{equation} f(x, y)=0 \end{equation}$$ where $f(x, y)$ is a polynomial of degree $n$ in the coordinates $x$ and $y$; the number $n$ is called the order of the curve $L$. If $f$ is a reducible polynomial, i.e. if it splits into factors $f_1, \ldots, f_k$, then the curve $L$ defined by (1) is called reducible and is the union of the curves $L_1, \ldots, L_k$ (the components of $L$) defined, correspondingly, by the equations
$$f_1 = 0, \ldots, f_k = 0.$$ If on the other hand $f$ is an irreducible polynomial, $L$ is called an irreducible curve. Two irreducible plane real algebraic curves, one of order $n$ and the other of order $m$, intersect in at most $mn$ points (Bezout's theorem).
A given plane real algebraic curve $L$ can be defined by different equations. Let $I_L$ be the set of polynomials that vanish at all points of $L$. If $L$ is irreducible, then $fg=0$ on $L$ implies that $f$ or $g$ is zero; in that case the quotient ring $K_L = K/I_L$ does not have divisors of zero (cf. Zero divisor) and is called the ring of polynomials on $L$ (here $K$ is the ring of all polynomials).
With an irreducible plane real algebraic curve $L$ one associates also a certain field $K(L)$, called the field of rational functions on $L$. It consists of the rational functions $p(x, y)/q(x, y)$, where $q$ is not divisible by $f$, considered up to equality on $L$ ($p/q$ and $\tilde p/\tilde q$ are called equal on the curve $L$ defined by (1) if the polynomial $p\tilde q - \tilde p q$ is divisible by $f$). The field $K(L)$ is the field of fractions of $K_L$ (cf. Fractions, ring of).
A mapping $F:(x, y) \to (\phi(x, y), \psi(x, y))$ of the plane into itself is called regular on the plane real algebraic curve $L$ if $\phi, \psi \in K(L)$. Curves $L$ and $M$ are called isomorphic if there are regular mappings (correspondingly, on $L$ and $M$) $F:L\to M$ and $G:M\to L$ that are mutually inverse; then the rings $K(L)$ and $K(M)$ are isomorphic. In particular, affinely-equivalent curves are isomorphic.
More generally, a rational mapping from a curve $L$ to a curve $M$ is represented by rational functions. It establishes a correspondence between all points on the curves apart from a finite number of them and is defined as follows. Let $f=0$ and $g=0$ be equations of $L$ and $M$, respectively; then a rational mapping $F$ is defined by a pair of rational functions $\phi$ and $\psi$ defined on $L$ and such that $g(\phi, \psi)=0$ on $M$. Two curves $L$ and $M$ are called birationally equivalent if there exist rational mappings from $L$ to $M$ and from $M$ to $L$ that are inverse to each other; here the fields $K(L)$ and $K(M)$ are isomorphic. Such rational mappings are called birational, or Cremona, transformations. All Cremona transformations on the plane are realized by the successive execution of the standard quadratic transformation $x\to 1/x$, $y \to 1/y$ and projective transformations. Birational equivalence is a coarser relation than isomorphism, but the classification of plane real algebraic curves from this point of view is simpler and easier to survey.
A very simple example of a rational mapping is a projective transformation. An important part is played by the dual mapping of an irreducible curve $L$ distinct from a straight line into the curve $L^*$ dual to $L$, defined by the formulas:
$$ \begin{equation} u = \frac{\frac{\partial f}{\partial x}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, \qquad v = \frac{\frac{\partial f}{\partial y}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, \end{equation} $$ where $f$ is a polynomial defining $L$. The equation
$$g(u, v)=0$$ defining $L^*$, is obtained by eliminating $x$ and $y$ from (1) and (2). The relationship between the dual mapping and the tangential transformation means that the curve $L^*$ itself in some cases can be represented as the envelope of the family of straight lines tangent to $L$.
The order of $L^*$ is called the class $n^*$ of the curve $L$. The duality relation is reciprocal, i.e. $L^{**} = L$, and it is a reflection of the duality principle in projective geometry.
A point $x$ on the plane real algebraic curve $L$ defined by (1) is called a singular point if $\text{grad } f = 0$ at $x$. The analysis of singularities is a necessary element in the investigation of $L$, but a complete classification of singularities is at present far from being complete (1990).
If all the derivatives of the polynomial $f$ up to and including order $r-1$ vanish at a point $x$, while the derivative of order $r$ differs from zero at $x$, then $x$ is called a point of multiplicity $r$, and it is called an ordinary point of multiplicity $r$ if there exist $r$ different tangents there. Examples of singular points are:
1) $x^3-x^2+y^2=0$; $(0,0)$ is an ordinary double point, a point of self-intersection;
2) $x^2+x^3+y^2=0$; $(0, 0)$ is an isolated point;
3) $x^3+y^2=0$; $(0,0)$ is a cusp, or point of return;
4) $2x^4-3x^2y+y^2-2y^3+y^4=0$; $(0,0)$ is a point of self-contact.
A non-singular point $x$ on the plane real algebraic curve $L$ defined by (1) is called a point of inflection if at $x$,
$$ \begin{equation} H(x, y) = \begin{vmatrix} \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x\partial y} & \frac{\partial f}{\partial x} \\ \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial f}{\partial y} \\ \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & 0 \end{vmatrix} = 0. \end{equation} $$ In other words, points of inflection are points at which $L$ intersects the curve $H$ defined by (3); $H$ is called the Hessian of $L$. The points of inflection on a curve $L$ correspond to points of return on the dual curve $L^*$.
The following relation (due to F. Klein, 1876) holds for any plane real algebraic curve:
$$n+2d+r = n^* + 2d^* + r^*,$$ where $n$ is the order of $L$, $n^*$ is its class, $r^*$ is the number of points of inflection on $L$, $d^*$ is the number of isolated double tangents to $L$ (double points on $L^*$), $r$ is the number of points of return on $L$ (points of inflection on $L^*$), and $d$ is the number of double points on $L$. See also Plücker formulas.
Any irreducible plane curve $L$ is birationally equivalent to an irreducible curve $L_0$ having only ordinary singularities.
The genus, or type, of a plane real algebraic curve $L$ is defined as the difference between the largest number of double points that $L$ can have and their actual number. The genus $p$ and the order $n$ of a curve $L$ are related by
$$2p=n(n-1)-\sum r_i(r_i - 1),$$ where the summation extends over the points of multiplicity $r_i$ for all $i$.
Curves of genus zero (also called rational or unicursal curves) have an important property: The coordinates of a point moving along such a curve can be expressed by rational functions $\xi$ and $\eta$ of some parameter $t$. In other words, curves of genus zero are birationally equivalent to a straight line. Unicursal curves have important applications. Let, for example, the equation of such a curve define $y$ as an algebraic function of $x$; then for any rational function $g(x, y)$, the indefinite integral
$$\int g(x, y) \ dz$$ can be expressed in terms of elementary functions.
Curves of genus 1 are closely related to elliptic functions (cf. Elliptic function) and are birationally equivalent to third-order curves without singularities. Certain curves of genus $p>1$ (so-called hyper-elliptic curves) are birationally equivalent to a curve of order $p+2$ having a unique singular point of multiplicity $p$.
The genus $p$ is a birational invariant, but two curves having the same genus are not necessarily birationally equivalent.
A complete classification has not yet been obtained (1983) for curves of order $n\ge 4$. An irreducible second-order curve is either an empty set, an ellipse, a hyperbola, or a parabola (see Second-order curve). These curves are non-singular and unicursal.
I. Newton (1704) proposed the first classification of curves of order three, and thus laid the basis of a systematic study of plane real algebraic curves. The basis of the classification is the subdivision of curves of order three into classes in accordance with the number and character of the infinite branches. The equation for the curve can be reduced to one of four canonical forms $A$, $B$, $C$, and $D$ by a suitable choice of the coordinate system; these are then divided into classes, subclasses and types (see scheme).
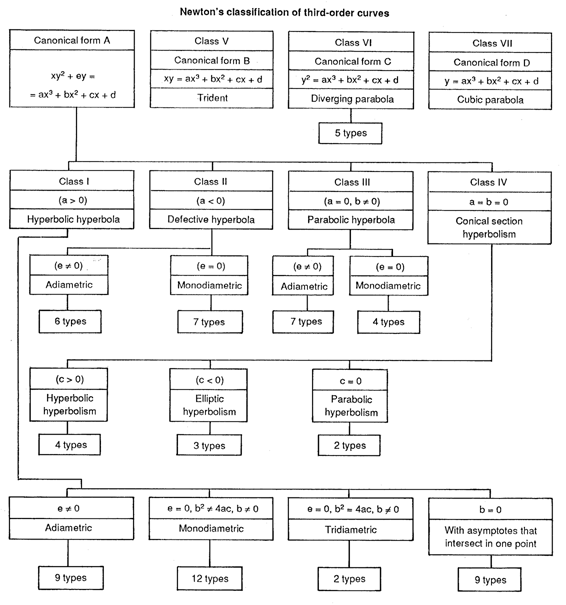
Figure: p072800a
Newton's classification of third-order curves.
For each third-order curve $L$ there is either a (unique) double point, and then $L$ is unicursal, or a point of inflection, which may lie at infinity; if there are three points of inflection, these lie on a single straight line, while there cannot be more than three points of inflection.
Completing the affine plane by elements at infinity leads to the projective plane, in which a plane real algebraic curve is defined by the equation
$$F(x^1, x^2, x^3) = 0,$$ where $F$ is a homogeneous polynomial of degree $n$ in the projective coordinates $x^1$, $x^2$ and $x^3$. The projective classification of curves is simpler; for example, any third-order curve can be considered as a section of a cone with as directrix one of the five so-called divergent parabolas, i.e. there are five types of projectively-inequivalent cubic curves (Newton's theorem).
When investing plane real algebraic curves it is also useful to use complex numbers and to transfer to the complex plane. See Algebraic curve.
References
| [1] | R.J. Walker, "Algebraic curves" , Springer (1978) MR0513824 Zbl 0399.14016 |
| [2] | A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian) |
| [3] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
See also Real algebraic variety.
The appellations "adiametric" , "monodiametric" , "tridiametric" are not commonly used in the West.
A Cremona transformation is a birational isomorphism of a projective space. I.e., in homogeneous coordinates on $P^n(\C)$ it is given by $(x_0, \ldots, x_n) \mapsto (F_0(x_0, \ldots, x_n), \ldots, F_n(x_0, \ldots, x_n))$, where the $F_i$ are homogeneous polynomials, all of the same order. In the case of the plane it is a theorem of I.R. Shafarevich that all Cremona transformations can be obtained by blowing up a number of points and then blowing down the same number of exceptional curves of the first kind.
References
| [a1] | E. Brieskorn, H. Knörrer, "Plane algebraic curves" , Birkhäuser (1986) (Translated from German) MR0886476 Zbl 0588.14019 |
Plane real algebraic curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plane_real_algebraic_curve&oldid=43800