Difference between revisions of "Cochleoid"
From Encyclopedia of Mathematics
(Comment: inversion yields quadratrix of Hippias, ref Lawrence) |
(gather refs) |
||
| Line 8: | Line 8: | ||
\rho = a\frac{\sin\varphi}{\varphi}. | \rho = a\frac{\sin\varphi}{\varphi}. | ||
\end{equation} | \end{equation} | ||
| − | |||
The cochleoid has infinitely many spirals, passing through its pole and touching the polar axis (see Fig.). The pole is a singular point of infinite multiplicity. Any straight line through the pole $O$ intersects the cochleoid; the tangents to the cochleoid at these intersection points pass through the same point. | The cochleoid has infinitely many spirals, passing through its pole and touching the polar axis (see Fig.). The pole is a singular point of infinite multiplicity. Any straight line through the pole $O$ intersects the cochleoid; the tangents to the cochleoid at these intersection points pass through the same point. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The [[Inversion|inverse]] of the cochleoid with respect to the origin is the [[quadratrix of Hippias]]. | The [[Inversion|inverse]] of the cochleoid with respect to the origin is the [[quadratrix of Hippias]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) ISBN 0-486-60288-5 {{ZBL|0257.50002}}</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) ISBN 0-486-60288-5 {{ZBL|0257.50002}}</TD></TR> | ||
| + | </table> | ||
Revision as of 11:16, 9 April 2023
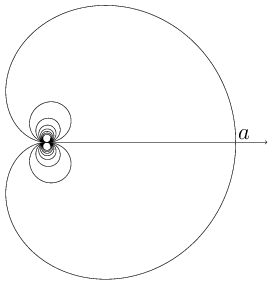
Figure 1. The cochleoid (pdf)
A plane transcendental curve whose equation in polar coordinates is \begin{equation} \rho = a\frac{\sin\varphi}{\varphi}. \end{equation}
The cochleoid has infinitely many spirals, passing through its pole and touching the polar axis (see Fig.). The pole is a singular point of infinite multiplicity. Any straight line through the pole $O$ intersects the cochleoid; the tangents to the cochleoid at these intersection points pass through the same point.
The inverse of the cochleoid with respect to the origin is the quadratrix of Hippias.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover (1972) ISBN 0-486-60288-5 Zbl 0257.50002 |
How to Cite This Entry:
Cochleoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cochleoid&oldid=42500
Cochleoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cochleoid&oldid=42500
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article