Difference between revisions of "D0L-sequence"
m (typo) |
(links) |
||
| Line 24: | Line 24: | ||
As already hinted at, the major mathematical importance of D$0$L-systems lies in the fact that they (in particular, the research on the D$0$L-sequence equivalence problem) motivated a large amount of fundamental research on morphisms of free monoids. Below a few such examples are given. | As already hinted at, the major mathematical importance of D$0$L-systems lies in the fact that they (in particular, the research on the D$0$L-sequence equivalence problem) motivated a large amount of fundamental research on morphisms of free monoids. Below a few such examples are given. | ||
| − | Consider a [[morphism]] $h : \Sigma^* \rightarrow \Sigma^*$ satisfying $h(a) = au$ for some $a \in \Sigma$ and $u \in \Sigma^{+}$. If $h$ is ''non-erasing'', i.e. $h(b) \neq 1$ for all $b \in \Sigma$, then there exists a unique infinite word | + | Consider a [[morphism]] $h : \Sigma^* \rightarrow \Sigma^*$ satisfying $h(a) = au$ for some $a \in \Sigma$ and $u \in \Sigma^{+}$. If $h$ is ''non-erasing'', i.e. $h(b) \neq 1$ for all $b \in \Sigma$, then there exists a unique infinite ''[[morphic word]]'' |
$$ | $$ | ||
w_h = \lim_{i \rightarrow \infty} h^i(a) \ . | w_h = \lim_{i \rightarrow \infty} h^i(a) \ . | ||
$$ | $$ | ||
| − | Consequently, D$0$L-sequences can be used in a very natural way to define infinite words. Implicitly, A. Thue used this approach at the beginning of the 20th century in his seminal work on square- and cube-free infinite words over a finite alphabet, see [[#References|[a16]]]. Since the early 1980s, such a research on non-repetitive words, revitalized by [[#References|[a2]]], has been a central topic in the combinatorics of words. Almost exclusively non-repetitive words are constructed by the above method of iterating a morphism. | + | Consequently, D$0$L-sequences can be used in a very natural way to define infinite words. Implicitly, A. Thue used this approach at the beginning of the 20th century in his seminal work on [[square-free]] and cube-free infinite words over a finite alphabet, see [[#References|[a16]]]. Since the early 1980s, such a research on non-repetitive words, revitalized by [[#References|[a2]]], has been a central topic in the combinatorics of words. Almost exclusively non-repetitive words are constructed by the above method of iterating a morphism. |
The D$0$L-sequence equivalence problem asks whether or not two morphisms $f$ and $g$ agree on a D$0$L-language defined by one of the morphisms, that is, whether or not $f(x) = g(x)$ for all $x$ in $\{ h^i(a) : i \ge 0 \}$. This has motivated the consideration of so-called equality languages of two morphisms $f,g : \Sigma^* \rightarrow \Delta^*$: | The D$0$L-sequence equivalence problem asks whether or not two morphisms $f$ and $g$ agree on a D$0$L-language defined by one of the morphisms, that is, whether or not $f(x) = g(x)$ for all $x$ in $\{ h^i(a) : i \ge 0 \}$. This has motivated the consideration of so-called equality languages of two morphisms $f,g : \Sigma^* \rightarrow \Delta^*$: | ||
Revision as of 20:21, 30 December 2015
$L$-systems were introduced by A. Lindenmayer in the late 1960s to model (in discrete time) the development of filamentous organisms. A fundamental feature of these systems is that in each step each cell (represented by a symbol from a finite alphabet) has to be rewritten according to the developmental rules of the organism. This parallelism is the main difference between $L$-systems and the classical Chomsky grammars (cf. also Grammar, generative). In fact, soon after their introduction, $L$-systems constituted a significant part of formal language theory, allowing one to compare parallel rewriting to a more classical sequential one, see [a13].
The simplest $L$-system is a so-called D$0$L-system, where the development starts from a single word and continues deterministically step by step in a context independent way, that is, the development of a symbol depends only on that symbol. (Here, "D" stands for determinism, $0$ for zero-sided interaction and "L" for Lindenmayer.) Formally, a D$0$L-system is a triple $\mathcal{G} = (\Sigma,h,w)$, where $\Sigma$ is a finite alphabet, $h$ is an endomorphism of the free monoid generated by $\Sigma$, in symbols $\Sigma^*$, and $w$ is a starting word. The system $\mathcal{G}$ defines the D$0$L-sequence $$ S(\mathcal{G})\ : \ w,\,h(w),\,h^2(w),\,\ldots $$ the D$0$L-growth sequence $$ GS(\mathcal{G})\ : \ |w|,\,|h(w)|,\,|h^2(w)|,\,\ldots $$ where $| \cdot |$ denotes the length of a word, and the D$0$L-language $$ L(\mathcal{G}) = \{ h^i(w) : i \ge 0 \} \ . $$
It is not only the mathematical simplicity of the definitions, but rather the challenging mathematical problems connected with these notions, in particular with D$0$L-sequences, which made D$0$L-systems mathematically very fruitful. The most famous problem is the D$0$L-sequence equivalence problem, which asks for an algorithm to decide whether or not two D$0$L-sequences coincide. The impact of this nice problem is discussed in [a11].
D$0$L-languages emphasize a static nature of the systems and are more related to classical formal language theory. D$0$L-growth sequences, in turn, are closely connected to the theory of $\mathbf{N}$-rational formal power series, and in fact allow one to reformulate certain classical problems, such as the algorithmic problem on the existence of a zero in a sequence defined by a linear recurrence, see [a15]. Finally, D$0$L-sequences represent a dynamical feature of the systems. Moreover, such sequences are defined in a very simple and natural way: by iterating a morphism.
The D$0$L-sequence equivalence problem was first shown to be algorithmically decidable in [a4] (cf. also Proof theory). A simpler solution was found in [a7], and finally a third completely different solution can be based on the validity of the Ehrenfeucht conjecture and Makanin's algorithm for the solvability of word equations over free monoids, as shown in [a6]. It is interesting to note that only the third solution extends to a multi-dimensional variant of the D$0$L-problem, the so-called DT$0$L-sequence equivalence problem. In the latter problem, the word sequences of (a1) are replaced by $k$-ary trees obtained by iterating $k$ different morphisms in all possible ways.
Despite the above solutions, an intriguing feature of the D$0$L-sequence equivalence problem remains. Indeed, none of the above solutions is practical. However, it has been conjectured that only the $2.\mathrm{card}(\Sigma)$ first elements of the sequences have to be compared in order to decide the equivalence. This $2n$-conjecture is known to hold when $\Sigma$ is binary, see [a10], but no reasonable (even exponential) bound is known (1998) in the general case.
As already hinted at, the major mathematical importance of D$0$L-systems lies in the fact that they (in particular, the research on the D$0$L-sequence equivalence problem) motivated a large amount of fundamental research on morphisms of free monoids. Below a few such examples are given.
Consider a morphism $h : \Sigma^* \rightarrow \Sigma^*$ satisfying $h(a) = au$ for some $a \in \Sigma$ and $u \in \Sigma^{+}$. If $h$ is non-erasing, i.e. $h(b) \neq 1$ for all $b \in \Sigma$, then there exists a unique infinite morphic word $$ w_h = \lim_{i \rightarrow \infty} h^i(a) \ . $$
Consequently, D$0$L-sequences can be used in a very natural way to define infinite words. Implicitly, A. Thue used this approach at the beginning of the 20th century in his seminal work on square-free and cube-free infinite words over a finite alphabet, see [a16]. Since the early 1980s, such a research on non-repetitive words, revitalized by [a2], has been a central topic in the combinatorics of words. Almost exclusively non-repetitive words are constructed by the above method of iterating a morphism.
The D$0$L-sequence equivalence problem asks whether or not two morphisms $f$ and $g$ agree on a D$0$L-language defined by one of the morphisms, that is, whether or not $f(x) = g(x)$ for all $x$ in $\{ h^i(a) : i \ge 0 \}$. This has motivated the consideration of so-called equality languages of two morphisms $f,g : \Sigma^* \rightarrow \Delta^*$: $$ E(f,g) = \{ x \in \Sigma^* : f(x) = g(x) \} \ . $$
Research on equality languages revealed amazing morphic characterizations of recursively enumerable languages, see [a3], [a8] and [a14]. For example, each recursively enumerable language (cf. also Formal languages and automata) can be expressed in the form $L = \pi(E(f,g) \cap R)$, where $\pi$, $f$ and $g$ are morphisms and $R$ is a regular language (cf. also Grammar, regular). Furthermore, the fundamental Post correspondence problem can be formulated as a problem of deciding whether or not $E(f,g) = \{1\}$, where $1$ denotes the unit of the free monoid $\Sigma^*$.
A third, and apparently the most fundamental, consequence of research on D$0$L-systems was a discovery of a compactness property of free semi-groups: Each system of equations over a free monoid containing a finite number of variables is equivalent to some of its finite subsystems (cf. also Free semi-group). This property (often referred to as the Ehrenfeucht conjecture) was conjectured by A. Ehrenfeucht in the early 1970s (in a slightly different form) and later established in [a1] and [a9].
Finally, it is worth mentioning that besides their mathematical inspiration, D$0$L-sequences have turned out to be useful in areas such as computer graphics and simulation of biological developments, see [a5] and [a12].
References
| [a1] | M. Albert, J. Lawrence, "A proof of Ehrenfeucht's conjecture" Theoret. Comput. Sci. , 41 (1985) pp. 121–123 |
| [a2] | J. Bertel, "Mots sans carré et morphismes itérés" Discrete Math. , 29 (1979) pp. 235–244 |
| [a3] | K. Culik II, "A purely homomorphic characterization of recursively enumerable sets" J. Assoc. Comput. Mach. , 26 (1979) pp. 345–350 |
| [a4] | K. Culik II, I. Fris, "The decidability of the equivalence problem for D0L-systems" Inform. Control , 35 (1977) pp. 20–39 |
| [a5] | K. Culik II, J. Kari, "On the power of 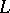 -systems in image generation" G. Rozenberg (ed.) A. Salomaa (ed.) , Developments in Language Theory , World Sci. (1994) pp. 225–236 -systems in image generation" G. Rozenberg (ed.) A. Salomaa (ed.) , Developments in Language Theory , World Sci. (1994) pp. 225–236 |
| [a6] | K. Culik II, J. Karhumäki, "Systems of equations over a free monoid and Ehrenfeucht's Conjecture" Discrete Math. , 43 (1983) pp. 139–153 |
| [a7] | A. Ehrenfeucht, G. Rozenberg, "Elementary homomorphisms and a solution to D$0$L-sequence equivalence problem" Theoret. Comput. Sci. , 7 (1978) pp. 169–183 |
| [a8] | J. Engelfriet, G. Rozenberg, "Fixed point languages, equality languages, and representation of recursively enumerable languages" J. Assoc. Comput. Mach. , 27 (1980) pp. 499–518 |
| [a9] | V.S. Guba, "The equivalence of infinite systems of equations in free groups and semigroups with finite subsystems" Mat. Zametki , 40 (1986) pp. 321–324 (In Russian) |
| [a10] | J. Karhumäki, "On the equivalence problem for binary D0L systems" Inform. Control , 50 (1981) pp. 276–284 |
| [a11] | J. Karhumäki, "The impact of the D$0$L-problem" G. Rozenberg (ed.) A. Salomaa (ed.) , Current Trends in Theoretical Computer Science. Essays and Tutorials , World Sci. (1993) pp. 586–594 |
| [a12] | P. Prusinkiewicz, M. Hammel, J. Hanan, R. Měch, "Visual models of plant development" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , III , Springer (1997) pp. 535–597 |
| [a13] | G. Rozenberg, A. Salomaa, "The mathematical theory of $L$-systems" , Acad. Press (1980) |
| [a14] | A. Salomaa, "Equality sets for homomorphisms of free monoids" Acta Cybernetica , 4 (1978) pp. 127–139 |
| [a15] | A. Salomaa, M. Soittola, "Automata-theoretic aspects of formal power series" , Springer (1978) |
| [a16] | A. Thue, "Über unendliche Zeichereichen" Kra. Vidensk. Selsk. Skr. I. Mat.-Nat. Kl. , 7 (1906) |
D0L-sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=D0L-sequence&oldid=37188