Difference between revisions of "Cornu spiral"
(TeX) |
m (link) |
||
| Line 2: | Line 2: | ||
''clothoid'' | ''clothoid'' | ||
| − | A transcendental plane curve (see Fig.) whose natural equation is | + | A transcendental plane curve (see Fig.) whose [[natural equation]] is |
$$r=\frac as,$$ | $$r=\frac as,$$ | ||
| Line 10: | Line 10: | ||
$$x=\int\limits_0^t\cos\frac{s^2}{2a}ds,\quad y=\int\limits_0^t\sin\frac{s^2}{2a}ds,$$ | $$x=\int\limits_0^t\cos\frac{s^2}{2a}ds,\quad y=\int\limits_0^t\sin\frac{s^2}{2a}ds,$$ | ||
| − | which are well-known in diffraction theory. The spiral of Cornu touches the horizontal axis at the origin. The asymptotic points are $M_1(\sqrt{\pi a}/2,\sqrt{\pi a}/2)$ and $ | + | which are well-known in diffraction theory. The spiral of Cornu touches the horizontal axis at the origin. The asymptotic points are $M_1(\sqrt{\pi a}/2,\sqrt{\pi a}/2)$ and $M_2(-\sqrt{\pi a}/2,-\sqrt{\pi a}/2)$. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c026510a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c026510a.gif" /> | ||
| Line 19: | Line 19: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966)</TD></TR> | ||
| + | </table> | ||
| Line 27: | Line 29: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) </TD></TR> | ||
| + | </table> | ||
Revision as of 12:00, 17 September 2017
clothoid
A transcendental plane curve (see Fig.) whose natural equation is
$$r=\frac as,$$
where $r$ is the radius of curvature, $a=\text{const}$ and $s$ is the arc length. It can be parametrized by the Fresnel integrals
$$x=\int\limits_0^t\cos\frac{s^2}{2a}ds,\quad y=\int\limits_0^t\sin\frac{s^2}{2a}ds,$$
which are well-known in diffraction theory. The spiral of Cornu touches the horizontal axis at the origin. The asymptotic points are $M_1(\sqrt{\pi a}/2,\sqrt{\pi a}/2)$ and $M_2(-\sqrt{\pi a}/2,-\sqrt{\pi a}/2)$.
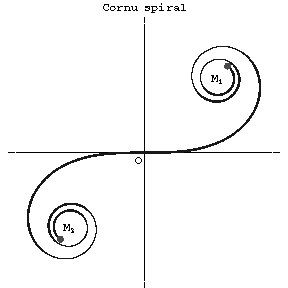
Figure: c026510a
The spiral of Cornu is sometimes called the spiral of Euler after L. Euler, who mentioned it first (1744). Beginning with the works of A. Cornu (1874), the spiral of Cornu is widely used in the calculation of diffraction of light.
References
| [1] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
Cornu spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cornu_spiral&oldid=32541