|
|
| Line 1: |
Line 1: |
| − | A set of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728001.png" /> in the real affine plane (cf. [[Affine space|Affine space]]) whose coordinates satisfy | + | {{TEX|done}} |
| | + | A set of points $L$ in the real affine plane (cf. |
| | + | [[Affine space|Affine space]]) whose coordinates satisfy |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728002.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table>
| + | $$f(x, y)=0,$$ |
| | + | where $f(x, y)$ is a |
| | + | [[Polynomial|polynomial]] of degree $n$ in the coordinates $x$ and $y$; the number $n$ is called the order of the curve $L$. If $f$ is a reducible polynomial, i.e. if it splits into factors $f_1, \ldots, f_k$, then the curve $L$ defined by (1) is called reducible and is the union of the curves $L_1, \ldots, L_k$ (the components of $L$) defined, correspondingly, by the equations |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728003.png" /> is a [[Polynomial|polynomial]] of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728004.png" /> in the coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728005.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728006.png" />; the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728007.png" /> is called the order of the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728008.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p0728009.png" /> is a reducible polynomial, i.e. if it splits into factors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280010.png" />, then the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280011.png" /> defined by (1) is called reducible and is the union of the curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280012.png" /> (the components of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280013.png" />) defined, correspondingly, by the equations
| + | $$f_1 = 0, \ldots, f_k = 0.$$ |
| | + | If on the other hand $f$ is an irreducible polynomial, $L$ is called an irreducible curve. Two irreducible plane real algebraic curves, one of order $n$ and the other of order $m$, intersect in at most $mn$ points (Bezout's theorem). |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280014.png" /></td> </tr></table>
| + | A given plane real algebraic curve $L$ can be defined by different equations. Let $I_L$ be the set of polynomials that vanish at all points of $L$. If $L$ is irreducible, then $fg=0$ on $L$ implies that $f$ or $g$ is zero; in that case the quotient ring $K_L = K/I_L$ does not have divisors of zero (cf. |
| | + | [[Zero divisor|Zero divisor]]) and is called the ring of polynomials on $L$ (here $K$ is the ring of all polynomials). |
| | | | |
| − | If on the other hand <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280015.png" /> is an irreducible polynomial, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280016.png" /> is called an irreducible curve. Two irreducible plane real algebraic curves, one of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280017.png" /> and the other of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280018.png" />, intersect in at most <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280019.png" /> points (Bezout's theorem).
| + | With an irreducible plane real algebraic curve $L$ one associates also a certain |
| | + | [[Field|field]] $K(L)$, called the field of rational functions on $L$. It consists of the rational functions $p(x, y)/q(x, y)$, where $q$ is not divisible by $f$, considered up to equality on $L$ ($p/q$ and $\tilde p/\tilde q$ are called equal on the curve $L$ defined by (1) if the polynomial $p\tilde q - \tilde p q$ is divisible by $f$). The field $K(L)$ is the field of fractions of $K_L$ (cf. |
| | + | [[Fractions, ring of|Fractions, ring of]]). |
| | | | |
| − | A given plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280020.png" /> can be defined by different equations. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280021.png" /> be the set of polynomials that vanish at all points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280022.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280023.png" /> is irreducible, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280024.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280025.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280026.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280027.png" /> is zero; in that case the quotient ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280028.png" /> does not have divisors of zero (cf. [[Zero divisor|Zero divisor]]) and is called the ring of polynomials on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280029.png" /> (here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280030.png" /> is the ring of all polynomials). | + | A mapping $F:(x, y) \to (\phi(x, y), \psi(x, y))$ of the plane into itself is called regular on the plane real algebraic curve $L$ if $\phi, \psi \in K(L)$. Curves $L$ and $M$ are called isomorphic if there are regular mappings (correspondingly, on $L$ and $M$) $F:L\to M$ and $G:M\to L$ that are mutually inverse; then the rings $K(L)$ and $K(M)$ are isomorphic. In particular, affinely-equivalent curves are isomorphic. |
| | | | |
| − | With an irreducible plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280031.png" /> one associates also a certain [[Field|field]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280032.png" />, called the field of rational functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280033.png" />. It consists of the rational functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280034.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280035.png" /> is not divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280036.png" />, considered up to equality on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280037.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280039.png" /> are called equal on the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280040.png" /> defined by (1) if the polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280041.png" /> is divisible by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280042.png" />). The field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280043.png" /> is the field of fractions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280044.png" /> (cf. [[Fractions, ring of|Fractions, ring of]]).
| + | More generally, a rational mapping from a curve $L$ to a curve $M$ is represented by rational functions. It establishes a correspondence between all points on the curves apart from a finite number of them and is defined as follows. Let $f=0$ and $g=0$ be equations of $L$ and $M$, respectively; then a rational mapping $F$ is defined by a pair of rational functions $\phi$ and $\psi$ defined on $L$ and such that $g(\phi, \psi)=0$ on $M$. Two curves $L$ and $M$ are called birationally equivalent if there exist rational mappings from $L$ to $M$ and from $M$ to $L$ that are inverse to each other; here the fields $K(L)$ and $K(M)$ are isomorphic. Such rational mappings are called birational, or Cremona, transformations. All Cremona transformations on the plane are realized by the successive execution of the standard quadratic transformation $x\to 1/x$, $y \to 1/y$ and projective transformations. Birational equivalence is a coarser relation than isomorphism, but the classification of plane real algebraic curves from this point of view is simpler and easier to survey. |
| | | | |
| − | A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280045.png" /> of the plane into itself is called regular on the plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280046.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280047.png" />. Curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280048.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280049.png" /> are called isomorphic if there are regular mappings (correspondingly, on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280050.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280051.png" />) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280052.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280053.png" /> that are mutually inverse; then the rings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280055.png" /> are isomorphic. In particular, affinely-equivalent curves are isomorphic. | + | A very simple example of a rational mapping is a |
| | + | [[Projective transformation|projective transformation]]. An important part is played by the dual mapping of an irreducible curve $L$ distinct from a straight line into the curve $L^*$ dual to $L$, defined by the formulas: |
| | | | |
| − | More generally, a rational mapping from a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280056.png" /> to a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280057.png" /> is represented by rational functions. It establishes a correspondence between all points on the curves apart from a finite number of them and is defined as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280058.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280059.png" /> be equations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280060.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280061.png" />, respectively; then a rational mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280062.png" /> is defined by a pair of rational functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280063.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280064.png" /> defined on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280065.png" /> and such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280066.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280067.png" />. Two curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280068.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280069.png" /> are called birationally equivalent if there exist rational mappings from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280070.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280071.png" /> and from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280072.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280073.png" /> that are inverse to each other; here the fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280074.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280075.png" /> are isomorphic. Such rational mappings are called birational, or Cremona, transformations. All Cremona transformations on the plane are realized by the successive execution of the standard quadratic transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280076.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280077.png" /> and projective transformations. Birational equivalence is a coarser relation than isomorphism, but the classification of plane real algebraic curves from this point of view is simpler and easier to survey.
| + | $$ |
| | + | u = \frac{\frac{\partial f}{\partial x}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, \qquad |
| | + | u = \frac{\frac{\partial f}{\partial y}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, |
| | + | $$ |
| | + | where $f$ is a polynomial defining $L$. The equation |
| | | | |
| − | A very simple example of a rational mapping is a [[Projective transformation|projective transformation]]. An important part is played by the dual mapping of an irreducible curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280078.png" /> distinct from a straight line into the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280079.png" /> dual to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280080.png" />, defined by the formulas:
| + | $$g(u, v)=0$$ |
| | + | defining $L^*$, is obtained by eliminating $x$ and $y$ from (1) and (2). The relationship between the dual mapping and the |
| | + | [[Tangential transformation|tangential transformation]] means that the curve $L^*$ itself in some cases can be represented as the envelope of the family of straight lines tangent to $L$. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280081.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table>
| + | The order of $L^*$ is called the class $n^*$ of the curve $L$. The duality relation is reciprocal, i.e. $L^{**} = L$, and it is a reflection of the |
| | + | [[Duality principle|duality principle]] in projective geometry. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280082.png" /> is a polynomial defining <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280083.png" />. The equation
| + | A point $x$ on the plane real algebraic curve $L$ defined by (1) is called a singular point if $\text{grad } f = 0$ at $x$. The analysis of singularities is a necessary element in the investigation of $L$, but a complete classification of singularities is at present far from being complete (1990). |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280084.png" /></td> </tr></table>
| + | If all the derivatives of the polynomial $f$ up to and including order $r-1$ vanish at a point $x$, while the derivative of order $r$ differs from zero at $x$, then $x$ is called a point of multiplicity $r$, and it is called an ordinary point of multiplicity $r$ if there exist $r$ different tangents there. Examples of singular points are: |
| | | | |
| − | defining <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280085.png" />, is obtained by eliminating <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280087.png" /> from (1) and (2). The relationship between the dual mapping and the [[Tangential transformation|tangential transformation]] means that the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280088.png" /> itself in some cases can be represented as the envelope of the family of straight lines tangent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280089.png" />.
| + | 1) $x^3-x^2+y^2=0$; $(0,0)$ is an ordinary double point, a point of self-intersection; |
| | | | |
| − | The order of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280090.png" /> is called the class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280091.png" /> of the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280092.png" />. The duality relation is reciprocal, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280093.png" />, and it is a reflection of the [[Duality principle|duality principle]] in projective geometry.
| + | 2) $x^2+x^3+y^2=0$; $(0, 0)$ is an isolated point; |
| | | | |
| − | A point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280094.png" /> on the plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280095.png" /> defined by (1) is called a singular point if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280096.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280097.png" />. The analysis of singularities is a necessary element in the investigation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280098.png" />, but a complete classification of singularities is at present far from being complete (1990).
| + | 3) $x^3+y^2=0$; $(0,0)$ is a cusp, or point of return; |
| | | | |
| − | If all the derivatives of the polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p07280099.png" /> up to and including order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800100.png" /> vanish at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800101.png" />, while the derivative of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800102.png" /> differs from zero at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800103.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800104.png" /> is called a point of multiplicity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800105.png" />, and it is called an ordinary point of multiplicity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800107.png" /> if there exist <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800108.png" /> different tangents there. Examples of singular points are:
| + | 4) $2x^4-3x^2y+y^2-2y^3+y^4=0$; $(0,0)$ is a point of self-contact. |
| | | | |
| − | 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800109.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800110.png" /> is an ordinary double point, a point of self-intersection; | + | A non-singular point $x$ on the plane real algebraic curve $L$ defined by (1) is called a point of inflection if at $x$, |
| | | | |
| − | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800111.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800112.png" /> is an isolated point;
| + | $$H(x, y) = \begin{vmatrix} |
| − | | + | \frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x\partial y} & \frac{\partial f}{\partial x} \\ |
| − | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800113.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800114.png" /> is a cusp, or point of return;
| + | \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial f}{\partial y} \\ |
| − | | + | \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & 0 |
| − | 4) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800115.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800116.png" /> is a point of self-contact.
| + | \end{vmatrix} = 0. |
| − | | + | $$ |
| − | A non-singular point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800117.png" /> on the plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800118.png" /> defined by (1) is called a point of inflection if at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800119.png" />,
| + | In other words, points of inflection are points at which $L$ intersects the curve $H$ defined by (3); $H$ is called the Hessian of $L$. The points of inflection on a curve $L$ correspond to points of return on the dual curve $L^*$. |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800120.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table>
| |
| − | | |
| − | In other words, points of inflection are points at which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800121.png" /> intersects the curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800122.png" /> defined by (3); <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800123.png" /> is called the Hessian of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800124.png" />. The points of inflection on a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800125.png" /> correspond to points of return on the dual curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800126.png" />. | |
| | | | |
| | The following relation (due to F. Klein, 1876) holds for any plane real algebraic curve: | | The following relation (due to F. Klein, 1876) holds for any plane real algebraic curve: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800127.png" /></td> </tr></table>
| + | $$n+2d+r = n^* + 2d^* + r^*,$$ |
| | + | where $n$ is the order of $L$, $n^*$ is its class, $r^*$ is the number of points of inflection on $L$, $d^*$ is the number of isolated double tangents to $L$ (double points on $L^*$), $r$ is the number of points of return on $L$ (points of inflection on $L^*$), and $d$ is the number of double points on $L$. See also |
| | + | [[Plücker formulas|Plücker formulas]]. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800128.png" /> is the order of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800129.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800130.png" /> is its class, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800131.png" /> is the number of points of inflection on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800132.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800133.png" /> is the number of isolated double tangents to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800134.png" /> (double points on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800135.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800136.png" /> is the number of points of return on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800137.png" /> (points of inflection on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800138.png" />), and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800139.png" /> is the number of double points on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800140.png" />. See also [[Plücker formulas|Plücker formulas]].
| + | Any irreducible plane curve $L$ is birationally equivalent to an irreducible curve $L_0$ having only ordinary singularities. |
| | | | |
| − | Any irreducible plane curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800141.png" /> is birationally equivalent to an irreducible curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800142.png" /> having only ordinary singularities.
| + | The genus, or type, of a plane real algebraic curve $L$ is defined as the difference between the largest number of double points that $L$ can have and their actual number. The genus $p$ and the order $n$ of a curve $L$ are related by |
| | | | |
| − | The genus, or type, of a plane real algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800143.png" /> is defined as the difference between the largest number of double points that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800144.png" /> can have and their actual number. The genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800145.png" /> and the order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800146.png" /> of a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800147.png" /> are related by
| + | $$2p=n(n-1)-\sum r_i(r_i - 1),$$ |
| | + | where the summation extends over the points of multiplicity $r_i$ for all $i$. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800148.png" /></td> </tr></table>
| + | Curves of genus zero (also called rational or unicursal curves) have an important property: The coordinates of a point moving along such a curve can be expressed by rational functions $\xi$ and $\eta$ of some parameter $t$. In other words, curves of genus zero are birationally equivalent to a straight line. Unicursal curves have important applications. Let, for example, the equation of such a curve define $y$ as an algebraic function of $x$; then for any rational function $g(x, y)$, the indefinite integral |
| − | | |
| − | where the summation extends over the points of multiplicity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800149.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800150.png" />.
| |
| − | | |
| − | Curves of genus zero (also called rational or unicursal curves) have an important property: The coordinates of a point moving along such a curve can be expressed by rational functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800151.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800152.png" /> of some parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800153.png" />. In other words, curves of genus zero are birationally equivalent to a straight line. Unicursal curves have important applications. Let, for example, the equation of such a curve define <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800154.png" /> as an algebraic function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800155.png" />; then for any rational function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800156.png" />, the indefinite integral | |
| − | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800157.png" /></td> </tr></table>
| |
| | | | |
| | + | $$\int g(x, y) \ dz$$ |
| | can be expressed in terms of elementary functions. | | can be expressed in terms of elementary functions. |
| | | | |
| − | Curves of genus 1 are closely related to elliptic functions (cf. [[Elliptic function|Elliptic function]]) and are birationally equivalent to third-order curves without singularities. Certain curves of genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800158.png" /> (so-called hyper-elliptic curves) are birationally equivalent to a curve of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800159.png" /> having a unique singular point of multiplicity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800160.png" />. | + | Curves of genus 1 are closely related to elliptic functions (cf. |
| | + | [[Elliptic function|Elliptic function]]) and are birationally equivalent to third-order curves without singularities. Certain curves of genus $p>1$ (so-called hyper-elliptic curves) are birationally equivalent to a curve of order $p+2$ having a unique singular point of multiplicity $p$. |
| | | | |
| − | The genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800161.png" /> is a birational invariant, but two curves having the same genus are not necessarily birationally equivalent. | + | The genus $p$ is a birational invariant, but two curves having the same genus are not necessarily birationally equivalent. |
| | | | |
| − | A complete classification has not yet been obtained (1983) for curves of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800162.png" />. An irreducible second-order curve is either an empty set, an ellipse, a hyperbola, or a parabola (see [[Second-order curve|Second-order curve]]). These curves are non-singular and unicursal. | + | A complete classification has not yet been obtained (1983) for curves of order $n\ge 4$. An irreducible second-order curve is either an empty set, an ellipse, a hyperbola, or a parabola (see |
| | + | [[Second-order curve|Second-order curve]]). These curves are non-singular and unicursal. |
| | | | |
| − | I. Newton (1704) proposed the first classification of curves of order three, and thus laid the basis of a systematic study of plane real algebraic curves. The basis of the classification is the subdivision of curves of order three into classes in accordance with the number and character of the infinite branches. The equation for the curve can be reduced to one of four canonical forms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800163.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800164.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800165.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800166.png" /> by a suitable choice of the coordinate system; these are then divided into classes, subclasses and types (see scheme). | + | I. Newton (1704) proposed the first classification of curves of order three, and thus laid the basis of a systematic study of plane real algebraic curves. The basis of the classification is the subdivision of curves of order three into classes in accordance with the number and character of the infinite branches. The equation for the curve can be reduced to one of four canonical forms $A$, $B$, $C$, and $D$ by a suitable choice of the coordinate system; these are then divided into classes, subclasses and types (see scheme). |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p072800a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p072800a.gif" /> |
| Line 81: |
Line 93: |
| | Newton's classification of third-order curves. | | Newton's classification of third-order curves. |
| | | | |
| − | For each third-order curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800167.png" /> there is either a (unique) double point, and then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800168.png" /> is unicursal, or a point of inflection, which may lie at infinity; if there are three points of inflection, these lie on a single straight line, while there cannot be more than three points of inflection. | + | For each third-order curve $L$ there is either a (unique) double point, and then $L$ is unicursal, or a point of inflection, which may lie at infinity; if there are three points of inflection, these lie on a single straight line, while there cannot be more than three points of inflection. |
| | | | |
| | Completing the affine plane by elements at infinity leads to the projective plane, in which a plane real algebraic curve is defined by the equation | | Completing the affine plane by elements at infinity leads to the projective plane, in which a plane real algebraic curve is defined by the equation |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800169.png" /></td> </tr></table>
| + | $$F(x^1, x^2, x^3) = 0,$$ |
| − | | + | where $F$ is a homogeneous polynomial of degree $n$ in the projective coordinates $x^1$, $x^2$ and $x^3$. The projective classification of curves is simpler; for example, any third-order curve can be considered as a section of a cone with as directrix one of the five so-called divergent parabolas, i.e. there are five types of projectively-inequivalent cubic curves (Newton's theorem). |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800170.png" /> is a homogeneous polynomial of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800171.png" /> in the projective coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800172.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800173.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800174.png" />. The projective classification of curves is simpler; for example, any third-order curve can be considered as a section of a cone with as directrix one of the five so-called divergent parabolas, i.e. there are five types of projectively-inequivalent cubic curves (Newton's theorem). | |
| | | | |
| − | When investing plane real algebraic curves it is also useful to use complex numbers and to transfer to the complex plane. See [[Algebraic curve|Algebraic curve]]. | + | When investing plane real algebraic curves it is also useful to use complex numbers and to transfer to the complex plane. See |
| | + | [[Algebraic curve|Algebraic curve]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.J. Walker, "Algebraic curves" , Springer (1978) {{MR|0513824}} {{ZBL|0399.14016}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> |
| | + | <TD valign="top"> R.J. Walker, "Algebraic curves" , Springer (1978) {{MR|0513824}} {{ZBL|0399.14016}} </TD> |
| | + | </TR><TR><TD valign="top">[2]</TD> |
| | + | <TD valign="top"> A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)</TD> |
| | + | </TR><TR><TD valign="top">[3]</TD> |
| | + | <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD> |
| | + | </TR></table> |
| | | | |
| | | | |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | See also [[Real algebraic variety|Real algebraic variety]]. | + | See also |
| | + | [[Real algebraic variety|Real algebraic variety]]. |
| | | | |
| | The appellations "adiametric" , "monodiametric" , "tridiametric" are not commonly used in the West. | | The appellations "adiametric" , "monodiametric" , "tridiametric" are not commonly used in the West. |
| | | | |
| − | A [[Cremona transformation|Cremona transformation]] is a birational isomorphism of a projective space. I.e., in homogeneous coordinates on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800175.png" /> it is given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800176.png" />, where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p072/p072800/p072800177.png" /> are homogeneous polynomials, all of the same order. In the case of the plane it is a theorem of I.R. Shafarevich that all Cremona transformations can be obtained by blowing up a number of points and then blowing down the same number of exceptional curves of the first kind. | + | A |
| | + | [[Cremona transformation|Cremona transformation]] is a birational isomorphism of a projective space. I.e., in homogeneous coordinates on $P^n(\C)$ it is given by $(x_0, \ldots, x_n) \mapsto (F_0(x_0, \ldots, x_n), \ldots, F_n(x_0, \ldots, x_n))$, where the $F_i$ are homogeneous polynomials, all of the same order. In the case of the plane it is a theorem of I.R. Shafarevich that all Cremona transformations can be obtained by blowing up a number of points and then blowing down the same number of exceptional curves of the first kind. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Brieskorn, H. Knörrer, "Plane algebraic curves" , Birkhäuser (1986) (Translated from German) {{MR|0886476}} {{ZBL|0588.14019}} </TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> |
| | + | <TD valign="top"> E. Brieskorn, H. Knörrer, "Plane algebraic curves" , Birkhäuser (1986) (Translated from German) {{MR|0886476}} {{ZBL|0588.14019}} </TD> |
| | + | </TR></table> |
A set of points $L$ in the real affine plane (cf.
Affine space) whose coordinates satisfy
$$f(x, y)=0,$$
where $f(x, y)$ is a
polynomial of degree $n$ in the coordinates $x$ and $y$; the number $n$ is called the order of the curve $L$. If $f$ is a reducible polynomial, i.e. if it splits into factors $f_1, \ldots, f_k$, then the curve $L$ defined by (1) is called reducible and is the union of the curves $L_1, \ldots, L_k$ (the components of $L$) defined, correspondingly, by the equations
$$f_1 = 0, \ldots, f_k = 0.$$
If on the other hand $f$ is an irreducible polynomial, $L$ is called an irreducible curve. Two irreducible plane real algebraic curves, one of order $n$ and the other of order $m$, intersect in at most $mn$ points (Bezout's theorem).
A given plane real algebraic curve $L$ can be defined by different equations. Let $I_L$ be the set of polynomials that vanish at all points of $L$. If $L$ is irreducible, then $fg=0$ on $L$ implies that $f$ or $g$ is zero; in that case the quotient ring $K_L = K/I_L$ does not have divisors of zero (cf.
Zero divisor) and is called the ring of polynomials on $L$ (here $K$ is the ring of all polynomials).
With an irreducible plane real algebraic curve $L$ one associates also a certain
field $K(L)$, called the field of rational functions on $L$. It consists of the rational functions $p(x, y)/q(x, y)$, where $q$ is not divisible by $f$, considered up to equality on $L$ ($p/q$ and $\tilde p/\tilde q$ are called equal on the curve $L$ defined by (1) if the polynomial $p\tilde q - \tilde p q$ is divisible by $f$). The field $K(L)$ is the field of fractions of $K_L$ (cf.
Fractions, ring of).
A mapping $F:(x, y) \to (\phi(x, y), \psi(x, y))$ of the plane into itself is called regular on the plane real algebraic curve $L$ if $\phi, \psi \in K(L)$. Curves $L$ and $M$ are called isomorphic if there are regular mappings (correspondingly, on $L$ and $M$) $F:L\to M$ and $G:M\to L$ that are mutually inverse; then the rings $K(L)$ and $K(M)$ are isomorphic. In particular, affinely-equivalent curves are isomorphic.
More generally, a rational mapping from a curve $L$ to a curve $M$ is represented by rational functions. It establishes a correspondence between all points on the curves apart from a finite number of them and is defined as follows. Let $f=0$ and $g=0$ be equations of $L$ and $M$, respectively; then a rational mapping $F$ is defined by a pair of rational functions $\phi$ and $\psi$ defined on $L$ and such that $g(\phi, \psi)=0$ on $M$. Two curves $L$ and $M$ are called birationally equivalent if there exist rational mappings from $L$ to $M$ and from $M$ to $L$ that are inverse to each other; here the fields $K(L)$ and $K(M)$ are isomorphic. Such rational mappings are called birational, or Cremona, transformations. All Cremona transformations on the plane are realized by the successive execution of the standard quadratic transformation $x\to 1/x$, $y \to 1/y$ and projective transformations. Birational equivalence is a coarser relation than isomorphism, but the classification of plane real algebraic curves from this point of view is simpler and easier to survey.
A very simple example of a rational mapping is a
projective transformation. An important part is played by the dual mapping of an irreducible curve $L$ distinct from a straight line into the curve $L^*$ dual to $L$, defined by the formulas:
$$
u = \frac{\frac{\partial f}{\partial x}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}}, \qquad
u = \frac{\frac{\partial f}{\partial y}}{f - x \frac{\partial f}{\partial x} - y \frac{\partial f}{\partial y}},
$$
where $f$ is a polynomial defining $L$. The equation
$$g(u, v)=0$$
defining $L^*$, is obtained by eliminating $x$ and $y$ from (1) and (2). The relationship between the dual mapping and the
tangential transformation means that the curve $L^*$ itself in some cases can be represented as the envelope of the family of straight lines tangent to $L$.
The order of $L^*$ is called the class $n^*$ of the curve $L$. The duality relation is reciprocal, i.e. $L^{**} = L$, and it is a reflection of the
duality principle in projective geometry.
A point $x$ on the plane real algebraic curve $L$ defined by (1) is called a singular point if $\text{grad } f = 0$ at $x$. The analysis of singularities is a necessary element in the investigation of $L$, but a complete classification of singularities is at present far from being complete (1990).
If all the derivatives of the polynomial $f$ up to and including order $r-1$ vanish at a point $x$, while the derivative of order $r$ differs from zero at $x$, then $x$ is called a point of multiplicity $r$, and it is called an ordinary point of multiplicity $r$ if there exist $r$ different tangents there. Examples of singular points are:
1) $x^3-x^2+y^2=0$; $(0,0)$ is an ordinary double point, a point of self-intersection;
2) $x^2+x^3+y^2=0$; $(0, 0)$ is an isolated point;
3) $x^3+y^2=0$; $(0,0)$ is a cusp, or point of return;
4) $2x^4-3x^2y+y^2-2y^3+y^4=0$; $(0,0)$ is a point of self-contact.
A non-singular point $x$ on the plane real algebraic curve $L$ defined by (1) is called a point of inflection if at $x$,
$$H(x, y) = \begin{vmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x\partial y} & \frac{\partial f}{\partial x} \\
\frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial f}{\partial y} \\
\frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & 0
\end{vmatrix} = 0.
$$
In other words, points of inflection are points at which $L$ intersects the curve $H$ defined by (3); $H$ is called the Hessian of $L$. The points of inflection on a curve $L$ correspond to points of return on the dual curve $L^*$.
The following relation (due to F. Klein, 1876) holds for any plane real algebraic curve:
$$n+2d+r = n^* + 2d^* + r^*,$$
where $n$ is the order of $L$, $n^*$ is its class, $r^*$ is the number of points of inflection on $L$, $d^*$ is the number of isolated double tangents to $L$ (double points on $L^*$), $r$ is the number of points of return on $L$ (points of inflection on $L^*$), and $d$ is the number of double points on $L$. See also
Plücker formulas.
Any irreducible plane curve $L$ is birationally equivalent to an irreducible curve $L_0$ having only ordinary singularities.
The genus, or type, of a plane real algebraic curve $L$ is defined as the difference between the largest number of double points that $L$ can have and their actual number. The genus $p$ and the order $n$ of a curve $L$ are related by
$$2p=n(n-1)-\sum r_i(r_i - 1),$$
where the summation extends over the points of multiplicity $r_i$ for all $i$.
Curves of genus zero (also called rational or unicursal curves) have an important property: The coordinates of a point moving along such a curve can be expressed by rational functions $\xi$ and $\eta$ of some parameter $t$. In other words, curves of genus zero are birationally equivalent to a straight line. Unicursal curves have important applications. Let, for example, the equation of such a curve define $y$ as an algebraic function of $x$; then for any rational function $g(x, y)$, the indefinite integral
$$\int g(x, y) \ dz$$
can be expressed in terms of elementary functions.
Curves of genus 1 are closely related to elliptic functions (cf.
Elliptic function) and are birationally equivalent to third-order curves without singularities. Certain curves of genus $p>1$ (so-called hyper-elliptic curves) are birationally equivalent to a curve of order $p+2$ having a unique singular point of multiplicity $p$.
The genus $p$ is a birational invariant, but two curves having the same genus are not necessarily birationally equivalent.
A complete classification has not yet been obtained (1983) for curves of order $n\ge 4$. An irreducible second-order curve is either an empty set, an ellipse, a hyperbola, or a parabola (see
Second-order curve). These curves are non-singular and unicursal.
I. Newton (1704) proposed the first classification of curves of order three, and thus laid the basis of a systematic study of plane real algebraic curves. The basis of the classification is the subdivision of curves of order three into classes in accordance with the number and character of the infinite branches. The equation for the curve can be reduced to one of four canonical forms $A$, $B$, $C$, and $D$ by a suitable choice of the coordinate system; these are then divided into classes, subclasses and types (see scheme).
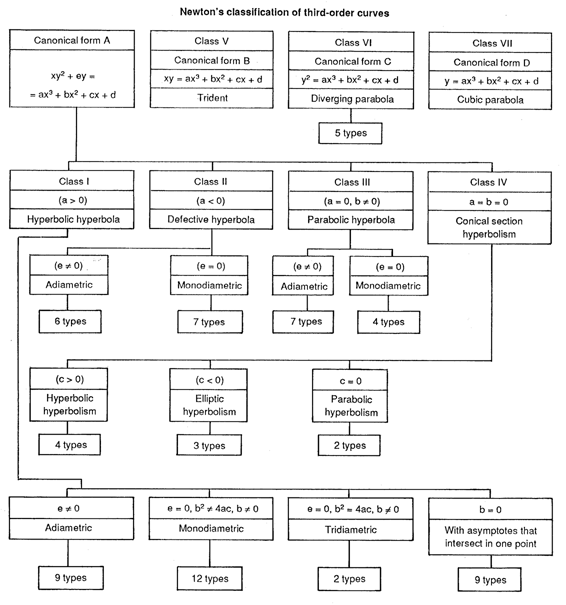
Figure: p072800a
Newton's classification of third-order curves.
For each third-order curve $L$ there is either a (unique) double point, and then $L$ is unicursal, or a point of inflection, which may lie at infinity; if there are three points of inflection, these lie on a single straight line, while there cannot be more than three points of inflection.
Completing the affine plane by elements at infinity leads to the projective plane, in which a plane real algebraic curve is defined by the equation
$$F(x^1, x^2, x^3) = 0,$$
where $F$ is a homogeneous polynomial of degree $n$ in the projective coordinates $x^1$, $x^2$ and $x^3$. The projective classification of curves is simpler; for example, any third-order curve can be considered as a section of a cone with as directrix one of the five so-called divergent parabolas, i.e. there are five types of projectively-inequivalent cubic curves (Newton's theorem).
When investing plane real algebraic curves it is also useful to use complex numbers and to transfer to the complex plane. See
Algebraic curve.
References
| [1] |
R.J. Walker, "Algebraic curves" , Springer (1978) MR0513824 Zbl 0399.14016 |
| [2] |
A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian) |
| [3] |
A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
See also
Real algebraic variety.
The appellations "adiametric" , "monodiametric" , "tridiametric" are not commonly used in the West.
A
Cremona transformation is a birational isomorphism of a projective space. I.e., in homogeneous coordinates on $P^n(\C)$ it is given by $(x_0, \ldots, x_n) \mapsto (F_0(x_0, \ldots, x_n), \ldots, F_n(x_0, \ldots, x_n))$, where the $F_i$ are homogeneous polynomials, all of the same order. In the case of the plane it is a theorem of I.R. Shafarevich that all Cremona transformations can be obtained by blowing up a number of points and then blowing down the same number of exceptional curves of the first kind.
References
| [a1] |
E. Brieskorn, H. Knörrer, "Plane algebraic curves" , Birkhäuser (1986) (Translated from German) MR0886476 Zbl 0588.14019 |
