|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m1302301.png" /> be a projective morphism of algebraic varieties over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m1302302.png" /> of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m1302303.png" /> (cf. also [[Algebraic variety|Algebraic variety]]). A relative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m1302306.png" />-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m1302307.png" />-cycle is a formal linear combination <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m1302308.png" /> of a finite number of curves <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m1302309.png" /> (reduced irreducible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023010.png" />-dimensional closed subschemes) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023011.png" /> with real number coefficients <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023012.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023013.png" /> are points on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023014.png" />. (If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023015.png" />, then the word "relative" is dropped.) Two relative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023016.png" />-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023017.png" />-cycles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023019.png" /> are said to be numerically equivalent if their intersection numbers are equal, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023022.png" /> for any Cartier divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023023.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023024.png" /> (cf. also [[Divisor|Divisor]]; [[Intersection index (in algebraic geometry)|Intersection index (in algebraic geometry)]]). The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023025.png" /> of all the equivalence classes of relative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023026.png" />-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023027.png" />-cycles with respect to the numerical equivalence becomes a finite-dimensional real [[Vector space|vector space]]. The closed cone of curves (the Kleiman–Mori cone) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023028.png" /> is defined to be the closed convex cone in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023029.png" /> generated by the classes of curves on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023030.png" /> which are mapped to points on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023031.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023032.png" />. A half-line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023033.png" /> is called an extremal ray if the inequality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023034.png" /> holds and if the equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023035.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023036.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023037.png" />.
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | + | |
| | + | Out of 155 formulas, 154 were replaced by TEX code.--> |
| | + | |
| | + | {{TEX|semi-auto}}{{TEX|partial}} |
| | + | Let $f : X \rightarrow S$ be a projective morphism of algebraic varieties over a field $k$ of characteristic $0$ (cf. also [[Algebraic variety|Algebraic variety]]). A relative $\mathbf{R}$-$1$-cycle is a formal linear combination $Z = \sum _ { i = 1 } ^ { t } r _ { j } C _ { j }$ of a finite number of curves $C_{j}$ (reduced irreducible $1$-dimensional closed subschemes) on $X$ with real number coefficients $r _ { j }$ such that $f ( C _ { j } )$ are points on $S$. (If $S = \operatorname{Spec} k$, then the word "relative" is dropped.) Two relative $\mathbf{R}$-$1$-cycles $Z _ { 1 }$ and $Z_2$ are said to be numerically equivalent if their intersection numbers are equal, $( D . Z _ { 1 } ) = ( D . Z _ { 2 } ) \in \bf R$ for any Cartier divisor $D$ on $X$ (cf. also [[Divisor|Divisor]]; [[Intersection index (in algebraic geometry)|Intersection index (in algebraic geometry)]]). The set $N _ { 1 } ( X / S )$ of all the equivalence classes of relative $\mathbf{R}$-$1$-cycles with respect to the numerical equivalence becomes a finite-dimensional real [[Vector space|vector space]]. The closed cone of curves (the Kleiman–Mori cone) $\overline { N E } ( X / S )$ is defined to be the closed convex cone in $N _ { 1 } ( X / S )$ generated by the classes of curves on $X$ which are mapped to points on $S$ by $f$. A half-line $R = {\bf R} _ { \geq 0 } v \subset \overline { N E } ( X / S )$ is called an extremal ray if the inequality $( ( K_{X} + B ) \cdot v ) < 0$ holds and if the equality $v = v _ { 1 } + v _ { 2 }$ for $v _ { 1 } , v _ { 2 } \in \overline { NE } ( X / S )$ implies $v _ { 1 } , v _ { 2 } \in R$. |
| | | | |
| | ===Cone theorem.=== | | ===Cone theorem.=== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023038.png" /> be a normal algebraic variety and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023039.png" /> an effective <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023040.png" />-divisor such that the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023041.png" /> is weakly log terminal (cf. [[Kawamata rationality theorem|Kawamata rationality theorem]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023042.png" /> be a projective morphism to another algebraic variety. Then there exist at most countably many extremal rays <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023043.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023044.png" />) satisfying the following conditions: | + | Let $X$ be a normal algebraic variety and $B$ an effective $\mathbf{Q}$-divisor such that the pair $( X , B )$ is weakly log terminal (cf. [[Kawamata rationality theorem|Kawamata rationality theorem]]). Let $f : X \rightarrow S$ be a projective morphism to another algebraic variety. Then there exist at most countably many extremal rays $R _ { j } = {\bf R} _ { \geq 0 } v_j$ ($j \in J$) satisfying the following conditions: |
| | | | |
| − | For any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023045.png" />, there exist an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023046.png" /> and numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023047.png" />, which are zero except for finitely many <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023048.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023050.png" />. | + | For any $v \in \overline { N E } ( X / S )$, there exist an element $v ^ { \prime } \in \overline { N E } ( X / S )$ and numbers $r _ { j } \in {\bf R} _ { \geq 0 }$, which are zero except for finitely many $j$, such that $( ( K _ { X } + B ) \cdot v ^ { \prime } ) \geq 0$ and $v = v ^ { \prime } + \sum_j r_j v_j$. |
| | | | |
| − | (discreteness) For any closed convex cone <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023051.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023052.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023053.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023054.png" />, there exist only finitely many <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023055.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023056.png" />. | + | (discreteness) For any closed convex cone $\Sigma$ in $N _ { 1 } ( X / S )$ such that $( ( K_{X} + B ) \cdot v ) < 0$ for any $v \in \Sigma \backslash \{ 0 \}$, there exist only finitely many $j \in J$ such that $v _ { j } \in \Sigma$. |
| | | | |
| | ===Contraction theorem.=== | | ===Contraction theorem.=== |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023057.png" /> be an extremal ray as above. Then there exists a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023058.png" />, called a contraction morphism, to a normal algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023059.png" /> with a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023060.png" /> which is characterized by the following properties: | + | Let $R$ be an extremal ray as above. Then there exists a morphism $\phi : X \rightarrow Y$, called a contraction morphism, to a normal algebraic variety $Y$ with a morphism $g : Y \rightarrow S$ which is characterized by the following properties: |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023061.png" />;
| + | $g \circ \phi = f$; |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023062.png" />;
| + | $\phi_{*} {\cal O} _ { X } = {\cal O} _ { Y }$; |
| | | | |
| − | any curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023063.png" /> which is mapped to a point by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023064.png" /> is mapped to a point by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023065.png" /> if and only if its numerical class belongs to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023066.png" />. | + | any curve $C$ which is mapped to a point by $f$ is mapped to a point by $\phi$ if and only if its numerical class belongs to $R$. |
| | | | |
| − | Two methods of proofs for the cone theorem are known. The first one [[#References|[a6]]] uses a deformation theory of morphisms over a field of positive characteristic and applies only in the case where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023067.png" /> is smooth. It is important to note that this is the only known method in mathematics to prove the existence of rational curves (as of 2000). The second approach [[#References|[a2]]] uses a vanishing theorem of cohomology groups (cf. [[Kawamata–Viehweg vanishing theorem|Kawamata–Viehweg vanishing theorem]]) which is true only in characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023068.png" />. This method of proof, which is obtained via a rationality theorem (cf. [[Kawamata rationality theorem|Kawamata rationality theorem]]), applies also to singular varieties and easily extends to the logarithmic version as explained above. The contraction theorem has been proved only by a characteristic-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023069.png" /> method (cf. [[#References|[a1]]]). | + | Two methods of proofs for the cone theorem are known. The first one [[#References|[a6]]] uses a deformation theory of morphisms over a field of positive characteristic and applies only in the case where $X$ is smooth. It is important to note that this is the only known method in mathematics to prove the existence of rational curves (as of 2000). The second approach [[#References|[a2]]] uses a vanishing theorem of cohomology groups (cf. [[Kawamata–Viehweg vanishing theorem|Kawamata–Viehweg vanishing theorem]]) which is true only in characteristic $0$. This method of proof, which is obtained via a rationality theorem (cf. [[Kawamata rationality theorem|Kawamata rationality theorem]]), applies also to singular varieties and easily extends to the logarithmic version as explained above. The contraction theorem has been proved only by a characteristic-$0$ method (cf. [[#References|[a1]]]). |
| | | | |
| − | In the following it is also assumed that the variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023070.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023072.png" />-factorial, that is, for any prime divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023073.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023074.png" /> there exists a positive integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023075.png" />, depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023076.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023077.png" /> is a Cartier divisor. Then the contraction morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023078.png" /> is of one of the following types: | + | In the following it is also assumed that the variety $X$ is $\mathbf{Q}$-factorial, that is, for any prime divisor $D$ on $X$ there exists a positive integer $m$, depending on $D$, such that $m D$ is a Cartier divisor. Then the contraction morphism $\phi$ is of one of the following types: |
| | | | |
| − | (Fano–Mori fibre space) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023079.png" />. | + | (Fano–Mori fibre space) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023079.png"/>. |
| | | | |
| − | (divisorial contraction) There exists a prime divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023080.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023081.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023082.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023083.png" /> induces an isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023084.png" />. | + | (divisorial contraction) There exists a prime divisor $E$ of $X$ such that $\operatorname{codim}\phi ( E ) \geq 2$ and $\phi$ induces an isomorphism $X\backslash E \rightarrow Y \backslash \phi ( E )$. |
| | | | |
| − | (small contraction) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023085.png" /> is an isomorphism in codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023087.png" />, in the sense that there exists a closed subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023088.png" /> of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023089.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023090.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023091.png" /> induces an isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023092.png" />. | + | (small contraction) $\phi$ is an isomorphism in codimension $1$, in the sense that there exists a closed subset $E$ of codimension $\geq 2$ of $X$ such that $\phi$ induces an isomorphism $X\backslash E \rightarrow Y \backslash \phi ( E )$. |
| | | | |
| | ===Flip conjectures.=== | | ===Flip conjectures.=== |
| − | The first flip conjecture is as follows: Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023093.png" /> be a small contraction. Then there exists a birational morphism from a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023094.png" />-factorial normal algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023095.png" /> which is again an isomorphism in codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023096.png" /> and is such that the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023097.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023098.png" /> is weakly log terminal and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m13023099.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230100.png" />-ample <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230101.png" />-divisor (cf. also [[Divisor|Divisor]]). The diagram <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230102.png" /> is called a flip (or log flip). Note that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230103.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230104.png" />-ample. | + | The first flip conjecture is as follows: Let $\phi : X \rightarrow Y$ be a small contraction. Then there exists a birational morphism from a $\mathbf{Q}$-factorial normal algebraic variety $\phi ^ { + } : X ^ { + } \rightarrow Y$ which is again an isomorphism in codimension $1$ and is such that the pair $( X ^ { + } , B ^ { + } )$ with $B ^ { + } = ( \phi _ { * } ^ { + } ) ^ { - 1 } \phi_{ *} B$ is weakly log terminal and $K _ { X ^{+}} + B ^ { + }$ is a $\phi ^ { + }$-ample $\mathbf{Q}$-divisor (cf. also [[Divisor|Divisor]]). The diagram $X \rightarrow Y \leftarrow X ^ { + }$ is called a flip (or log flip). Note that $- ( K _ { X } + B )$ is $\phi$-ample. |
| | | | |
| | The second flip conjecture states that there does not exist an infinite sequence of consecutive flips. | | The second flip conjecture states that there does not exist an infinite sequence of consecutive flips. |
| | | | |
| − | There is no small contraction if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230105.png" />. The flip conjectures have been proved for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230106.png" /> (see [[#References|[a3]]], [[#References|[a4]]] for the first flip conjecture, and [[#References|[a5]]], [[#References|[a7]]] for the second). The proofs depend on the classification of singularities and it is hard to extend them to a higher-dimensional case. | + | There is no small contraction if $\operatorname{dim} X \leq 2$. The flip conjectures have been proved for $\operatorname { dim } X = 3$ (see [[#References|[a3]]], [[#References|[a4]]] for the first flip conjecture, and [[#References|[a5]]], [[#References|[a7]]] for the second). The proofs depend on the classification of singularities and it is hard to extend them to a higher-dimensional case. |
| | | | |
| | ===Minimal model program (MMP).=== | | ===Minimal model program (MMP).=== |
| − | Fix a base variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230107.png" /> and consider a [[Category|category]] whose objects are a pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230108.png" /> and a projective morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230109.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230110.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230111.png" />-factorial normal algebraic variety and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230112.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230113.png" />-divisor such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230114.png" /> is weakly log terminal. A morphism from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230115.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230116.png" /> in this category is a [[Birational mapping|birational mapping]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230117.png" /> which is surjective in codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230119.png" />, in the sense that any prime divisor on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230120.png" /> is the image of a prime divisor on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230121.png" />, and such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230122.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230123.png" />. The minimal model program is a program which works under the assumption that the flip conjectures hold. It starts from an arbitrary object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230124.png" /> and constructs a morphism to another object <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230125.png" /> such that one of the following holds: | + | Fix a base variety $S$ and consider a [[Category|category]] whose objects are a pair $( X , B )$ and a projective morphism $f : X \rightarrow S$ such that $X$ is a $\mathbf{Q}$-factorial normal algebraic variety and $B$ is a $\mathbf{Q}$-divisor such that $( X , B )$ is weakly log terminal. A morphism from $( ( X , B ) , f )$ to $( ( X ^ { \prime } , B ^ { \prime } ) , f ^ { \prime } )$ in this category is a [[Birational mapping|birational mapping]] $\alpha : X _ { .. } \rightarrow X ^ { \prime }$ which is surjective in codimension $1$, in the sense that any prime divisor on $X ^ { \prime }$ is the image of a prime divisor on $X$, and such that $B ^ { \prime } = \alpha_{*} B$ and $f ^ { \prime } \circ \alpha = f$. The minimal model program is a program which works under the assumption that the flip conjectures hold. It starts from an arbitrary object $( ( X , B ) , f )$ and constructs a morphism to another object $( ( X ^ { \prime } , B ^ { \prime } ) , f ^ { \prime } )$ such that one of the following holds: |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230126.png" /> has a Fano–Mori fibre space structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230127.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230128.png" />.
| + | $X ^ { \prime }$ has a Fano–Mori fibre space structure $\phi : X ^ { \prime } \rightarrow Y$ over $S$. |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230129.png" /> is minimal over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230130.png" /> in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230131.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230133.png" />-nef, i.e., an inequality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230134.png" /> holds for any curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230135.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230136.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230137.png" /> is a point on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230138.png" />. Construct objects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230139.png" /> inductively as follows. Set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230140.png" />. Suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230141.png" /> has already been constructed. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230142.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230143.png" />-nef, then a minimal model is obtained. If not, then, by the cone theorem, there exists an extremal ray and one obtains a contraction morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230144.png" /> by the contraction theorem. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230145.png" />, then a Fano–Mori fibre space is obtained. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230146.png" /> is a divisorial contraction, then one sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230147.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230148.png" /> is a small contraction and if the first flip conjecture is true, then take the flip <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230149.png" /> and set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230150.png" />. If the second flip conjecture is true, then this process stops after a finite number of steps.
| + | $X ^ { \prime }$ is minimal over $S$ in the sense that $K _ { X ^ { \prime } } + B ^ { \prime }$ is $f ^ { \prime }$-nef, i.e., an inequality $( ( K _ { X ^ { \prime } } + B ^ { \prime } ) . C ) \geq 0$ holds for any curve $C$ on $X ^ { \prime }$ such that $f ( C )$ is a point on $S$. Construct objects $( ( X _ { n } , B _ { n } ) , f _ { n } )$ inductively as follows. Set $( ( X _ { 0 } , B _ { 0 } ) , f _ { 0 } ) = ( ( X , B ) , f )$. Suppose that $( ( X _ { n } , B _ { n } ) , f _ { n } )$ has already been constructed. If $K _ { X _ { n } } + B _ { n }$ is $f _ { n }$-nef, then a minimal model is obtained. If not, then, by the cone theorem, there exists an extremal ray and one obtains a contraction morphism $\phi : X _ { n } \rightarrow Y$ by the contraction theorem. If $\operatorname { dim } Y < \operatorname { dim } X _ { n }$, then a Fano–Mori fibre space is obtained. If $\phi$ is a divisorial contraction, then one sets $( ( X _ { n + 1} , B _ { n + 1} ) , f _ { n + 1 } ) = ( ( Y , \phi_{ * } B _ { n } ) , f _ { n } \circ \phi ^ { - 1 } )$. If $\phi$ is a small contraction and if the first flip conjecture is true, then take the flip $\phi ^ { + } : X _ { n } ^ { + } \rightarrow Y$ and set $( ( X _ { n + 1 } , B _ { n + 1 } ) , f _ { n + 1 } ) = ( ( X _ { n } ^ { + } , ( \phi _ { * } ^ { + } ) ^ { - 1 } \phi _ { * } B _ { n } ) , f _ { n } \circ \phi ^ { - 1 } \circ \phi ^ { + } )$. If the second flip conjecture is true, then this process stops after a finite number of steps. |
| | | | |
| − | A normal algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230151.png" /> is said to be terminal, or it is said that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230152.png" /> has only terminal singularities, if the following conditions are satisfied: | + | A normal algebraic variety $X$ is said to be terminal, or it is said that $X$ has only terminal singularities, if the following conditions are satisfied: |
| | | | |
| − | 1) The canonical divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230153.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230154.png" />-Cartier divisor. | + | 1) The canonical divisor $K _ { X }$ is a $\mathbf{Q}$-Cartier divisor. |
| | | | |
| − | 2) There exists a projective birational morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230155.png" /> from a smooth variety with a normal crossing divisor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230156.png" /> such that one can write <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230157.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230158.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230159.png" />. | + | 2) There exists a projective birational morphism $\mu : Y \rightarrow X$ from a smooth variety with a normal crossing divisor $D = \sum _ { k = 1 } ^ { s } D _ { k }$ such that one can write $\mu ^ { * } K _ { X } = K _ { Y } + \sum _ { k } d _ { k } D _ { k }$ with $d _ { k } < 0$ for all $k$. |
| | | | |
| − | As a special case of the minimal model program, if one assumes that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230160.png" /> has only terminal singularities and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230161.png" />, then any subsequent pair satisfies the same condition that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230162.png" /> has only terminal singularities and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m130/m130230/m130230163.png" />. This is the "non-log" version. | + | As a special case of the minimal model program, if one assumes that $X$ has only terminal singularities and $B = 0$, then any subsequent pair satisfies the same condition that $X_n$ has only terminal singularities and $B _ { n } = 0$. This is the "non-log" version. |
| | | | |
| | It is expected that the minimal model program works also over a field of arbitrary characteristic, although the cone and contraction theorems are conjectural in general. | | It is expected that the minimal model program works also over a field of arbitrary characteristic, although the cone and contraction theorems are conjectural in general. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" ''Adv. Stud. Pure Math.'' , '''10''' (1987) pp. 283–360 {{MR|0946243}} {{ZBL|0672.14006}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> Y. Kawamata, "The cone of curves of algebraic varieties" ''Ann. of Math.'' , '''119''' (1984) pp. 603–633 {{MR|0750714}} {{MR|0744865}} {{ZBL|0544.14009}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Mori, "Flip theorem and the existence of minimal models for 3-folds" ''J. Amer. Math. Soc.'' , '''1''' (1988) pp. 117–253 {{MR|0924704}} {{ZBL|0649.14023}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> V. Shokurov, "3-fold log flips" ''Izv. Russian Akad. Nauk.'' , '''56''' (1992) pp. 105–203 {{MR|}} {{ZBL|0785.14023}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> V. Shokurov, "The nonvanishing theorem" ''Izv. Akad. Nauk. SSSR'' , '''49''' (1985) pp. 635–651 {{MR|794958}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> S. Mori, "Threefolds whose canonical bundles are not numerically effective" ''Ann. of Math.'' , '''116''' (1982) pp. 133–176 {{MR|}} {{ZBL|0557.14021}} {{ZBL|0493.14020}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> Y. Kawamata, "Termination of log-flips for algebraic 3-folds" ''Internat. J. Math.'' , '''3''' (1992) pp. 653–659 {{MR|1189678}} {{ZBL|0814.14016}} </TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" ''Adv. Stud. Pure Math.'' , '''10''' (1987) pp. 283–360 {{MR|0946243}} {{ZBL|0672.14006}} </td></tr><tr><td valign="top">[a2]</td> <td valign="top"> Y. Kawamata, "The cone of curves of algebraic varieties" ''Ann. of Math.'' , '''119''' (1984) pp. 603–633 {{MR|0750714}} {{MR|0744865}} {{ZBL|0544.14009}} </td></tr><tr><td valign="top">[a3]</td> <td valign="top"> S. Mori, "Flip theorem and the existence of minimal models for 3-folds" ''J. Amer. Math. Soc.'' , '''1''' (1988) pp. 117–253 {{MR|0924704}} {{ZBL|0649.14023}} </td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V. Shokurov, "3-fold log flips" ''Izv. Russian Akad. Nauk.'' , '''56''' (1992) pp. 105–203 {{MR|}} {{ZBL|0785.14023}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> V. Shokurov, "The nonvanishing theorem" ''Izv. Akad. Nauk. SSSR'' , '''49''' (1985) pp. 635–651 {{MR|794958}} {{ZBL|}} </td></tr><tr><td valign="top">[a6]</td> <td valign="top"> S. Mori, "Threefolds whose canonical bundles are not numerically effective" ''Ann. of Math.'' , '''116''' (1982) pp. 133–176 {{MR|}} {{ZBL|0557.14021}} {{ZBL|0493.14020}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> Y. Kawamata, "Termination of log-flips for algebraic 3-folds" ''Internat. J. Math.'' , '''3''' (1992) pp. 653–659 {{MR|1189678}} {{ZBL|0814.14016}} </td></tr></table> |
Let $f : X \rightarrow S$ be a projective morphism of algebraic varieties over a field $k$ of characteristic $0$ (cf. also Algebraic variety). A relative $\mathbf{R}$-$1$-cycle is a formal linear combination $Z = \sum _ { i = 1 } ^ { t } r _ { j } C _ { j }$ of a finite number of curves $C_{j}$ (reduced irreducible $1$-dimensional closed subschemes) on $X$ with real number coefficients $r _ { j }$ such that $f ( C _ { j } )$ are points on $S$. (If $S = \operatorname{Spec} k$, then the word "relative" is dropped.) Two relative $\mathbf{R}$-$1$-cycles $Z _ { 1 }$ and $Z_2$ are said to be numerically equivalent if their intersection numbers are equal, $( D . Z _ { 1 } ) = ( D . Z _ { 2 } ) \in \bf R$ for any Cartier divisor $D$ on $X$ (cf. also Divisor; Intersection index (in algebraic geometry)). The set $N _ { 1 } ( X / S )$ of all the equivalence classes of relative $\mathbf{R}$-$1$-cycles with respect to the numerical equivalence becomes a finite-dimensional real vector space. The closed cone of curves (the Kleiman–Mori cone) $\overline { N E } ( X / S )$ is defined to be the closed convex cone in $N _ { 1 } ( X / S )$ generated by the classes of curves on $X$ which are mapped to points on $S$ by $f$. A half-line $R = {\bf R} _ { \geq 0 } v \subset \overline { N E } ( X / S )$ is called an extremal ray if the inequality $( ( K_{X} + B ) \cdot v ) < 0$ holds and if the equality $v = v _ { 1 } + v _ { 2 }$ for $v _ { 1 } , v _ { 2 } \in \overline { NE } ( X / S )$ implies $v _ { 1 } , v _ { 2 } \in R$.
Cone theorem.
Let $X$ be a normal algebraic variety and $B$ an effective $\mathbf{Q}$-divisor such that the pair $( X , B )$ is weakly log terminal (cf. Kawamata rationality theorem). Let $f : X \rightarrow S$ be a projective morphism to another algebraic variety. Then there exist at most countably many extremal rays $R _ { j } = {\bf R} _ { \geq 0 } v_j$ ($j \in J$) satisfying the following conditions:
For any $v \in \overline { N E } ( X / S )$, there exist an element $v ^ { \prime } \in \overline { N E } ( X / S )$ and numbers $r _ { j } \in {\bf R} _ { \geq 0 }$, which are zero except for finitely many $j$, such that $( ( K _ { X } + B ) \cdot v ^ { \prime } ) \geq 0$ and $v = v ^ { \prime } + \sum_j r_j v_j$.
(discreteness) For any closed convex cone $\Sigma$ in $N _ { 1 } ( X / S )$ such that $( ( K_{X} + B ) \cdot v ) < 0$ for any $v \in \Sigma \backslash \{ 0 \}$, there exist only finitely many $j \in J$ such that $v _ { j } \in \Sigma$.
Contraction theorem.
Let $R$ be an extremal ray as above. Then there exists a morphism $\phi : X \rightarrow Y$, called a contraction morphism, to a normal algebraic variety $Y$ with a morphism $g : Y \rightarrow S$ which is characterized by the following properties:
$g \circ \phi = f$;
$\phi_{*} {\cal O} _ { X } = {\cal O} _ { Y }$;
any curve $C$ which is mapped to a point by $f$ is mapped to a point by $\phi$ if and only if its numerical class belongs to $R$.
Two methods of proofs for the cone theorem are known. The first one [a6] uses a deformation theory of morphisms over a field of positive characteristic and applies only in the case where $X$ is smooth. It is important to note that this is the only known method in mathematics to prove the existence of rational curves (as of 2000). The second approach [a2] uses a vanishing theorem of cohomology groups (cf. Kawamata–Viehweg vanishing theorem) which is true only in characteristic $0$. This method of proof, which is obtained via a rationality theorem (cf. Kawamata rationality theorem), applies also to singular varieties and easily extends to the logarithmic version as explained above. The contraction theorem has been proved only by a characteristic-$0$ method (cf. [a1]).
In the following it is also assumed that the variety $X$ is $\mathbf{Q}$-factorial, that is, for any prime divisor $D$ on $X$ there exists a positive integer $m$, depending on $D$, such that $m D$ is a Cartier divisor. Then the contraction morphism $\phi$ is of one of the following types:
(Fano–Mori fibre space) 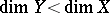 .
.
(divisorial contraction) There exists a prime divisor $E$ of $X$ such that $\operatorname{codim}\phi ( E ) \geq 2$ and $\phi$ induces an isomorphism $X\backslash E \rightarrow Y \backslash \phi ( E )$.
(small contraction) $\phi$ is an isomorphism in codimension $1$, in the sense that there exists a closed subset $E$ of codimension $\geq 2$ of $X$ such that $\phi$ induces an isomorphism $X\backslash E \rightarrow Y \backslash \phi ( E )$.
Flip conjectures.
The first flip conjecture is as follows: Let $\phi : X \rightarrow Y$ be a small contraction. Then there exists a birational morphism from a $\mathbf{Q}$-factorial normal algebraic variety $\phi ^ { + } : X ^ { + } \rightarrow Y$ which is again an isomorphism in codimension $1$ and is such that the pair $( X ^ { + } , B ^ { + } )$ with $B ^ { + } = ( \phi _ { * } ^ { + } ) ^ { - 1 } \phi_{ *} B$ is weakly log terminal and $K _ { X ^{+}} + B ^ { + }$ is a $\phi ^ { + }$-ample $\mathbf{Q}$-divisor (cf. also Divisor). The diagram $X \rightarrow Y \leftarrow X ^ { + }$ is called a flip (or log flip). Note that $- ( K _ { X } + B )$ is $\phi$-ample.
The second flip conjecture states that there does not exist an infinite sequence of consecutive flips.
There is no small contraction if $\operatorname{dim} X \leq 2$. The flip conjectures have been proved for $\operatorname { dim } X = 3$ (see [a3], [a4] for the first flip conjecture, and [a5], [a7] for the second). The proofs depend on the classification of singularities and it is hard to extend them to a higher-dimensional case.
Minimal model program (MMP).
Fix a base variety $S$ and consider a category whose objects are a pair $( X , B )$ and a projective morphism $f : X \rightarrow S$ such that $X$ is a $\mathbf{Q}$-factorial normal algebraic variety and $B$ is a $\mathbf{Q}$-divisor such that $( X , B )$ is weakly log terminal. A morphism from $( ( X , B ) , f )$ to $( ( X ^ { \prime } , B ^ { \prime } ) , f ^ { \prime } )$ in this category is a birational mapping $\alpha : X _ { .. } \rightarrow X ^ { \prime }$ which is surjective in codimension $1$, in the sense that any prime divisor on $X ^ { \prime }$ is the image of a prime divisor on $X$, and such that $B ^ { \prime } = \alpha_{*} B$ and $f ^ { \prime } \circ \alpha = f$. The minimal model program is a program which works under the assumption that the flip conjectures hold. It starts from an arbitrary object $( ( X , B ) , f )$ and constructs a morphism to another object $( ( X ^ { \prime } , B ^ { \prime } ) , f ^ { \prime } )$ such that one of the following holds:
$X ^ { \prime }$ has a Fano–Mori fibre space structure $\phi : X ^ { \prime } \rightarrow Y$ over $S$.
$X ^ { \prime }$ is minimal over $S$ in the sense that $K _ { X ^ { \prime } } + B ^ { \prime }$ is $f ^ { \prime }$-nef, i.e., an inequality $( ( K _ { X ^ { \prime } } + B ^ { \prime } ) . C ) \geq 0$ holds for any curve $C$ on $X ^ { \prime }$ such that $f ( C )$ is a point on $S$. Construct objects $( ( X _ { n } , B _ { n } ) , f _ { n } )$ inductively as follows. Set $( ( X _ { 0 } , B _ { 0 } ) , f _ { 0 } ) = ( ( X , B ) , f )$. Suppose that $( ( X _ { n } , B _ { n } ) , f _ { n } )$ has already been constructed. If $K _ { X _ { n } } + B _ { n }$ is $f _ { n }$-nef, then a minimal model is obtained. If not, then, by the cone theorem, there exists an extremal ray and one obtains a contraction morphism $\phi : X _ { n } \rightarrow Y$ by the contraction theorem. If $\operatorname { dim } Y < \operatorname { dim } X _ { n }$, then a Fano–Mori fibre space is obtained. If $\phi$ is a divisorial contraction, then one sets $( ( X _ { n + 1} , B _ { n + 1} ) , f _ { n + 1 } ) = ( ( Y , \phi_{ * } B _ { n } ) , f _ { n } \circ \phi ^ { - 1 } )$. If $\phi$ is a small contraction and if the first flip conjecture is true, then take the flip $\phi ^ { + } : X _ { n } ^ { + } \rightarrow Y$ and set $( ( X _ { n + 1 } , B _ { n + 1 } ) , f _ { n + 1 } ) = ( ( X _ { n } ^ { + } , ( \phi _ { * } ^ { + } ) ^ { - 1 } \phi _ { * } B _ { n } ) , f _ { n } \circ \phi ^ { - 1 } \circ \phi ^ { + } )$. If the second flip conjecture is true, then this process stops after a finite number of steps.
A normal algebraic variety $X$ is said to be terminal, or it is said that $X$ has only terminal singularities, if the following conditions are satisfied:
1) The canonical divisor $K _ { X }$ is a $\mathbf{Q}$-Cartier divisor.
2) There exists a projective birational morphism $\mu : Y \rightarrow X$ from a smooth variety with a normal crossing divisor $D = \sum _ { k = 1 } ^ { s } D _ { k }$ such that one can write $\mu ^ { * } K _ { X } = K _ { Y } + \sum _ { k } d _ { k } D _ { k }$ with $d _ { k } < 0$ for all $k$.
As a special case of the minimal model program, if one assumes that $X$ has only terminal singularities and $B = 0$, then any subsequent pair satisfies the same condition that $X_n$ has only terminal singularities and $B _ { n } = 0$. This is the "non-log" version.
It is expected that the minimal model program works also over a field of arbitrary characteristic, although the cone and contraction theorems are conjectural in general.
References
| [a1] | Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" Adv. Stud. Pure Math. , 10 (1987) pp. 283–360 MR0946243 Zbl 0672.14006 |
| [a2] | Y. Kawamata, "The cone of curves of algebraic varieties" Ann. of Math. , 119 (1984) pp. 603–633 MR0750714 MR0744865 Zbl 0544.14009 |
| [a3] | S. Mori, "Flip theorem and the existence of minimal models for 3-folds" J. Amer. Math. Soc. , 1 (1988) pp. 117–253 MR0924704 Zbl 0649.14023 |
| [a4] | V. Shokurov, "3-fold log flips" Izv. Russian Akad. Nauk. , 56 (1992) pp. 105–203 Zbl 0785.14023 |
| [a5] | V. Shokurov, "The nonvanishing theorem" Izv. Akad. Nauk. SSSR , 49 (1985) pp. 635–651 MR794958 |
| [a6] | S. Mori, "Threefolds whose canonical bundles are not numerically effective" Ann. of Math. , 116 (1982) pp. 133–176 Zbl 0557.14021 Zbl 0493.14020 |
| [a7] | Y. Kawamata, "Termination of log-flips for algebraic 3-folds" Internat. J. Math. , 3 (1992) pp. 653–659 MR1189678 Zbl 0814.14016 |
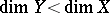 .
.