Difference between revisions of "Operator ergodic theorem"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 3: | Line 3: | ||
[[Category:General theory of linear operators]] | [[Category:General theory of linear operators]] | ||
| − | A general name for theorems on the limit of means along an unboundedly lengthening "time interval" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683601.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683602.png" />, for the powers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683603.png" /> of a [[Linear operator|linear operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683604.png" /> acting on a Banach space (or even on a topological vector space, see | + | A general name for theorems on the limit of means along an unboundedly lengthening "time interval" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683601.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683602.png" />, for the powers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683603.png" /> of a [[Linear operator|linear operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683604.png" /> acting on a Banach space (or even on a topological vector space, see {{Cite|KSS}}) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683605.png" />, or for a [[One-parameter semi-group|one-parameter semi-group]] of linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683606.png" /> acting on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683607.png" /> (cf. also [[Ergodic theorem|Ergodic theorem]]). In the latter case one can also examine the limit of means along an unboundedly diminishing time interval (local ergodic theorems, see {{Cite|KSS}}, {{Cite|K}}; one also speaks of "ergodicity at zero" , see {{Cite|HP}}). Means can be understood in various senses in the same way as in the theory of summation of series. The most frequently used means are the Cesàro means |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683608.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683608.png" /></td> </tr></table> | ||
| Line 11: | Line 11: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683609.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o0683609.png" /></td> </tr></table> | ||
| − | and the Abel means, | + | and the Abel means, {{Cite|HP}}, |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836010.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836010.png" /></td> </tr></table> | ||
| Line 19: | Line 19: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836011.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836011.png" /></td> </tr></table> | ||
| − | The conditions of ergodic theorems automatically ensure the convergence of these infinite series or integrals; under these conditions, although the Abel means are formed by using all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836012.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836013.png" />, the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836014.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836015.png" /> in a finite period of time, unboundedly increasing when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836016.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836017.png" />), play a major part. The limit of the means (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836018.png" />, etc.) can be understood in various senses: In the strong or weak [[Operator topology|operator topology]] (statistical ergodic theorems, i.e. the [[Von Neumann ergodic theorem|von Neumann ergodic theorem]] — historically the first operator ergodic theorem — and its generalizations), in the uniform operator topology (uniform ergodic theorems, see | + | The conditions of ergodic theorems automatically ensure the convergence of these infinite series or integrals; under these conditions, although the Abel means are formed by using all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836012.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836013.png" />, the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836014.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836015.png" /> in a finite period of time, unboundedly increasing when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836016.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836017.png" />), play a major part. The limit of the means (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836018.png" />, etc.) can be understood in various senses: In the strong or weak [[Operator topology|operator topology]] (statistical ergodic theorems, i.e. the [[Von Neumann ergodic theorem|von Neumann ergodic theorem]] — historically the first operator ergodic theorem — and its generalizations), in the uniform operator topology (uniform ergodic theorems, see {{Cite|HP}}, {{Cite|DS}}, {{Cite|N}}), while if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836019.png" /> is a function space on a measure space, then also in the sense of almost-everywhere convergence of the means <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836020.png" />, etc., where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836021.png" /> (individual ergodic theorems, i.e. the [[Birkhoff ergodic theorem|Birkhoff ergodic theorem]] and its generalizations; see, for example, the [[Ornstein–Chacon ergodic theorem|Ornstein–Chacon ergodic theorem]]; these are not always called operator ergodic theorems, however). Some operator ergodic theorems compare the force of various of the above-mentioned variants with each other, establishing that, from the existence of limits of means in one sense, it follows that limits exist in another sense {{Cite|HP}}. Some theorems speak not of the limit of means, but of the limit of the ratios of two means (e.g. the Ornstein–Chacon theorem). |
There are also operator ergodic theorems for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836022.png" />-parameter and even more general semi-groups. | There are also operator ergodic theorems for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068360/o06836022.png" />-parameter and even more general semi-groups. | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|HP}}|| E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) {{MR|0089373}} {{ZBL|0392.46001}} {{ZBL|0033.06501}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|DS}}|| N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Wiley (1988) {{MR|1009164}} {{MR|1009163}} {{MR|1009162}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|N}}|| J. Neveu, "Mathematical foundations of the calculus of probabilities" , Holden-Day (1965) (Translated from French) {{MR|0198505}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|VY}}|| A.M. Vershik, S.A. Yuzvinskii, "Dynamical systems with invariant measure" ''Progress in Math.'' , '''8''' (1970) pp. 151–215 ''Itogi Nauk. Mat. Anal.'' , '''967''' (1969) pp. 133–187 {{MR|0286981}} {{ZBL|0252.28006}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|KSS}}|| A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" ''J. Soviet Math.'' , '''7''' : 2 (1977) pp. 974–1041 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''13''' (1975) pp. 129–262 {{MR|0584389}} {{ZBL|0399.28011}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|K}}|| U. Krengel, "Recent progress in ergodic theorems" ''Astérisque'' , '''50''' (1977) pp. 151–192 {{MR|486418}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|K2}}|| U. Krengel, "Ergodic theorems" , de Gruyter (1985) {{MR|0797411}} {{ZBL|0575.28009}} | ||
| + | |} | ||
Revision as of 18:10, 26 May 2012
2020 Mathematics Subject Classification: Primary: 47A35 [MSN][ZBL]
A general name for theorems on the limit of means along an unboundedly lengthening "time interval"  , or
, or  , for the powers
, for the powers  of a linear operator
of a linear operator  acting on a Banach space (or even on a topological vector space, see [KSS])
acting on a Banach space (or even on a topological vector space, see [KSS])  , or for a one-parameter semi-group of linear operators
, or for a one-parameter semi-group of linear operators  acting on
acting on  (cf. also Ergodic theorem). In the latter case one can also examine the limit of means along an unboundedly diminishing time interval (local ergodic theorems, see [KSS], [K]; one also speaks of "ergodicity at zero" , see [HP]). Means can be understood in various senses in the same way as in the theory of summation of series. The most frequently used means are the Cesàro means
(cf. also Ergodic theorem). In the latter case one can also examine the limit of means along an unboundedly diminishing time interval (local ergodic theorems, see [KSS], [K]; one also speaks of "ergodicity at zero" , see [HP]). Means can be understood in various senses in the same way as in the theory of summation of series. The most frequently used means are the Cesàro means
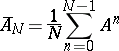 |
or
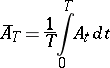 |
and the Abel means, [HP],
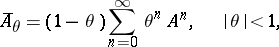 |
or
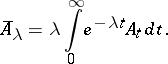 |
The conditions of ergodic theorems automatically ensure the convergence of these infinite series or integrals; under these conditions, although the Abel means are formed by using all 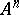 or
or 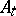 , the values of
, the values of 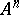 or
or 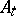 in a finite period of time, unboundedly increasing when
in a finite period of time, unboundedly increasing when 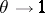 (or
(or  ), play a major part. The limit of the means (
), play a major part. The limit of the means ( , etc.) can be understood in various senses: In the strong or weak operator topology (statistical ergodic theorems, i.e. the von Neumann ergodic theorem — historically the first operator ergodic theorem — and its generalizations), in the uniform operator topology (uniform ergodic theorems, see [HP], [DS], [N]), while if
, etc.) can be understood in various senses: In the strong or weak operator topology (statistical ergodic theorems, i.e. the von Neumann ergodic theorem — historically the first operator ergodic theorem — and its generalizations), in the uniform operator topology (uniform ergodic theorems, see [HP], [DS], [N]), while if 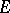 is a function space on a measure space, then also in the sense of almost-everywhere convergence of the means
is a function space on a measure space, then also in the sense of almost-everywhere convergence of the means 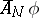 , etc., where
, etc., where 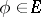 (individual ergodic theorems, i.e. the Birkhoff ergodic theorem and its generalizations; see, for example, the Ornstein–Chacon ergodic theorem; these are not always called operator ergodic theorems, however). Some operator ergodic theorems compare the force of various of the above-mentioned variants with each other, establishing that, from the existence of limits of means in one sense, it follows that limits exist in another sense [HP]. Some theorems speak not of the limit of means, but of the limit of the ratios of two means (e.g. the Ornstein–Chacon theorem).
(individual ergodic theorems, i.e. the Birkhoff ergodic theorem and its generalizations; see, for example, the Ornstein–Chacon ergodic theorem; these are not always called operator ergodic theorems, however). Some operator ergodic theorems compare the force of various of the above-mentioned variants with each other, establishing that, from the existence of limits of means in one sense, it follows that limits exist in another sense [HP]. Some theorems speak not of the limit of means, but of the limit of the ratios of two means (e.g. the Ornstein–Chacon theorem).
There are also operator ergodic theorems for  -parameter and even more general semi-groups.
-parameter and even more general semi-groups.
References
| [HP] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) MR0089373 Zbl 0392.46001 Zbl 0033.06501 |
| [DS] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Wiley (1988) MR1009164 MR1009163 MR1009162 |
| [N] | J. Neveu, "Mathematical foundations of the calculus of probabilities" , Holden-Day (1965) (Translated from French) MR0198505 |
| [VY] | A.M. Vershik, S.A. Yuzvinskii, "Dynamical systems with invariant measure" Progress in Math. , 8 (1970) pp. 151–215 Itogi Nauk. Mat. Anal. , 967 (1969) pp. 133–187 MR0286981 Zbl 0252.28006 |
| [KSS] | A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 : 2 (1977) pp. 974–1041 Itogi Nauk. i Tekhn. Mat. Anal. , 13 (1975) pp. 129–262 MR0584389 Zbl 0399.28011 |
| [K] | U. Krengel, "Recent progress in ergodic theorems" Astérisque , 50 (1977) pp. 151–192 MR486418 |
| [K2] | U. Krengel, "Ergodic theorems" , de Gruyter (1985) MR0797411 Zbl 0575.28009 |
Operator ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator_ergodic_theorem&oldid=23641