Difference between revisions of "Weil algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Ch. Ehresmann, "Les prolongements d'une variété différentiable. I. Calcul des jets, prolongement principal. II. L'espace des jets d'ordre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120050/w12005070.png" /> de <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120050/w12005071.png" /> dans <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w120/w120050/w12005072.png" />. III. Transitivité des prolongements" ''C.R. Acad. Sci. Paris'' , '''233''' (1951) pp. 598–600; 777–779; 1081–1083 {{MR|0045436}} {{MR|0045435}} {{MR|0044198}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I. Kolář, P.W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) {{MR|1202431}} {{ZBL|1084.53001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Weil, "Théorie des points proches sur les variétés differentielles" ''Colloq. Internat. Centre Nat. Rech. Sci.'' , '''52''' (1953) pp. 111–117</TD></TR></table> |
Revision as of 21:57, 30 March 2012
Motivated by algebraic geometry, A. Weil [a3] suggested the treatment of infinitesimal objects as homomorphisms from algebras of smooth functions 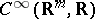 into some real finite-dimensional commutative algebra
into some real finite-dimensional commutative algebra 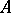 with unit. The points in
with unit. The points in 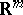 correspond to the choice
correspond to the choice 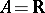 , while the algebra
, while the algebra  ,
, 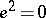 , of dual numbers (also called Study numbers) leads to the tangent vectors at points in
, of dual numbers (also called Study numbers) leads to the tangent vectors at points in 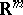 (viewed as derivations on functions). At the same time, Ch. Ehresmann established similar objects, jets (cf. also Jet), in the realm of differential geometry, cf. [a1].
(viewed as derivations on functions). At the same time, Ch. Ehresmann established similar objects, jets (cf. also Jet), in the realm of differential geometry, cf. [a1].
Since 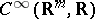 is formally real (i.e.
is formally real (i.e. 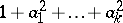 is invertible for all
is invertible for all 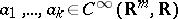 ), the values of the homomorphisms in
), the values of the homomorphisms in 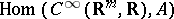 are in formally real subalgebras. Now, for each finite-dimensional real commutative unital algebra
are in formally real subalgebras. Now, for each finite-dimensional real commutative unital algebra 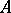 which is formally real, there is a decomposition of the unit
which is formally real, there is a decomposition of the unit  into all minimal idempotent elements. Thus,
into all minimal idempotent elements. Thus, 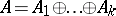 , where
, where  , and
, and 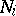 are nilpotent ideals in
are nilpotent ideals in 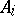 . A real unital finite-dimensional commutative algebra
. A real unital finite-dimensional commutative algebra 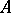 is called a Weil algebra if it is of the form
is called a Weil algebra if it is of the form
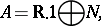 |
where 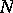 is the ideal of all nilpotent elements in
is the ideal of all nilpotent elements in 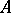 . The smallest
. The smallest 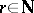 with the property
with the property 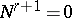 is called the depth, or order, of
is called the depth, or order, of 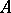 .
.
In other words, one may also characterize the Weil algebras as the formally real and local (i.e. the ring structure is local, cf. also Local ring) finite-dimensional commutative real unital algebras. See [a2], 35.1, for details.
As a consequence of the Nakayama lemma, the Weil algebras can be also characterized as the local finite-dimensional quotients of the algebras of real polynomials 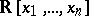 . Consequently, the Weil algebras
. Consequently, the Weil algebras 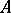 correspond to choices of ideals
correspond to choices of ideals 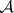 in
in 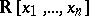 of finite codimension. The algebra of Study numbers
of finite codimension. The algebra of Study numbers 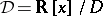 is given by
is given by 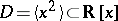 , for example. Equivalently, one may consider the algebras of formal power series or the algebras of germs of smooth functions at the origin
, for example. Equivalently, one may consider the algebras of formal power series or the algebras of germs of smooth functions at the origin 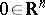 (cf. also Germ) instead of the polynomials.
(cf. also Germ) instead of the polynomials.
The width of a Weil algebra 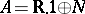 is defined as the dimension of the vector space
is defined as the dimension of the vector space  . If
. If 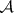 is an ideal of finite codimension in
is an ideal of finite codimension in 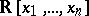 ,
, 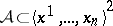 , then the width of
, then the width of 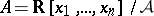 equals
equals  . For example, the Weil algebra
. For example, the Weil algebra
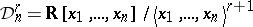 |
has width  and order
and order  , and it coincides with the algebra
, and it coincides with the algebra 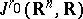 of
of  -jets of smooth functions at the origin in
-jets of smooth functions at the origin in 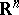 . Moreover, each Weil algebra of width
. Moreover, each Weil algebra of width  and order
and order  is a quotient of
is a quotient of 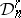 .
.
Tensor products of Weil algebras are Weil algebras again. For instance,  .
.
The infinitesimal objects of type 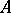 attached to points in
attached to points in 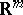 are simply
are simply 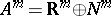 . All smooth functions
. All smooth functions 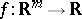 extend to
extend to 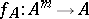 by the evaluation of the Taylor series (cf. also Whitney extension theorem)
by the evaluation of the Taylor series (cf. also Whitney extension theorem)
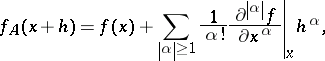 |
where 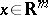 ,
, 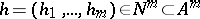 ,
, 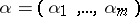 are multi-indices,
are multi-indices, 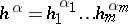 . Applying this formula to all components of a mapping
. Applying this formula to all components of a mapping 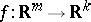 , one obtains an assignment functorial in both
, one obtains an assignment functorial in both 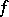 and
and 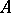 . Of course, this definition extends to a functor on all locally defined smooth mappings
. Of course, this definition extends to a functor on all locally defined smooth mappings 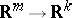 and so each Weil algebra gives rise to a Weil functor
and so each Weil algebra gives rise to a Weil functor 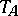 . (See Weil bundle for more details.)
. (See Weil bundle for more details.)
The automorphism group  of a Weil algebra is a Lie subgroup (cf. also Lie group) in
of a Weil algebra is a Lie subgroup (cf. also Lie group) in 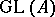 and its Lie algebra coincides with the space of all derivations (cf. also Derivation in a ring) on
and its Lie algebra coincides with the space of all derivations (cf. also Derivation in a ring) on 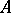 ,
, 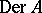 , i.e. all mappings
, i.e. all mappings 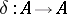 satisfying
satisfying 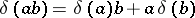 , cf. [a2], 42.9.
, cf. [a2], 42.9.
References
| [a1] | Ch. Ehresmann, "Les prolongements d'une variété différentiable. I. Calcul des jets, prolongement principal. II. L'espace des jets d'ordre  de de 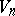 dans dans  . III. Transitivité des prolongements" C.R. Acad. Sci. Paris , 233 (1951) pp. 598–600; 777–779; 1081–1083 MR0045436 MR0045435 MR0044198 . III. Transitivité des prolongements" C.R. Acad. Sci. Paris , 233 (1951) pp. 598–600; 777–779; 1081–1083 MR0045436 MR0045435 MR0044198 |
| [a2] | I. Kolář, P.W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) MR1202431 Zbl 1084.53001 |
| [a3] | A. Weil, "Théorie des points proches sur les variétés differentielles" Colloq. Internat. Centre Nat. Rech. Sci. , 52 (1953) pp. 111–117 |
Weil algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_algebra&oldid=18951