Difference between revisions of "Baxter algebra"
(Importing text file) |
(TeX partially done) |
||
| Line 1: | Line 1: | ||
| − | Baxter algebras originated in the following problem in fluctuation theory: Find the distribution functions of the maxima | + | Baxter algebras originated in the following problem in fluctuation theory: Find the distribution functions of the maxima $\max\{0, S_1, \ldots, S_n \}$ of the partial sums $S_0 = 0$, $S_1=X_1$, $S_2=X_1 + X+2$, $\ldots$, $S_n = X_1+\cdots+X_n$, of a sequence $X_i$ of independent identically-distributed random variables (cf. also [[Random variable|Random variable]]). A central result in this area is the ''Spitzer identity'' |
| + | $$ | ||
| + | \sum_{n=0}^\infty \phi_n(t) \lambda^n = \exp\left[{ \psi_k(t) \frac{\lambda^k}{k} }\right]\ , | ||
| + | $$ | ||
| + | where $\phi_n(t)$ is the characteristic function of $\max\{0, S_1, \ldots, S_n \}$ and $\psi_k(t)$ is the characteristic function of $\max\{0, S_k \}$. Spitzer's identity bears an uncanny resemblance to the ''Waring identity'' | ||
| + | $$ | ||
| + | \sum_{n=0}^\infty e_n(x_1,x_2,\ldots) \lambda^n = \exp\left[{ -\sum_{k=1}^\infty (-1)^k p_k(x_1,x_2,\ldots) \frac{\lambda^k}{k} }\right] | ||
| + | $$ | ||
| + | where $e_n(x_1,x_2,\ldots)$ are [[elementary symmetric function]]s and $p_k(x_1,x_2,\ldots)$ are power sum symmetric functions. The algebraic structure underlying both identities is a Baxter algebra. These algebras were defined by G.-C. Rota in [[#References|[a2]]], [[#References|[a3]]]. | ||
| − | + | A Baxter operator $P$ on an [[algebra]] $A$ over a field $k$ is a [[linear operator]] from $A$ to itself satisfying the identity | |
| + | $$\label{eq:a1} | ||
| + | P(xPy) + P(yPx) = (Px)(Py) + q P(xy) | ||
| + | $$ | ||
| − | where | + | where $q$ is a constant in $k$. A '''Baxter algebra''' is an algebra with a Baxter operator. |
| − | + | An example is the algebra of real-valued continuous functions on the interval $[0,1]$ with the integration operator | |
| + | $$ | ||
| + | PF(x) = \int_0^x f(t) dt \ . | ||
| + | $$ | ||
| − | + | The formula for [[integration by parts]] is identity (a1) with $q=0$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The formula for [[ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Another example is the [[Banach algebra]] of characteristic functions of distribution functions of random variables (cf. also [[Characteristic function]]; [[Random variable]]) with the Baxter operator $P$ which sends the characteristic function of a random variable $X$ to the characteristic function of $\max\{0,X\}$. That is, if | ||
| + | $$ | ||
| + | \xi(t) = \int_{-\infty}^\infty \exp(itx) dF(x) | ||
| + | $$ | ||
then | then | ||
| + | $$\label{eq:a2} | ||
| + | P\xi(t) = \int_0^\infty \exp(itx) dF(x) \ . | ||
| + | $$ | ||
| − | + | Given any [[endomorphism]] $E$ (that is, a linear operator satisfying $E(xy) = E(x)E(y)$) on an algebra $A$, the operator | |
| − | + | $$ | |
| − | Given any [[ | + | P = E + E^2 + \cdots = E(I-E)^{-1} |
| − | + | $$ | |
| − | + | is a Baxter operator if the infinite series converges. In particular, the $q$-integral | |
| − | + | $$ | |
| − | is a Baxter operator if the infinite series converges. In particular, the | + | Pf(t) = f(qt) + f(q^2t) + f(q^3t) + \cdots |
| − | + | $$ | |
| − | |||
| − | |||
is a Baxter operator. | is a Baxter operator. | ||
| − | The standard Baxter algebra over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008037.png" /> with generators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008038.png" /> is defined in the following way. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008039.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008040.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008041.png" /> be sequences such that the terms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008042.png" /> are algebraically independent. On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008043.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008044.png" /> with coordinate-wise addition and multiplication generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008045.png" />, define the Baxter operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008046.png" /> by | + | The ''standard Baxter algebra'' over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008037.png" /> with generators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008038.png" /> is defined in the following way. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008039.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008040.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008041.png" /> be sequences such that the terms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008042.png" /> are algebraically independent. On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008043.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008044.png" /> with coordinate-wise addition and multiplication generated by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008045.png" />, define the Baxter operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008046.png" /> by |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008047.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130080/b13008047.png" /></td> </tr></table> | ||
| Line 58: | Line 59: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Baxter, "An analytic problem whose solution follows from a simple algebraic identity" ''Pacific J. Math.'' , '''10''' (1960) pp. 731–742</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.-C. Rota, "Baxter algebras and combinatorial identities I–II" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 325–334</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.-C. Rota, "Baxter algebras: an introduction" J.P.S. Kung (ed.) , ''Gian-Carlo Rota on Combinatorics'' , Birkhäuser (1995) pp. 504–512</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Baxter, "An analytic problem whose solution follows from a simple algebraic identity" ''Pacific J. Math.'' , '''10''' (1960) pp. 731–742</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> G.-C. Rota, "Baxter algebras and combinatorial identities I–II" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 325–334</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> G.-C. Rota, "Baxter algebras: an introduction" J.P.S. Kung (ed.) , ''Gian-Carlo Rota on Combinatorics'' , Birkhäuser (1995) pp. 504–512</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | [[Category:TeX partially done]] | ||
Revision as of 11:16, 28 November 2015
Baxter algebras originated in the following problem in fluctuation theory: Find the distribution functions of the maxima $\max\{0, S_1, \ldots, S_n \}$ of the partial sums $S_0 = 0$, $S_1=X_1$, $S_2=X_1 + X+2$, $\ldots$, $S_n = X_1+\cdots+X_n$, of a sequence $X_i$ of independent identically-distributed random variables (cf. also Random variable). A central result in this area is the Spitzer identity $$ \sum_{n=0}^\infty \phi_n(t) \lambda^n = \exp\left[{ \psi_k(t) \frac{\lambda^k}{k} }\right]\ , $$ where $\phi_n(t)$ is the characteristic function of $\max\{0, S_1, \ldots, S_n \}$ and $\psi_k(t)$ is the characteristic function of $\max\{0, S_k \}$. Spitzer's identity bears an uncanny resemblance to the Waring identity $$ \sum_{n=0}^\infty e_n(x_1,x_2,\ldots) \lambda^n = \exp\left[{ -\sum_{k=1}^\infty (-1)^k p_k(x_1,x_2,\ldots) \frac{\lambda^k}{k} }\right] $$ where $e_n(x_1,x_2,\ldots)$ are elementary symmetric functions and $p_k(x_1,x_2,\ldots)$ are power sum symmetric functions. The algebraic structure underlying both identities is a Baxter algebra. These algebras were defined by G.-C. Rota in [a2], [a3].
A Baxter operator $P$ on an algebra $A$ over a field $k$ is a linear operator from $A$ to itself satisfying the identity $$\label{eq:a1} P(xPy) + P(yPx) = (Px)(Py) + q P(xy) $$
where $q$ is a constant in $k$. A Baxter algebra is an algebra with a Baxter operator.
An example is the algebra of real-valued continuous functions on the interval $[0,1]$ with the integration operator $$ PF(x) = \int_0^x f(t) dt \ . $$
The formula for integration by parts is identity (a1) with $q=0$.
Another example is the Banach algebra of characteristic functions of distribution functions of random variables (cf. also Characteristic function; Random variable) with the Baxter operator $P$ which sends the characteristic function of a random variable $X$ to the characteristic function of $\max\{0,X\}$. That is, if $$ \xi(t) = \int_{-\infty}^\infty \exp(itx) dF(x) $$ then $$\label{eq:a2} P\xi(t) = \int_0^\infty \exp(itx) dF(x) \ . $$
Given any endomorphism $E$ (that is, a linear operator satisfying $E(xy) = E(x)E(y)$) on an algebra $A$, the operator $$ P = E + E^2 + \cdots = E(I-E)^{-1} $$ is a Baxter operator if the infinite series converges. In particular, the $q$-integral $$ Pf(t) = f(qt) + f(q^2t) + f(q^3t) + \cdots $$ is a Baxter operator.
The standard Baxter algebra over a field 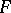 with generators
with generators 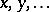 is defined in the following way. Let
is defined in the following way. Let 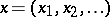 ,
, 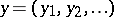 ,
, 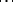 be sequences such that the terms
be sequences such that the terms 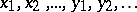 are algebraically independent. On the
are algebraically independent. On the 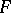 -algebra
-algebra 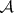 with coordinate-wise addition and multiplication generated by
with coordinate-wise addition and multiplication generated by 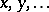 , define the Baxter operator
, define the Baxter operator 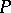 by
by
 |
The standard Baxter algebra 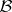 is the smallest subalgebra of
is the smallest subalgebra of 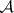 containing
containing 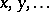 and closed under
and closed under 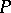 . Rota [a2], [a3] proved that the standard Baxter algebra is free in the category of Baxter algebras (cf. also Free algebra).
. Rota [a2], [a3] proved that the standard Baxter algebra is free in the category of Baxter algebras (cf. also Free algebra).
If  is the sequence
is the sequence 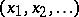 , then the
, then the 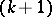 st term in
st term in 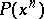 is the power sum symmetric function
is the power sum symmetric function 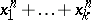 and the
and the 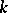 th term in
th term in 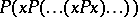 , where there are
, where there are  occurrences of
occurrences of 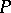 , is
, is 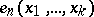 . Hence, the free Baxter algebra on one generator
. Hence, the free Baxter algebra on one generator  is isomorphic to the algebra of symmetric functions (cf. also Symmetric function). Because the elementary symmetric functions are algebraically independent, the free Baxter algebra in one generator
is isomorphic to the algebra of symmetric functions (cf. also Symmetric function). Because the elementary symmetric functions are algebraically independent, the free Baxter algebra in one generator  is isomorphic to the algebra of polynomials in the variables
is isomorphic to the algebra of polynomials in the variables  . This solves the word problem (cf. also Identity problem) for Baxter algebras with one generator. The word problem for Baxter algebras with more than one generator is solved in a similar way by P. Cartier. In particular, an identity amongst symmetric functions can be translated into an identity satisfied by all Baxter algebras on one generator. For example, writing Waring's identity in terms of Baxter operators, one obtains
. This solves the word problem (cf. also Identity problem) for Baxter algebras with one generator. The word problem for Baxter algebras with more than one generator is solved in a similar way by P. Cartier. In particular, an identity amongst symmetric functions can be translated into an identity satisfied by all Baxter algebras on one generator. For example, writing Waring's identity in terms of Baxter operators, one obtains
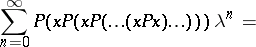 |
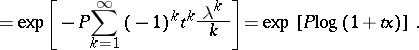 |
When 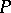 is the Baxter operator given in (a2), this identity is Spitzer's identity. When
is the Baxter operator given in (a2), this identity is Spitzer's identity. When 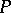 is the
is the 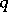 -integral, this identity becomes the Eulerian identity
-integral, this identity becomes the Eulerian identity
 |
References
| [a1] | G. Baxter, "An analytic problem whose solution follows from a simple algebraic identity" Pacific J. Math. , 10 (1960) pp. 731–742 |
| [a2] | G.-C. Rota, "Baxter algebras and combinatorial identities I–II" Bull. Amer. Math. Soc. , 75 (1969) pp. 325–334 |
| [a3] | G.-C. Rota, "Baxter algebras: an introduction" J.P.S. Kung (ed.) , Gian-Carlo Rota on Combinatorics , Birkhäuser (1995) pp. 504–512 |
Baxter algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baxter_algebra&oldid=18813