Difference between revisions of "Braided category"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 158 formulas out of 186 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 186 formulas, 158 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''braided monoidal category, quasi-tensor category'' | ''braided monoidal category, quasi-tensor category'' | ||
| − | A generalization of the notion of tensor product of vector spaces, in which | + | A generalization of the notion of tensor product of vector spaces, in which $\otimes$ is associative only up to isomorphism and the transposition isomorphism $\otimes \rightarrow \otimes ^ { \text{op} }$ need not square to the identity. |
| − | The full definition is: a [[Category|category]] | + | The full definition is: a [[Category|category]] $\mathcal{C}$ of objects $V$, $W$, $Z$, etc., equipped with a functor $\otimes : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C}$, and a collection of functorial isomorphisms |
| − | + | \begin{equation*} \Phi _ { V , W , Z } : ( V \bigotimes W ) \bigotimes Z \rightarrow V \bigotimes ( W \bigotimes Z ) \end{equation*} | |
(called the associator) between any three objects and | (called the associator) between any three objects and | ||
| − | + | \begin{equation*} \Psi _ { V , W } : V \bigotimes W \rightarrow W \bigotimes V \end{equation*} | |
(called the braiding) between any two objects. "Functorial" means that these isomorphisms commute with any morphisms between objects. Thus, | (called the braiding) between any two objects. "Functorial" means that these isomorphisms commute with any morphisms between objects. Thus, | ||
| − | + | \begin{equation*} ( \phi \bigotimes \text { id } ) \Psi _ { V , W } = \Psi _ { V , Z } ( \text { id } \bigotimes \phi ) , \forall \phi : W \rightarrow Z, \end{equation*} | |
| − | if the morphism is applied before or after the braiding. Similarly for functoriality in the other arguments of | + | if the morphism is applied before or after the braiding. Similarly for functoriality in the other arguments of $\Psi$ and in the arguments of $\Phi$. The precise definition is that $\Phi : ( \otimes ) \otimes \rightarrow \otimes ( \otimes )$ and $\Psi : \otimes \rightarrow \otimes ^ { \text{ op} }$ are natural equivalences, where $( \otimes ) \otimes :\mathcal C \times \mathcal C \times \mathcal C \rightarrow \mathcal C$ is the functor sending $( V , W , Z )$ to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042017.png"/>, etc., and $\otimes ^{\operatorname{op}} : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C}$ is the functor sending $( V , W )$ to $W \otimes V$. |
| − | In addition, these functors are required to be coherent. The coherence for | + | In addition, these functors are required to be coherent. The coherence for $\Phi$ is the pentagon identity |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/b120420a.gif" style="border:1px solid;"/> |
Figure: b120420a | Figure: b120420a | ||
| − | It says that the two ways to reverse the bracketings as shown coincide. MacLane's coherence theorem says that then all other routes between two bracketed tensor products also coincide. In effect, this means that one may generalize constructions in linear algebra exactly as if | + | It says that the two ways to reverse the bracketings as shown coincide. MacLane's coherence theorem says that then all other routes between two bracketed tensor products also coincide. In effect, this means that one may generalize constructions in linear algebra exactly as if $\otimes$ were strictly associative, dropping brackets. Afterwards one may add brackets, for example with brackets accumulating to the left, and then insert applications of $\Phi$ as needed for the desired compositions to make sense; all different ways to do this will yield the same net result. |
| − | One also requires a unit object | + | One also requires a unit object $1$ and an associated collection of functorial isomorphisms $r _{V} : V \rightarrow V \otimes \underline { 1 }$ and $l _ { V } : V \rightarrow \underline { 1 } \otimes V$ obeying a triangle coherence identity |
| − | + | \begin{equation*} \operatorname { id} \bigotimes r _ { W } = \Phi _ { V , 1 , W } \circ ( l _ { V } \bigotimes \text { id } ). \end{equation*} | |
| − | This structure | + | This structure $( \mathcal C , \otimes , \Phi , \underline { 1 } , l , r )$ is called a monoidal category (see also [[Triple|Triple]]). |
| − | The coherence conditions for the additional structure | + | The coherence conditions for the additional structure $\Psi$ of a braided category are the so-called hexagon identities |
| − | + | \begin{equation*} \Psi _ { V \bigotimes W , Z } = \Psi _ { V , Z } \circ \Psi _ { W , Z }, \end{equation*} | |
| − | + | \begin{equation*} \Psi _ { V , W \bigotimes Z } = \Psi _ { V ,\, Z } \circ \Psi _ { V , W } . \end{equation*} | |
| − | Here and below, the bracketings and | + | Here and below, the bracketings and $\Phi$ needed to make sense of these identities are omitted. (When they are inserted, each identity corresponds to a diagram with six arrows.) One can show that compatibility of $\Psi$ with $1$ is then automatic. |
| − | Notice that although | + | Notice that although $\Psi$ generalizes the concept of transposition of vector spaces, one does not demand that $\Psi _ { V , W } = \Psi _ { W , V } ^ { - 1 }$. If this does hold for all $V$, $W$, then a symmetric monoidal category or tensor category is obtained. In this case the two hexagon identities are equivalent and ensure that all ways to go |
| − | + | \begin{equation*} V _ { 1 } \bigotimes \ldots \bigotimes V _ { n } \rightarrow V _ { \sigma ( 1 ) } \bigotimes \ldots \bigotimes V _ { \sigma ( n ) } \end{equation*} | |
| − | ( | + | ($\sigma$ a permutation) by composing $\Psi$ (and $\Phi$) yield the same result. In particular, there is an action of the [[Symmetric group|symmetric group]] $S _ { n }$ in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042044.png"/> for any object $V$. |
| − | For a general braided category there is a similar result in terms of braids. To explain this, the following notational device is used: instead of writing the morphisms | + | For a general braided category there is a similar result in terms of braids. To explain this, the following notational device is used: instead of writing the morphisms $\Psi _ { V , W }$ and $\Psi _ { W , V } ^ { - 1 }$ in the usual way as arrows, one writes them as braids and assumes that they point downwards: |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/b120420b.gif" style="border:1px solid;"/> |
Figure: b120420b | Figure: b120420b | ||
| − | One writes another morphism | + | One writes another morphism $\phi : W \rightarrow Z$, say, as a node on a strand connecting $W$ to $Z$ and assumed to be pointing downwards. Functoriality says that morphisms can be pulled through braid crossings as |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/b120420c.gif" style="border:1px solid;"/> |
Figure: b120420c | Figure: b120420c | ||
| Line 59: | Line 67: | ||
Similarly for morphisms on the other strand. When the tensor product of several morphisms is applied, one writes their strands separately side by side, connecting the relevant objects in the tensor product. On the other hand, one is free to group some of the objects in the tensor product together as a single object and represent morphisms to and from it by a single strand. This notation is consistent precisely because of the hexagon conditions, which become | Similarly for morphisms on the other strand. When the tensor product of several morphisms is applied, one writes their strands separately side by side, connecting the relevant objects in the tensor product. On the other hand, one is free to group some of the objects in the tensor product together as a single object and represent morphisms to and from it by a single strand. This notation is consistent precisely because of the hexagon conditions, which become | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/b120420d.gif" style="border:1px solid;"/> |
Figure: b120420d | Figure: b120420d | ||
| Line 65: | Line 73: | ||
The doubled strands on the left-hand side could be replaced by single strands for the composite morphisms. | The doubled strands on the left-hand side could be replaced by single strands for the composite morphisms. | ||
| − | The coherence theorem for braided categories then asserts that different routes between tensor product expressions by repeated applications of | + | The coherence theorem for braided categories then asserts that different routes between tensor product expressions by repeated applications of $\Phi$, $\Psi$ and their inverses compose to the same morphism if the corresponding braids are the same. In particular, for any object $V$ there is an action of the pure braid group $B _ { n }$ on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042055.png"/>. The former can be presented as |
| − | + | \begin{equation*} b _ { i } b _ { i + 1} b _ { i } = b _ { i + 1} b _ { i } b _ { i } + 1 , b _ { i } b _ { j } = b _ { j } b _ { i } , \quad | i - j | \geq 2, \end{equation*} | |
| − | where | + | where $b _ { i }$ is represented by $\Psi$ acting in the $( i , i + 1 )$th copies of $V$. The representation usually has a kernel and $B _ { n }$ modulo this kernel is the Hecke algebra associated to an object in a braided category. |
| − | Finally, an object | + | Finally, an object $V$ in a braided category is rigid if there are another object $V ^ { * }$ and morphisms $\operatorname{ev} _ { V } : V ^ { * } \otimes V \rightarrow \underline { 1 }$ and $\operatorname{coev}_V : \underline { 1 } \rightarrow V \otimes V ^ { * }$ such that |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042066.png"/></td> </tr></table> |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042067.png"/></td> </tr></table> |
| − | (suppressing | + | (suppressing $\Phi$, $l$, $r$). Here, $V ^ { * }$ is called a left dual of $V$ and is unique up to isomorphism (there is a similar notion of right dual). $\mathcal{C}$ is called rigid if every object has such duals. Using diagrammatic notation one writes |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/b120420e.gif" style="border:1px solid;"/> |
Figure: b120420e | Figure: b120420e | ||
| Line 85: | Line 93: | ||
and the above axioms become | and the above axioms become | ||
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/b120420f.gif" style="border:1px solid;"/> |
Figure: b120420f | Figure: b120420f | ||
| − | Note that in a rigid braided category, morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042074.png" /> look like knots (cf. also [[Knot theory|Knot theory]]; [[Braid theory|Braid theory]]). Every knot presented on paper is in fact the closure of some braid, so with a little more structure (notably, both left and right duals) one can arrange that every oriented knot can be read from top to bottom as a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042075.png" />. Fixing an object | + | Note that in a rigid braided category, morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042074.png"/> look like knots (cf. also [[Knot theory|Knot theory]]; [[Braid theory|Braid theory]]). Every knot presented on paper is in fact the closure of some braid, so with a little more structure (notably, both left and right duals) one can arrange that every oriented knot can be read from top to bottom as a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042075.png"/>. Fixing an object $V$, |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/" style="border:1px solid;"/> |
| − | can be read as a left or right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042077.png" /> and | + | can be read as a left or right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042077.png"/> and |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/" style="border:1px solid;"/> |
| − | can be read as a left or right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042078.png" /> (in accordance with orientation). One can read braid crossings as | + | can be read as a left or right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042078.png"/> (in accordance with orientation). One can read braid crossings as $\Psi$ or $\Psi ^ { - 1 }$. The result is not quite a knot invariant but can usually be adjusted to become one. |
==Examples.== | ==Examples.== | ||
| − | Some standard examples of braided categories are provided by the following constructions over a ground field | + | Some standard examples of braided categories are provided by the following constructions over a ground field $k$. Its invertible elements are denoted $k ^ { * }$. |
| − | 1) Fix | + | 1) Fix $q \in k$, an $n$th root of unity. The category of anyspaces $\operatorname{Vec}_n$ consists of $\mathbf{Z} / n \mathbf{Z}$-graded vector spaces $V = \oplus _ { i = 0 } ^ { n - 1 } V _ { i }$ (where the elements of $V _ { i }$ have degree $i$). Morphisms are degree-preserving linear mappings. One takes the associator trivial and the braiding |
| − | + | \begin{equation*} \Psi _ { V , W } ( v \bigotimes w ) = q ^ { |v| | w | } w \bigotimes v \end{equation*} | |
| − | for | + | for $v \in V$ and $w \in W$ of degree $v$, $w $, respectively. |
| − | Clearly, | + | Clearly, $\operatorname{Vec}_{1}$ is the usual category of vector spaces, while $\text{Vec}_2$ is the category of linear superspaces or ${\bf Z} / 2 {\bf Z}$-graded vector spaces. The category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b12042098.png"/> of $\mathbf{Z}$-graded spaces is braided similarly for any $q \in k ^ { * }$. |
| − | A similar construction works for grading by any Abelian group | + | A similar construction works for grading by any Abelian group $G$ equipped with a bicharacter $\beta : G \times G \rightarrow k ^ { * }$ (a function multiplicative in each argument) and braiding |
| − | + | \begin{equation*} \Psi _ { V , W } ( v \bigotimes w ) = \beta ( | v | , | w | ) w \bigotimes v \end{equation*} | |
| − | on elements of degree | + | on elements of degree $| v | , | w | \in G$. |
| − | 2) If | + | 2) If $G$ is a group and $\phi : G \times G \times G \rightarrow k ^ { * }$ a group $3$-cocycle, then the category of $G$-graded spaces is monoidal with associator |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b120420109.png"/></td> </tr></table> |
| − | on elements of degree | + | on elements of degree $| v | , | w | , | z | \in G$. If $G$ is Abelian and equipped with a quasi-bicharacter with respect to $\phi$, then the category is braided. |
| − | For example, the octonion algebra lives naturally in such a category with | + | For example, the octonion algebra lives naturally in such a category with $G = \mathbf{Z} _ { 2 } \times \mathbf{Z} _ { 2 } \times \mathbf{Z} _ { 2 }$ and $\phi$ a certain coboundary. |
| − | 3) The category of finite-dimensional representations of the quantum enveloping algebras (cf. also [[Quantum groups|Quantum groups]]; [[Universal enveloping algebra|Universal enveloping algebra]]) | + | 3) The category of finite-dimensional representations of the quantum enveloping algebras (cf. also [[Quantum groups|Quantum groups]]; [[Universal enveloping algebra|Universal enveloping algebra]]) $U _ { q } ( \mathfrak { g } )$ associated to a semi-simple [[Lie algebra|Lie algebra]] $\frak g$. Also, certain classes of infinite-dimensional representations. Associated to the standard representation of $U _ { q } ( \operatorname{sl} _ { 2 } )$ is the standard Hecke algebra defined by the additional relation $( b _ { i } - q ) ( b _ { i } + q ^ { - 1 } ) = 0$. The knot invariant associated to this same representation is the Jones knot polynomial. |
| − | In an algebraic formulation, if | + | In an algebraic formulation, if $H$, $\mathcal{R} \in H \otimes H$, is a [[Quasi-triangular Hopf algebra|quasi-triangular Hopf algebra]], then its category $\square _ { H } \cal M$ of representations is braided with $\Psi = \tau \circ \mathcal{R}$, where one first acts with the quasi-triangular structure $\mathcal{R} \in H \otimes H$ and then applies the usual transposition mapping $\tau$. |
| − | 4) The category of co-modules under the matrix quantum groups (cf. [[Quantum groups|Quantum groups]]) | + | 4) The category of co-modules under the matrix quantum groups (cf. [[Quantum groups|Quantum groups]]) $G_q$. For example, the quantum plane generated by $x , y$ modulo the relations $y x = q x y$ is covariant under $\operatorname{SL} _ { q } ( 2 )$ and hence lives as an algebra in its braided category of co-modules. Likewise, the category of co-modules under a quantum matrix bi-algebra $A ( R )$ associated to an invertible solution $R$ of the [[Yang–Baxter equation|Yang–Baxter equation]] is braided. |
| − | In a general algebraic formulation, if | + | In a general algebraic formulation, if $H$, $\mathcal{R} : H \otimes H \rightarrow k $, is a dual (or co-) quasi-triangular Hopf algebra, then its category of co-modules is braided by |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b120420133.png"/></td> </tr></table> |
| − | where | + | where $\sum _ { V } v ^ { \overline{( 1 ) }} \otimes v ^ { \overline{( 2 ) } }$ denotes the result of the co-action $V \rightarrow H \otimes V$. |
| − | 5) If | + | 5) If $H$ is any [[Hopf algebra|Hopf algebra]] with invertible antipode, then its category $\square _ { H } ^ { H } \mathcal{M}$ of crossed modules (also called Drinfel'd–Radford–Yetter modules) is braided. Here, objects are vector spaces $V$ which are both modules and co-modules under $H$, the two being compatible in the sense |
| − | + | \begin{equation*} \sum h_{ ( 1 )} v ^ { \overline{( 1 )} } \bigotimes h_{ ( 2 )} \rhd v ^ { \overline{( 2 )} } = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b120420141.png"/></td> </tr></table> |
| − | for | + | for $h \in H$ and $v \in V$, where $\triangleright$ denotes the action and $\sum h _ { ( 1 ) } \otimes h _ { ( 2 ) }$ denotes the co-product. The braiding is |
| − | + | \begin{equation*} \Psi _ { V , W } ( v \bigotimes w ) = \sum v ^ { \overline{( 1 )} } \rhd w \bigotimes v ^ { \overline{( 2 )} }. \end{equation*} | |
| − | For example, if | + | For example, if $\frak g$ is any Lie algebra and $U ( \mathfrak { g } )$ is its enveloping algebra (cf. also [[Universal enveloping algebra|Universal enveloping algebra]]), then $V = k 1 \oplus \mathfrak g \subset U ( \mathfrak g )$ is a crossed module by the adjoint action and the co-product of $U ( \mathfrak { g } )$. The braiding induced on it is |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120420/b120420151.png"/></td> </tr></table> |
| − | 6) Let | + | 6) Let $\mathcal{C}$ be any monoidal category. Then its representation-theoretic dual category $\mathcal{C} ^ { \circ }$ (also called the double $D ( \mathcal{C} )$ or centre $Z (\cal C )$) is a braided category. Objects are pairs $( V , \lambda )$ where $V$ is an object of $\mathcal{C}$ and $\lambda _ { W } : V \otimes W \rightarrow W \otimes V$ is a collection of functorial isomorphisms representing the $\otimes$ of $\mathcal{C}$ in the sense |
| − | + | \begin{equation*} \lambda _ { \underline{1} } = \operatorname {id} , \lambda _ { W \bigotimes Z} = \lambda_{Z} \circ \lambda _ { W } \end{equation*} | |
| − | ( | + | ($\Phi$, $l$, $r$ suppressed in this notation). The braiding is $\Psi _ { ( V , \lambda ) , ( W , \mu ) } = \lambda _ { W }$. |
| − | These constructions are in roughly increasing order of generality. Thus, the categorical dual or double construction applied to the category of | + | These constructions are in roughly increasing order of generality. Thus, the categorical dual or double construction applied to the category of $H$-modules yields the category of crossed modules $\square _ { H } ^ { H } \mathcal{M}$. These, in turn, are an elementary reformulation (and thereby a slight generalization to infinite-dimensional $H$) of the category of $D ( H )$-modules, where $D ( H )$ is the quantum double quasi-triangular Hopf algebra associated to any finite-dimensional Hopf algebra $H$. Meanwhile, a bicharacter on an Abelian group extends by linearity to a dual-quasi-triangular structure on the corresponding group algebra. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> S. MacLane, "Categories for the working mathematician" , ''GTM'' , '''5''' , Springer (1974)</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Joyal, R. Street, "Braided monoidal categories" ''Math. Reports Macquarie Univ.'' , '''86008''' (1986)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995)</td></tr></table> |
Revision as of 17:02, 1 July 2020
braided monoidal category, quasi-tensor category
A generalization of the notion of tensor product of vector spaces, in which $\otimes$ is associative only up to isomorphism and the transposition isomorphism $\otimes \rightarrow \otimes ^ { \text{op} }$ need not square to the identity.
The full definition is: a category $\mathcal{C}$ of objects $V$, $W$, $Z$, etc., equipped with a functor $\otimes : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C}$, and a collection of functorial isomorphisms
\begin{equation*} \Phi _ { V , W , Z } : ( V \bigotimes W ) \bigotimes Z \rightarrow V \bigotimes ( W \bigotimes Z ) \end{equation*}
(called the associator) between any three objects and
\begin{equation*} \Psi _ { V , W } : V \bigotimes W \rightarrow W \bigotimes V \end{equation*}
(called the braiding) between any two objects. "Functorial" means that these isomorphisms commute with any morphisms between objects. Thus,
\begin{equation*} ( \phi \bigotimes \text { id } ) \Psi _ { V , W } = \Psi _ { V , Z } ( \text { id } \bigotimes \phi ) , \forall \phi : W \rightarrow Z, \end{equation*}
if the morphism is applied before or after the braiding. Similarly for functoriality in the other arguments of $\Psi$ and in the arguments of $\Phi$. The precise definition is that $\Phi : ( \otimes ) \otimes \rightarrow \otimes ( \otimes )$ and $\Psi : \otimes \rightarrow \otimes ^ { \text{ op} }$ are natural equivalences, where $( \otimes ) \otimes :\mathcal C \times \mathcal C \times \mathcal C \rightarrow \mathcal C$ is the functor sending $( V , W , Z )$ to 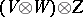 , etc., and $\otimes ^{\operatorname{op}} : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C}$ is the functor sending $( V , W )$ to $W \otimes V$.
, etc., and $\otimes ^{\operatorname{op}} : \mathcal{C} \times \mathcal{C} \rightarrow \mathcal{C}$ is the functor sending $( V , W )$ to $W \otimes V$.
In addition, these functors are required to be coherent. The coherence for $\Phi$ is the pentagon identity

Figure: b120420a
It says that the two ways to reverse the bracketings as shown coincide. MacLane's coherence theorem says that then all other routes between two bracketed tensor products also coincide. In effect, this means that one may generalize constructions in linear algebra exactly as if $\otimes$ were strictly associative, dropping brackets. Afterwards one may add brackets, for example with brackets accumulating to the left, and then insert applications of $\Phi$ as needed for the desired compositions to make sense; all different ways to do this will yield the same net result.
One also requires a unit object $1$ and an associated collection of functorial isomorphisms $r _{V} : V \rightarrow V \otimes \underline { 1 }$ and $l _ { V } : V \rightarrow \underline { 1 } \otimes V$ obeying a triangle coherence identity
\begin{equation*} \operatorname { id} \bigotimes r _ { W } = \Phi _ { V , 1 , W } \circ ( l _ { V } \bigotimes \text { id } ). \end{equation*}
This structure $( \mathcal C , \otimes , \Phi , \underline { 1 } , l , r )$ is called a monoidal category (see also Triple).
The coherence conditions for the additional structure $\Psi$ of a braided category are the so-called hexagon identities
\begin{equation*} \Psi _ { V \bigotimes W , Z } = \Psi _ { V , Z } \circ \Psi _ { W , Z }, \end{equation*}
\begin{equation*} \Psi _ { V , W \bigotimes Z } = \Psi _ { V ,\, Z } \circ \Psi _ { V , W } . \end{equation*}
Here and below, the bracketings and $\Phi$ needed to make sense of these identities are omitted. (When they are inserted, each identity corresponds to a diagram with six arrows.) One can show that compatibility of $\Psi$ with $1$ is then automatic.
Notice that although $\Psi$ generalizes the concept of transposition of vector spaces, one does not demand that $\Psi _ { V , W } = \Psi _ { W , V } ^ { - 1 }$. If this does hold for all $V$, $W$, then a symmetric monoidal category or tensor category is obtained. In this case the two hexagon identities are equivalent and ensure that all ways to go
\begin{equation*} V _ { 1 } \bigotimes \ldots \bigotimes V _ { n } \rightarrow V _ { \sigma ( 1 ) } \bigotimes \ldots \bigotimes V _ { \sigma ( n ) } \end{equation*}
($\sigma$ a permutation) by composing $\Psi$ (and $\Phi$) yield the same result. In particular, there is an action of the symmetric group $S _ { n }$ in 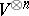 for any object $V$.
for any object $V$.
For a general braided category there is a similar result in terms of braids. To explain this, the following notational device is used: instead of writing the morphisms $\Psi _ { V , W }$ and $\Psi _ { W , V } ^ { - 1 }$ in the usual way as arrows, one writes them as braids and assumes that they point downwards:

Figure: b120420b
One writes another morphism $\phi : W \rightarrow Z$, say, as a node on a strand connecting $W$ to $Z$ and assumed to be pointing downwards. Functoriality says that morphisms can be pulled through braid crossings as

Figure: b120420c
Similarly for morphisms on the other strand. When the tensor product of several morphisms is applied, one writes their strands separately side by side, connecting the relevant objects in the tensor product. On the other hand, one is free to group some of the objects in the tensor product together as a single object and represent morphisms to and from it by a single strand. This notation is consistent precisely because of the hexagon conditions, which become

Figure: b120420d
The doubled strands on the left-hand side could be replaced by single strands for the composite morphisms.
The coherence theorem for braided categories then asserts that different routes between tensor product expressions by repeated applications of $\Phi$, $\Psi$ and their inverses compose to the same morphism if the corresponding braids are the same. In particular, for any object $V$ there is an action of the pure braid group $B _ { n }$ on 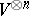 . The former can be presented as
. The former can be presented as
\begin{equation*} b _ { i } b _ { i + 1} b _ { i } = b _ { i + 1} b _ { i } b _ { i } + 1 , b _ { i } b _ { j } = b _ { j } b _ { i } , \quad | i - j | \geq 2, \end{equation*}
where $b _ { i }$ is represented by $\Psi$ acting in the $( i , i + 1 )$th copies of $V$. The representation usually has a kernel and $B _ { n }$ modulo this kernel is the Hecke algebra associated to an object in a braided category.
Finally, an object $V$ in a braided category is rigid if there are another object $V ^ { * }$ and morphisms $\operatorname{ev} _ { V } : V ^ { * } \otimes V \rightarrow \underline { 1 }$ and $\operatorname{coev}_V : \underline { 1 } \rightarrow V \otimes V ^ { * }$ such that
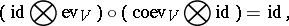 |
 |
(suppressing $\Phi$, $l$, $r$). Here, $V ^ { * }$ is called a left dual of $V$ and is unique up to isomorphism (there is a similar notion of right dual). $\mathcal{C}$ is called rigid if every object has such duals. Using diagrammatic notation one writes

Figure: b120420e
and the above axioms become

Figure: b120420f
Note that in a rigid braided category, morphisms 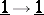 look like knots (cf. also Knot theory; Braid theory). Every knot presented on paper is in fact the closure of some braid, so with a little more structure (notably, both left and right duals) one can arrange that every oriented knot can be read from top to bottom as a morphism
look like knots (cf. also Knot theory; Braid theory). Every knot presented on paper is in fact the closure of some braid, so with a little more structure (notably, both left and right duals) one can arrange that every oriented knot can be read from top to bottom as a morphism 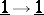 . Fixing an object $V$,
. Fixing an object $V$,
can be read as a left or right 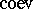 and
and
can be read as a left or right 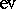 (in accordance with orientation). One can read braid crossings as $\Psi$ or $\Psi ^ { - 1 }$. The result is not quite a knot invariant but can usually be adjusted to become one.
(in accordance with orientation). One can read braid crossings as $\Psi$ or $\Psi ^ { - 1 }$. The result is not quite a knot invariant but can usually be adjusted to become one.
Examples.
Some standard examples of braided categories are provided by the following constructions over a ground field $k$. Its invertible elements are denoted $k ^ { * }$.
1) Fix $q \in k$, an $n$th root of unity. The category of anyspaces $\operatorname{Vec}_n$ consists of $\mathbf{Z} / n \mathbf{Z}$-graded vector spaces $V = \oplus _ { i = 0 } ^ { n - 1 } V _ { i }$ (where the elements of $V _ { i }$ have degree $i$). Morphisms are degree-preserving linear mappings. One takes the associator trivial and the braiding
\begin{equation*} \Psi _ { V , W } ( v \bigotimes w ) = q ^ { |v| | w | } w \bigotimes v \end{equation*}
for $v \in V$ and $w \in W$ of degree $v$, $w $, respectively.
Clearly, $\operatorname{Vec}_{1}$ is the usual category of vector spaces, while $\text{Vec}_2$ is the category of linear superspaces or ${\bf Z} / 2 {\bf Z}$-graded vector spaces. The category  of $\mathbf{Z}$-graded spaces is braided similarly for any $q \in k ^ { * }$.
of $\mathbf{Z}$-graded spaces is braided similarly for any $q \in k ^ { * }$.
A similar construction works for grading by any Abelian group $G$ equipped with a bicharacter $\beta : G \times G \rightarrow k ^ { * }$ (a function multiplicative in each argument) and braiding
\begin{equation*} \Psi _ { V , W } ( v \bigotimes w ) = \beta ( | v | , | w | ) w \bigotimes v \end{equation*}
on elements of degree $| v | , | w | \in G$.
2) If $G$ is a group and $\phi : G \times G \times G \rightarrow k ^ { * }$ a group $3$-cocycle, then the category of $G$-graded spaces is monoidal with associator
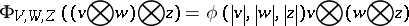 |
on elements of degree $| v | , | w | , | z | \in G$. If $G$ is Abelian and equipped with a quasi-bicharacter with respect to $\phi$, then the category is braided.
For example, the octonion algebra lives naturally in such a category with $G = \mathbf{Z} _ { 2 } \times \mathbf{Z} _ { 2 } \times \mathbf{Z} _ { 2 }$ and $\phi$ a certain coboundary.
3) The category of finite-dimensional representations of the quantum enveloping algebras (cf. also Quantum groups; Universal enveloping algebra) $U _ { q } ( \mathfrak { g } )$ associated to a semi-simple Lie algebra $\frak g$. Also, certain classes of infinite-dimensional representations. Associated to the standard representation of $U _ { q } ( \operatorname{sl} _ { 2 } )$ is the standard Hecke algebra defined by the additional relation $( b _ { i } - q ) ( b _ { i } + q ^ { - 1 } ) = 0$. The knot invariant associated to this same representation is the Jones knot polynomial.
In an algebraic formulation, if $H$, $\mathcal{R} \in H \otimes H$, is a quasi-triangular Hopf algebra, then its category $\square _ { H } \cal M$ of representations is braided with $\Psi = \tau \circ \mathcal{R}$, where one first acts with the quasi-triangular structure $\mathcal{R} \in H \otimes H$ and then applies the usual transposition mapping $\tau$.
4) The category of co-modules under the matrix quantum groups (cf. Quantum groups) $G_q$. For example, the quantum plane generated by $x , y$ modulo the relations $y x = q x y$ is covariant under $\operatorname{SL} _ { q } ( 2 )$ and hence lives as an algebra in its braided category of co-modules. Likewise, the category of co-modules under a quantum matrix bi-algebra $A ( R )$ associated to an invertible solution $R$ of the Yang–Baxter equation is braided.
In a general algebraic formulation, if $H$, $\mathcal{R} : H \otimes H \rightarrow k $, is a dual (or co-) quasi-triangular Hopf algebra, then its category of co-modules is braided by
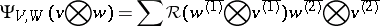 |
where $\sum _ { V } v ^ { \overline{( 1 ) }} \otimes v ^ { \overline{( 2 ) } }$ denotes the result of the co-action $V \rightarrow H \otimes V$.
5) If $H$ is any Hopf algebra with invertible antipode, then its category $\square _ { H } ^ { H } \mathcal{M}$ of crossed modules (also called Drinfel'd–Radford–Yetter modules) is braided. Here, objects are vector spaces $V$ which are both modules and co-modules under $H$, the two being compatible in the sense
\begin{equation*} \sum h_{ ( 1 )} v ^ { \overline{( 1 )} } \bigotimes h_{ ( 2 )} \rhd v ^ { \overline{( 2 )} } = \end{equation*}
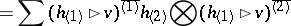 |
for $h \in H$ and $v \in V$, where $\triangleright$ denotes the action and $\sum h _ { ( 1 ) } \otimes h _ { ( 2 ) }$ denotes the co-product. The braiding is
\begin{equation*} \Psi _ { V , W } ( v \bigotimes w ) = \sum v ^ { \overline{( 1 )} } \rhd w \bigotimes v ^ { \overline{( 2 )} }. \end{equation*}
For example, if $\frak g$ is any Lie algebra and $U ( \mathfrak { g } )$ is its enveloping algebra (cf. also Universal enveloping algebra), then $V = k 1 \oplus \mathfrak g \subset U ( \mathfrak g )$ is a crossed module by the adjoint action and the co-product of $U ( \mathfrak { g } )$. The braiding induced on it is
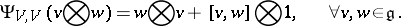 |
6) Let $\mathcal{C}$ be any monoidal category. Then its representation-theoretic dual category $\mathcal{C} ^ { \circ }$ (also called the double $D ( \mathcal{C} )$ or centre $Z (\cal C )$) is a braided category. Objects are pairs $( V , \lambda )$ where $V$ is an object of $\mathcal{C}$ and $\lambda _ { W } : V \otimes W \rightarrow W \otimes V$ is a collection of functorial isomorphisms representing the $\otimes$ of $\mathcal{C}$ in the sense
\begin{equation*} \lambda _ { \underline{1} } = \operatorname {id} , \lambda _ { W \bigotimes Z} = \lambda_{Z} \circ \lambda _ { W } \end{equation*}
($\Phi$, $l$, $r$ suppressed in this notation). The braiding is $\Psi _ { ( V , \lambda ) , ( W , \mu ) } = \lambda _ { W }$.
These constructions are in roughly increasing order of generality. Thus, the categorical dual or double construction applied to the category of $H$-modules yields the category of crossed modules $\square _ { H } ^ { H } \mathcal{M}$. These, in turn, are an elementary reformulation (and thereby a slight generalization to infinite-dimensional $H$) of the category of $D ( H )$-modules, where $D ( H )$ is the quantum double quasi-triangular Hopf algebra associated to any finite-dimensional Hopf algebra $H$. Meanwhile, a bicharacter on an Abelian group extends by linearity to a dual-quasi-triangular structure on the corresponding group algebra.
References
| [a1] | S. MacLane, "Categories for the working mathematician" , GTM , 5 , Springer (1974) |
| [a2] | A. Joyal, R. Street, "Braided monoidal categories" Math. Reports Macquarie Univ. , 86008 (1986) |
| [a3] | S. Majid, "Foundations of quantum group theory" , Cambridge Univ. Press (1995) |
Braided category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Braided_category&oldid=18411