Difference between revisions of "Booth lemniscate"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b0170001.png | ||
| + | $#A+1 = 14 n = 0 | ||
| + | $#C+1 = 14 : ~/encyclopedia/old_files/data/B017/B.0107000 Booth lemniscate | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A plane algebraic curve of order four whose equation in orthogonal Cartesian coordinates is | A plane algebraic curve of order four whose equation in orthogonal Cartesian coordinates is | ||
| − | + | $$ | |
| + | (x ^ {2} + y ^ {2} ) ^ {2} - | ||
| + | (2m ^ {2} + n) x ^ {2} - | ||
| + | (2m ^ {2} - n) y ^ {2} = 0. | ||
| + | $$ | ||
| − | If < | + | If $ | n | < 2 m ^ {2} $, |
| + | the Booth lemniscate is called elliptic (it has singular point $ O $( | ||
| + | Fig. a), where $ 0 < n < 2 m ^ {2} $). | ||
| + | If $ | n | > 2 m ^ {2} $, | ||
| + | the Booth lemniscate is called hyperbolic (it has a nodal point at the coordinate origin, cf. Fig. b, where $ n > 2 m ^ {2} $). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017000a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017000a.gif" /> | ||
| Line 15: | Line 35: | ||
The equation of an elliptic Booth lemniscate in polar coordinates is | The equation of an elliptic Booth lemniscate in polar coordinates is | ||
| − | + | $$ | |
| + | \rho ^ {2} = a ^ {2} \cos ^ {2} \phi + | ||
| + | b ^ {2} \sin ^ {2} \phi \ \ | ||
| + | \textrm{ or } \ \rho \equiv 0. | ||
| + | $$ | ||
| − | If | + | If $ n > 2 m ^ {2} $, |
| + | the equation of a hyperbolic Booth lemniscate has the form | ||
| − | + | $$ | |
| + | \rho ^ {2} = \ | ||
| + | a ^ {2} \cos ^ {2} \phi - b ^ {2} \sin ^ {2} \phi ; | ||
| + | $$ | ||
| − | and if < | + | and if $ n < -2 m ^ {2} $ |
| − | + | $$ | |
| + | \rho ^ {2} = \ | ||
| + | - a ^ {2} \cos ^ {2} \phi + b ^ {2} \sin ^ {2} \phi | ||
| + | $$ | ||
| − | + | $$ | |
| + | (a ^ {2} = | 2m ^ {2} + n | ,\ b ^ {2} = | 2m ^ {2} - n | ). | ||
| + | $$ | ||
The arc length of a Booth lemniscate is expressed by elliptic integrals. The area bounded by an elliptic Booth lemniscate is | The arc length of a Booth lemniscate is expressed by elliptic integrals. The area bounded by an elliptic Booth lemniscate is | ||
| − | + | $$ | |
| + | S = { | ||
| + | \frac \pi {2} | ||
| + | } | ||
| + | (a ^ {2} + b ^ {2} ), | ||
| + | $$ | ||
while that bounded by a hyperbolic Booth lemniscate is | while that bounded by a hyperbolic Booth lemniscate is | ||
| − | + | $$ | |
| + | S = | ||
| + | \frac{a ^ {2} - b ^ {2} }{2} | ||
| + | \ | ||
| + | \mathop{\rm arctg} { | ||
| + | \frac{a}{b} | ||
| + | } + { | ||
| + | \frac{ab}{2} | ||
| + | } . | ||
| + | $$ | ||
The Booth lemniscate is a special case of a [[Persian curve|Persian curve]]. | The Booth lemniscate is a special case of a [[Persian curve|Persian curve]]. | ||
Revision as of 06:28, 30 May 2020
A plane algebraic curve of order four whose equation in orthogonal Cartesian coordinates is
$$ (x ^ {2} + y ^ {2} ) ^ {2} - (2m ^ {2} + n) x ^ {2} - (2m ^ {2} - n) y ^ {2} = 0. $$
If $ | n | < 2 m ^ {2} $, the Booth lemniscate is called elliptic (it has singular point $ O $( Fig. a), where $ 0 < n < 2 m ^ {2} $). If $ | n | > 2 m ^ {2} $, the Booth lemniscate is called hyperbolic (it has a nodal point at the coordinate origin, cf. Fig. b, where $ n > 2 m ^ {2} $).
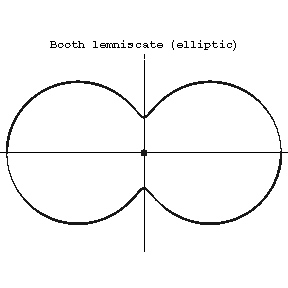
Figure: b017000a
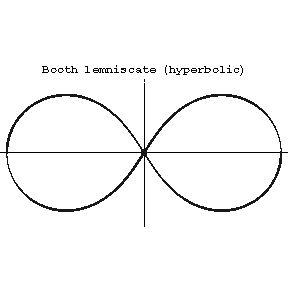
Figure: b017000b
The equation of an elliptic Booth lemniscate in polar coordinates is
$$ \rho ^ {2} = a ^ {2} \cos ^ {2} \phi + b ^ {2} \sin ^ {2} \phi \ \ \textrm{ or } \ \rho \equiv 0. $$
If $ n > 2 m ^ {2} $, the equation of a hyperbolic Booth lemniscate has the form
$$ \rho ^ {2} = \ a ^ {2} \cos ^ {2} \phi - b ^ {2} \sin ^ {2} \phi ; $$
and if $ n < -2 m ^ {2} $
$$ \rho ^ {2} = \ - a ^ {2} \cos ^ {2} \phi + b ^ {2} \sin ^ {2} \phi $$
$$ (a ^ {2} = | 2m ^ {2} + n | ,\ b ^ {2} = | 2m ^ {2} - n | ). $$
The arc length of a Booth lemniscate is expressed by elliptic integrals. The area bounded by an elliptic Booth lemniscate is
$$ S = { \frac \pi {2} } (a ^ {2} + b ^ {2} ), $$
while that bounded by a hyperbolic Booth lemniscate is
$$ S = \frac{a ^ {2} - b ^ {2} }{2} \ \mathop{\rm arctg} { \frac{a}{b} } + { \frac{ab}{2} } . $$
The Booth lemniscate is a special case of a Persian curve.
Named after J. Booth [1].
References
| [1] | J. Booth, "A treatise on some new geometrical methods" , 1–2 , London pp. 1873–1877 |
| [2] | A.A. Savelov, "Planar curves" , Moscow (1960) pp. 144–146 (In Russian) |
Booth lemniscate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Booth_lemniscate&oldid=18130