Difference between revisions of "Omega-squared distribution"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | o0681702.png | ||
| + | $#A+1 = 12 n = 1 | ||
| + | $#C+1 = 12 : ~/encyclopedia/old_files/data/O068/O.0608170 \BQT Omega\AAhsquared\EQT distribution, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | '' $ \omega ^ {2} $- | ||
| + | distribution'' | ||
The [[Probability distribution|probability distribution]] of the random variable | The [[Probability distribution|probability distribution]] of the random variable | ||
| − | + | $$ | |
| + | \omega ^ {2} = \int\limits _ { 0 } ^ { 1 } Z ^ {2} ( t) dt, | ||
| + | $$ | ||
| − | where | + | where $ Z( t) $ |
| + | is a conditional [[Wiener process|Wiener process]] (conditioned on $ Z ( 1) = 0 $). | ||
| + | The characteristic function of the "omega-squared" distribution is expressed by the formula | ||
| − | + | $$ | |
| + | {\mathsf E} e ^ {it \omega ^ {2} } = \prod _ { k= } 1 ^ \infty | ||
| + | \left ( 1 - | ||
| + | \frac{2it }{\pi ^ {2} k ^ {2} } | ||
| + | \right ) ^ {-} 1/2 . | ||
| + | $$ | ||
| − | In mathematical statistics, the "omega-squared" distribution is often found in the following circumstances. Let | + | In mathematical statistics, the "omega-squared" distribution is often found in the following circumstances. Let $ X _ {1} \dots X _ {n} $ |
| + | be independent random variables, uniformly distributed on $ [ 0, 1] $, | ||
| + | according to which an empirical distribution function $ F _ {n} ( \cdot ) $ | ||
| + | is constructed. In this case, the process | ||
| − | + | $$ | |
| + | Z _ {n} ( t) = \sqrt n ( F _ {n} ( t) - t) | ||
| + | $$ | ||
converges weakly to a conditional Wiener process, from which it follows that | converges weakly to a conditional Wiener process, from which it follows that | ||
| − | < | + | $$ |
| + | \lim\limits _ {n \rightarrow \infty } {\mathsf P} \left \{ \int\limits _ { 0 } ^ { 1 } Z _ {n} ^ {2} ( t) dt < \lambda \right \} = \ | ||
| + | {\mathsf P} \{ \omega ^ {2} < \lambda \} = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | 1 - | ||
| + | \frac{2} \pi | ||
| + | \sum _ { k= } 1 ^ \infty (- 1) ^ {k-} 1 \int\limits _ {( 2k- 1) \pi } ^ { {2k } \pi } | ||
| + | \frac{e ^ {- t ^ {2} \lambda / 2 } | ||
| + | }{\sqrt {- t \sin t } } | ||
| + | dt,\ \lambda > 0 . | ||
| + | $$ | ||
See also [[Cramér–von Mises test|Cramér–von Mises test]]. | See also [[Cramér–von Mises test|Cramér–von Mises test]]. | ||
| Line 23: | Line 61: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.V. Smirnov, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068170/o06817013.png" />-distribution" ''Mat. Sb.'' , '''2''' (1937) pp. 973–993 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness of fit" criteria based on stochastic processes" ''Ann. Math. Stat.'' , '''23''' (1952) pp. 193–212</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.V. Smirnov, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068170/o06817013.png" />-distribution" ''Mat. Sb.'' , '''2''' (1937) pp. 973–993 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness of fit" criteria based on stochastic processes" ''Ann. Math. Stat.'' , '''23''' (1952) pp. 193–212</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The "conditional Wiener process" | + | The "conditional Wiener process" $ Z $ |
| + | is usually referred to in the Western literature as tied-down Brownian motion, pinned Brownian motion or as the Brownian bridge. | ||
The pioneering paper is [[#References|[a1]]]. | The pioneering paper is [[#References|[a1]]]. | ||
Revision as of 08:03, 6 June 2020
$ \omega ^ {2} $-
distribution
The probability distribution of the random variable
$$ \omega ^ {2} = \int\limits _ { 0 } ^ { 1 } Z ^ {2} ( t) dt, $$
where $ Z( t) $ is a conditional Wiener process (conditioned on $ Z ( 1) = 0 $). The characteristic function of the "omega-squared" distribution is expressed by the formula
$$ {\mathsf E} e ^ {it \omega ^ {2} } = \prod _ { k= } 1 ^ \infty \left ( 1 - \frac{2it }{\pi ^ {2} k ^ {2} } \right ) ^ {-} 1/2 . $$
In mathematical statistics, the "omega-squared" distribution is often found in the following circumstances. Let $ X _ {1} \dots X _ {n} $ be independent random variables, uniformly distributed on $ [ 0, 1] $, according to which an empirical distribution function $ F _ {n} ( \cdot ) $ is constructed. In this case, the process
$$ Z _ {n} ( t) = \sqrt n ( F _ {n} ( t) - t) $$
converges weakly to a conditional Wiener process, from which it follows that
$$ \lim\limits _ {n \rightarrow \infty } {\mathsf P} \left \{ \int\limits _ { 0 } ^ { 1 } Z _ {n} ^ {2} ( t) dt < \lambda \right \} = \ {\mathsf P} \{ \omega ^ {2} < \lambda \} = $$
$$ = \ 1 - \frac{2} \pi \sum _ { k= } 1 ^ \infty (- 1) ^ {k-} 1 \int\limits _ {( 2k- 1) \pi } ^ { {2k } \pi } \frac{e ^ {- t ^ {2} \lambda / 2 } }{\sqrt {- t \sin t } } dt,\ \lambda > 0 . $$
See also Cramér–von Mises test.
References
| [1] | N.V. Smirnov, "On the 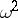 -distribution" Mat. Sb. , 2 (1937) pp. 973–993 (In Russian) -distribution" Mat. Sb. , 2 (1937) pp. 973–993 (In Russian) |
| [2] | T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness of fit" criteria based on stochastic processes" Ann. Math. Stat. , 23 (1952) pp. 193–212 |
Comments
The "conditional Wiener process" $ Z $ is usually referred to in the Western literature as tied-down Brownian motion, pinned Brownian motion or as the Brownian bridge.
The pioneering paper is [a1].
References
| [a1] | D.A. Darling, "The Cramér–Smirnov test in the parametric case" Ann. Math. Stat. , 26 (1955) pp. 1–20 |
| [a2] | J. Durbin, "Distribution theory for tests based on the sample distribution function" , SIAM (1973) |
Omega-squared distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Omega-squared_distribution&oldid=17313