Difference between revisions of "Ovoid(2)"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | o0706701.png | ||
| + | $#A+1 = 38 n = 1 | ||
| + | $#C+1 = 38 : ~/encyclopedia/old_files/data/O070/O.0700670 Ovoid, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''ovaloid'' | ''ovaloid'' | ||
| − | A set | + | A set $ O $ |
| + | of points in some space which is intersected by an arbitrary straight line in at most two points, and such that the tangents to $ O $ | ||
| + | at each of its points cover exactly a hyperplane. In projective space a non-ruled [[Quadric|quadric]] is an ovoid. This term is mainly used in finite geometries. | ||
| − | In finite projective spaces of dimension greater than three, ovoids do not exist. In three-dimensional spaces of order | + | In finite projective spaces of dimension greater than three, ovoids do not exist. In three-dimensional spaces of order $ q > 2 $, |
| + | an ovoid is a maximal $ k $- | ||
| + | cap (cf. [[Cap|Cap]]) and consists of $ q ^ {2} + 1 $ | ||
| + | points, and for odd $ q $ | ||
| + | any ovoid is an elliptic quadric (see [[#References|[1]]]). In a plane of order $ q $, | ||
| + | an ovoid is called an oval, and consists of $ q + 1 $ | ||
| + | points. In a Desarguesian plane of odd order, any oval is uniquely representable as a non-degenerate conic over a Galois field (see [[#References|[2]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Segre, "Introduction to Galois geometries" ''Atti Accad. Naz. Lincei'' , '''8''' (1967) pp. 133–236</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Segre, "Ovals in a finite projective plane" ''Canad. J. Math.'' , '''7''' (1955) pp. 414–416</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Tits, "Ovoids à translations" ''Rend. Mat. e Appl.'' , '''21''' (1962) pp. 37–59</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B. Segre, "Introduction to Galois geometries" ''Atti Accad. Naz. Lincei'' , '''8''' (1967) pp. 133–236</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Segre, "Ovals in a finite projective plane" ''Canad. J. Math.'' , '''7''' (1955) pp. 414–416</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Tits, "Ovoids à translations" ''Rend. Mat. e Appl.'' , '''21''' (1962) pp. 37–59</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
For Desarguesian planes of even order there are counterexamples to the last statement above. | For Desarguesian planes of even order there are counterexamples to the last statement above. | ||
| − | An ovoid in | + | An ovoid in $ \mathbf P ^ {3} $ |
| + | is a set $ {\mathcal O} $ | ||
| + | of points such that no four lie in a plane and such that at each $ A \in {\mathcal O} $ | ||
| + | there is a unique hyperplane through $ A $ | ||
| + | tangent to $ {\mathcal O} $ | ||
| + | at that point. Here "tangent" means that the intersection of $ {\mathcal O} $ | ||
| + | with the hyperplane consists only of $ A $ | ||
| + | itself. | ||
| − | For a finite field of odd characteristic the ovoids in | + | For a finite field of odd characteristic the ovoids in $ \mathbf P ^ {3} $ |
| + | are precisely the zeros of a quadratic form of Witt index 1, [[#References|[a1]]]. | ||
| − | An ovoid in a [[Polar space|polar space]] (in particular, in a generalized [[Quadrangle|quadrangle]]) is a collection | + | An ovoid in a [[Polar space|polar space]] (in particular, in a generalized [[Quadrangle|quadrangle]]) is a collection $ {\mathcal O} $ |
| + | of points such that every maximal singular subspace intersects $ {\mathcal O} $ | ||
| + | in exactly one point. A spread in a generalized quadrangle is a set $ {\mathcal R} $ | ||
| + | of lines such that each point is incident with one line of $ {\mathcal R} $. | ||
| + | A spread is an ovoid in the dual generalized quadrangle. An ovoid in a finite generalized quadrangle of order $ ( s, t) $ | ||
| + | has cardinality $ st+ 1 $. | ||
A (trivial) example of an ovoid is the set of encircled points in the grid (cf. [[Quadrangle|Quadrangle]]) depicted below: | A (trivial) example of an ovoid is the set of encircled points in the grid (cf. [[Quadrangle|Quadrangle]]) depicted below: | ||
| Line 25: | Line 56: | ||
Figure: o070670a | Figure: o070670a | ||
| − | The connection between the abstract notion of an ovoid in a polar space and an ovoid in | + | The connection between the abstract notion of an ovoid in a polar space and an ovoid in $ \mathbf P ^ {3} $ |
| + | is as follows. Consider the classical generalized quadrangle defined by a symplectic bilinear form $ Q $. | ||
| + | I.e. the points are the points of $ \mathbf P ^ {3} $( | ||
| + | which are all isotropic) and the lines are the totally isotropic lines of $ \mathbf P ^ {3} $ | ||
| + | with respect to this form. Then an ovoid in this generalized quadrangle viewed as a subset of $ \mathbf P ^ {3} $ | ||
| + | is an ovoid in the sense of the geometric version of the concept. (The tangent plane to $ ( y _ {0} : y _ {1} : y _ {2} : y _ {3} ) = A \in {\mathcal O} $ | ||
| + | is $ A ^ \perp = \{ {x \in \mathbf P ^ {3} } : {Q( x, y) = 0 } \} $. | ||
| − | Let | + | Let $ \Omega ^ {+} ( 2n, \mathbf F ) $, |
| + | $ \mathbf F $ | ||
| + | a finite field, be the (classical) polar space defined by the bilinear form | ||
| − | + | $$ | |
| + | x _ {0} x _ {1} + x _ {2} x _ {3} + \dots + x _ {2n-} 2 x _ {2n-} 1 . | ||
| + | $$ | ||
| − | Ovoids in | + | Ovoids in $ \Omega ^ {+} ( 6, \mathbf F ) $ |
| + | are used to obtain non-Desarguesian translation planes. From one "master" ovoid in $ \Omega ^ {+} ( 8, \mathbf F ) $ | ||
| + | one obtains many ovoids in $ \Omega ^ {+} ( 6, \mathbf F ) $. | ||
| + | It is an open problem whether there are ovoids in $ \Omega ^ {+} ( 10, \mathbf F ) $. | ||
| + | There are none $ \Omega ^ {+} ( 10, \mathbf F _ {3} ) $, | ||
| + | [[#References|[a4]]], or in $ \Omega ^ {+} ( 10 , \mathbf F _ {2} ) $, | ||
| + | [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Barlotti, "Un' estenzione del teorema di Segre–Kustaanheimo" ''Boll. Un. Mat. Ital. (3)'' , '''10''' (1955) pp. 498–506</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S.E. Pagne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G. Mason, E.E. Shult, "The Klein correspondence and the ubiquity of certain translation planes" ''Geom. Dedicata'' , '''21''' (1986) pp. 29–50</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E.E. Shult, "Nonexistence of ovoids in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070670/o07067039.png" />" ''J. Comb. Theory, Ser. A'' , '''51''' (1989) pp. 250–257</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W.M. Kantor, "Ovoids and translation planes" ''Canad. J. Math.'' , '''34''' (1982) pp. 1195–1207</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Clarendon Press (1985) pp. Chapt. 16</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Barlotti, "Un' estenzione del teorema di Segre–Kustaanheimo" ''Boll. Un. Mat. Ital. (3)'' , '''10''' (1955) pp. 498–506</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S.E. Pagne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G. Mason, E.E. Shult, "The Klein correspondence and the ubiquity of certain translation planes" ''Geom. Dedicata'' , '''21''' (1986) pp. 29–50</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E.E. Shult, "Nonexistence of ovoids in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070670/o07067039.png" />" ''J. Comb. Theory, Ser. A'' , '''51''' (1989) pp. 250–257</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W.M. Kantor, "Ovoids and translation planes" ''Canad. J. Math.'' , '''34''' (1982) pp. 1195–1207</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Clarendon Press (1985) pp. Chapt. 16</TD></TR></table> | ||
Revision as of 08:04, 6 June 2020
ovaloid
A set $ O $ of points in some space which is intersected by an arbitrary straight line in at most two points, and such that the tangents to $ O $ at each of its points cover exactly a hyperplane. In projective space a non-ruled quadric is an ovoid. This term is mainly used in finite geometries.
In finite projective spaces of dimension greater than three, ovoids do not exist. In three-dimensional spaces of order $ q > 2 $, an ovoid is a maximal $ k $- cap (cf. Cap) and consists of $ q ^ {2} + 1 $ points, and for odd $ q $ any ovoid is an elliptic quadric (see [1]). In a plane of order $ q $, an ovoid is called an oval, and consists of $ q + 1 $ points. In a Desarguesian plane of odd order, any oval is uniquely representable as a non-degenerate conic over a Galois field (see [2]).
References
| [1] | B. Segre, "Introduction to Galois geometries" Atti Accad. Naz. Lincei , 8 (1967) pp. 133–236 |
| [2] | B. Segre, "Ovals in a finite projective plane" Canad. J. Math. , 7 (1955) pp. 414–416 |
| [3] | J. Tits, "Ovoids à translations" Rend. Mat. e Appl. , 21 (1962) pp. 37–59 |
Comments
For Desarguesian planes of even order there are counterexamples to the last statement above.
An ovoid in $ \mathbf P ^ {3} $ is a set $ {\mathcal O} $ of points such that no four lie in a plane and such that at each $ A \in {\mathcal O} $ there is a unique hyperplane through $ A $ tangent to $ {\mathcal O} $ at that point. Here "tangent" means that the intersection of $ {\mathcal O} $ with the hyperplane consists only of $ A $ itself.
For a finite field of odd characteristic the ovoids in $ \mathbf P ^ {3} $ are precisely the zeros of a quadratic form of Witt index 1, [a1].
An ovoid in a polar space (in particular, in a generalized quadrangle) is a collection $ {\mathcal O} $ of points such that every maximal singular subspace intersects $ {\mathcal O} $ in exactly one point. A spread in a generalized quadrangle is a set $ {\mathcal R} $ of lines such that each point is incident with one line of $ {\mathcal R} $. A spread is an ovoid in the dual generalized quadrangle. An ovoid in a finite generalized quadrangle of order $ ( s, t) $ has cardinality $ st+ 1 $.
A (trivial) example of an ovoid is the set of encircled points in the grid (cf. Quadrangle) depicted below:

Figure: o070670a
The connection between the abstract notion of an ovoid in a polar space and an ovoid in $ \mathbf P ^ {3} $ is as follows. Consider the classical generalized quadrangle defined by a symplectic bilinear form $ Q $. I.e. the points are the points of $ \mathbf P ^ {3} $( which are all isotropic) and the lines are the totally isotropic lines of $ \mathbf P ^ {3} $ with respect to this form. Then an ovoid in this generalized quadrangle viewed as a subset of $ \mathbf P ^ {3} $ is an ovoid in the sense of the geometric version of the concept. (The tangent plane to $ ( y _ {0} : y _ {1} : y _ {2} : y _ {3} ) = A \in {\mathcal O} $ is $ A ^ \perp = \{ {x \in \mathbf P ^ {3} } : {Q( x, y) = 0 } \} $.
Let $ \Omega ^ {+} ( 2n, \mathbf F ) $, $ \mathbf F $ a finite field, be the (classical) polar space defined by the bilinear form
$$ x _ {0} x _ {1} + x _ {2} x _ {3} + \dots + x _ {2n-} 2 x _ {2n-} 1 . $$
Ovoids in $ \Omega ^ {+} ( 6, \mathbf F ) $ are used to obtain non-Desarguesian translation planes. From one "master" ovoid in $ \Omega ^ {+} ( 8, \mathbf F ) $ one obtains many ovoids in $ \Omega ^ {+} ( 6, \mathbf F ) $. It is an open problem whether there are ovoids in $ \Omega ^ {+} ( 10, \mathbf F ) $. There are none $ \Omega ^ {+} ( 10, \mathbf F _ {3} ) $, [a4], or in $ \Omega ^ {+} ( 10 , \mathbf F _ {2} ) $, [a5].
References
| [a1] | A. Barlotti, "Un' estenzione del teorema di Segre–Kustaanheimo" Boll. Un. Mat. Ital. (3) , 10 (1955) pp. 498–506 |
| [a2] | S.E. Pagne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984) |
| [a3] | G. Mason, E.E. Shult, "The Klein correspondence and the ubiquity of certain translation planes" Geom. Dedicata , 21 (1986) pp. 29–50 |
| [a4] | E.E. Shult, "Nonexistence of ovoids in 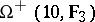 " J. Comb. Theory, Ser. A , 51 (1989) pp. 250–257 " J. Comb. Theory, Ser. A , 51 (1989) pp. 250–257 |
| [a5] | W.M. Kantor, "Ovoids and translation planes" Canad. J. Math. , 34 (1982) pp. 1195–1207 |
| [a6] | J.W.P. Hirschfeld, "Finite projective spaces of three dimensions" , Clarendon Press (1985) pp. Chapt. 16 |
Ovoid(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ovoid(2)&oldid=17115