Difference between revisions of "L-adic-cohomology"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | l0570202.png | ||
| + | $#A+1 = 80 n = 3 | ||
| + | $#C+1 = 80 : ~/encyclopedia/old_files/data/L057/L.0507020 \BMI l\EMI\AAhadic cohomology | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
One of the constructions of cohomology of abstract algebraic varieties and schemes. Etale cohomologies (cf. [[Etale cohomology|Etale cohomology]]) of schemes are torsion modules. Cohomology with coefficients in rings of characteristic zero is used for various purposes, mainly in the proof of the [[Lefschetz formula|Lefschetz formula]] and its application to zeta-functions. It is obtained from étale cohomology by passing to the projective limit. | One of the constructions of cohomology of abstract algebraic varieties and schemes. Etale cohomologies (cf. [[Etale cohomology|Etale cohomology]]) of schemes are torsion modules. Cohomology with coefficients in rings of characteristic zero is used for various purposes, mainly in the proof of the [[Lefschetz formula|Lefschetz formula]] and its application to zeta-functions. It is obtained from étale cohomology by passing to the projective limit. | ||
| − | Let | + | Let $ l $ |
| + | be a prime number; an $ l $- | ||
| + | adic sheaf on a scheme $ X $ | ||
| + | is a projective system $ {( F _ {n} ) } _ {n \in \mathbf N } $ | ||
| + | of étale Abelian sheaves $ F _ {n} $ | ||
| + | such that, for all $ n $, | ||
| + | the transfer homomorphisms $ F _ {n+} 1 \rightarrow F _ {n} $ | ||
| + | are equivalent to the canonical morphism $ F _ {n+} 1 \rightarrow F _ {n+} 1 / l ^ {n} F _ {n+} 1 $. | ||
| + | An $ l $- | ||
| + | adic sheaf $ F $ | ||
| + | is said to be constructible (respectively, locally constant) if all sheaves $ F _ {n} $ | ||
| + | are constructible (locally constant) étale sheaves. There exists a natural equivalence of the category of locally constant constructible sheaves on a connected scheme $ X $ | ||
| + | and the category of modules of finite type over the ring $ \mathbf Z _ {l} $ | ||
| + | of integral $ l $- | ||
| + | adic numbers which are continuously acted upon from the left by the fundamental group of the scheme $ X $. | ||
| + | This proves that locally constant constructible sheaves are abstract analogues of systems of local coefficients in topology. Examples of constructible $ l $- | ||
| + | adic sheaves include the sheaf $ \mathbf Z _ {l,X} = {( ( \mathbf Z / l ^ {n} \mathbf Z ) _ {X} ) } _ {n \in \mathbf N } $, | ||
| + | and the Tate sheaves $ \mathbf Z _ {l} ( m) _ {X} = ( \mu _ {l ^ {n} , X } ^ {\otimes ^ {m} } ) _ {n \in \mathbf N } $( | ||
| + | where $ ( \mathbf Z / l ^ {n} \mathbf Z ) _ {X} $ | ||
| + | is the constant sheaf on $ X $ | ||
| + | associated with the group $ \mathbf Z / l ^ {n} \mathbf Z $, | ||
| + | while $ \mu _ {l ^ {n} , X } $ | ||
| + | is the sheaf of $ l ^ {n} $- | ||
| + | th power roots of unity on $ X $). | ||
| + | If $ A $ | ||
| + | is an [[Abelian scheme|Abelian scheme]] over $ X $, | ||
| + | then $ T _ {l} ( A) = {( A _ {l ^ {n} } ) } _ {n \in \mathbf N } $( | ||
| + | where $ A _ {l ^ {n} } $ | ||
| + | is the kernel of multiplication by $ l ^ {n} $ | ||
| + | in $ A $) | ||
| + | forms a locally constant constructible $ l $- | ||
| + | adic sheaf on $ X $, | ||
| + | called the Tate module of $ A $. | ||
| − | Let | + | Let $ X $ |
| + | be a scheme over a field $ k $, | ||
| + | let $ \overline{X}\; = X \otimes _ {k} \overline{k}\; _ {s} $ | ||
| + | be the scheme obtained from $ X $ | ||
| + | by changing the base from $ k $ | ||
| + | to the separable closure $ \overline{k}\; _ {s} $ | ||
| + | of the field $ k $, | ||
| + | and let $ F = ( F _ {n} ) $ | ||
| + | be an $ l $- | ||
| + | adic sheaf on $ X $; | ||
| + | the étale cohomology $ H ^ {i} ( \overline{X}\; , \overline{F}\; _ {n} ) $ | ||
| + | then defines a projective system $ ( H ^ {i} ( \overline{X}\; , \overline{F}\; _ {n} )) _ {n \in \mathbf N } $ | ||
| + | of $ \mathop{\rm Gal} ( \overline{k}\; _ {s} / k ) $- | ||
| + | modules. The projective limit $ H ^ {i} ( \overline{X}\; , F ) = \lim\limits _ {\leftarrow n } H ^ {i} ( \overline{X}\; , \overline{F}\; _ {n} ) $ | ||
| + | is naturally equipped with the structure of a $ \mathbf Z _ {l} $- | ||
| + | module on which $ \mathop{\rm Gal} ( \overline{k}\; _ {s} / k ) $ | ||
| + | acts continuously with respect to the $ l $- | ||
| + | adic topology. It is called the $ i $- | ||
| + | th $ l $- | ||
| + | adic cohomology of the sheaf $ F $ | ||
| + | on $ X $. | ||
| + | If $ k = \overline{k}\; _ {s} $, | ||
| + | the usual notation is $ H ^ {i} ( \overline{X}\; , F ) = H ^ {i} ( X, F ) $. | ||
| + | The fundamental theorems in étale cohomology apply to $ l $- | ||
| + | adic cohomology of constructible $ l $- | ||
| + | adic sheaves. If $ \mathbf Q _ {l} $ | ||
| + | is the field of rational $ l $- | ||
| + | adic numbers, then the $ \mathbf Q _ {l} $- | ||
| + | spaces $ H _ {l} ^ {i} ( \overline{X}\; ) = H ^ {i} ( \overline{X}\; , \mathbf Z _ {l} ) \otimes \mathbf Q _ {l} $ | ||
| + | are called the rational $ l $- | ||
| + | adic cohomology of the scheme $ X $. | ||
| + | Their dimensions $ b _ {i} ( X; l) $( | ||
| + | if defined) are called the $ i $- | ||
| + | th Betti numbers of $ X $. | ||
| + | For complete $ k $- | ||
| + | schemes the numbers $ b _ {i} ( X; l) $ | ||
| + | are defined and are independent of $ l $( | ||
| + | $ l \neq \mathop{\rm char} k $). | ||
| + | If $ k $ | ||
| + | is an algebraically closed field of characteristic $ p $ | ||
| + | and if $ l \neq p $, | ||
| + | then the assignment of the spaces $ H _ {l} ^ {i} ( X) $ | ||
| + | to a smooth complete $ k $- | ||
| + | variety defines a [[Weil cohomology|Weil cohomology]]. If $ k = \mathbf C $ | ||
| + | is the field of complex numbers, the comparison theorem $ H _ {l} ^ {i} = H ^ {i} ( X, \mathbf Q ) \otimes \mathbf Q _ {l} $ | ||
| + | is valid. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, "Formule de Lefschetz et rationalité des fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702086.png" />" , ''Sem. Bourbaki'' , '''17''' : 279 (1964–1965)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Grothendieck, "Formule de Lefschetz et rationalité des fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702086.png" />" , ''Sem. Bourbaki'' , '''17''' : 279 (1964–1965)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The fact (mentioned above) that for complete | + | The fact (mentioned above) that for complete $ k $- |
| + | schemes the Betti numbers are independent of $ l $ | ||
| + | follows from Deligne's proof of the Weil conjectures (cf. also [[Zeta-function|Zeta-function]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Grothendieck, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702089.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702090.png" />" , ''SGA 5'' , ''Lect. notes in math.'' , '''589''' , Springer (1977)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Freitag, R. Kiehl, "Etale cohomology and the Weil conjectures" , Springer (1988)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–307</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil II" ''Publ. Math. IHES'' , '''52''' (1980) pp. 137–252</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Grothendieck, "Cohomologie <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702089.png" />-adique et fonctions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l057/l057020/l05702090.png" />" , ''SGA 5'' , ''Lect. notes in math.'' , '''589''' , Springer (1977)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Freitag, R. Kiehl, "Etale cohomology and the Weil conjectures" , Springer (1988)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil I" ''Publ. Math. IHES'' , '''43''' (1974) pp. 273–307</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P. Deligne, "La conjecture de Weil II" ''Publ. Math. IHES'' , '''52''' (1980) pp. 137–252</TD></TR></table> | ||
Revision as of 22:15, 5 June 2020
One of the constructions of cohomology of abstract algebraic varieties and schemes. Etale cohomologies (cf. Etale cohomology) of schemes are torsion modules. Cohomology with coefficients in rings of characteristic zero is used for various purposes, mainly in the proof of the Lefschetz formula and its application to zeta-functions. It is obtained from étale cohomology by passing to the projective limit.
Let $ l $ be a prime number; an $ l $- adic sheaf on a scheme $ X $ is a projective system $ {( F _ {n} ) } _ {n \in \mathbf N } $ of étale Abelian sheaves $ F _ {n} $ such that, for all $ n $, the transfer homomorphisms $ F _ {n+} 1 \rightarrow F _ {n} $ are equivalent to the canonical morphism $ F _ {n+} 1 \rightarrow F _ {n+} 1 / l ^ {n} F _ {n+} 1 $. An $ l $- adic sheaf $ F $ is said to be constructible (respectively, locally constant) if all sheaves $ F _ {n} $ are constructible (locally constant) étale sheaves. There exists a natural equivalence of the category of locally constant constructible sheaves on a connected scheme $ X $ and the category of modules of finite type over the ring $ \mathbf Z _ {l} $ of integral $ l $- adic numbers which are continuously acted upon from the left by the fundamental group of the scheme $ X $. This proves that locally constant constructible sheaves are abstract analogues of systems of local coefficients in topology. Examples of constructible $ l $- adic sheaves include the sheaf $ \mathbf Z _ {l,X} = {( ( \mathbf Z / l ^ {n} \mathbf Z ) _ {X} ) } _ {n \in \mathbf N } $, and the Tate sheaves $ \mathbf Z _ {l} ( m) _ {X} = ( \mu _ {l ^ {n} , X } ^ {\otimes ^ {m} } ) _ {n \in \mathbf N } $( where $ ( \mathbf Z / l ^ {n} \mathbf Z ) _ {X} $ is the constant sheaf on $ X $ associated with the group $ \mathbf Z / l ^ {n} \mathbf Z $, while $ \mu _ {l ^ {n} , X } $ is the sheaf of $ l ^ {n} $- th power roots of unity on $ X $). If $ A $ is an Abelian scheme over $ X $, then $ T _ {l} ( A) = {( A _ {l ^ {n} } ) } _ {n \in \mathbf N } $( where $ A _ {l ^ {n} } $ is the kernel of multiplication by $ l ^ {n} $ in $ A $) forms a locally constant constructible $ l $- adic sheaf on $ X $, called the Tate module of $ A $.
Let $ X $ be a scheme over a field $ k $, let $ \overline{X}\; = X \otimes _ {k} \overline{k}\; _ {s} $ be the scheme obtained from $ X $ by changing the base from $ k $ to the separable closure $ \overline{k}\; _ {s} $ of the field $ k $, and let $ F = ( F _ {n} ) $ be an $ l $- adic sheaf on $ X $; the étale cohomology $ H ^ {i} ( \overline{X}\; , \overline{F}\; _ {n} ) $ then defines a projective system $ ( H ^ {i} ( \overline{X}\; , \overline{F}\; _ {n} )) _ {n \in \mathbf N } $ of $ \mathop{\rm Gal} ( \overline{k}\; _ {s} / k ) $- modules. The projective limit $ H ^ {i} ( \overline{X}\; , F ) = \lim\limits _ {\leftarrow n } H ^ {i} ( \overline{X}\; , \overline{F}\; _ {n} ) $ is naturally equipped with the structure of a $ \mathbf Z _ {l} $- module on which $ \mathop{\rm Gal} ( \overline{k}\; _ {s} / k ) $ acts continuously with respect to the $ l $- adic topology. It is called the $ i $- th $ l $- adic cohomology of the sheaf $ F $ on $ X $. If $ k = \overline{k}\; _ {s} $, the usual notation is $ H ^ {i} ( \overline{X}\; , F ) = H ^ {i} ( X, F ) $. The fundamental theorems in étale cohomology apply to $ l $- adic cohomology of constructible $ l $- adic sheaves. If $ \mathbf Q _ {l} $ is the field of rational $ l $- adic numbers, then the $ \mathbf Q _ {l} $- spaces $ H _ {l} ^ {i} ( \overline{X}\; ) = H ^ {i} ( \overline{X}\; , \mathbf Z _ {l} ) \otimes \mathbf Q _ {l} $ are called the rational $ l $- adic cohomology of the scheme $ X $. Their dimensions $ b _ {i} ( X; l) $( if defined) are called the $ i $- th Betti numbers of $ X $. For complete $ k $- schemes the numbers $ b _ {i} ( X; l) $ are defined and are independent of $ l $( $ l \neq \mathop{\rm char} k $). If $ k $ is an algebraically closed field of characteristic $ p $ and if $ l \neq p $, then the assignment of the spaces $ H _ {l} ^ {i} ( X) $ to a smooth complete $ k $- variety defines a Weil cohomology. If $ k = \mathbf C $ is the field of complex numbers, the comparison theorem $ H _ {l} ^ {i} = H ^ {i} ( X, \mathbf Q ) \otimes \mathbf Q _ {l} $ is valid.
References
| [1] | A. Grothendieck, "Formule de Lefschetz et rationalité des fonctions 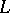 " , Sem. Bourbaki , 17 : 279 (1964–1965) " , Sem. Bourbaki , 17 : 279 (1964–1965) |
Comments
The fact (mentioned above) that for complete $ k $- schemes the Betti numbers are independent of $ l $ follows from Deligne's proof of the Weil conjectures (cf. also Zeta-function).
References
| [a1] | A. Grothendieck, "Cohomologie 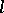 -adique et fonctions -adique et fonctions 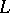 " , SGA 5 , Lect. notes in math. , 589 , Springer (1977) " , SGA 5 , Lect. notes in math. , 589 , Springer (1977) |
| [a2] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) |
| [a3] | E. Freitag, R. Kiehl, "Etale cohomology and the Weil conjectures" , Springer (1988) |
| [a4] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–307 |
| [a5] | P. Deligne, "La conjecture de Weil II" Publ. Math. IHES , 52 (1980) pp. 137–252 |
L-adic-cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-adic-cohomology&oldid=15770