Difference between revisions of "Trigonometric functions"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | The class of elementary functions sine, cosine, tangent, cotangent, secant, cosecant. These are denoted, respectively, by: | + | <!-- |
| + | t0942101.png | ||
| + | $#A+1 = 117 n = 0 | ||
| + | $#C+1 = 117 : ~/encyclopedia/old_files/data/T094/T.0904210 Trigonometric functions | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | The class of elementary functions sine, cosine, tangent, cotangent, secant, cosecant. These are denoted, respectively, by: $ \sin x $, | ||
| + | $ \cos x $, | ||
| + | $ \mathop{\rm tan} x $( | ||
| + | or $ \mathop{\rm tg} x $), | ||
| + | $ \mathop{\rm cot} x $( | ||
| + | or $ \mathop{\rm cotan} x $), | ||
| + | $ \mathop{\rm sec} x $, | ||
| + | $ \mathop{\rm csc} x $( | ||
| + | or $ \cosec x $). | ||
==Trigonometric functions of a real argument.== | ==Trigonometric functions of a real argument.== | ||
| − | Let | + | Let $ \alpha $ |
| + | be a real number. Let $ A = ( x _ \alpha , y _ \alpha ) $ | ||
| + | be the end point of the arc on the unit circle $ x ^ {2} + y ^ {2} = 1 $( | ||
| + | see Fig. a) having initial point $ B = ( 1, 0) $ | ||
| + | and length $ | \alpha | $. | ||
| + | The arc from $ B $ | ||
| + | to $ A $ | ||
| + | is taken in the counter-clockwise direction if $ \alpha \geq 0 $, | ||
| + | and in the clockwise direction if $ \alpha < 0 $. | ||
| + | If $ \alpha = 0 $, | ||
| + | then $ A = B $; | ||
| + | if, e.g., $ \alpha = (- 7 \pi )/ ( 2) $, | ||
| + | then $ A = ( 0, 1) $. | ||
| + | $ B $, | ||
| + | $ | BA | = \alpha > 0 $ | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t094210a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t094210a.gif" /> | ||
| Line 8: | Line 42: | ||
Figure: t094210a | Figure: t094210a | ||
| − | The basic trigonometric functions sine and cosine are defined at | + | The basic trigonometric functions sine and cosine are defined at $ \alpha $ |
| + | by the formulas | ||
| − | + | $$ | |
| + | \sin \alpha = \ | ||
| + | y _ \alpha ,\ \ | ||
| + | \cos \alpha = \ | ||
| + | x _ \alpha . | ||
| + | $$ | ||
The remaining trigonometric functions can be defined by the formulas | The remaining trigonometric functions can be defined by the formulas | ||
| − | + | $$ | |
| + | \mathop{\rm tan} \alpha = \ | ||
| + | |||
| + | \frac{\sin \alpha }{\cos \alpha } | ||
| + | ,\ \ | ||
| + | \mathop{\rm cot} \alpha = \ | ||
| + | |||
| + | \frac{\cos \alpha }{\sin \alpha } | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \mathop{\rm sec} \alpha = { | ||
| + | \frac{1}{\cos \alpha } | ||
| + | } ,\ \ | ||
| + | \mathop{\rm csc} \alpha = { | ||
| + | \frac{1}{\sin \alpha } | ||
| + | } . | ||
| + | $$ | ||
All trigonometric functions are periodic. The graphs of the trigonometric functions are given in Fig. b. | All trigonometric functions are periodic. The graphs of the trigonometric functions are given in Fig. b. | ||
| Line 24: | Line 80: | ||
Figure: t094210b | Figure: t094210b | ||
| − | The main properties of the trigonometric functions — the domain of definition, the range, the parity, and sections of monotonicity — are given in the table below. | + | The main properties of the trigonometric functions — the domain of definition, the range, the parity, and sections of monotonicity — are given in the table below.<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">Function</td> <td colname="2" style="background-color:white;" colspan="1">Domain of definition</td> <td colname="3" style="background-color:white;" colspan="1">Range of values</td> <td colname="4" style="background-color:white;" colspan="1">Parity</td> <td colname="5" style="background-color:white;" colspan="1">Section of monotonicity</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \sin x $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> $ - \infty < x <+ \infty $ | ||
| + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ [- 1, + 1] $ | ||
| + | </td> <td colname="4" style="background-color:white;" colspan="1">Odd</td> <td colname="5" style="background-color:white;" colspan="1"> $ \begin{array}{c} | ||
| + | \textrm{ increases for } x \in (( 4n - 1) \pi /2, ( 4n + 1) \pi /2) \\ | ||
| + | \textrm{ decreases for } x \in (( 4n + 1) \pi /2, ( 4n + 3) \pi /2) | ||
| + | \end{array} | ||
| + | $ | ||
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \cos x $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> $ - \infty < x <+\infty $ | ||
| + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ [- 1, + 1] $ | ||
| + | </td> <td colname="4" style="background-color:white;" colspan="1">Even</td> <td colname="5" style="background-color:white;" colspan="1"> $ \begin{array}{c} | ||
| + | \textrm{ increases for } x \in (( 2n - 1) \pi , 2n \pi) \\ | ||
| + | \textrm{ decreases for } x \in ( 2n \pi , ( 2n + 1) \pi ) | ||
| + | \end{array} | ||
| + | $ | ||
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \mathop{\rm tan} x $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> $ x \neq \pi n + \pi / 2 $ | ||
| + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ (- \infty , + \infty ) $ | ||
| + | </td> <td colname="4" style="background-color:white;" colspan="1">Odd</td> <td colname="5" style="background-color:white;" colspan="1">increases for $ x \in (( 2n - 1) \pi /2, ( 2n + 1) \pi /2) $ | ||
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \mathop{\rm cot} x $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> $ x \neq \pi n $ | ||
| + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ (- \infty , + \infty ) $ | ||
| + | </td> <td colname="4" style="background-color:white;" colspan="1">Odd</td> <td colname="5" style="background-color:white;" colspan="1">decreases for $ x \in ( n \pi , ( n + 1) \pi ) $ | ||
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \mathop{\rm sec} x $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> $ x \neq \pi n + \pi / 2 $ | ||
| + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ (- \infty , - 1 ] \cup [ + 1, + \infty ) $ | ||
| + | </td> <td colname="4" style="background-color:white;" colspan="1">Even</td> <td colname="5" style="background-color:white;" colspan="1"> $ \begin{array}{c} | ||
| + | \textrm{ increases for } x \in ( 2n \pi , ( 2n + 1) \pi ) \\ | ||
| + | \textrm{ decreases for } x \in (( 2n - 1) \pi , 2n \pi ) | ||
| + | \end{array} | ||
| + | $ | ||
| + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ \mathop{\rm csc} x $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> $ x \neq \pi n $ | ||
| + | </td> <td colname="3" style="background-color:white;" colspan="1"> $ (- \infty , - 1 ] \cup [ + 1, + \infty ) $ | ||
| + | </td> <td colname="4" style="background-color:white;" colspan="1">Odd</td> <td colname="5" style="background-color:white;" colspan="1"> $ \begin{array}{c} | ||
| + | \textrm{ increases for } x \in (( 4n + 1) \pi /2, ( 4n + 3) \pi /2) \\ | ||
| + | \textrm{ decreases for } x \in (( 4n - 1) \pi /2, ( 4n + 1) \pi /2) | ||
| + | \end{array} | ||
| + | $ | ||
| + | </td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
| Line 30: | Line 126: | ||
Each trigonometric function is continuous and infinitely differentiable at each point of its domain of definition; the derivatives of the trigonometric functions are: | Each trigonometric function is continuous and infinitely differentiable at each point of its domain of definition; the derivatives of the trigonometric functions are: | ||
| − | + | $$ | |
| + | ( \sin x) ^ \prime = \cos x,\ \ | ||
| + | ( \cos x) ^ \prime = - \sin x, | ||
| + | $$ | ||
| − | + | $$ | |
| + | ( \mathop{\rm tan} x) ^ \prime = { | ||
| + | \frac{1}{\cos ^ {2} x } | ||
| + | } ,\ ( | ||
| + | \mathop{\rm cot} x) ^ \prime = - { | ||
| + | \frac{1}{\sin ^ {2} x } | ||
| + | } . | ||
| + | $$ | ||
The integrals of the trigonometric functions are: | The integrals of the trigonometric functions are: | ||
| − | + | $$ | |
| + | \int\limits \sin x dx = - \cos x + C,\ \ | ||
| + | \int\limits \cos x dx = \sin x + C, | ||
| + | $$ | ||
| − | + | $$ | |
| + | \int\limits \mathop{\rm tan} x dx = - \mathop{\rm ln} | \cos x | + C, | ||
| + | \int\limits \mathop{\rm cot} x dx = \mathop{\rm ln} | \sin x | + C. | ||
| + | $$ | ||
All trigonometric functions have a power series expansion: | All trigonometric functions have a power series expansion: | ||
| − | + | $$ | |
| + | \sin x = x - | ||
| + | |||
| + | \frac{x ^ {3} }{3! } | ||
| + | + | ||
| + | |||
| + | \frac{x ^ {5} }{5! } | ||
| + | - \dots + | ||
| + | (- 1) ^ {n} | ||
| + | |||
| + | \frac{x ^ {2n + 1 } }{( 2n + 1)! } | ||
| + | + \dots | ||
| + | $$ | ||
| − | for < | + | for $ | x | < \infty $; |
| − | + | $$ | |
| + | \cos x = 1 - | ||
| − | + | \frac{x ^ {2} }{2! } | |
| + | + | ||
| − | + | \frac{x ^ {4} }{4! } | |
| + | - | ||
| − | + | \frac{x ^ {6} }{6! } | |
| + | + \dots + | ||
| + | (- 1) ^ {n} | ||
| − | + | \frac{x ^ {2n} }{( 2n)! } | |
| + | + \dots | ||
| + | $$ | ||
| − | < | + | for $ | x | < \infty $; |
| − | + | $$ | |
| + | \mathop{\rm tan} x = \ | ||
| + | x + { | ||
| + | \frac{1}{3} | ||
| + | } | ||
| + | x ^ {3} + { | ||
| + | \frac{2}{15} | ||
| + | } | ||
| + | x ^ {5} + { | ||
| + | \frac{17}{315} | ||
| + | } | ||
| + | x ^ {7} + \dots | ||
| + | $$ | ||
| − | + | $$ | |
| + | \dots | ||
| + | + | ||
| + | \frac{2 ^ {2n} ( 2 ^ {2n} - 1) | B _ {n} | }{( 2n)! } | ||
| + | x ^ {2n - 1 } + \dots | ||
| + | $$ | ||
| − | The function inverse to the function | + | for $ | x | < {\pi / 2 } $; |
| + | |||
| + | $$ | ||
| + | \mathop{\rm cot} x = { | ||
| + | \frac{1}{x} | ||
| + | } - | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | - | ||
| + | \left [ { | ||
| + | \frac{x}{3} | ||
| + | } + | ||
| + | \frac{x ^ {3} }{45 } | ||
| + | + | ||
| + | \frac{2x | ||
| + | ^ {5} }{945 } | ||
| + | + | ||
| + | \frac{x ^ {7} }{4725 } | ||
| + | + \dots + | ||
| + | \frac{2 ^ {2n} | B _ {n} | }{( 2n)! } | ||
| + | x ^ {2n - 1 } + \dots \right ] | ||
| + | $$ | ||
| + | |||
| + | for $ 0 < | x | < \pi $( | ||
| + | the $ B _ {n} $ | ||
| + | are the [[Bernoulli numbers|Bernoulli numbers]]). | ||
| + | |||
| + | The function inverse to the function $ x = \sin y $ | ||
| + | defines $ y $ | ||
| + | as a many-valued function of $ x $, | ||
| + | it is denoted by $ y = \mathop{\rm arc} \sin x $. | ||
| + | The inverse functions of the other trigonometric functions are defined similarly; they are all called [[Inverse trigonometric functions|inverse trigonometric functions]]. | ||
==Trigonometric functions of a complex variable.== | ==Trigonometric functions of a complex variable.== | ||
| − | The trigonometric functions for complex values of the variable | + | The trigonometric functions for complex values of the variable $ z = x + iy $ |
| + | are defined as analytic continuations (cf. [[Analytic continuation|Analytic continuation]]) of the corresponding trigonometric functions of the real variable in the complex plane. | ||
| − | Thus, | + | Thus, $ \sin z $ |
| + | and $ \cos z $ | ||
| + | can be defined by means of the power series for $ \sin x $ | ||
| + | and $ \cos x $ | ||
| + | given above. These series converge in the entire complex plane, therefore $ \sin z $ | ||
| + | and $ \cos z $ | ||
| + | are entire functions (cf. [[Entire function|Entire function]]). | ||
The trigonometric functions tangent and cotangent are defined by the formulas | The trigonometric functions tangent and cotangent are defined by the formulas | ||
| − | + | $$ | |
| + | \mathop{\rm tan} z = \ | ||
| − | The trigonometric functions | + | \frac{\sin z }{\cos z } |
| + | ,\ \ | ||
| + | \mathop{\rm cot} z = \ | ||
| + | |||
| + | \frac{\cos z }{\sin z } | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | The trigonometric functions $ \mathop{\rm tan} z $ | ||
| + | and $ \mathop{\rm cot} z $ | ||
| + | are meromorphic functions (cf. [[Meromorphic function|Meromorphic function]]). The poles of $ \mathop{\rm tan} z $ | ||
| + | are simple (of order one) and are situated at the points $ z = \pi / 2 + \pi n $, | ||
| + | $ n = 0, \pm 1 ,\dots $. | ||
All formulas for the trigonometric functions of a real argument remain true for a complex argument as well. | All formulas for the trigonometric functions of a real argument remain true for a complex argument as well. | ||
| − | In contrast to the trigonometric functions of a real variable, the functions | + | In contrast to the trigonometric functions of a real variable, the functions $ \sin z $ |
| + | and $ \cos z $ | ||
| + | take all complex values: The equations $ \sin z = a $ | ||
| + | and $ \cos z = a $ | ||
| + | each have infinitely many solutions for any complex $ a $: | ||
| − | + | $$ | |
| + | z = \mathop{\rm arc} \sin a = \ | ||
| + | - i \mathop{\rm ln} ( ia \pm \sqrt {1 - a ^ {2} } ), | ||
| + | $$ | ||
| − | + | $$ | |
| + | z = \mathop{\rm arc} \cos a = - i \mathop{\rm ln} ( a \pm \sqrt {a ^ {2} - 1 } ). | ||
| + | $$ | ||
| − | The trigonometric functions | + | The trigonometric functions $ \mathop{\rm tan} z $ |
| + | and $ \mathop{\rm cot} z $ | ||
| + | take all complex values except $ \pm i $: | ||
| + | The equations $ \mathop{\rm tan} z = a $, | ||
| + | $ \mathop{\rm cot} z = a $ | ||
| + | each have infinitely many solutions for any complex number $ a \neq \pm i $: | ||
| − | + | $$ | |
| + | z = \mathop{\rm arc} \mathop{\rm tan} a = \ | ||
| + | { | ||
| + | \frac{i}{2} | ||
| + | } \mathop{\rm ln} | ||
| + | \frac{1 - ia }{1 + ia } | ||
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | z = \mathop{\rm arc} \mathop{\rm cot} a = { | ||
| + | \frac{i}{2} | ||
| + | } \mathop{\rm ln} | ||
| + | \frac{ia + 1 }{ia - 1 } | ||
| + | . | ||
| + | $$ | ||
The trigonometric functions can be expressed in terms of the [[Exponential function|exponential function]]: | The trigonometric functions can be expressed in terms of the [[Exponential function|exponential function]]: | ||
| − | + | $$ | |
| + | \sin z = { | ||
| + | \frac{1}{2i} | ||
| + | } ( e ^ {iz} - e ^ {-} iz ), | ||
| + | $$ | ||
| − | + | $$ | |
| + | \cos z = { | ||
| + | \frac{1}{2} | ||
| + | } ( e ^ {iz} + e ^ {-} iz ),\ \ | ||
| + | \mathop{\rm tan} z = { | ||
| + | \frac{1}{i} | ||
| + | } | ||
| + | \frac{e ^ {iz} - e ^ {-} iz }{e ^ {iz} + e ^ {-} iz } | ||
| + | , | ||
| + | $$ | ||
and the [[Hyperbolic functions|hyperbolic functions]]: | and the [[Hyperbolic functions|hyperbolic functions]]: | ||
| − | + | $$ | |
| − | + | \sin z = - i \sinh iz,\ \ | |
| − | + | \cos z = \cosh iz,\ \ | |
| + | \mathop{\rm tan} z = - i \mathop{\rm tanh} iz. | ||
| + | $$ | ||
====Comments==== | ====Comments==== | ||
The trigonometric functions are also called circular functions. | The trigonometric functions are also called circular functions. | ||
| − | A formal definition of | + | A formal definition of $ \sin z $ |
| + | and $ \cos z $( | ||
| + | independent of a picture) can be given by power series and as follows. First of all it can easily be proved that from the previous, visual definition of $ \sin x $ | ||
| + | and $ \cos x $ | ||
| + | follows: | ||
| − | + | $$ | |
| + | \mathop{\rm arc} \sin x = \int\limits _ { 0 } ^ { x } | ||
| + | \frac{dx}{\sqrt {1- t ^ {2} } } | ||
| + | . | ||
| + | $$ | ||
| − | This can be taken as a formal definition of | + | This can be taken as a formal definition of $ \mathop{\rm arc} \sin x $ |
| + | and the inverse function of $ \mathop{\rm arc} \sin x $ | ||
| + | can be taken as a formal definition of $ \sin x $. | ||
| − | If | + | If $ z $ |
| + | is a complex number $ x + iy $, | ||
| + | with real $ x $ | ||
| + | and $ y $, | ||
| + | one can define $ e ^ {z} = e ^ {x} ( \cos y + i \sin y ) $, | ||
| + | and then for complex $ z $ | ||
| + | define: | ||
| − | + | $$ | |
| + | \sin z = | ||
| + | \frac{e ^ {iz} - e ^ {-} iz }{2i} | ||
| + | ,\ \ | ||
| + | \cos z = | ||
| + | \frac{e ^ {iz} + e ^ {-} iz }{2} | ||
| + | . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.M. Apostol, "Calculus" , '''I''' , Blaisdell (1967)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.R.F. Verhey, "Complex variables and applications" , McGraw-Hill (1974)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.M. Apostol, "Calculus" , '''I''' , Blaisdell (1967)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.R.F. Verhey, "Complex variables and applications" , McGraw-Hill (1974)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972)</TD></TR></table> | ||
Latest revision as of 08:26, 6 June 2020
The class of elementary functions sine, cosine, tangent, cotangent, secant, cosecant. These are denoted, respectively, by: $ \sin x $,
$ \cos x $,
$ \mathop{\rm tan} x $(
or $ \mathop{\rm tg} x $),
$ \mathop{\rm cot} x $(
or $ \mathop{\rm cotan} x $),
$ \mathop{\rm sec} x $,
$ \mathop{\rm csc} x $(
or $ \cosec x $).
Trigonometric functions of a real argument.
Let $ \alpha $ be a real number. Let $ A = ( x _ \alpha , y _ \alpha ) $ be the end point of the arc on the unit circle $ x ^ {2} + y ^ {2} = 1 $( see Fig. a) having initial point $ B = ( 1, 0) $ and length $ | \alpha | $. The arc from $ B $ to $ A $ is taken in the counter-clockwise direction if $ \alpha \geq 0 $, and in the clockwise direction if $ \alpha < 0 $. If $ \alpha = 0 $, then $ A = B $; if, e.g., $ \alpha = (- 7 \pi )/ ( 2) $, then $ A = ( 0, 1) $. $ B $, $ | BA | = \alpha > 0 $

Figure: t094210a
The basic trigonometric functions sine and cosine are defined at $ \alpha $ by the formulas
$$ \sin \alpha = \ y _ \alpha ,\ \ \cos \alpha = \ x _ \alpha . $$
The remaining trigonometric functions can be defined by the formulas
$$ \mathop{\rm tan} \alpha = \ \frac{\sin \alpha }{\cos \alpha } ,\ \ \mathop{\rm cot} \alpha = \ \frac{\cos \alpha }{\sin \alpha } , $$
$$ \mathop{\rm sec} \alpha = { \frac{1}{\cos \alpha } } ,\ \ \mathop{\rm csc} \alpha = { \frac{1}{\sin \alpha } } . $$
All trigonometric functions are periodic. The graphs of the trigonometric functions are given in Fig. b.
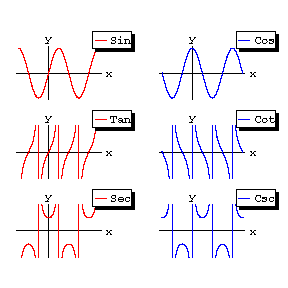
Figure: t094210b
The main properties of the trigonometric functions — the domain of definition, the range, the parity, and sections of monotonicity — are given in the table below.
<tbody> </tbody>
|
Each trigonometric function is continuous and infinitely differentiable at each point of its domain of definition; the derivatives of the trigonometric functions are:
$$ ( \sin x) ^ \prime = \cos x,\ \ ( \cos x) ^ \prime = - \sin x, $$
$$ ( \mathop{\rm tan} x) ^ \prime = { \frac{1}{\cos ^ {2} x } } ,\ ( \mathop{\rm cot} x) ^ \prime = - { \frac{1}{\sin ^ {2} x } } . $$
The integrals of the trigonometric functions are:
$$ \int\limits \sin x dx = - \cos x + C,\ \ \int\limits \cos x dx = \sin x + C, $$
$$ \int\limits \mathop{\rm tan} x dx = - \mathop{\rm ln} | \cos x | + C, \int\limits \mathop{\rm cot} x dx = \mathop{\rm ln} | \sin x | + C. $$
All trigonometric functions have a power series expansion:
$$ \sin x = x - \frac{x ^ {3} }{3! } + \frac{x ^ {5} }{5! } - \dots + (- 1) ^ {n} \frac{x ^ {2n + 1 } }{( 2n + 1)! } + \dots $$
for $ | x | < \infty $;
$$ \cos x = 1 - \frac{x ^ {2} }{2! } + \frac{x ^ {4} }{4! } - \frac{x ^ {6} }{6! } + \dots + (- 1) ^ {n} \frac{x ^ {2n} }{( 2n)! } + \dots $$
for $ | x | < \infty $;
$$ \mathop{\rm tan} x = \ x + { \frac{1}{3} } x ^ {3} + { \frac{2}{15} } x ^ {5} + { \frac{17}{315} } x ^ {7} + \dots $$
$$ \dots + \frac{2 ^ {2n} ( 2 ^ {2n} - 1) | B _ {n} | }{( 2n)! } x ^ {2n - 1 } + \dots $$
for $ | x | < {\pi / 2 } $;
$$ \mathop{\rm cot} x = { \frac{1}{x} } - $$
$$ - \left [ { \frac{x}{3} } + \frac{x ^ {3} }{45 } + \frac{2x ^ {5} }{945 } + \frac{x ^ {7} }{4725 } + \dots + \frac{2 ^ {2n} | B _ {n} | }{( 2n)! } x ^ {2n - 1 } + \dots \right ] $$
for $ 0 < | x | < \pi $( the $ B _ {n} $ are the Bernoulli numbers).
The function inverse to the function $ x = \sin y $ defines $ y $ as a many-valued function of $ x $, it is denoted by $ y = \mathop{\rm arc} \sin x $. The inverse functions of the other trigonometric functions are defined similarly; they are all called inverse trigonometric functions.
Trigonometric functions of a complex variable.
The trigonometric functions for complex values of the variable $ z = x + iy $ are defined as analytic continuations (cf. Analytic continuation) of the corresponding trigonometric functions of the real variable in the complex plane.
Thus, $ \sin z $ and $ \cos z $ can be defined by means of the power series for $ \sin x $ and $ \cos x $ given above. These series converge in the entire complex plane, therefore $ \sin z $ and $ \cos z $ are entire functions (cf. Entire function).
The trigonometric functions tangent and cotangent are defined by the formulas
$$ \mathop{\rm tan} z = \ \frac{\sin z }{\cos z } ,\ \ \mathop{\rm cot} z = \ \frac{\cos z }{\sin z } . $$
The trigonometric functions $ \mathop{\rm tan} z $ and $ \mathop{\rm cot} z $ are meromorphic functions (cf. Meromorphic function). The poles of $ \mathop{\rm tan} z $ are simple (of order one) and are situated at the points $ z = \pi / 2 + \pi n $, $ n = 0, \pm 1 ,\dots $.
All formulas for the trigonometric functions of a real argument remain true for a complex argument as well.
In contrast to the trigonometric functions of a real variable, the functions $ \sin z $ and $ \cos z $ take all complex values: The equations $ \sin z = a $ and $ \cos z = a $ each have infinitely many solutions for any complex $ a $:
$$ z = \mathop{\rm arc} \sin a = \ - i \mathop{\rm ln} ( ia \pm \sqrt {1 - a ^ {2} } ), $$
$$ z = \mathop{\rm arc} \cos a = - i \mathop{\rm ln} ( a \pm \sqrt {a ^ {2} - 1 } ). $$
The trigonometric functions $ \mathop{\rm tan} z $ and $ \mathop{\rm cot} z $ take all complex values except $ \pm i $: The equations $ \mathop{\rm tan} z = a $, $ \mathop{\rm cot} z = a $ each have infinitely many solutions for any complex number $ a \neq \pm i $:
$$ z = \mathop{\rm arc} \mathop{\rm tan} a = \ { \frac{i}{2} } \mathop{\rm ln} \frac{1 - ia }{1 + ia } , $$
$$ z = \mathop{\rm arc} \mathop{\rm cot} a = { \frac{i}{2} } \mathop{\rm ln} \frac{ia + 1 }{ia - 1 } . $$
The trigonometric functions can be expressed in terms of the exponential function:
$$ \sin z = { \frac{1}{2i} } ( e ^ {iz} - e ^ {-} iz ), $$
$$ \cos z = { \frac{1}{2} } ( e ^ {iz} + e ^ {-} iz ),\ \ \mathop{\rm tan} z = { \frac{1}{i} } \frac{e ^ {iz} - e ^ {-} iz }{e ^ {iz} + e ^ {-} iz } , $$
and the hyperbolic functions:
$$ \sin z = - i \sinh iz,\ \ \cos z = \cosh iz,\ \ \mathop{\rm tan} z = - i \mathop{\rm tanh} iz. $$
Comments
The trigonometric functions are also called circular functions.
A formal definition of $ \sin z $ and $ \cos z $( independent of a picture) can be given by power series and as follows. First of all it can easily be proved that from the previous, visual definition of $ \sin x $ and $ \cos x $ follows:
$$ \mathop{\rm arc} \sin x = \int\limits _ { 0 } ^ { x } \frac{dx}{\sqrt {1- t ^ {2} } } . $$
This can be taken as a formal definition of $ \mathop{\rm arc} \sin x $ and the inverse function of $ \mathop{\rm arc} \sin x $ can be taken as a formal definition of $ \sin x $.
If $ z $ is a complex number $ x + iy $, with real $ x $ and $ y $, one can define $ e ^ {z} = e ^ {x} ( \cos y + i \sin y ) $, and then for complex $ z $ define:
$$ \sin z = \frac{e ^ {iz} - e ^ {-} iz }{2i} ,\ \ \cos z = \frac{e ^ {iz} + e ^ {-} iz }{2} . $$
References
| [a1] | T.M. Apostol, "Calculus" , I , Blaisdell (1967) |
| [a2] | A.R.F. Verhey, "Complex variables and applications" , McGraw-Hill (1974) |
| [a3] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) |
Trigonometric functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trigonometric_functions&oldid=14919