Difference between revisions of "Stability in game theory"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s0869702.png | ||
| + | $#A+1 = 85 n = 1 | ||
| + | $#C+1 = 85 : ~/encyclopedia/old_files/data/S086/S.0806970 Stability in game theory | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A principle reflecting directly or indirectly the idea of stability of a situation (or of a set of situations). One singles out the following basic concepts of stability. | A principle reflecting directly or indirectly the idea of stability of a situation (or of a set of situations). One singles out the following basic concepts of stability. | ||
| − | 1) | + | 1) $ \phi $- |
| + | stability, cf. [[Coalitional game|Coalitional game]]. | ||
| − | 2) | + | 2) $ \psi $- |
| + | stability. An optimality principle in a [[Cooperative game|cooperative game]], connected with the concept of stability of pairs, consisting of a partition of the set $ I $ | ||
| + | of players into coalitions and allocations relative to the formation of new coalitions. A partition $ {\mathcal T} = ( T _ {1} \dots T _ {m} ) $ | ||
| + | of the set $ I $ | ||
| + | of players is called a coalition structure. Let $ \langle I, v \rangle $ | ||
| + | be a cooperative game and $ \psi $ | ||
| + | a function associating with every coalition structure $ {\mathcal T} $ | ||
| + | a set of coalitions $ \psi ( {\mathcal T} ) $. | ||
| + | A pair $ ( x, {\mathcal T} ) $, | ||
| + | where $ x $ | ||
| + | is an allocation, is called $ \psi $- | ||
| + | stable if $ \sum _ {i \in S } x _ {i} \geq v ( S) $ | ||
| + | for all $ S \in \psi ( {\mathcal T} ) $ | ||
| + | and if $ x _ {i} > v ( \{ i \} ) $ | ||
| + | when $ \{ i \} \notin {\mathcal T} $. | ||
| − | 3) | + | 3) $ k $- |
| + | stability. A special case of $ \psi $- | ||
| + | stability, when for $ \psi ( {\mathcal T} ) $ | ||
| + | a set of coalitions is chosen, each of which differs from any element of $ {\mathcal T} $ | ||
| + | by not more than $ k $ | ||
| + | players. | ||
| − | 4) | + | 4) $ M $- |
| + | stability. An optimality principle in the theory of cooperative games which formalizes the intuitive notion of stability of formation of coalitions and allocation of values $ v ( T) $ | ||
| + | of a characteristic function $ v $ | ||
| + | defined on the set of coalitions $ T $ | ||
| + | relative to the possible threat of one coalition against the others. A pair $ ( x, {\mathcal T} ) $, | ||
| + | where $ x = ( x _ {i} ) _ {i \in I } $ | ||
| + | is a vector satisfying the condition $ \sum _ {i \in T _ {k} } x _ {i} = v ( T _ {k} ) $, | ||
| + | $ k = 1 \dots m $, | ||
| + | while $ {\mathcal T} = ( T _ {1} \dots T _ {m} ) $ | ||
| + | is a coalition structure, is called a configuration. A configuration is said to be individually rational if $ x _ {i} \geq v ( \{ i \} ) $, | ||
| + | $ i \in I $. | ||
| + | A configuration $ ( x, {\mathcal T} ) $ | ||
| + | is called coalitionally rational if the vector $ x $ | ||
| + | satisfies $ \sum _ {i \in S } x _ {i} \geq v ( S) $ | ||
| + | for any coalition $ S \subset T _ {k} $, | ||
| + | $ k = 1 \dots m $. | ||
| + | In case $ \sum _ {k = 1 } ^ {m} v ( T _ {k} ) = v ( I) $, | ||
| + | in particular when $ {\mathcal T} = \{ I \} $, | ||
| + | for every individually rational configuration $ ( x, {\mathcal T} ) $ | ||
| + | the vector $ x $ | ||
| + | is an allocation. | ||
| − | The set | + | The set $ P ( K; {\mathcal T} ) = \{ {i \in I } : {i \in T _ {k} \textrm{ and } T _ {k} \cap K \neq \emptyset } \} $ |
| + | is called the set of partners of a coalition $ K \subset I $ | ||
| + | in a coalition structure $ {\mathcal T} $. | ||
| + | Let $ ( x, {\mathcal T} ) $ | ||
| + | be a coalitionally rational configuration and let $ K, L \subset I $ | ||
| + | be disjoint coalitions. A coalitionally rational configuration $ ( y, U) $ | ||
| + | satisfying the conditions | ||
| − | + | $$ | |
| + | P ( K; U) \cap L = \emptyset , | ||
| + | $$ | ||
| − | + | $$ | |
| + | y _ {i} > x _ {i} \ \textrm{ for } \textrm{ all } i \in K, | ||
| + | $$ | ||
| − | + | $$ | |
| + | y _ {i} \geq x _ {i} \ \textrm{ for } \textrm{ all } i \in P ( K; U), | ||
| + | $$ | ||
| − | is called a threat of a coalition | + | is called a threat of a coalition $ K $ |
| + | against $ L $. | ||
| + | By a counter-threat of $ L $ | ||
| + | against $ K $ | ||
| + | one understands a coalitionally rational configuration $ ( z, V) $ | ||
| + | satisfying the conditions | ||
| − | + | $$ | |
| + | K \subset \setminus P ( L; V), | ||
| + | $$ | ||
| − | + | $$ | |
| + | z _ {i} \geq x _ {i} \ \textrm{ for } \textrm{ all } i \in P ( L; V), | ||
| + | $$ | ||
| − | + | $$ | |
| + | z _ {i} \geq y _ {i} \ \textrm{ for } \textrm{ all } i \in P ( L; V) \cap P ( K; U). | ||
| + | $$ | ||
| − | A coalitionally rational configuration | + | A coalitionally rational configuration $ ( x, {\mathcal T} ) $ |
| + | is called $ M $- | ||
| + | stable if for any pair of disjoint coalitions $ K, L $ | ||
| + | and for every threat of $ K $ | ||
| + | against $ L $ | ||
| + | there is a counter-threat of $ L $ | ||
| + | against $ K $. | ||
| + | The set of all $ M $- | ||
| + | stable configurations for a coalition structure $ {\mathcal T} $ | ||
| + | is called the $ M $- | ||
| + | stable set and is denoted by $ M $ | ||
| + | or $ M ( {\mathcal T} ) $. | ||
| + | In the case $ \sum _ {k} v ( T _ {k} ) = v ( I) $, | ||
| + | the set $ M $ | ||
| + | contains the core (cf. [[Core in the theory of games|Core in the theory of games]]) of the cooperative game $ \langle I, v \rangle $. | ||
| + | The set $ M $ | ||
| + | often turns out to be empty, and therefore one considers further the set $ M _ {1} ^ {(} i) $ | ||
| + | which is defined analogously to $ M $, | ||
| + | with the following changes: one considers not only coalitionally rational configurations, but all individually rational configurations admitting only threats and counter-threats among one-element coalitions, i.e. between individual players. It can be proved that the set $ M _ {1} ^ {(} i) $ | ||
| + | is non-empty for any coalition structure. The set $ M _ {1} ^ {(} i) $ | ||
| + | for $ {\mathcal T} = \{ I \} $ | ||
| + | contains the $ k $- | ||
| + | kernel and coincides with it and the core for a [[Convex game|convex game]] $ \langle I, v \rangle $. | ||
| − | The concepts of | + | The concepts of $ M $- |
| + | stability and $ M _ {1} ^ {(} i) $- | ||
| + | stability have a natural generalization to cooperative games without side payments. It is known that in this case the set $ M _ {1} ^ {(} i) $ | ||
| + | may be empty; there are certain conditions for $ M _ {1} ^ {(} i) $ | ||
| + | to be non-empty. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.J. Aumann, M. Maschler, "The bargaining set for cooperative games" , ''Advances in game theory'' , Princeton Univ. Press pp. 443–476</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.N. Vorob'ev, "The present state of the theory of games" ''Russian Math. Surveys'' , '''25''' : 2 (1970) pp. 77–150 ''Uspekhi Mat. Nauk'' , '''25''' : 2 (1970) pp. 81–140</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.D. Luce, , ''Mathematical Models of Human Behaviour'' , Stanford (1955) pp. 32–44</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.D. Luce, H. Raiffa, "Games and decisions. Introduction and critical survey" , Wiley (1957)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Peleg, "Existence theorem for the bargaining of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086970/s08697092.png" />" ''Bull. Amer. Math. Soc.'' , '''69''' (1963) pp. 109–110</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Peleg, "Quota games with a continuum of players" ''Israel J. Math.'' , '''1''' (1963) pp. 48–53</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G. Owen, "The theory of games" , Acad. Press (1982)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.J. Aumann, M. Maschler, "The bargaining set for cooperative games" , ''Advances in game theory'' , Princeton Univ. Press pp. 443–476</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.N. Vorob'ev, "The present state of the theory of games" ''Russian Math. Surveys'' , '''25''' : 2 (1970) pp. 77–150 ''Uspekhi Mat. Nauk'' , '''25''' : 2 (1970) pp. 81–140</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.D. Luce, , ''Mathematical Models of Human Behaviour'' , Stanford (1955) pp. 32–44</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.D. Luce, H. Raiffa, "Games and decisions. Introduction and critical survey" , Wiley (1957)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Peleg, "Existence theorem for the bargaining of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086970/s08697092.png" />" ''Bull. Amer. Math. Soc.'' , '''69''' (1963) pp. 109–110</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B. Peleg, "Quota games with a continuum of players" ''Israel J. Math.'' , '''1''' (1963) pp. 48–53</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G. Owen, "The theory of games" , Acad. Press (1982)</TD></TR></table> | ||
Revision as of 08:22, 6 June 2020
A principle reflecting directly or indirectly the idea of stability of a situation (or of a set of situations). One singles out the following basic concepts of stability.
1) $ \phi $- stability, cf. Coalitional game.
2) $ \psi $- stability. An optimality principle in a cooperative game, connected with the concept of stability of pairs, consisting of a partition of the set $ I $ of players into coalitions and allocations relative to the formation of new coalitions. A partition $ {\mathcal T} = ( T _ {1} \dots T _ {m} ) $ of the set $ I $ of players is called a coalition structure. Let $ \langle I, v \rangle $ be a cooperative game and $ \psi $ a function associating with every coalition structure $ {\mathcal T} $ a set of coalitions $ \psi ( {\mathcal T} ) $. A pair $ ( x, {\mathcal T} ) $, where $ x $ is an allocation, is called $ \psi $- stable if $ \sum _ {i \in S } x _ {i} \geq v ( S) $ for all $ S \in \psi ( {\mathcal T} ) $ and if $ x _ {i} > v ( \{ i \} ) $ when $ \{ i \} \notin {\mathcal T} $.
3) $ k $- stability. A special case of $ \psi $- stability, when for $ \psi ( {\mathcal T} ) $ a set of coalitions is chosen, each of which differs from any element of $ {\mathcal T} $ by not more than $ k $ players.
4) $ M $- stability. An optimality principle in the theory of cooperative games which formalizes the intuitive notion of stability of formation of coalitions and allocation of values $ v ( T) $ of a characteristic function $ v $ defined on the set of coalitions $ T $ relative to the possible threat of one coalition against the others. A pair $ ( x, {\mathcal T} ) $, where $ x = ( x _ {i} ) _ {i \in I } $ is a vector satisfying the condition $ \sum _ {i \in T _ {k} } x _ {i} = v ( T _ {k} ) $, $ k = 1 \dots m $, while $ {\mathcal T} = ( T _ {1} \dots T _ {m} ) $ is a coalition structure, is called a configuration. A configuration is said to be individually rational if $ x _ {i} \geq v ( \{ i \} ) $, $ i \in I $. A configuration $ ( x, {\mathcal T} ) $ is called coalitionally rational if the vector $ x $ satisfies $ \sum _ {i \in S } x _ {i} \geq v ( S) $ for any coalition $ S \subset T _ {k} $, $ k = 1 \dots m $. In case $ \sum _ {k = 1 } ^ {m} v ( T _ {k} ) = v ( I) $, in particular when $ {\mathcal T} = \{ I \} $, for every individually rational configuration $ ( x, {\mathcal T} ) $ the vector $ x $ is an allocation.
The set $ P ( K; {\mathcal T} ) = \{ {i \in I } : {i \in T _ {k} \textrm{ and } T _ {k} \cap K \neq \emptyset } \} $ is called the set of partners of a coalition $ K \subset I $ in a coalition structure $ {\mathcal T} $. Let $ ( x, {\mathcal T} ) $ be a coalitionally rational configuration and let $ K, L \subset I $ be disjoint coalitions. A coalitionally rational configuration $ ( y, U) $ satisfying the conditions
$$ P ( K; U) \cap L = \emptyset , $$
$$ y _ {i} > x _ {i} \ \textrm{ for } \textrm{ all } i \in K, $$
$$ y _ {i} \geq x _ {i} \ \textrm{ for } \textrm{ all } i \in P ( K; U), $$
is called a threat of a coalition $ K $ against $ L $. By a counter-threat of $ L $ against $ K $ one understands a coalitionally rational configuration $ ( z, V) $ satisfying the conditions
$$ K \subset \setminus P ( L; V), $$
$$ z _ {i} \geq x _ {i} \ \textrm{ for } \textrm{ all } i \in P ( L; V), $$
$$ z _ {i} \geq y _ {i} \ \textrm{ for } \textrm{ all } i \in P ( L; V) \cap P ( K; U). $$
A coalitionally rational configuration $ ( x, {\mathcal T} ) $ is called $ M $- stable if for any pair of disjoint coalitions $ K, L $ and for every threat of $ K $ against $ L $ there is a counter-threat of $ L $ against $ K $. The set of all $ M $- stable configurations for a coalition structure $ {\mathcal T} $ is called the $ M $- stable set and is denoted by $ M $ or $ M ( {\mathcal T} ) $. In the case $ \sum _ {k} v ( T _ {k} ) = v ( I) $, the set $ M $ contains the core (cf. Core in the theory of games) of the cooperative game $ \langle I, v \rangle $. The set $ M $ often turns out to be empty, and therefore one considers further the set $ M _ {1} ^ {(} i) $ which is defined analogously to $ M $, with the following changes: one considers not only coalitionally rational configurations, but all individually rational configurations admitting only threats and counter-threats among one-element coalitions, i.e. between individual players. It can be proved that the set $ M _ {1} ^ {(} i) $ is non-empty for any coalition structure. The set $ M _ {1} ^ {(} i) $ for $ {\mathcal T} = \{ I \} $ contains the $ k $- kernel and coincides with it and the core for a convex game $ \langle I, v \rangle $.
The concepts of $ M $- stability and $ M _ {1} ^ {(} i) $- stability have a natural generalization to cooperative games without side payments. It is known that in this case the set $ M _ {1} ^ {(} i) $ may be empty; there are certain conditions for $ M _ {1} ^ {(} i) $ to be non-empty.
References
| [1] | R.J. Aumann, M. Maschler, "The bargaining set for cooperative games" , Advances in game theory , Princeton Univ. Press pp. 443–476 |
| [2] | N.N. Vorob'ev, "The present state of the theory of games" Russian Math. Surveys , 25 : 2 (1970) pp. 77–150 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 81–140 |
| [3] | R.D. Luce, , Mathematical Models of Human Behaviour , Stanford (1955) pp. 32–44 |
| [4] | R.D. Luce, H. Raiffa, "Games and decisions. Introduction and critical survey" , Wiley (1957) |
| [5] | B. Peleg, "Existence theorem for the bargaining of 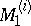 " Bull. Amer. Math. Soc. , 69 (1963) pp. 109–110 " Bull. Amer. Math. Soc. , 69 (1963) pp. 109–110 |
| [6] | B. Peleg, "Quota games with a continuum of players" Israel J. Math. , 1 (1963) pp. 48–53 |
| [7] | G. Owen, "The theory of games" , Acad. Press (1982) |
Stability in game theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_in_game_theory&oldid=14883