Difference between revisions of "Porosity point"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0738301.png | ||
| + | $#A+1 = 45 n = 6 | ||
| + | $#C+1 = 45 : ~/encyclopedia/old_files/data/P073/P.0703830 Porosity point | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | Sometimes, in the case of an infinite-dimensional space | + | ''of a set $ E $ |
| + | in a metric space $ X $'' | ||
| + | |||
| + | A point $ x _ {0} \in X $ | ||
| + | for which there exists a sequence of open balls $ B _ {k} $ | ||
| + | with radii $ r _ {k} \rightarrow 0 $ | ||
| + | and common centre at the point $ x _ {0} $, | ||
| + | such that for any $ k = 1 , 2 \dots $ | ||
| + | there is an open ball $ G _ {k} \subset B _ {k} \setminus E $ | ||
| + | with radius $ \rho _ {k} \geq C r _ {k} $, | ||
| + | where $ C $ | ||
| + | is positive and independent of $ k $( | ||
| + | but, generally speaking, depends on $ x _ {0} $ | ||
| + | and $ E $). | ||
| + | A set $ E $ | ||
| + | is called porous if any point in it is a porosity point of it. A set $ E $ | ||
| + | is called $ \sigma $- | ||
| + | porous if it can be represented as a finite or countable union of porous sets (see [[#References|[1]]]). A porosity point of $ E $ | ||
| + | is a porosity point of its closure $ \overline{E}\; $. | ||
| + | If $ X = \mathbf R ^ {n} $, | ||
| + | a porosity point of a set $ E \subset X $ | ||
| + | is not a Lebesgue density point either of $ E $ | ||
| + | or of $ \overline{E}\; $. | ||
| + | Any porous or $ \sigma $- | ||
| + | porous set $ E \subset \mathbf R ^ {n} $ | ||
| + | is of the first Baire category (cf. [[Baire classes|Baire classes]]) and of Lebesgue measure zero in $ \mathbf R ^ {n} $. | ||
| + | The converse of this statement, generally speaking, does not hold: There even exist nowhere-dense perfect sets $ E \subset \mathbf R ^ {1} $ | ||
| + | of measure zero that are not $ \sigma $- | ||
| + | porous (see [[#References|[2]]]). | ||
| + | |||
| + | Sometimes, in the case of an infinite-dimensional space $ X $, | ||
| + | porous and $ \sigma $- | ||
| + | porous sets take the role of sets of measure zero. If $ X = \mathbf R ^ {n} $ | ||
| + | and $ h: [ 0, \infty ) \rightarrow \mathbf R $ | ||
| + | is an increasing continuous function with $ h( 0) = 0 $, | ||
| + | then $ x _ {0} \in X $ | ||
| + | is called an $ h $- | ||
| + | porous point of a set $ E \subset X $ | ||
| + | if $ h ( \rho _ {k} ) \geq Cr _ {k} $, | ||
| + | using the same notations ( $ C $ | ||
| + | is independent of $ k $). | ||
| + | The concepts of $ h $- | ||
| + | porous and $ \sigma $- | ||
| + | $ h $- | ||
| + | porous sets are defined accordingly. In the case $ h( t)/t \rightarrow \infty $( | ||
| + | $ t \rightarrow 0 $), | ||
| + | a $ h $- | ||
| + | porous set $ E \subset X = \mathbf R ^ {n} $ | ||
| + | may be a set of positive Lebesgue measure. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.P. Dolzhenko, "Boundary properties of arbitrary functions" ''Math. USSR Izv.'' , '''1''' : 1 (1967) pp. 1–12 ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''31''' : 1 (1967) pp. 3–14</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L. Zajiček, "Sets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383051.png" />-porosity and sets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383052.png" />-porosity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383053.png" />" ''Casopis. Pešt. Mat.'' , '''101''' (1976) pp. 350–359</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Foran, P.D. Humke, "Some set-theoretic properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383054.png" />-porous sets" ''Real Anal. Exch.'' , '''6''' : 1 (1980/81) pp. 114–119</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Tkadlec, "Constructions of some non-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383055.png" />-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383056.png" />-porous sets on the real line" ''Real Anal. Exch.'' , '''9''' : 2 (1983/84) pp. 473–482</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S.J. Agronsky, A.M. Bruckner, "Local compactness and porosity in metric spaces" ''Real Anal. Exch.'' , '''11''' : 2 (1985/86) pp. 365–379</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> Yu.A. Shevchenko, "On Vitali's covering theorem" ''Vestnik Moskov. Univ. Ser. 1. Mat. Mech.'' : 3 (1989) pp. 11–14 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.P. Dolzhenko, "Boundary properties of arbitrary functions" ''Math. USSR Izv.'' , '''1''' : 1 (1967) pp. 1–12 ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''31''' : 1 (1967) pp. 3–14</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L. Zajiček, "Sets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383051.png" />-porosity and sets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383052.png" />-porosity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383053.png" />" ''Casopis. Pešt. Mat.'' , '''101''' (1976) pp. 350–359</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Foran, P.D. Humke, "Some set-theoretic properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383054.png" />-porous sets" ''Real Anal. Exch.'' , '''6''' : 1 (1980/81) pp. 114–119</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Tkadlec, "Constructions of some non-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383055.png" />-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073830/p07383056.png" />-porous sets on the real line" ''Real Anal. Exch.'' , '''9''' : 2 (1983/84) pp. 473–482</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S.J. Agronsky, A.M. Bruckner, "Local compactness and porosity in metric spaces" ''Real Anal. Exch.'' , '''11''' : 2 (1985/86) pp. 365–379</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> Yu.A. Shevchenko, "On Vitali's covering theorem" ''Vestnik Moskov. Univ. Ser. 1. Mat. Mech.'' : 3 (1989) pp. 11–14 (In Russian)</TD></TR></table> | ||
Latest revision as of 08:07, 6 June 2020
of a set $ E $
in a metric space $ X $
A point $ x _ {0} \in X $ for which there exists a sequence of open balls $ B _ {k} $ with radii $ r _ {k} \rightarrow 0 $ and common centre at the point $ x _ {0} $, such that for any $ k = 1 , 2 \dots $ there is an open ball $ G _ {k} \subset B _ {k} \setminus E $ with radius $ \rho _ {k} \geq C r _ {k} $, where $ C $ is positive and independent of $ k $( but, generally speaking, depends on $ x _ {0} $ and $ E $). A set $ E $ is called porous if any point in it is a porosity point of it. A set $ E $ is called $ \sigma $- porous if it can be represented as a finite or countable union of porous sets (see [1]). A porosity point of $ E $ is a porosity point of its closure $ \overline{E}\; $. If $ X = \mathbf R ^ {n} $, a porosity point of a set $ E \subset X $ is not a Lebesgue density point either of $ E $ or of $ \overline{E}\; $. Any porous or $ \sigma $- porous set $ E \subset \mathbf R ^ {n} $ is of the first Baire category (cf. Baire classes) and of Lebesgue measure zero in $ \mathbf R ^ {n} $. The converse of this statement, generally speaking, does not hold: There even exist nowhere-dense perfect sets $ E \subset \mathbf R ^ {1} $ of measure zero that are not $ \sigma $- porous (see [2]).
Sometimes, in the case of an infinite-dimensional space $ X $, porous and $ \sigma $- porous sets take the role of sets of measure zero. If $ X = \mathbf R ^ {n} $ and $ h: [ 0, \infty ) \rightarrow \mathbf R $ is an increasing continuous function with $ h( 0) = 0 $, then $ x _ {0} \in X $ is called an $ h $- porous point of a set $ E \subset X $ if $ h ( \rho _ {k} ) \geq Cr _ {k} $, using the same notations ( $ C $ is independent of $ k $). The concepts of $ h $- porous and $ \sigma $- $ h $- porous sets are defined accordingly. In the case $ h( t)/t \rightarrow \infty $( $ t \rightarrow 0 $), a $ h $- porous set $ E \subset X = \mathbf R ^ {n} $ may be a set of positive Lebesgue measure.
References
| [1] | E.P. Dolzhenko, "Boundary properties of arbitrary functions" Math. USSR Izv. , 1 : 1 (1967) pp. 1–12 Izv. Akad. Nauk. SSSR Ser. Mat. , 31 : 1 (1967) pp. 3–14 |
| [2] | L. Zajiček, "Sets of 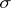 -porosity and sets of -porosity and sets of 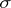 -porosity -porosity 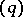 " Casopis. Pešt. Mat. , 101 (1976) pp. 350–359 " Casopis. Pešt. Mat. , 101 (1976) pp. 350–359 |
| [3] | J. Foran, P.D. Humke, "Some set-theoretic properties of 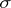 -porous sets" Real Anal. Exch. , 6 : 1 (1980/81) pp. 114–119 -porous sets" Real Anal. Exch. , 6 : 1 (1980/81) pp. 114–119 |
| [4] | J. Tkadlec, "Constructions of some non-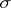 - -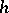 -porous sets on the real line" Real Anal. Exch. , 9 : 2 (1983/84) pp. 473–482 -porous sets on the real line" Real Anal. Exch. , 9 : 2 (1983/84) pp. 473–482 |
| [5] | S.J. Agronsky, A.M. Bruckner, "Local compactness and porosity in metric spaces" Real Anal. Exch. , 11 : 2 (1985/86) pp. 365–379 |
| [6] | Yu.A. Shevchenko, "On Vitali's covering theorem" Vestnik Moskov. Univ. Ser. 1. Mat. Mech. : 3 (1989) pp. 11–14 (In Russian) |
Porosity point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Porosity_point&oldid=14614