Difference between revisions of "Existentially closed"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 7: | Line 7: | ||
A member <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014033.png" /> of a class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014034.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014035.png" />-structures is called existentially closed (or existentially complete) with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014036.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014037.png" /> is existentially closed in every member <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014038.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014039.png" />, provided that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014040.png" /> is a substructure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014041.png" />. | A member <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014033.png" /> of a class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014034.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014035.png" />-structures is called existentially closed (or existentially complete) with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014036.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014037.png" /> is existentially closed in every member <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014038.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014039.png" />, provided that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014040.png" /> is a substructure of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014041.png" />. | ||
| − | If a [[Field|field]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014042.png" /> is existentially closed in an extension field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014043.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014044.png" /> is (relatively) algebraically closed in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014045.png" /> (cf. [[Algebraically closed field|Algebraically closed field]]). Hence, a field that is existentially closed with respect to all fields must be algebraically closed, and a formally real field that is existentially closed with respect to all formally real fields must be a [[ | + | If a [[Field|field]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014042.png" /> is existentially closed in an extension field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014043.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014044.png" /> is (relatively) algebraically closed in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014045.png" /> (cf. [[Algebraically closed field|Algebraically closed field]]). Hence, a field that is existentially closed with respect to all fields must be algebraically closed, and a [[formally real field]] that is existentially closed with respect to all formally real fields must be a [[real closed field]]. Existentially closed fields or rings (with respect to suitable classes) give rise to a corresponding Nullstellensatz. This is a theorem describing the form of a polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014046.png" /> depending on finitely many other polynomials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014047.png" />, provided that there is an existentially closed member <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014048.png" /> of the class containing the coefficients of the polynomials and such that every common root of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014049.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014050.png" /> is also a root of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014051.png" />. For the class of fields, the corresponding theorem is Hilbert's Nullstellensatz (cf. [[Hilbert theorem|Hilbert theorem]]). There are corresponding theorems for formally real fields (see [[Real closed field|Real closed field]]), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014052.png" />-valued fields (see [[P-adically closed field|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e110/e110140/e11014053.png" />-adically closed field]]), differential fields, division rings, commutative rings, and commutative regular rings. The general model-theoretic framework was considered by V. Weispfenning in 1977. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Cherlin, "Model theoretic algebra" , ''Lecture Notes in Mathematics'' , '''521''' , Springer (1976)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Cherlin, "Model theoretic algebra" , ''Lecture Notes in Mathematics'' , '''521''' , Springer (1976)</TD></TR></table> | ||
Revision as of 19:56, 7 December 2014
existentially complete
Let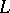 
be a first-order language (cf. Model (in logic)). A substructure 
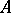of an 
-structure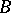 
(cf. Structure) is called existentially closed (or existentially complete) in 
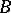if every existential sentence with parameters from 
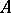is true in 
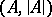if it is true in 
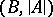. An existential sentence with parameters from 
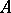is a closed formula 
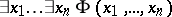, where 
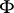is a formula without quantifiers in the first-order language of signature 
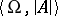, with 
the signature of 
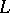(cf. Model theory).
If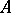 
is a substructure of 
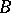and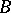 
admits an embedding, fixing the elements of 
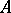, in some elementary extension of 
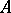(cf. Elementary theory), then 
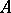is existentially closed in 
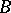. Conversely, if 
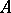is existentially closed in 
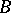and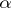 
is a cardinal number greater than the cardinality of 
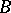, then 
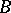admits an embedding, fixing the elements of 
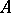, in every 
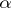-saturated extension of 
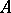(cf. also Model theory).
A member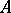 
of a class 
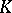of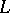 
-structures is called existentially closed (or existentially complete) with respect to 
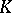if 
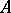is existentially closed in every member 
of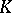 
, provided that 
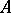is a substructure of 
.
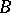If a field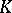 
is existentially closed in an extension field 
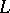, then 
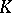is (relatively) algebraically closed in 
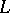(cf. Algebraically closed field). Hence, a field that is existentially closed with respect to all fields must be algebraically closed, and a formally real field that is existentially closed with respect to all formally real fields must be a real closed field. Existentially closed fields or rings (with respect to suitable classes) give rise to a corresponding Nullstellensatz. This is a theorem describing the form of a polynomial 
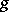depending on finitely many other polynomials 
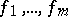, provided that there is an existentially closed member 
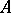of the class containing the coefficients of the polynomials and such that every common root of the 
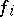in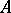 
is also a root of 
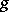. For the class of fields, the corresponding theorem is Hilbert's Nullstellensatz (cf. Hilbert theorem). There are corresponding theorems for formally real fields (see Real closed field), 
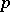-valued fields (see 
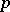-adically closed field), differential fields, division rings, commutative rings, and commutative regular rings. The general model-theoretic framework was considered by V. Weispfenning in 1977.
References
| [a1] | G. Cherlin, "Model theoretic algebra" , Lecture Notes in Mathematics , 521 , Springer (1976) |
How to Cite This Entry:
Existentially closed. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Existentially_closed&oldid=14384
Existentially closed. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Existentially_closed&oldid=14384
This article was adapted from an original article by F.-V. Kuhlmann (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article