Difference between revisions of "Inverse hyperbolic functions"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | i0523701.png | ||
| + | $#A+1 = 24 n = 0 | ||
| + | $#C+1 = 24 : ~/encyclopedia/old_files/data/I052/I.0502370 Inverse hyperbolic functions | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Functions inverse to the [[Hyperbolic functions|hyperbolic functions]]. The inverse hyperbolic functions are the inverse hyperbolic sine, cosine and tangent: $ \sinh ^ {-} 1 x $, | |
| + | $ \cosh ^ {-} 1 x $, | ||
| + | $ \mathop{\rm tanh} ^ {-} 1 x $; | ||
| + | other notations are: $ { \mathop{\rm arg} \sinh } x $, | ||
| + | $ { \mathop{\rm arg} \cosh } x $, | ||
| + | $ { \mathop{\rm arg} \mathop{\rm tanh} } x $. | ||
| − | + | The inverse hyperbolic functions of a real variable $ x $ | |
| + | are defined by the formulas | ||
| − | + | $$ | |
| + | \sinh ^ {-} 1 x = \ | ||
| + | \mathop{\rm ln} ( x + \sqrt {x ^ {2} + 1 } ) ,\ \ | ||
| + | - \infty < x < + \infty , | ||
| + | $$ | ||
| − | The inverse hyperbolic functions are single-valued and continuous at each point of their domain of definition, except for | + | $$ |
| + | \cosh ^ {-} 1 x = \ | ||
| + | \pm \mathop{\rm ln} ( x + \sqrt {x ^ {2} - 1 } ) ,\ \ | ||
| + | x \geq 1 , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \mathop{\rm tanh} ^ {-} 1 x = | ||
| + | \frac{1}{2} | ||
| + | \mathop{\rm ln} | ||
| + | \frac{1 | ||
| + | + x }{1 - x } | ||
| + | ,\ | x | < 1 . | ||
| + | $$ | ||
| + | |||
| + | The inverse hyperbolic functions are single-valued and continuous at each point of their domain of definition, except for $ \cosh ^ {-} 1 x $, | ||
| + | which is two-valued. In studying the properties of the inverse hyperbolic functions, one of the continuous branches of $ \cosh ^ {-} 1 x $ | ||
| + | is chosen, that is, in the formula above only one sign is taken (usually plus). For the graphs of these functions see the figure. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/i052370a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/i052370a.gif" /> | ||
| Line 17: | Line 52: | ||
There a number of relations between the inverse hyperbolic functions. For example, | There a number of relations between the inverse hyperbolic functions. For example, | ||
| − | + | $$ | |
| + | \sinh ^ {-} 1 x = \ | ||
| + | \mathop{\rm tanh} ^ {-} 1 \ | ||
| + | |||
| + | \frac{x}{\sqrt {x ^ {2} + 1 } } | ||
| + | ,\ \ | ||
| + | \mathop{\rm tanh} ^ {-} 1 x = \ | ||
| + | \sinh ^ {-} 1 \ | ||
| + | |||
| + | \frac{x}{\sqrt {1 - x ^ {2} } } | ||
| + | . | ||
| + | $$ | ||
The derivatives of the inverse hyperbolic functions are given by the formulas | The derivatives of the inverse hyperbolic functions are given by the formulas | ||
| − | + | $$ | |
| + | ( \sinh ^ {-} 1 x ) ^ \prime = \ | ||
| − | + | \frac{1}{\sqrt {x ^ {2} + 1 } } | |
| + | ,\ \ | ||
| + | ( \cosh ^ {-} 1 x ) ^ \prime = \pm | ||
| − | + | \frac{1}{\sqrt {x ^ {2} - 1 } } | |
| + | , | ||
| + | $$ | ||
| − | + | $$ | |
| + | ( \mathop{\rm tanh} ^ {-} 1 x ) ^ \prime = | ||
| + | \frac{1}{ {1 - x ^ {2} } } | ||
| + | . | ||
| + | $$ | ||
| − | + | The inverse hyperbolic functions of a complex variable $ z $ | |
| + | are defined by the same formulas as those for a real variable $ x $, | ||
| + | where $ \mathop{\rm ln} z $ | ||
| + | is understood to be the many-valued logarithmic function. The inverse hyperbolic functions of a complex variable are the analytic continuations to the complex plane of the corresponding functions of a real variable. | ||
| − | + | The inverse hyperbolic functions can be expressed in terms of the [[Inverse trigonometric functions|inverse trigonometric functions]] by the formulas | |
| − | + | $$ | |
| + | \sinh ^ {-} 1 z = - i { \mathop{\rm arc} \sin } i z , | ||
| + | $$ | ||
| + | $$ | ||
| + | \cosh ^ {-} 1 z = i { \mathop{\rm arc} \cos } z , | ||
| + | $$ | ||
| + | $$ | ||
| + | \mathop{\rm tanh} ^ {-} 1 z = - i { \mathop{\rm arc} \mathop{\rm tan} } i z . | ||
| + | $$ | ||
====Comments==== | ====Comments==== | ||
| − | The notations | + | The notations $ { \mathop{\rm arc} \sinh } x $, |
| + | $ { \mathop{\rm arc} \cosh } x $ | ||
| + | and $ { \mathop{\rm arc} \mathop{\rm tanh} } x $ | ||
| + | are also quite common. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M.R. Spiegel, "Complex variables" , ''Schaum's Outline Series'' , McGraw-Hill (1974)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M.R. Spiegel, "Complex variables" , ''Schaum's Outline Series'' , McGraw-Hill (1974)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972)</TD></TR></table> | ||
Revision as of 22:13, 5 June 2020
Functions inverse to the hyperbolic functions. The inverse hyperbolic functions are the inverse hyperbolic sine, cosine and tangent: $ \sinh ^ {-} 1 x $,
$ \cosh ^ {-} 1 x $,
$ \mathop{\rm tanh} ^ {-} 1 x $;
other notations are: $ { \mathop{\rm arg} \sinh } x $,
$ { \mathop{\rm arg} \cosh } x $,
$ { \mathop{\rm arg} \mathop{\rm tanh} } x $.
The inverse hyperbolic functions of a real variable $ x $ are defined by the formulas
$$ \sinh ^ {-} 1 x = \ \mathop{\rm ln} ( x + \sqrt {x ^ {2} + 1 } ) ,\ \ - \infty < x < + \infty , $$
$$ \cosh ^ {-} 1 x = \ \pm \mathop{\rm ln} ( x + \sqrt {x ^ {2} - 1 } ) ,\ \ x \geq 1 , $$
$$ \mathop{\rm tanh} ^ {-} 1 x = \frac{1}{2} \mathop{\rm ln} \frac{1 + x }{1 - x } ,\ | x | < 1 . $$
The inverse hyperbolic functions are single-valued and continuous at each point of their domain of definition, except for $ \cosh ^ {-} 1 x $, which is two-valued. In studying the properties of the inverse hyperbolic functions, one of the continuous branches of $ \cosh ^ {-} 1 x $ is chosen, that is, in the formula above only one sign is taken (usually plus). For the graphs of these functions see the figure.
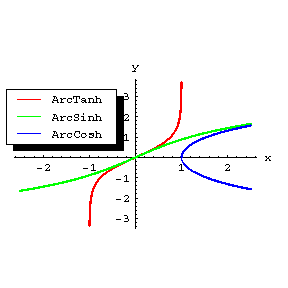
Figure: i052370a
There a number of relations between the inverse hyperbolic functions. For example,
$$ \sinh ^ {-} 1 x = \ \mathop{\rm tanh} ^ {-} 1 \ \frac{x}{\sqrt {x ^ {2} + 1 } } ,\ \ \mathop{\rm tanh} ^ {-} 1 x = \ \sinh ^ {-} 1 \ \frac{x}{\sqrt {1 - x ^ {2} } } . $$
The derivatives of the inverse hyperbolic functions are given by the formulas
$$ ( \sinh ^ {-} 1 x ) ^ \prime = \ \frac{1}{\sqrt {x ^ {2} + 1 } } ,\ \ ( \cosh ^ {-} 1 x ) ^ \prime = \pm \frac{1}{\sqrt {x ^ {2} - 1 } } , $$
$$ ( \mathop{\rm tanh} ^ {-} 1 x ) ^ \prime = \frac{1}{ {1 - x ^ {2} } } . $$
The inverse hyperbolic functions of a complex variable $ z $ are defined by the same formulas as those for a real variable $ x $, where $ \mathop{\rm ln} z $ is understood to be the many-valued logarithmic function. The inverse hyperbolic functions of a complex variable are the analytic continuations to the complex plane of the corresponding functions of a real variable.
The inverse hyperbolic functions can be expressed in terms of the inverse trigonometric functions by the formulas
$$ \sinh ^ {-} 1 z = - i { \mathop{\rm arc} \sin } i z , $$
$$ \cosh ^ {-} 1 z = i { \mathop{\rm arc} \cos } z , $$
$$ \mathop{\rm tanh} ^ {-} 1 z = - i { \mathop{\rm arc} \mathop{\rm tan} } i z . $$
Comments
The notations $ { \mathop{\rm arc} \sinh } x $, $ { \mathop{\rm arc} \cosh } x $ and $ { \mathop{\rm arc} \mathop{\rm tanh} } x $ are also quite common.
References
| [a1] | M.R. Spiegel, "Complex variables" , Schaum's Outline Series , McGraw-Hill (1974) |
| [a2] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) |
Inverse hyperbolic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_hyperbolic_functions&oldid=12740