Difference between revisions of "Routes to chaos"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | r0827501.png | ||
| + | $#A+1 = 138 n = 4 | ||
| + | $#C+1 = 138 : ~/encyclopedia/old_files/data/R082/R.0802750 Routes to chaos | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
This phrase refers to the process by which a simple attracting set for a [[Dynamical system|dynamical system]] (like a fixed point or periodic orbit) becomes chaotic as an external parameter is varied. | This phrase refers to the process by which a simple attracting set for a [[Dynamical system|dynamical system]] (like a fixed point or periodic orbit) becomes chaotic as an external parameter is varied. | ||
One considers a one-parameter family of differential equations | One considers a one-parameter family of differential equations | ||
| − | + | $$ \tag{a1 } | |
| + | |||
| + | \frac{d }{dt } | ||
| + | x( t) = F _ \lambda ( x( t)),\ x( 0) = x _ {0} , | ||
| + | $$ | ||
or difference equations (mappings) | or difference equations (mappings) | ||
| − | + | $$ \tag{a2 } | |
| + | x _ {n+ 1 } = F _ \lambda ( x _ {n} ) , | ||
| + | $$ | ||
| − | where | + | where $ F $ |
| + | is a smooth function of the real parameter $ \lambda $ | ||
| + | and the point $ x $, | ||
| + | which belongs to some finite-dimensional phase space (like $ \mathbf R ^ {n} $); | ||
| + | $ x _ {0} $ | ||
| + | is an initial condition. (Other domains are sometimes of interest, for example, mappings of the circle $ S ^ {1} $ | ||
| + | or the torus $ T ^ {2} $.) | ||
| + | Suppose that for a fixed value of $ \lambda $, | ||
| + | the initial conditions in some open set in the phase space approach a compact set $ A $ | ||
| + | which exhibits sensitive dependence on initial conditions. (Such a set $ A $ | ||
| + | is also called an attractor. However, there is no universally satisfactory definition of attractor (see e.g. [[#References|[a1]]]). In this article it means an [[Invariant set|invariant set]] for the mapping or flow that attracts almost-all initial conditions in some open neighbourhood, that cannot be split into disjoint non-trivial closed invariant subsets, and on which the motion is recurrent. See [[#References|[a2]]] for a discussion of sensitive dependence in one-dimensional mappings; cf. also [[Repelling set|Repelling set]]; [[Strange attractor|Strange attractor]].) Roughly speaking, if $ x _ {0} $ | ||
| + | and $ y _ {0} $ | ||
| + | are two nearby initial conditions on $ A $, | ||
| + | their trajectories remain close only for a short time. Then the trajectories separate at an exponential rate until their subsequent motion appears uncorrelated. (The rate of separation eventually saturates since $ A $ | ||
| + | is bounded.) The attractor $ A $ | ||
| + | is chaotic whenever $ A $ | ||
| + | exhibits sensitive dependence on initial conditions (cf. also [[Chaos|Chaos]]). This article discusses four ways in which chaotic attractors for (a1) and (a2) can arise as the parameter $ \lambda $ | ||
| + | is varied. These are the most common known routes to chaos, and there is ample confirmation of their existence in physical experiments. Other routes to chaos have been found (see e.g. [[#References|[a3]]]), and more undoubtedly remain undiscovered, particularly in high-dimensional systems. See [[#References|[a4]]] for a review article and bibliography. | ||
==Period doubling route to chaos.== | ==Period doubling route to chaos.== | ||
| − | In this route to chaos, a fixed point loses stability (in a pitchfork bifurcation, cf. [[Bifurcation|Bifurcation]]) to an attracting period-2 orbit as the parameter passes some critical value. At some later parameter value, the period-2 orbit loses stability (in a pitchfork bifurcation) to a period-4 orbit, etc. The parameter values at which these period doublings occur form an increasing sequence converging to some finite value | + | In this route to chaos, a fixed point loses stability (in a pitchfork bifurcation, cf. [[Bifurcation|Bifurcation]]) to an attracting period-2 orbit as the parameter passes some critical value. At some later parameter value, the period-2 orbit loses stability (in a pitchfork bifurcation) to a period-4 orbit, etc. The parameter values at which these period doublings occur form an increasing sequence converging to some finite value $ \lambda _ \infty $, |
| + | at which the original fixed point is replaced by an aperiodic attractor (which may be chaotic for $ \lambda > \lambda _ \infty $). | ||
M.J. Feigenbaum | M.J. Feigenbaum | ||
| Line 18: | Line 54: | ||
originally studied period doubling in the difference equation | originally studied period doubling in the difference equation | ||
| − | + | $$ \tag{a3 } | |
| + | x _ {n+ 1 } = F _ \lambda ( x _ {n} ) = \lambda x _ {n} ( 1 - x _ {n} ), | ||
| + | $$ | ||
| − | also called the quadratic mapping. When | + | also called the quadratic mapping. When $ \lambda > 1 $, |
| + | $ F _ \lambda $ | ||
| + | has a non-zero fixed point at $ x _ {f} = 1 - 1/ \lambda $ | ||
| + | which is stable for $ 1 < \lambda < 3 $, | ||
| + | since | ||
| − | + | $$ | |
| + | \left | | ||
| + | \frac{dF _ \lambda }{dx } | ||
| + | ( x _ {f} ) \right | = | 2- \lambda | < 1. | ||
| + | $$ | ||
| − | When | + | When $ \lambda = \lambda _ {1} = 3 $, |
| + | the derivative at $ x _ {f} $ | ||
| + | is $ - 1 $. | ||
| + | For slightly larger values of $ \lambda $, | ||
| + | the derivative is larger than $ 1 $ | ||
| + | in absolute value, and $ x _ {f} $ | ||
| + | is unstable: almost-all initial conditions in $ [ 0, 1] $ | ||
| + | are attracted to a period-2 orbit, $ x _ {1} = F _ \lambda ( x _ {2} ) $, | ||
| + | $ x _ {2} = F _ \lambda ( x _ {1} ) $. | ||
| + | A similar derivative evaluation for $ F _ \lambda ^ { 2 } ( x _ {i} ) = F _ \lambda ( F _ \lambda ( x _ {i} )) = x _ {i} $, | ||
| + | $ i= 1,2 $, | ||
| + | shows that each $ x _ {i} $ | ||
| + | is stable for $ \lambda _ {1} < \lambda < \lambda _ {2} \approx 3.449 $. | ||
| + | At $ \lambda _ {2} $ | ||
| + | each $ x _ {i} $ | ||
| + | loses its stability because the derivative $ dF _ {\lambda _ {2} } ^ { 2 } ( x _ {i} )/dx = - 1 $. | ||
| + | As before, each $ x _ {i} $ | ||
| + | is replaced by a pair of attracting points $ x _ {i1 } $, | ||
| + | $ x _ {i2 } $ | ||
| + | such that $ x _ {i1 } = F _ \lambda ^ { 2 } ( x _ {i2 } ) $, | ||
| + | $ x _ {i2 } = F _ \lambda ^ { 2 } ( x _ {i1 } ) $, | ||
| + | $ i= 1, 2 $. | ||
| + | The points $ x _ {ij } $ | ||
| + | correspond to an attracting period-4 orbit for $ F _ \lambda $ | ||
| + | when $ \lambda $ | ||
| + | is slightly larger than $ \lambda _ {2} $. | ||
| + | This process continues indefinitely; at each bifurcation, the periodic orbit is replaced by a new attracting periodic orbit of twice the period. The parameter values at which the bifurcations occur form an increasing sequence $ \{ \lambda _ {k} \} $ | ||
| + | that is bounded above by a number $ \lambda _ \infty \approx 3.5699 $ | ||
| + | with the property that | ||
| − | + | $$ \tag{a4 } | |
| + | \lim\limits _ {k \rightarrow \infty } | ||
| + | \frac{\lambda _ {k} - \lambda _ {k- 1 } }{\lambda _ {k+ 1 } - \lambda _ {k} } | ||
| + | = \delta \approx 4.6692. | ||
| + | $$ | ||
| − | The number | + | The number $ \delta $ |
| + | is the Feigenbaum constant. It is a remarkable fact that $ \delta $ | ||
| + | is independent of the details of the mapping $ F _ \lambda $ | ||
| + | as long as $ F _ \lambda $ | ||
| + | satisfies certain general hypotheses; see , [[#References|[a6]]] for details. Chaos occurs in the quadratic mapping for many values of $ \lambda < 4 $. | ||
| + | In fact, M. Jakobson [[#References|[a7]]] proved that the set of such parameter values has positive measure. | ||
| − | Similar results hold in higher dimensions, i.e., for mappings | + | Similar results hold in higher dimensions, i.e., for mappings $ \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ |
| + | where $ n > 1 $[[#References|[a8]]]. In [[#References|[a9]]] it is shown how period-doubling cascades arise in the formation of "horseshoes" as the parameter varies. [[#References|[a10]]] contains a collection of papers describing the existence of period doubling in a variety of physical situations. | ||
==Intermittency route to chaos.== | ==Intermittency route to chaos.== | ||
| − | Y. Pomeau and P. Manneville [[#References|[a11]]] describe how an attracting periodic orbit (like a fixed point) for < | + | Y. Pomeau and P. Manneville [[#References|[a11]]] describe how an attracting periodic orbit (like a fixed point) for $ \lambda < \lambda _ {c} $ |
| + | can disappear and be replaced by a chaotic attractor for $ \lambda > \lambda _ {c} $. | ||
| + | For $ \lambda $ | ||
| + | slightly larger than $ \lambda _ {c} $, | ||
| + | initial conditions near the periodic orbit remain there for a long time. This regular behaviour is interrupted by a "burst" in which the trajectory moves away from a neighbourhood of the periodic orbit and exhibits possibly irregular behaviour. Eventually, the trajectory re-enters the region near the periodic orbit and the process is repeated. The dynamical behaviour for $ \lambda > \lambda _ {c} $ | ||
| + | is characterized by an infinite sequence of intervals of nearly periodic (laminar) motion followed by bursts. The length of the laminar regions scales as $ ( \lambda - \lambda _ {c} ) ^ {- 1/2 } $ | ||
| + | for $ \lambda $ | ||
| + | near $ \lambda _ {c} $[[#References|[a11]]]. | ||
| − | Three types of intermittency are distinguished, depending on the eigenvalues of the associated [[Jacobian|Jacobian]] matrix of partial derivatives evaluated at the periodic orbit. Type- | + | Three types of intermittency are distinguished, depending on the eigenvalues of the associated [[Jacobian|Jacobian]] matrix of partial derivatives evaluated at the periodic orbit. Type- $ 1 $ |
| + | intermittency occurs when a stable and an unstable periodic orbit that coexist for $ \lambda < \lambda _ {c} $ | ||
| + | collide at $ \lambda = \lambda _ {c} $( | ||
| + | the Jacobian matrix at the resulting periodic orbit has eigenvalue $ 1 $) | ||
| + | and disappear for $ \lambda > \lambda _ {c} $( | ||
| + | i.e., there is a saddle-node bifurcation at $ \lambda _ {c} $). | ||
| + | An example using the difference equation | ||
| − | + | $$ \tag{a5 } | |
| + | x _ {n+ 1 } = F _ \lambda ( x _ {n} ) = 1 - \lambda x _ {n} ^ {2} | ||
| + | $$ | ||
| − | is given in [[#References|[a4]]]. For | + | is given in [[#References|[a4]]]. For $ \lambda > 1.75 $, |
| + | $ F _ \lambda ^ { 3 } $ | ||
| + | has one stable and one unstable period-3 orbit. They collide at $ \lambda = 1.75 $, | ||
| + | and for $ \lambda $ | ||
| + | slightly less than $ 1.75 $, | ||
| + | the iterates exhibit a nearly period-3 motion interrupted by bursts. Type- $ 1 $ | ||
| + | intermittency has been found in Poincaré mappings of the Lorenz equations (cf. [[Lorenz attractor|Lorenz attractor]], [[#References|[a11]]]) and in experiments on oscillating chemical reactions [[#References|[a12]]]. | ||
| − | Type- | + | Type- $ 2 $ |
| + | intermittency occurs when the eigenvalues of the associated Jacobian matrix are complex and cross the unit circle away from the real line. In type- $ 3 $ | ||
| + | intermittency, the eigenvalues pass through $ - 1 $. | ||
| + | Heuristic arguments and numerical evidence suggest that the [[Lyapunov characteristic exponent|Lyapunov characteristic exponent]] of the chaotic attractor created when $ \lambda $ | ||
| + | passes $ \lambda _ {c} $ | ||
| + | scales as $ ( \lambda - \lambda _ {c} ) ^ {- 1/2 } $, | ||
| + | at least in the case of type- $ 1 $ | ||
| + | and type- $ 3 $ | ||
| + | intermittency [[#References|[a11]]]. | ||
==Ruelle–Takens–Newhouse route to chaos.== | ==Ruelle–Takens–Newhouse route to chaos.== | ||
| − | Suppose that for < | + | Suppose that for $ \lambda < \lambda _ {1} $ |
| + | there is an attracting fixed point for (a1) that loses its stability in a Hopf bifurcation at $ \lambda = \lambda _ {1} $( | ||
| + | i.e., the fixed point is replaced by an attracting periodic orbit). In addition, suppose that at $ \lambda = \lambda _ {2} > \lambda _ {1} $ | ||
| + | there is another Hopf bifurcation to a quasi-periodic orbit (i.e., the attractor is now a torus $ T ^ {2} $). | ||
| + | A subsequent Hopf bifurcation at $ \lambda = \lambda _ {3} > \lambda _ {2} $ | ||
| + | creates a quasi-periodic $ 3 $- | ||
| + | torus. However, S.E. Newhouse, D. Ruelle and F. Takens [[#References|[a13]]] showed that for $ n \geq 3 $ | ||
| + | every constant vector field on the torus $ T ^ {n} $ | ||
| + | can be perturbed by an arbitrarily small amount to a new vector field with a chaotic attractor. Thus, in an experiment, one may see a bifurcation from a $ 2 $- | ||
| + | frequency quasi-periodic flow to a chaotic attractor; see, for example, [[#References|[a14]]], . This route to turbulence is in contrast to the classical theory of L. Landau and E. Lifshitz [[#References|[a16]]], which says that turbulence arises from the successive addition of incommensurate frequences as a parameter is increased. | ||
==Crisis route to chaos.== | ==Crisis route to chaos.== | ||
| − | The previous examples showed how an existing attractor can change its character as a parameter is varied. In a crisis, there is initially only a chaotic transient for | + | The previous examples showed how an existing attractor can change its character as a parameter is varied. In a crisis, there is initially only a chaotic transient for $ \lambda > \lambda _ {c} $, |
| + | i.e., initial conditions in some region of the phase space approach what appears to be a chaotic attractor and may spend a long time near it. Eventually, however, the orbit leaves for another part of the phase space, never to return. The time spent near the chaotic transient becomes longer as $ \lambda \rightarrow \lambda _ {c} $. | ||
| + | When $ \lambda \leq \lambda _ {c} $, | ||
| + | the chaotic transient becomes a chaotic attractor: initial conditions that once escaped now remain forever. | ||
| − | A simple example of a crisis is given by the quadratic mapping (a3). For | + | A simple example of a crisis is given by the quadratic mapping (a3). For $ \lambda > 4 $, |
| + | almost every initial condition in the interval $ I=[ 0, 1] $ | ||
| + | generates a trajectory that bounces chaotically in $ I $ | ||
| + | for a time. Eventually, some iterate falls to the left of $ 0 $, | ||
| + | and the orbit tends to $ - \infty $. | ||
| + | At $ \lambda = 4 $, | ||
| + | the transient is converted to an attractor: almost every initial condition in $ I $ | ||
| + | approaches a chaotic attractor. | ||
| − | In this example, the chaotic attractor is contained in | + | In this example, the chaotic attractor is contained in $ ( 0, 1) $ |
| + | when $ \lambda < 4 $. | ||
| + | The crisis occurs at $ \lambda = 4 $ | ||
| + | when an interior point of $ ( 0, 1) $ | ||
| + | is mapped to $ 1 $, | ||
| + | which is part of the stable manifold of the unstable fixed point at $ 0 $. | ||
| + | For $ \lambda > 4 $, | ||
| + | a portion of the interval $ I $ | ||
| + | is mapped into the basin of attraction (cf. [[Chaos|Chaos]]) for $ - \infty $, | ||
| + | so the chaotic attractor is replaced by a chaotic transient. The mean time that typical initial conditions spend in $ I $ | ||
| + | before escaping to $ - \infty $ | ||
| + | scales as $ ( \lambda - 4) ^ {- 1/2 } $ | ||
| + | with the parameter [[#References|[a17]]]. | ||
Similar results hold in higher dimensions. [[#References|[a17]]] discusses the Hénon mapping | Similar results hold in higher dimensions. [[#References|[a17]]] discusses the Hénon mapping | ||
| − | + | $$ | |
| + | x _ {n+ 1 } = 1 - \lambda x _ {n} ^ {2} + y _ {n} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | y _ {n+ 1 } = 0.3 x _ {n} , | ||
| + | $$ | ||
| − | where a | + | where a $ 6 $- |
| + | piece and a $ 4 $- | ||
| + | piece chaotic attractor coexist for $ 1.0624 < \lambda < \lambda _ {c} \approx 1.08074 $. | ||
| + | As $ \lambda \rightarrow \lambda _ {c} $, | ||
| + | the $ 6 $- | ||
| + | piece attractor approaches the stable manifold of a period-6 saddle orbit that forms part of the boundary of the basin of attraction for the $ 4 $- | ||
| + | piece attractor. When $ \lambda > \lambda _ {c} $, | ||
| + | part of the $ 6 $- | ||
| + | piece attractor crosses this stable manifold. Thus, for $ \lambda > \lambda _ {c} $ | ||
| + | the $ 6 $- | ||
| + | piece attractor becomes a transient — eventually some iterate maps into the basin of the $ 4 $- | ||
| + | piece attractor. Numerical evidence suggests that the mean time spent near the chaotic transient is proportional to $ ( \lambda - \lambda _ {c} ) ^ {- \gamma } $, | ||
| + | where $ \gamma $ | ||
| + | is a "critical exponent" that can be expressed in terms of the eigenvalues associated with the periodic orbit involved in the crisis [[#References|[a18]]]. The existence of crises has also been demonstrated for the Lorenz equations and mappings of the torus [[#References|[a17]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Milnor, "On the concept of attractor" ''Commun. Math. Phys.'' , '''99''' (1985) pp. 177–195</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Guckenheimer, "Sensitive dependence to initial conditions for one-dimensional maps" ''Commun. Math. Phys.'' , '''70''' (1979) pp. 133–160</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E.N. Lorenz, ''Physica D'' , '''35''' (1989) pp. 299–317</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.-P. Eckmann, "Roads to turbulence in dissipative dynamical systems" ''Rev. Mod. Phys.'' , '''53''' (1981) pp. 643–654</TD></TR><TR><TD valign="top">[a5a]</TD> <TD valign="top"> M.J. Feigenbaum, "Qualitative universality for a class of nonlinear transformations" ''J. Stat. Phys.'' , '''19''' (1978) pp. 25–52</TD></TR><TR><TD valign="top">[a5b]</TD> <TD valign="top"> M.J. Feigenbaum, "The universal metric properties of nonlinear transformations" ''J. Stat. Phys.'' , '''21''' (1979) pp. 669–706</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Collet, J.-P. Eckmann, O.E. Lanford, "Universal properties of maps on an interval" ''Commun. Math. Phys.'' , '''76''' (1980) pp. 211–254</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Jakobson, "Absolutely continuous invariant measures for one-parameter families of one-dimensional maps" ''Commun. Math. Phys.'' , '''81''' (1981) pp. 39–88</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> P. Collet, J.-P. Eckmann, H. Koch, "Period doubling bifurcations for families of maps on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750142.png" />" ''J. Stat. Phys.'' , '''25''' (1981) pp. 1–14</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> J.A. Yorke, K.T. Alligood, "Period doubling cascades of attractors: a prerequisite for horseshoes" ''Commun. Math. Phys.'' , '''101''' (1985) pp. 305–321</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> P. Cvitanović (ed.) , ''Universality in chaos'' , A. Hilger (1989)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> Y. Pomeau, P. Manneville, "Intermittent transition to turbulence in dissipative dynamical systems" ''Commun. Math. Phys.'' , '''74''' (1980) pp. 189–197</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> F. Argoul, A. Arneodo, P. Richetti, J.C. Roux, H.L. Swinney, ''Acct. Chem. Res.'' , '''20''' (1987) pp. 436–442</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S.E. Newhouse, D. Ruelle, F. Takens, "Occurrence of strange axiom <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750143.png" /> attractors near quasiperiodic flow on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750144.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750145.png" />" ''Commun. Math. Phys.'' , '''64''' (1978) pp. 35–40</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> M. Giglio, S. Musazzi, U. Perini, "Transition to chaotic behaviour via a reproducible sequence of period-doubling bifurcations" ''Phys. Rev. Lett.'' , '''47''' (1981) pp. 243–246</TD></TR><TR><TD valign="top">[a15a]</TD> <TD valign="top"> P.R. Fenstermacher, H.L. Swinney, J.P. Gollub, "Dynamical instabilities and transition to chaotic Taylor vortex flow" ''J. Fluid Mech.'' , '''94''' (1979) pp. 103–128</TD></TR><TR><TD valign="top">[a15b]</TD> <TD valign="top"> A. Brandstäter, H.L. Swinney, ''Phys. Rev. A'' , '''35''' (1987) pp. 2207–2220</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian)</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> C. Grebogi, E. Ott, J.A. Yorke, "Crises, sudden changes in chaotic attractors, and transient chaos" ''Physica D'' , '''7''' (1983) pp. 181–200</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> C. Grebogi, E. Ott, J.A. Yorke, ''Phys. Rev. Lett.'' , '''57''' (1986) pp. 1284–1287</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Milnor, "On the concept of attractor" ''Commun. Math. Phys.'' , '''99''' (1985) pp. 177–195</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Guckenheimer, "Sensitive dependence to initial conditions for one-dimensional maps" ''Commun. Math. Phys.'' , '''70''' (1979) pp. 133–160</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E.N. Lorenz, ''Physica D'' , '''35''' (1989) pp. 299–317</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.-P. Eckmann, "Roads to turbulence in dissipative dynamical systems" ''Rev. Mod. Phys.'' , '''53''' (1981) pp. 643–654</TD></TR><TR><TD valign="top">[a5a]</TD> <TD valign="top"> M.J. Feigenbaum, "Qualitative universality for a class of nonlinear transformations" ''J. Stat. Phys.'' , '''19''' (1978) pp. 25–52</TD></TR><TR><TD valign="top">[a5b]</TD> <TD valign="top"> M.J. Feigenbaum, "The universal metric properties of nonlinear transformations" ''J. Stat. Phys.'' , '''21''' (1979) pp. 669–706</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Collet, J.-P. Eckmann, O.E. Lanford, "Universal properties of maps on an interval" ''Commun. Math. Phys.'' , '''76''' (1980) pp. 211–254</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M. Jakobson, "Absolutely continuous invariant measures for one-parameter families of one-dimensional maps" ''Commun. Math. Phys.'' , '''81''' (1981) pp. 39–88</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> P. Collet, J.-P. Eckmann, H. Koch, "Period doubling bifurcations for families of maps on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750142.png" />" ''J. Stat. Phys.'' , '''25''' (1981) pp. 1–14</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> J.A. Yorke, K.T. Alligood, "Period doubling cascades of attractors: a prerequisite for horseshoes" ''Commun. Math. Phys.'' , '''101''' (1985) pp. 305–321</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> P. Cvitanović (ed.) , ''Universality in chaos'' , A. Hilger (1989)</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> Y. Pomeau, P. Manneville, "Intermittent transition to turbulence in dissipative dynamical systems" ''Commun. Math. Phys.'' , '''74''' (1980) pp. 189–197</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> F. Argoul, A. Arneodo, P. Richetti, J.C. Roux, H.L. Swinney, ''Acct. Chem. Res.'' , '''20''' (1987) pp. 436–442</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S.E. Newhouse, D. Ruelle, F. Takens, "Occurrence of strange axiom <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750143.png" /> attractors near quasiperiodic flow on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750144.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r082/r082750/r082750145.png" />" ''Commun. Math. Phys.'' , '''64''' (1978) pp. 35–40</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> M. Giglio, S. Musazzi, U. Perini, "Transition to chaotic behaviour via a reproducible sequence of period-doubling bifurcations" ''Phys. Rev. Lett.'' , '''47''' (1981) pp. 243–246</TD></TR><TR><TD valign="top">[a15a]</TD> <TD valign="top"> P.R. Fenstermacher, H.L. Swinney, J.P. Gollub, "Dynamical instabilities and transition to chaotic Taylor vortex flow" ''J. Fluid Mech.'' , '''94''' (1979) pp. 103–128</TD></TR><TR><TD valign="top">[a15b]</TD> <TD valign="top"> A. Brandstäter, H.L. Swinney, ''Phys. Rev. A'' , '''35''' (1987) pp. 2207–2220</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian)</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> C. Grebogi, E. Ott, J.A. Yorke, "Crises, sudden changes in chaotic attractors, and transient chaos" ''Physica D'' , '''7''' (1983) pp. 181–200</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> C. Grebogi, E. Ott, J.A. Yorke, ''Phys. Rev. Lett.'' , '''57''' (1986) pp. 1284–1287</TD></TR></table> | ||
Latest revision as of 08:12, 6 June 2020
This phrase refers to the process by which a simple attracting set for a dynamical system (like a fixed point or periodic orbit) becomes chaotic as an external parameter is varied.
One considers a one-parameter family of differential equations
$$ \tag{a1 } \frac{d }{dt } x( t) = F _ \lambda ( x( t)),\ x( 0) = x _ {0} , $$
or difference equations (mappings)
$$ \tag{a2 } x _ {n+ 1 } = F _ \lambda ( x _ {n} ) , $$
where $ F $ is a smooth function of the real parameter $ \lambda $ and the point $ x $, which belongs to some finite-dimensional phase space (like $ \mathbf R ^ {n} $); $ x _ {0} $ is an initial condition. (Other domains are sometimes of interest, for example, mappings of the circle $ S ^ {1} $ or the torus $ T ^ {2} $.) Suppose that for a fixed value of $ \lambda $, the initial conditions in some open set in the phase space approach a compact set $ A $ which exhibits sensitive dependence on initial conditions. (Such a set $ A $ is also called an attractor. However, there is no universally satisfactory definition of attractor (see e.g. [a1]). In this article it means an invariant set for the mapping or flow that attracts almost-all initial conditions in some open neighbourhood, that cannot be split into disjoint non-trivial closed invariant subsets, and on which the motion is recurrent. See [a2] for a discussion of sensitive dependence in one-dimensional mappings; cf. also Repelling set; Strange attractor.) Roughly speaking, if $ x _ {0} $ and $ y _ {0} $ are two nearby initial conditions on $ A $, their trajectories remain close only for a short time. Then the trajectories separate at an exponential rate until their subsequent motion appears uncorrelated. (The rate of separation eventually saturates since $ A $ is bounded.) The attractor $ A $ is chaotic whenever $ A $ exhibits sensitive dependence on initial conditions (cf. also Chaos). This article discusses four ways in which chaotic attractors for (a1) and (a2) can arise as the parameter $ \lambda $ is varied. These are the most common known routes to chaos, and there is ample confirmation of their existence in physical experiments. Other routes to chaos have been found (see e.g. [a3]), and more undoubtedly remain undiscovered, particularly in high-dimensional systems. See [a4] for a review article and bibliography.
Period doubling route to chaos.
In this route to chaos, a fixed point loses stability (in a pitchfork bifurcation, cf. Bifurcation) to an attracting period-2 orbit as the parameter passes some critical value. At some later parameter value, the period-2 orbit loses stability (in a pitchfork bifurcation) to a period-4 orbit, etc. The parameter values at which these period doublings occur form an increasing sequence converging to some finite value $ \lambda _ \infty $, at which the original fixed point is replaced by an aperiodic attractor (which may be chaotic for $ \lambda > \lambda _ \infty $).
M.J. Feigenbaum
originally studied period doubling in the difference equation
$$ \tag{a3 } x _ {n+ 1 } = F _ \lambda ( x _ {n} ) = \lambda x _ {n} ( 1 - x _ {n} ), $$
also called the quadratic mapping. When $ \lambda > 1 $, $ F _ \lambda $ has a non-zero fixed point at $ x _ {f} = 1 - 1/ \lambda $ which is stable for $ 1 < \lambda < 3 $, since
$$ \left | \frac{dF _ \lambda }{dx } ( x _ {f} ) \right | = | 2- \lambda | < 1. $$
When $ \lambda = \lambda _ {1} = 3 $, the derivative at $ x _ {f} $ is $ - 1 $. For slightly larger values of $ \lambda $, the derivative is larger than $ 1 $ in absolute value, and $ x _ {f} $ is unstable: almost-all initial conditions in $ [ 0, 1] $ are attracted to a period-2 orbit, $ x _ {1} = F _ \lambda ( x _ {2} ) $, $ x _ {2} = F _ \lambda ( x _ {1} ) $. A similar derivative evaluation for $ F _ \lambda ^ { 2 } ( x _ {i} ) = F _ \lambda ( F _ \lambda ( x _ {i} )) = x _ {i} $, $ i= 1,2 $, shows that each $ x _ {i} $ is stable for $ \lambda _ {1} < \lambda < \lambda _ {2} \approx 3.449 $. At $ \lambda _ {2} $ each $ x _ {i} $ loses its stability because the derivative $ dF _ {\lambda _ {2} } ^ { 2 } ( x _ {i} )/dx = - 1 $. As before, each $ x _ {i} $ is replaced by a pair of attracting points $ x _ {i1 } $, $ x _ {i2 } $ such that $ x _ {i1 } = F _ \lambda ^ { 2 } ( x _ {i2 } ) $, $ x _ {i2 } = F _ \lambda ^ { 2 } ( x _ {i1 } ) $, $ i= 1, 2 $. The points $ x _ {ij } $ correspond to an attracting period-4 orbit for $ F _ \lambda $ when $ \lambda $ is slightly larger than $ \lambda _ {2} $. This process continues indefinitely; at each bifurcation, the periodic orbit is replaced by a new attracting periodic orbit of twice the period. The parameter values at which the bifurcations occur form an increasing sequence $ \{ \lambda _ {k} \} $ that is bounded above by a number $ \lambda _ \infty \approx 3.5699 $ with the property that
$$ \tag{a4 } \lim\limits _ {k \rightarrow \infty } \frac{\lambda _ {k} - \lambda _ {k- 1 } }{\lambda _ {k+ 1 } - \lambda _ {k} } = \delta \approx 4.6692. $$
The number $ \delta $ is the Feigenbaum constant. It is a remarkable fact that $ \delta $ is independent of the details of the mapping $ F _ \lambda $ as long as $ F _ \lambda $ satisfies certain general hypotheses; see , [a6] for details. Chaos occurs in the quadratic mapping for many values of $ \lambda < 4 $. In fact, M. Jakobson [a7] proved that the set of such parameter values has positive measure.
Similar results hold in higher dimensions, i.e., for mappings $ \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ where $ n > 1 $[a8]. In [a9] it is shown how period-doubling cascades arise in the formation of "horseshoes" as the parameter varies. [a10] contains a collection of papers describing the existence of period doubling in a variety of physical situations.
Intermittency route to chaos.
Y. Pomeau and P. Manneville [a11] describe how an attracting periodic orbit (like a fixed point) for $ \lambda < \lambda _ {c} $ can disappear and be replaced by a chaotic attractor for $ \lambda > \lambda _ {c} $. For $ \lambda $ slightly larger than $ \lambda _ {c} $, initial conditions near the periodic orbit remain there for a long time. This regular behaviour is interrupted by a "burst" in which the trajectory moves away from a neighbourhood of the periodic orbit and exhibits possibly irregular behaviour. Eventually, the trajectory re-enters the region near the periodic orbit and the process is repeated. The dynamical behaviour for $ \lambda > \lambda _ {c} $ is characterized by an infinite sequence of intervals of nearly periodic (laminar) motion followed by bursts. The length of the laminar regions scales as $ ( \lambda - \lambda _ {c} ) ^ {- 1/2 } $ for $ \lambda $ near $ \lambda _ {c} $[a11].
Three types of intermittency are distinguished, depending on the eigenvalues of the associated Jacobian matrix of partial derivatives evaluated at the periodic orbit. Type- $ 1 $ intermittency occurs when a stable and an unstable periodic orbit that coexist for $ \lambda < \lambda _ {c} $ collide at $ \lambda = \lambda _ {c} $( the Jacobian matrix at the resulting periodic orbit has eigenvalue $ 1 $) and disappear for $ \lambda > \lambda _ {c} $( i.e., there is a saddle-node bifurcation at $ \lambda _ {c} $). An example using the difference equation
$$ \tag{a5 } x _ {n+ 1 } = F _ \lambda ( x _ {n} ) = 1 - \lambda x _ {n} ^ {2} $$
is given in [a4]. For $ \lambda > 1.75 $, $ F _ \lambda ^ { 3 } $ has one stable and one unstable period-3 orbit. They collide at $ \lambda = 1.75 $, and for $ \lambda $ slightly less than $ 1.75 $, the iterates exhibit a nearly period-3 motion interrupted by bursts. Type- $ 1 $ intermittency has been found in Poincaré mappings of the Lorenz equations (cf. Lorenz attractor, [a11]) and in experiments on oscillating chemical reactions [a12].
Type- $ 2 $ intermittency occurs when the eigenvalues of the associated Jacobian matrix are complex and cross the unit circle away from the real line. In type- $ 3 $ intermittency, the eigenvalues pass through $ - 1 $. Heuristic arguments and numerical evidence suggest that the Lyapunov characteristic exponent of the chaotic attractor created when $ \lambda $ passes $ \lambda _ {c} $ scales as $ ( \lambda - \lambda _ {c} ) ^ {- 1/2 } $, at least in the case of type- $ 1 $ and type- $ 3 $ intermittency [a11].
Ruelle–Takens–Newhouse route to chaos.
Suppose that for $ \lambda < \lambda _ {1} $ there is an attracting fixed point for (a1) that loses its stability in a Hopf bifurcation at $ \lambda = \lambda _ {1} $( i.e., the fixed point is replaced by an attracting periodic orbit). In addition, suppose that at $ \lambda = \lambda _ {2} > \lambda _ {1} $ there is another Hopf bifurcation to a quasi-periodic orbit (i.e., the attractor is now a torus $ T ^ {2} $). A subsequent Hopf bifurcation at $ \lambda = \lambda _ {3} > \lambda _ {2} $ creates a quasi-periodic $ 3 $- torus. However, S.E. Newhouse, D. Ruelle and F. Takens [a13] showed that for $ n \geq 3 $ every constant vector field on the torus $ T ^ {n} $ can be perturbed by an arbitrarily small amount to a new vector field with a chaotic attractor. Thus, in an experiment, one may see a bifurcation from a $ 2 $- frequency quasi-periodic flow to a chaotic attractor; see, for example, [a14], . This route to turbulence is in contrast to the classical theory of L. Landau and E. Lifshitz [a16], which says that turbulence arises from the successive addition of incommensurate frequences as a parameter is increased.
Crisis route to chaos.
The previous examples showed how an existing attractor can change its character as a parameter is varied. In a crisis, there is initially only a chaotic transient for $ \lambda > \lambda _ {c} $, i.e., initial conditions in some region of the phase space approach what appears to be a chaotic attractor and may spend a long time near it. Eventually, however, the orbit leaves for another part of the phase space, never to return. The time spent near the chaotic transient becomes longer as $ \lambda \rightarrow \lambda _ {c} $. When $ \lambda \leq \lambda _ {c} $, the chaotic transient becomes a chaotic attractor: initial conditions that once escaped now remain forever.
A simple example of a crisis is given by the quadratic mapping (a3). For $ \lambda > 4 $, almost every initial condition in the interval $ I=[ 0, 1] $ generates a trajectory that bounces chaotically in $ I $ for a time. Eventually, some iterate falls to the left of $ 0 $, and the orbit tends to $ - \infty $. At $ \lambda = 4 $, the transient is converted to an attractor: almost every initial condition in $ I $ approaches a chaotic attractor.
In this example, the chaotic attractor is contained in $ ( 0, 1) $ when $ \lambda < 4 $. The crisis occurs at $ \lambda = 4 $ when an interior point of $ ( 0, 1) $ is mapped to $ 1 $, which is part of the stable manifold of the unstable fixed point at $ 0 $. For $ \lambda > 4 $, a portion of the interval $ I $ is mapped into the basin of attraction (cf. Chaos) for $ - \infty $, so the chaotic attractor is replaced by a chaotic transient. The mean time that typical initial conditions spend in $ I $ before escaping to $ - \infty $ scales as $ ( \lambda - 4) ^ {- 1/2 } $ with the parameter [a17].
Similar results hold in higher dimensions. [a17] discusses the Hénon mapping
$$ x _ {n+ 1 } = 1 - \lambda x _ {n} ^ {2} + y _ {n} , $$
$$ y _ {n+ 1 } = 0.3 x _ {n} , $$
where a $ 6 $- piece and a $ 4 $- piece chaotic attractor coexist for $ 1.0624 < \lambda < \lambda _ {c} \approx 1.08074 $. As $ \lambda \rightarrow \lambda _ {c} $, the $ 6 $- piece attractor approaches the stable manifold of a period-6 saddle orbit that forms part of the boundary of the basin of attraction for the $ 4 $- piece attractor. When $ \lambda > \lambda _ {c} $, part of the $ 6 $- piece attractor crosses this stable manifold. Thus, for $ \lambda > \lambda _ {c} $ the $ 6 $- piece attractor becomes a transient — eventually some iterate maps into the basin of the $ 4 $- piece attractor. Numerical evidence suggests that the mean time spent near the chaotic transient is proportional to $ ( \lambda - \lambda _ {c} ) ^ {- \gamma } $, where $ \gamma $ is a "critical exponent" that can be expressed in terms of the eigenvalues associated with the periodic orbit involved in the crisis [a18]. The existence of crises has also been demonstrated for the Lorenz equations and mappings of the torus [a17].
References
| [a1] | J. Milnor, "On the concept of attractor" Commun. Math. Phys. , 99 (1985) pp. 177–195 |
| [a2] | J. Guckenheimer, "Sensitive dependence to initial conditions for one-dimensional maps" Commun. Math. Phys. , 70 (1979) pp. 133–160 |
| [a3] | E.N. Lorenz, Physica D , 35 (1989) pp. 299–317 |
| [a4] | J.-P. Eckmann, "Roads to turbulence in dissipative dynamical systems" Rev. Mod. Phys. , 53 (1981) pp. 643–654 |
| [a5a] | M.J. Feigenbaum, "Qualitative universality for a class of nonlinear transformations" J. Stat. Phys. , 19 (1978) pp. 25–52 |
| [a5b] | M.J. Feigenbaum, "The universal metric properties of nonlinear transformations" J. Stat. Phys. , 21 (1979) pp. 669–706 |
| [a6] | P. Collet, J.-P. Eckmann, O.E. Lanford, "Universal properties of maps on an interval" Commun. Math. Phys. , 76 (1980) pp. 211–254 |
| [a7] | M. Jakobson, "Absolutely continuous invariant measures for one-parameter families of one-dimensional maps" Commun. Math. Phys. , 81 (1981) pp. 39–88 |
| [a8] | P. Collet, J.-P. Eckmann, H. Koch, "Period doubling bifurcations for families of maps on 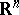 " J. Stat. Phys. , 25 (1981) pp. 1–14 " J. Stat. Phys. , 25 (1981) pp. 1–14 |
| [a9] | J.A. Yorke, K.T. Alligood, "Period doubling cascades of attractors: a prerequisite for horseshoes" Commun. Math. Phys. , 101 (1985) pp. 305–321 |
| [a10] | P. Cvitanović (ed.) , Universality in chaos , A. Hilger (1989) |
| [a11] | Y. Pomeau, P. Manneville, "Intermittent transition to turbulence in dissipative dynamical systems" Commun. Math. Phys. , 74 (1980) pp. 189–197 |
| [a12] | F. Argoul, A. Arneodo, P. Richetti, J.C. Roux, H.L. Swinney, Acct. Chem. Res. , 20 (1987) pp. 436–442 |
| [a13] | S.E. Newhouse, D. Ruelle, F. Takens, "Occurrence of strange axiom 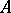 attractors near quasiperiodic flow on attractors near quasiperiodic flow on 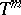 , , 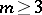 " Commun. Math. Phys. , 64 (1978) pp. 35–40 " Commun. Math. Phys. , 64 (1978) pp. 35–40 |
| [a14] | M. Giglio, S. Musazzi, U. Perini, "Transition to chaotic behaviour via a reproducible sequence of period-doubling bifurcations" Phys. Rev. Lett. , 47 (1981) pp. 243–246 |
| [a15a] | P.R. Fenstermacher, H.L. Swinney, J.P. Gollub, "Dynamical instabilities and transition to chaotic Taylor vortex flow" J. Fluid Mech. , 94 (1979) pp. 103–128 |
| [a15b] | A. Brandstäter, H.L. Swinney, Phys. Rev. A , 35 (1987) pp. 2207–2220 |
| [a16] | L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian) |
| [a17] | C. Grebogi, E. Ott, J.A. Yorke, "Crises, sudden changes in chaotic attractors, and transient chaos" Physica D , 7 (1983) pp. 181–200 |
| [a18] | C. Grebogi, E. Ott, J.A. Yorke, Phys. Rev. Lett. , 57 (1986) pp. 1284–1287 |
Routes to chaos. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Routes_to_chaos&oldid=12583