Difference between revisions of "User:Ulf Rehmann/Table of automatically generated TeX code"
Ulf Rehmann (talk | contribs) m |
Ulf Rehmann (talk | contribs) m (Ulf Rehmann moved page User:Ulf Rehmann/Table to User:Ulf Rehmann/Table of automatically generated TeX code) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | This page gives an analysis of [[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|the code here]], [[User:Maximilian Janisch/latexlist|generated automatically from some png files underlying our old wiki pages]]. | ||
| + | As this page does contain a lot of $\TeX$ code, it loads slowly. | ||
| + | |||
| + | Under the name of some of our EoM-pages the table below lists some png files, displaying their image and their $TeX$ rendering (automatically retrieved and corrected by hand). | ||
| + | The first column gives the running number in this table, followed (in parentheses) by the number used [[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E| here]]. | ||
| + | The last column gives the confidence and the name of the png file, followed (in parentheses) by the number it has in the sequence of all png files called by its calling EoM-page. | ||
| + | |||
| + | Here is a short survey of the more systematic errors which seem to occur: | ||
| + | |||
| + | ; 1. Trailing punctuation is dismissed. | ||
| + | :[concerns almost all images] ; technically: pixels in sparse last pixel columns of bit images are suppressed/ignored? | ||
| + | |||
| + | ; 2. "Displayed" images are not recognized as such. | ||
| + | :[concerns almost all images] | ||
| + | :Therefore these are displayed too small, and like "inline" $\TeX$ format. | ||
| + | : | ||
| + | :Remark: This cannot be discovered from the png file, it has to be retrieved from the html markup in the calling file: Displayed images are embedded in some html <table> markup. | ||
| + | : | ||
| + | ;3. Sparse initial column pixels of the bit image are dismissed | ||
| + | :(in parts this affects essential symbols), [see nr. 15,16,36,43,58,59,60,61,62,63,97,109] | ||
| + | |||
| + | ;4. Some fonts are not recognized: | ||
| + | :\cal: [7.12.25.26,30,31,32,33,95,111] \mathbf: [30,83,111,127] \bf:[ 133,148,149] | ||
| + | : | ||
| + | ;5. Semi-colon is interpreted as double pipe = "||" :[33,49,86,101] | ||
| + | : | ||
| + | ;6. Some code is not displayed at all. | ||
| + | : (This seems to be a bug of our MathJax TeX interpreter.) [67,74,78,81,83,94,101,106] | ||
| + | : This seems to happen when a string "\text {" is involved, can apparently be fixed by using "\text{", but still unclear. | ||
| + | : | ||
| + | ;7. Questions: | ||
| + | : The different interpretation of the matrix delimiters in [56-63] is a bit surprising. Should be checked! | ||
| + | : Also, the vanishing of some '-' signs in the first column of some matrices, maybe that is related to 3.? | ||
| + | |||
==[[Algebraic curve]]== | ==[[Algebraic curve]]== | ||
{| class="wikitable" style="text-align: left; width: 1740px;" | {| class="wikitable" style="text-align: left; width: 1740px;" | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 1.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|23.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011450/a01145065.png || $g \leq \left\{ \begin{array} { l l } { \frac { ( n - 2 ) ^ { 2 } } { 4 } } & { \text { for even } n } \\ { \frac { ( n - 1 ) ( n - 3 ) } { 4 } } & { \text { for odd } n } \end{array} \right.$ || | + | | 1.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|23.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011450/a01145065.png | ||
| + | || $g \leq \left\{ \begin{array} { l l } { \frac { ( n - 2 ) ^ { 2 } } { 4 } } & { \text { for even } n } \\ { \frac { ( n - 1 ) ( n - 3 ) } { 4 } } & { \text { for odd } n } \end{array} \right.$ | ||
| + | ||$$g\leq \left\{ | ||
| + | \begin {array}{ll} | ||
| + | {\frac {(n-2)^2}4} &{\text{ for even }n,}\\ | ||
| + | {\frac {(n-1)(n-3)}4} &{\text{ for odd }n,} | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.698 | ||
a01145065.png (65) | a01145065.png (65) | ||
| Line 17: | Line 60: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 2.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|116.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150014.png || $\theta = \int _ { 0 } ^ { \lambda } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ || | + | | 2.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|116.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150014.png | ||
| + | || $\theta = \int _ { 0 } ^ { \lambda } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | ||
| + | ||$$\theta =\int\limits _ 0^{\lambda }\frac {dx}{\sqrt {(1-c^2x^2)(1-e^2x^2)}},$$ | ||
| + | || conf 0.997 | ||
a01150014.png (14) | a01150014.png (14) | ||
|- | |- | ||
| − | | 3.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|133.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150021.png || $\omega = 2 \int _ { 0 } ^ { 1 / c } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ || | + | | 3.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|133.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150021.png | ||
| + | || $\omega = 2 \int _ { 0 } ^ { 1 / c } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | ||
| + | ||$$\omega =2\int\limits _ 0^{1/c}\frac {dx}{\sqrt {(1-c^2x^2)(1-e^2x^2)}},$$ | ||
| + | || conf 0.973 | ||
a01150021.png (21) | a01150021.png (21) | ||
|- | |- | ||
| − | | 4.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|67.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150022.png || $\overline { w } = 2 \int _ { 0 } ^ { 1 / \varepsilon } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ || $$\widetilde | + | | 4.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|67.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150022.png | ||
| + | || $\overline { w } = 2 \int _ { 0 } ^ { 1 / \varepsilon } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | ||
| + | ||$$\widetilde w=2\int\limits _ 0^{1/\varepsilon }\frac {dx}{\sqrt {(1-c^2x^2)(1-e^2x^2)}},$$ | ||
| + | || conf 0.107 | ||
a01150022.png (22) | a01150022.png (22) | ||
|- | |- | ||
| − | | 5.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|105.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150044.png || $\theta ( v + \pi i r ) = \theta ( r ) , \quad \theta ( v + \alpha _ { j } ) = e ^ { L _ { j } ( v ) } \theta ( v )$ || | + | | 5.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|105.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150044.png | ||
| + | || $\theta ( v + \pi i r ) = \theta ( r ) , \quad \theta ( v + \alpha _ { j } ) = e ^ { L _ { j } ( v ) } \theta ( v )$ | ||
| + | ||$$\theta (v+\pi i r )=\theta (r),\quad \theta (v+\alpha _ j)=e^{L_j(v)}\theta (v),$$ | ||
| + | || conf 0.775 | ||
a01150044.png (44) | a01150044.png (44) | ||
|- | |- | ||
| − | | 6.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|17.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150078.png || $\left( \begin{array} { l l } { \alpha } & { b } \\ { c } & { d } \end{array} \right) \equiv \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) ( \operatorname { mod } 7 )$ || | + | | 6.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|17.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011500/a01150078.png | ||
| + | || $\left( \begin{array} { l l } { \alpha } & { b } \\ { c } & { d } \end{array} \right) \equiv \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) ( \operatorname { mod } 7 )$ | ||
| + | ||$$\left( | ||
| + | \begin {array}{ll} | ||
| + | {\alpha } &b\\ | ||
| + | c &d | ||
| + | \end {array} | ||
| + | \right)\equiv \left( | ||
| + | \begin {array}{ll} | ||
| + | 1&0\\ | ||
| + | 0&1 | ||
| + | \end {array} | ||
| + | \right)(\operatorname {mod}7).$$ | ||
| + | || conf 0.440 | ||
a01150078.png (78) | a01150078.png (78) | ||
| Line 48: | Line 121: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 7.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|144.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a011640132.png || $0 \rightarrow O _ { V } \rightarrow E _ { \alpha } \rightarrow T _ { V } \rightarrow 0$ || $$0 \rightarrow {\cal O} | + | | 7.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|144.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a011640132.png | ||
| + | || $0 \rightarrow O _ { V } \rightarrow E _ { \alpha } \rightarrow T _ { V } \rightarrow 0$ | ||
| + | ||$$0\rightarrow {\cal O}_V\rightarrow E _ {\alpha }\rightarrow T _ V\rightarrow 0$$ | ||
| + | || conf 0.981 | ||
a011640132.png (132) | a011640132.png (132) | ||
|- | |- | ||
| − | | 8.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|73.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a011640137.png || $M = \operatorname { dim } \operatorname { Im } ( H ^ { 1 } ( V , E _ { \alpha } ) \rightarrow H ^ { 1 } ( V , T _ { V } ) )$ || $$ M = \operatorname { dim } \operatorname { Im } ( H ^ | + | | 8.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|73.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a011640137.png | ||
| + | || $M = \operatorname { dim } \operatorname { Im } ( H ^ { 1 } ( V , E _ { \alpha } ) \rightarrow H ^ { 1 } ( V , T _ { V } ) )$ | ||
| + | ||$$M=\operatorname {dim}\operatorname {Im}(H^1(V,E_{\alpha })\rightarrow H ^1(V,T_V)).$$ | ||
| + | || conf 0.997 | ||
a011640137.png (137) | a011640137.png (137) | ||
|- | |- | ||
| − | | 9.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|88.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a011640139.png || $\operatorname { dim } _ { k } H ^ { 2 } ( V , E _ { \alpha } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , T _ { V } )$ || $$ \operatorname { dim } | + | | 9.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|88.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a011640139.png | ||
| + | || $\operatorname { dim } _ { k } H ^ { 2 } ( V , E _ { \alpha } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , T _ { V } )$ | ||
| + | ||$$\operatorname {dim}_kH^2(V,E_{\alpha })+\operatorname {dim}_kH^2(V,T_V).$$ | ||
| + | || conf 0.996 | ||
a011640139.png (139) | a011640139.png (139) | ||
|- | |- | ||
| − | | 10.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|117.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164027.png || $N _ { m } = \left( \begin{array} { c } { m + 3 } \\ { 3 } \end{array} \right) - d m + 2 t + \tau + p - 1$ || $$ | + | | 10.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|117.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164027.png | ||
| + | || $N _ { m } = \left( \begin{array} { c } { m + 3 } \\ { 3 } \end{array} \right) - d m + 2 t + \tau + p - 1$ | ||
| + | ||$$N_m=\left(\begin {array}c{m+3}\\ | ||
| + | 3 | ||
| + | \end {array} | ||
| + | \right)-dm+2t+\tau +p-1.$$ | ||
| + | || conf 0.369 | ||
a01164027.png (27) | a01164027.png (27) | ||
|- | |- | ||
| − | | 11.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|72.]]) || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164029.png || $p _ { \alpha } ( V ) = \left( \begin{array} { c } { n - 1 } \\ { 3 } \end{array} \right) - d ( n - 1 ) + 2 t + \tau + p - 1$ || $$ | + | | 11.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|72.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164029.png | ||
| + | || $p _ { \alpha } ( V ) = \left( \begin{array} { c } { n - 1 } \\ { 3 } \end{array} \right) - d ( n - 1 ) + 2 t + \tau + p - 1$ | ||
| + | ||$$p_{\alpha }(V)=\left(\begin {array}c{n-1}\\ | ||
| + | 3 | ||
| + | \end {array} | ||
| + | \right)-d(n-1)+2t+\tau +p-1$$ | ||
| + | || conf 0.396 | ||
a01164029.png (29) | a01164029.png (29) | ||
|- | |- | ||
| − | | 12.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|68.]])*|| https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164047.png || $p _ { x } ( V ) = - \operatorname { dim } _ { k } H _ { 1 } ( V , O _ { V } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , O _ { V } ) =$ || | + | | 12.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|68.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164047.png | ||
| + | || $p _ { x } ( V ) = - \operatorname { dim } _ { k } H _ { 1 } ( V , O _ { V } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , O _ { V } ) =$ | ||
| + | ||$$p_{\alpha }(V)=-\operatorname {dim}_kH_1(V,{\cal O}_V)+\operatorname {dim}_kH^2(V,{\cal O}_V)=$$ | ||
| + | || conf 0.756 F | ||
a01164047.png (47) | a01164047.png (47) | ||
|- | |- | ||
| − | | 13.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|93.]])*|| https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164053.png || $1 + p _ { x } ( V ) = \frac { \operatorname { deg } ( c _ { 1 } ^ { 2 } ) + \operatorname { deg } ( c _ { 2 } ) } { 12 }$ || | + | | 13.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|93.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/a/a011/a011640/a01164053.png | ||
| + | || $1 + p _ { x } ( V ) = \frac { \operatorname { deg } ( c _ { 1 } ^ { 2 } ) + \operatorname { deg } ( c _ { 2 } ) } { 12 }$ | ||
| + | ||$$1+p_{\alpha }(V)=\frac {\operatorname {deg}(c_1^2)+\operatorname {deg}(c_2)}{12},$$ | ||
| + | || conf 0.752 F | ||
a01164053.png (53) | a01164053.png (53) | ||
| Line 87: | Line 194: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 14.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|33.]])*|| https://www.encyclopediaofmath.org/legacyimages/c/c020/c020550/c0205509.png || $\mathfrak { g } 0 = \{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists \mathfrak { n } X , H \in Z ( ( \text { ad } H ) ^ { n } X , H ( X ) = 0 ) \}$ || | + | | 14.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|33.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/c/c020/c020550/c0205509.png | ||
| + | || $\mathfrak { g } 0 = \{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists \mathfrak { n } X , H \in Z ( ( \text { ad } H ) ^ { n } X , H ( X ) = 0 ) \}$ | ||
| + | ||$$\mathfrak g_0=\big\{X\in \mathfrak g:\forall H \in \mathfrak t\exists n_{X,H}\in {\mathbb Z}((\text{ ad }H)^{n_{X,H}}(X)=0)\big\},$$ | ||
| + | || conf 0.110 F | ||
c0205509.png (9) | c0205509.png (9) | ||
| Line 102: | Line 213: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 15.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|49.]])*|| https://www.encyclopediaofmath.org/legacyimages/c/c020/c020570/c0205704.png || $f _ { j } ] = \delta _ { i j } h _ { i } , \quad [ h _ { i } , e _ { j } ] = \alpha _ { i j } e _ { j } , \quad [ h _ { i } , f _ { j } ] = - \alpha _ { j } f _ { j }$ || $$ [e_i, | + | | 15.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|49.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/c/c020/c020570/c0205704.png | ||
| + | || $f _ { j } ] = \delta _ { i j } h _ { i } , \quad [ h _ { i } , e _ { j } ] = \alpha _ { i j } e _ { j } , \quad [ h _ { i } , f _ { j } ] = - \alpha _ { j } f _ { j }$ | ||
| + | ||$$[e_i,f_j]=\delta _ {ij}h_i,\quad [h_i,e_j]=\alpha _ {ij}e_j,\quad [h_i,f_j]=-\alpha _ {ij}f_j,$$ | ||
| + | || conf 0.149 F | ||
c0205704.png (4) | c0205704.png (4) | ||
|- | |- | ||
| − | | 16.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|55.]])*|| https://www.encyclopediaofmath.org/legacyimages/c/c020/c020570/c02057064.png || $\rightarrow H ^ { p } ( X , S ) \rightarrow H ^ { p } ( X , F ) \stackrel { \phi p } { \rightarrow } H ^ { p } ( X , G ) \rightarrow$ || $$ \dots \rightarrow H ^ | + | | 16.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|55.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/c/c020/c020570/c02057064.png | ||
| + | || $\rightarrow H ^ { p } ( X , S ) \rightarrow H ^ { p } ( X , F ) \stackrel { \phi p } { \rightarrow } H ^ { p } ( X , G ) \rightarrow$ | ||
| + | ||$$\dots \rightarrow H ^p(X,S)\rightarrow H ^p(X,F)\stackrel {\phi_p }{\rightarrow }H^p(X,G)\rightarrow $$ | ||
| + | || conf 0.853 F | ||
c02057064.png (64) | c02057064.png (64) | ||
| Line 121: | Line 240: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 17.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|7.]]) || https://www.encyclopediaofmath.org/legacyimages/c/c023/c023330/c02333033.png || $H = \frac { 1 } { 36 } \left| \begin{array} { c c } { \frac { \partial ^ { 2 } f } { \partial x ^ { 2 } } } & { \frac { \partial ^ { 2 } f } { \partial x \partial y } } \\ { \frac { \partial ^ { 2 } f } { \partial x \partial y } } & { \frac { \partial ^ { 2 } f } { \partial y ^ { 2 } } } \end{array} \right| =$ || $$H = \frac | + | | 17.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|7.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/c/c023/c023330/c02333033.png | ||
| + | || $H = \frac { 1 } { 36 } \left| \begin{array} { c c } { \frac { \partial ^ { 2 } f } { \partial x ^ { 2 } } } & { \frac { \partial ^ { 2 } f } { \partial x \partial y } } \\ { \frac { \partial ^ { 2 } f } { \partial x \partial y } } & { \frac { \partial ^ { 2 } f } { \partial y ^ { 2 } } } \end{array} \right| =$ | ||
| + | ||$$H=\frac 1{36}\left| | ||
| + | \begin {array}{cc} | ||
| + | {\frac {\partial ^2f}{\partial x ^2}} &{\frac {\partial ^2f}{\partial x \partial y }}\\ | ||
| + | {\frac {\partial ^2f}{\partial x \partial y }} &{\frac {\partial ^2f}{\partial y ^2}} | ||
| + | \end {array} | ||
| + | \right|=$$ | ||
| + | || conf 0.956 | ||
c02333033.png (33) | c02333033.png (33) | ||
|- | |- | ||
| − | | 18.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|76.]]) || https://www.encyclopediaofmath.org/legacyimages/c/c023/c023330/c02333034.png || $= ( a _ { 0 } a _ { 2 } - a _ { 1 } ^ { 2 } ) x ^ { 2 } + ( a _ { 0 } a _ { 3 } - a _ { 1 } a _ { 2 } ) x y + ( a _ { 1 } a _ { 3 } - a _ { 2 } ^ { 2 } ) y ^ { 2 }$ || $$ = ( | + | | 18.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|76.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/c/c023/c023330/c02333034.png | ||
| + | || $= ( a _ { 0 } a _ { 2 } - a _ { 1 } ^ { 2 } ) x ^ { 2 } + ( a _ { 0 } a _ { 3 } - a _ { 1 } a _ { 2 } ) x y + ( a _ { 1 } a _ { 3 } - a _ { 2 } ^ { 2 } ) y ^ { 2 }$ | ||
| + | ||$$=(a_0a_2-a_1^2)x^2+(a_0a_3-a_1a_2)xy+(a_1a_3-a_2^2)y^2$$ | ||
| + | || conf 0.549 | ||
c02333034.png (34) | c02333034.png (34) | ||
|- | |- | ||
| − | | 19.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|11.]])*|| https://www.encyclopediaofmath.org/legacyimages/c/c023/c023330/c02333035.png || $( \alpha _ { 0 } , \alpha _ { 1 } , \alpha _ { 2 } , \alpha _ { 3 } ) \mapsto ( \alpha _ { 0 } \alpha _ { 2 } - \alpha _ { 1 } ^ { 2 } , \frac { 1 } { 2 } ( \alpha _ { 0 } \alpha _ { 3 } - \alpha _ { 1 } \alpha _ { 2 } ) , \alpha _ { 1 } \alpha _ { 3 } - \alpha _ { 2 } ^ { 2 } )$ || $$ ( \alpha _ | + | | 19.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|11.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/c/c023/c023330/c02333035.png | ||
| + | || $( \alpha _ { 0 } , \alpha _ { 1 } , \alpha _ { 2 } , \alpha _ { 3 } ) \mapsto ( \alpha _ { 0 } \alpha _ { 2 } - \alpha _ { 1 } ^ { 2 } , \frac { 1 } { 2 } ( \alpha _ { 0 } \alpha _ { 3 } - \alpha _ { 1 } \alpha _ { 2 } ) , \alpha _ { 1 } \alpha _ { 3 } - \alpha _ { 2 } ^ { 2 } )$ | ||
| + | ||$$(\alpha _ 0,\alpha _ 1,\alpha _ 2,\alpha _ 3)\mapsto (\alpha _ 0\alpha _ 2-\alpha _ 1^2,\frac 12(\alpha _ 0\alpha _ 3-\alpha _ 1\alpha _ 2),\alpha _ 1\alpha _ 3-\alpha _ 2^2)$$ | ||
| + | || conf 0.521 F | ||
c02333035.png (35) | c02333035.png (35) | ||
| Line 144: | Line 280: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 20.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|26.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700175.png || $\operatorname { Aut } _ { R ^ { \prime } } ( X ^ { \prime } | X _ { 0 } ) \rightarrow \operatorname { Aut } _ { R } ( X _ { R ^ { \prime } } ^ { \prime } \otimes R | X _ { 0 } )$ || | + | | 20.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|26.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700175.png | ||
| + | || $\operatorname { Aut } _ { R ^ { \prime } } ( X ^ { \prime } | X _ { 0 } ) \rightarrow \operatorname { Aut } _ { R } ( X _ { R ^ { \prime } } ^ { \prime } \otimes R | X _ { 0 } )$ | ||
| + | ||$$\operatorname {Aut}_{R^{\prime }}(X^{\prime }|X_0)\rightarrow \operatorname {Aut}_R(X_{R^{\prime }}^{\prime }\otimes R |X_0)$$ | ||
| + | || conf 0.683 | ||
\ | \ | ||
d030700175.png (175) | d030700175.png (175) | ||
|- | |- | ||
| − | | 21.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|27.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700190.png || $\operatorname { dim } _ { k } H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } ) - \operatorname { dim } M _ { X _ { 0 } } \leq \operatorname { dim } _ { k } H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } )$ || $$ \operatorname { dim } | + | | 21.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|27.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700190.png | ||
| + | || $\operatorname { dim } _ { k } H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } ) - \operatorname { dim } M _ { X _ { 0 } } \leq \operatorname { dim } _ { k } H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } )$ | ||
| + | ||$$\operatorname {dim}_kH^1(X_0,T_{X_0})-\operatorname {dim}M_{X_0}\leq \operatorname {dim}_kH^2(X_0,T_{X_0}).$$ | ||
| + | || conf 0.944 | ||
d030700190.png (190) | d030700190.png (190) | ||
|- | |- | ||
| − | | 22.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|78.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700263.png || $\alpha \circ b = \alpha b + \sum _ { i = 1 } ^ { \infty } \phi _ { i } ( \alpha , b ) t ^ { i } , \quad \alpha , b \in V$ || $$ \alpha \circ b = \alpha b + \sum _ { i = 1 } ^ { \infty } \phi _ | + | | 22.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|78.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700263.png | ||
| + | || $\alpha \circ b = \alpha b + \sum _ { i = 1 } ^ { \infty } \phi _ { i } ( \alpha , b ) t ^ { i } , \quad \alpha , b \in V$ | ||
| + | ||$$\alpha \circ b =\alpha b +\sum _ {i=1}^{\infty }\phi _ i(\alpha ,b)t^i,\quad \alpha ,b\in V,$$ | ||
| + | || conf 0.097 F | ||
d030700263.png (263) | d030700263.png (263) | ||
|- | |- | ||
| − | | 23.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|96.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700270.png || $\Phi ( \alpha ) = \alpha + \sum _ { i = 1 } ^ { \infty } t ^ { i } \phi _ { i } ( \alpha ) , \quad \alpha \in V$ || $$ \Phi ( \alpha ) = \alpha + \sum _ { i = 1 } ^ { \infty } t ^ | + | | 23.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|96.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d030/d030700/d030700270.png | ||
| + | || $\Phi ( \alpha ) = \alpha + \sum _ { i = 1 } ^ { \infty } t ^ { i } \phi _ { i } ( \alpha ) , \quad \alpha \in V$ | ||
| + | ||$$\Phi (\alpha )=\alpha +\sum _ {i=1}^{\infty }t^i\phi _ i(\alpha ),\quad \alpha \in V,$$ | ||
| + | || conf 0.873 F | ||
d030700270.png (270) | d030700270.png (270) | ||
| Line 171: | Line 323: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 24.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|106.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d031830107.png || $S ^ { t } F = \sum _ { j = 1 } ^ { r } c _ { j } A ^ { p _ { j } } A _ { 1 } ^ { i _ { 1 j } } \dots A _ { m - l } ^ { i _ { m - l } , j }$ || $$ S ^ | + | | 24.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|106.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d031830107.png | ||
| + | || $S ^ { t } F = \sum _ { j = 1 } ^ { r } c _ { j } A ^ { p _ { j } } A _ { 1 } ^ { i _ { 1 j } } \dots A _ { m - l } ^ { i _ { m - l } , j }$ | ||
| + | ||$$S^tF=\sum _ {j=1}^rc_jA^{p_j}A_1^{i_{1j}}\dots A _ {m-l}^{i_{{m-l},j}},$$ | ||
| + | || conf 0.149 | ||
d031830107.png (107) | d031830107.png (107) | ||
|- | |- | ||
| − | | 25.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|146.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d031830141.png || $( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$ || $ ( \eta _ | + | | 25.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|146.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d031830141.png | ||
| + | || $( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$ | ||
| + | ||$(\eta _ 1,\ldots ,\eta _ k)\rightarrow {}_{\cal F}(\zeta _ 1,\ldots ,\zeta _ k)$ | ||
| + | || conf 0.562 F | ||
d031830141.png (141) | d031830141.png (141) | ||
|- | |- | ||
| − | | 26.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|145.]])$^F$*|| https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d031830150.png || $( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$ || $ ( \eta _ | + | | 26.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|145.]])$^F$* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d031830150.png | ||
| + | || $( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$ | ||
| + | ||$(\eta _ 1,\ldots ,\eta _ n)\rightarrow {}_{\cal F}(\zeta _ 1,\ldots ,\zeta _ n)$ | ||
| + | || conf 0.376 F | ||
d031830150.png (150) | d031830150.png (150) | ||
|- | |- | ||
| − | | 27.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|57.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d03183016.png || $\omega _ { V } = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$ || $$ \omega _ | + | | 27.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|57.]]) |
| + | |||
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d03183016.png | ||
| + | |||
| + | || $\omega _ { V } = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$ | ||
| + | |||
| + | ||$$\omega _ V=\sum _ {0\leq i \leq m }\alpha _ i\left( | ||
| + | \begin {array}c{x+i}\\ | ||
| + | i | ||
| + | \end {array} | ||
| + | \right),$$ | ||
| + | || conf 0.780 | ||
d03183016.png (16) | d03183016.png (16) | ||
|- | |- | ||
| − | | 28.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|111.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d03183043.png || $e _ { i j } = \operatorname { ord } _ { Y } _ { j } F _ { i } , \quad 1 \leq i \leq n , \quad i \leq j \leq n$ || | + | | 28.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|111.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d031/d031830/d03183043.png | ||
| + | || $e _ { i j } = \operatorname { ord } _ { Y } _ { j } F _ { i } , \quad 1 \leq i \leq n , \quad i \leq j \leq n$ | ||
| + | ||$$e_{ij}=\operatorname {ord}_{Y_j}F_i,\quad 1 \leq i \leq n ,\quad i \leq j \leq n,$$ | ||
| + | || conf 0.187 | ||
d03183043.png (43) | d03183043.png (43) | ||
| Line 202: | Line 381: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 29.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|48.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d032/d032490/d03249029.png || $\omega _ { \eta / F } ( x ) = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$ || | + | | 29.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|48.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d032/d032490/d03249029.png | ||
| + | || $\omega _ { \eta / F } ( x ) = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$ | ||
| + | ||$$\omega _ {\eta /F}(x)=\sum _ {0\leq i \leq m }\alpha _ i\left(\begin {array}c{x+i}\\ | ||
| + | i | ||
| + | \end {array} | ||
| + | \right),$$ | ||
| + | || conf 0.968 | ||
d03249029.png (29) | d03249029.png (29) | ||
| Line 217: | Line 403: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 30.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|118.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120173.png || $H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow C$ || $$ H ^ | + | | 30.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|118.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120173.png | ||
| + | || $H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow C$ | ||
| + | ||$$H^p(X,{\cal F})\times H _ c^{n-p}(X,\operatorname {Hom}({\cal F},\Omega ))\rightarrow {\mathbf C},$$ | ||
| + | || conf 0.824 F | ||
d034120173.png (173) | d034120173.png (173) | ||
|- | |- | ||
| − | | 31.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|59.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120175.png || $H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow H _ { c } ^ { n } ( X , \Omega )$ || $$ H ^ | + | | 31.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|59.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120175.png | ||
| + | || $H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow H _ { c } ^ { n } ( X , \Omega )$ | ||
| + | ||$$H^p(X,{\cal F})\times H _ c^{n-p}(X,\operatorname {Hom}({\cal F},\Omega ))\rightarrow H _ c^n(X,\Omega )$$ | ||
| + | || conf 0.921 F | ||
d034120175.png (175) | d034120175.png (175) | ||
|- | |- | ||
| − | | 32.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|124.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120184.png || $( H ^ { p } ( X , F ) ) ^ { \prime } \cong H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) )$ || $$ ( H ^ | + | | 32.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|124.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120184.png | ||
| + | || $( H ^ { p } ( X , F ) ) ^ { \prime } \cong H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) )$ | ||
| + | ||$$(H^p(X,{\cal F}))^{\prime }\cong H _ c^{n-p}(X,\operatorname {Hom}({\cal F},\Omega )).$$ | ||
| + | || conf 0.829 F | ||
d034120184.png (184) | d034120184.png (184) | ||
|- | |- | ||
| − | | 33.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|29.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120236.png || $\beta : \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X F , \Omega ) \rightarrow \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X \backslash Y || F , \Omega )$ || $$ \beta : \operatorname { Ext } | + | | 33.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|29.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120236.png | ||
| + | || $\beta : \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X F , \Omega ) \rightarrow \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X \backslash Y | ||
| + | || F , \Omega )$ | ||
| + | ||$$\beta :\operatorname {Ext}_c^{n-p-1}(X;{\cal F},\Omega )\rightarrow \operatorname {Ext}_c^{n-p-1}(X\backslash Y ;{\cal F},\Omega ).$$ | ||
| + | || conf 0.634 | ||
| + | || F | ||
d034120236.png (236) | d034120236.png (236) | ||
|- | |- | ||
| − | | 34.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|77.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120247.png || $\underset { n \rightarrow \infty } { \operatorname { lim } } | \alpha _ { n } | ^ { 1 / n } = \sigma < + \infty$ || $$ \underset { n \rightarrow \infty } { \overline { \lim } } | \alpha _ | + | | 34.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|77.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120247.png | ||
| + | || $\underset { n \rightarrow \infty } { \operatorname { lim } } | \alpha _ { n } | ^ { 1 / n } = \sigma < + \infty$ | ||
| + | ||$$\underset {n\rightarrow \infty }{\overline {\lim }}|\alpha _ n|^{1/n}=\sigma <+\infty.$$ | ||
| + | || conf 0.521 F | ||
d034120247.png (247) | d034120247.png (247) | ||
|- | |- | ||
| − | | 35.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|58.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120253.png || $h ( \phi ) = \operatorname { lim } _ { r \rightarrow \infty } \frac { \operatorname { ln } | A ( r e ^ { i \phi } ) | } { r }$ || $$ h ( \phi ) = \underset { n\rightarrow \infty }{\overline{ \lim } } \frac { \operatorname { ln } | A ( | + | | 35.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|58.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120253.png | ||
| + | || $h ( \phi ) = \operatorname { lim } _ { r \rightarrow \infty } \frac { \operatorname { ln } | A ( r e ^ { i \phi } ) | } { r }$ | ||
| + | ||$$h(\phi )=\underset {n\rightarrow \infty }{\overline {\lim }}\frac {\operatorname {ln}|A(re^{i\phi })|}r$$ | ||
| + | || conf 0.861 F | ||
d034120253.png (253) | d034120253.png (253) | ||
|- | |- | ||
| − | | 36.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|69.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120360.png || $\operatorname { sup } _ { l \in E ^ { \perp } } | l ( \omega ) | = \operatorname { inf } _ { x \in E } \| \omega - x \|$ || $$ \operatorname* { sup } _ { l \in E^\perp \atop \|l\|\le 1 } | + | | 36.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|69.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120360.png | ||
| + | || $\operatorname { sup } _ { l \in E ^ { \perp } } | l ( \omega ) | = \operatorname { inf } _ { x \in E } \| \omega - x \|$ | ||
| + | ||$$\operatorname*{sup}_{l\in E^\perp \atop \|l\|\le 1 }|l(\omega )|=\operatorname*{inf}_{x\in E }\|\omega -x\|,$$ | ||
| + | || conf 0.293 F | ||
d034120360.png (360) | d034120360.png (360) | ||
|- | |- | ||
| − | | 37.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|15.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120376.png || $\operatorname { sup } _ { f \in B ^ { 1 } } | \int _ { \partial G } f ( \zeta ) \omega ( \zeta ) d \zeta | = \operatorname { inf } _ { \phi \in E ^ { 1 } } \int _ { \partial G } | \omega ( \zeta ) - \phi ( \zeta ) \| d \zeta |$ || $$ \operatorname* { sup } _ { f \in B ^ | + | | 37.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|15.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120376.png | ||
| + | || $\operatorname { sup } _ { f \in B ^ { 1 } } | \int _ { \partial G } f ( \zeta ) \omega ( \zeta ) d \zeta | = \operatorname { inf } _ { \phi \in E ^ { 1 } } \int _ { \partial G } | \omega ( \zeta ) - \phi ( \zeta ) \| d \zeta |$ | ||
| + | ||$$\operatorname*{sup}_{f\in B ^1}\big|\int\limits _ {\partial G }f(\zeta )\omega (\zeta )d\zeta \big|=\operatorname*{inf}_{\phi \in E ^1}\int\limits _ {\partial G }|\omega (\zeta )-\phi (\zeta ) | ||
| + | ||d\zeta |.$$ | ||
| + | || conf 0.508 | ||
d034120376.png (376) | d034120376.png (376) | ||
|- | |- | ||
| − | | 38.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|52.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120509.png || $f = \{ f _ { \alpha } \} \in \prod _ { \alpha } F _ { \alpha } , \quad g = \{ g _ { \alpha } \} \in \oplus _ { \alpha } G _ { \alpha }$ || $$ f = \{ | + | | 38.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|52.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120509.png | ||
| + | || $f = \{ f _ { \alpha } \} \in \prod _ { \alpha } F _ { \alpha } , \quad g = \{ g _ { \alpha } \} \in \oplus _ { \alpha } G _ { \alpha }$ | ||
| + | ||$$f=\{f_{\alpha }\}\in \prod _ {\alpha }F_{\alpha },\quad g =\{g_{\alpha }\}\in \operatorname*\oplus _ {\alpha }G_{\alpha }.$$ | ||
| + | || conf 0.491 | ||
d034120509.png (509) | d034120509.png (509) | ||
|- | |- | ||
| − | | 39.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|140.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120535.png || $f ^ { * } ( x ^ { * } ) = \operatorname { sup } _ { x \in X } ( \langle x ^ { * } , x \rangle - f ( x ) )$ || $$ f ^ { * } ( x ^ { * } ) = \operatorname*{ sup } _ { x \in X } ( \langle x ^ { * } , x \rangle - f ( x ) ) $$|| conf 0.900 | + | | 39.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|140.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120535.png | ||
| + | || $f ^ { * } ( x ^ { * } ) = \operatorname { sup } _ { x \in X } ( \langle x ^ { * } , x \rangle - f ( x ) )$ | ||
| + | ||$$f^{*}(x^{*})=\operatorname*{sup}_{x\in X }(\langle x ^{*},x\rangle -f(x))$$ | ||
| + | || conf 0.900 | ||
d034120535.png (535) | d034120535.png (535) | ||
|- | |- | ||
| − | | 40.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|94.]]) || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120555.png || $f _ { 0 } ( x ) \rightarrow \text { inf, } \quad f _ { i } ( x ) \leq 0 , \quad i = 1 , \ldots , m , \quad x \in B$ || $$ | + | | 40.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|94.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d034120555.png | ||
| + | || $f _ { 0 } ( x ) \rightarrow \text { inf, } \quad f _ { i } ( x ) \leq 0 , \quad i = 1 , \ldots , m , \quad x \in B$ | ||
| + | ||$$f_0(x)\rightarrow \text{ inf, }\quad f _ i(x)\leq 0 ,\quad i =1,\ldots ,m,\quad x \in B,$$ | ||
| + | || conf 0.810 | ||
d034120555.png (555) | d034120555.png (555) | ||
|- | |- | ||
| − | | 41.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|74.]])*|| https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412079.png || $( c _ { \gamma } , c ^ { r } ) = \sum _ { t ^ { r } \in K } c _ { r } ( t ^ { \prime } ) c ^ { r } ( t ^ { r } ) \operatorname { mod } 1$ || $$ ( | + | | 41.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|74.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/d/d034/d034120/d03412079.png | ||
| + | || $( c _ { \gamma } , c ^ { r } ) = \sum _ { t ^ { r } \in K } c _ { r } ( t ^ { \prime } ) c ^ { r } ( t ^ { r } ) \operatorname { mod } 1$ | ||
| + | ||$$(c_{\gamma },c^r)=\sum _ {t^r\in K }c_r(t^{\prime })c^r(t^r)\operatorname {mod}1$$ | ||
| + | || conf 0.117 F | ||
d03412079.png (79) | d03412079.png (79) | ||
| Line 276: | Line 513: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 42.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|63.]]) || https://www.encyclopediaofmath.org/legacyimages/e/e036/e036960/e03696024.png || $F _ { 1 } F _ { 2 } = F _ { 1 } \langle F _ { 2 } \rangle = F _ { 1 } ( F _ { 2 } ) = F _ { 2 } ( F _ { 1 } ) = F _ { 2 } \langle F _ { 1 } \rangle$ || | + | | 42.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|63.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/e/e036/e036960/e03696024.png | ||
| + | || $F _ { 1 } F _ { 2 } = F _ { 1 } \langle F _ { 2 } \rangle = F _ { 1 } ( F _ { 2 } ) = F _ { 2 } ( F _ { 1 } ) = F _ { 2 } \langle F _ { 1 } \rangle$ | ||
| + | ||$$F_1F_2=F_1\langle F _ 2\rangle =F_1(F_2)=F_2(F_1)=F_2\langle F _ 1\rangle,$$ | ||
| + | || conf 0.628 | ||
e03696024.png (24) | e03696024.png (24) | ||
| Line 291: | Line 532: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 43.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|120.]])*|| https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820118.png || $\operatorname { og } F _ { MU } ( X ) = \sum _ { i = 1 } ^ { \infty } i ^ { - 1 } [ C ^ { - } P ^ { - 1 } ] X ^ { i }$ || | + | | 43.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|120.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f040820118.png | ||
| + | || $\operatorname { og } F _ { MU } ( X ) = \sum _ { i = 1 } ^ { \infty } i ^ { - 1 } [ C ^ { - } P ^ { - 1 } ] X ^ { i }$ | ||
| + | ||$$\operatorname {log}F_{\rm MU }(X)=\sum _ {i=1}^{\infty }i^{-1}[{\rm CP}^{i-1}]X^i,$$ | ||
| + | || conf 0.098 F | ||
f040820118.png (118) | f040820118.png (118) | ||
|- | |- | ||
| − | | 44.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|147.]])*|| https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082059.png || $( x _ { 1 } , \ldots , x _ { x } ) \circ ( y _ { 1 } , \ldots , y _ { n } ) = ( z _ { 1 } , \ldots , z _ { x } )$ || | + | | 44.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|147.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/f/f040/f040820/f04082059.png | ||
| + | || $( x _ { 1 } , \ldots , x _ { x } ) \circ ( y _ { 1 } , \ldots , y _ { n } ) = ( z _ { 1 } , \ldots , z _ { x } )$ | ||
| + | ||$$(x_1,\ldots ,x_n)\circ (y_1,\ldots ,y_n)=(z_1,\ldots ,z_n),$$ | ||
| + | || conf 0.553 F | ||
f04082059.png (59) | f04082059.png (59) | ||
| Line 310: | Line 559: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 45.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|148.]]) || https://www.encyclopediaofmath.org/legacyimages/g/g130/g130020/g1300205.png || $\alpha ^ { \beta } = \operatorname { exp } \{ \beta \operatorname { log } \alpha \}$ || | + | | 45.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|148.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/g/g130/g130020/g1300205.png | ||
| + | || $\alpha ^ { \beta } = \operatorname { exp } \{ \beta \operatorname { log } \alpha \}$ | ||
| + | ||$\alpha ^{\beta }=\operatorname {exp}\{\beta \operatorname {log}\alpha \}$ | ||
| + | || conf 0.979 | ||
g1300205.png (5) | g1300205.png (5) | ||
| Line 325: | Line 578: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 46.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|22.]])*|| https://www.encyclopediaofmath.org/legacyimages/g/g045/g045210/g04521075.png || $\left. \begin{array} { l l l } { A } & { \rightarrow Y } & { \square } \\ { \downarrow } & { \square } & { } & { \square } \\ { X } & { \square } & { } & { A } \end{array} \right.$ | + | | 46.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|22.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/g/g045/g045210/g04521075.png | ||
| + | || $\left. \begin{array} { l l l } { A } & { \rightarrow Y } & { \square } \\ { \downarrow } & { \square } & { } & { \square } \\ { X } & { \square } & { } & { A } \end{array} \right.$ | ||
| + | | style="text-align:center;"| source incomplete | ||
| + | || conf 0.226 F | ||
g04521075.png (75) | g04521075.png (75) | ||
| Line 340: | Line 597: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 47.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|89.]]) || https://www.encyclopediaofmath.org/legacyimages/h/h047/h047690/h04769069.png || $\mathfrak { g } = \mathfrak { f } + \mathfrak { m } , \quad \mathfrak { f } \cap \mathfrak { m } = \{ 0 \}$ || | + | | 47.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|89.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/h/h047/h047690/h04769069.png | ||
| + | || $\mathfrak { g } = \mathfrak { f } + \mathfrak { m } , \quad \mathfrak { f } \cap \mathfrak { m } = \{ 0 \}$ | ||
| + | ||$$\mathfrak g=\mathfrak f+\mathfrak m,\quad \mathfrak f\cap \mathfrak m=\{0\},$$ | ||
| + | || conf 0.793 | ||
h04769069.png (69) | h04769069.png (69) | ||
| Line 355: | Line 616: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 48.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|103.]]) || https://www.encyclopediaofmath.org/legacyimages/h/h047/h047970/h047970129.png || $m \circ ( \iota \otimes 1 ) \circ \mu = m \circ ( 1 \otimes \iota ) \circ \mu = e \circ \epsilon$ || $m \circ ( \iota \otimes 1 ) \circ \mu = m \circ ( 1 \otimes \iota ) \circ \mu = e \circ \epsilon$ | + | | 48.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|103.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/h/h047/h047970/h047970129.png | ||
| + | || $m \circ ( \iota \otimes 1 ) \circ \mu = m \circ ( 1 \otimes \iota ) \circ \mu = e \circ \epsilon$ | ||
| + | ||$m\circ (\iota \otimes 1 )\circ \mu =m\circ (1\otimes \iota )\circ \mu =e\circ \epsilon$ | ||
| + | || conf 0.618 | ||
h047970129.png (129) | h047970129.png (129) | ||
|- | |- | ||
| − | | 49.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|107.]])*|| https://www.encyclopediaofmath.org/legacyimages/h/h047/h047970/h047970139.png || $F _ { 1 } ( X || Y ) , \ldots , F _ { n } ( X || Y ) \in K [ X _ { 1 } , \ldots , X _ { n } || Y _ { 1 } , \ldots , Y _ { n } ] \}$ || $ | + | | 49.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|107.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/h/h047/h047970/h047970139.png | ||
| + | || $F _ { 1 } ( X | ||
| + | || Y ) , \ldots , F _ { n } ( X | ||
| + | || Y ) \in K [ X _ { 1 } , \ldots , X _ { n } | ||
| + | || Y _ { 1 } , \ldots , Y _ { n } ] \}$ | ||
| + | ||$F_1(X;Y),\ldots ,F_n(X;Y)\in K [X_1,\ldots ,X_n;Y_1,\ldots ,Y_n]\}$ | ||
| + | || conf 0.353 F | ||
h047970139.png (139) | h047970139.png (139) | ||
|- | |- | ||
| − | | 50.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|97.]]) || https://www.encyclopediaofmath.org/legacyimages/h/h047/h047970/h04797042.png || $\epsilon ( x ) = 0 , \quad \delta ( x ) = x \bigotimes 1 + 1 \bigotimes x , \quad x \in \mathfrak { g }$ || | + | | 50.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|97.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/h/h047/h047970/h04797042.png | ||
| + | || $\epsilon ( x ) = 0 , \quad \delta ( x ) = x \bigotimes 1 + 1 \bigotimes x , \quad x \in \mathfrak { g }$ | ||
| + | ||$$\epsilon (x)=0,\quad \delta (x)=x\otimes 1 +1\otimes x ,\quad x \in \mathfrak g.$$ | ||
| + | || conf 0.213 | ||
h04797042.png (42) | h04797042.png (42) | ||
| Line 378: | Line 654: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 51.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|149.]])*|| https://www.encyclopediaofmath.org/legacyimages/i/i052/i052350/i05235015.png || $\alpha _ { 1 } , \ldots , i _ { R } \rightarrow \alpha _ { 2 } ^ { \prime } , \ldots , i _ { R }$ || | + | | 51.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|149.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/i/i052/i052350/i05235015.png | ||
| + | || $\alpha _ { 1 } , \ldots , i _ { R } \rightarrow \alpha _ { 2 } ^ { \prime } , \ldots , i _ { R }$ | ||
| + | ||$$\alpha _ {i_1,\dots,i_n}\rightarrow \alpha _ {i_1,\dots,i_n}^{\prime }.$$ | ||
| + | || conf 0.142 F | ||
i05235015.png (15) | i05235015.png (15) | ||
| Line 393: | Line 673: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 52.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|150.]]) || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427030.png || $H ( C _ { 3 } , \Gamma ) = \{ X \in C _ { 3 } : X = \Gamma ^ { - 1 } X \square ^ { \prime } \Gamma \}$ || | + | | 52.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|150.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427030.png | ||
| + | || $H ( C _ { 3 } , \Gamma ) = \{ X \in C _ { 3 } : X = \Gamma ^ { - 1 } X \square ^ { \prime } \Gamma \}$ | ||
| + | ||$$(C_3,\Gamma )=\big\{X\in C _ 3:X=\Gamma ^{-1}X\square ^{\prime }\Gamma \big\},$$ | ||
| + | || conf 0.651 | ||
j05427030.png (30) | j05427030.png (30) | ||
|- | |- | ||
| − | | 53.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|42.]]) || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427031.png || $\Gamma = \operatorname { diag } \{ \gamma _ { 1 } , \gamma _ { 2 } , \gamma _ { 3 } \} , \quad \gamma _ { i } \neq 0 , \quad \gamma _ { i } \in F$ || | + | | 53.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|42.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427031.png | ||
| + | || $\Gamma = \operatorname { diag } \{ \gamma _ { 1 } , \gamma _ { 2 } , \gamma _ { 3 } \} , \quad \gamma _ { i } \neq 0 , \quad \gamma _ { i } \in F$ | ||
| + | ||$$\Gamma =\operatorname {diag}\{\gamma _ 1,\gamma _ 2,\gamma _ 3\},\quad \gamma _ i\neq 0 ,\quad \gamma _ i\in F,$$ | ||
| + | || conf 0.987 | ||
j05427031.png (31) | j05427031.png (31) | ||
|- | |- | ||
| − | | 54.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|125.]])*|| https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427077.png || $\mathfrak { g } = \mathfrak { g } - 1 + \mathfrak { g } \mathfrak { d } + \mathfrak { g } _ { 1 }$ || $\mathfrak | + | | 54.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|125.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427077.png | ||
| + | || $\mathfrak { g } = \mathfrak { g } - 1 + \mathfrak { g } \mathfrak { d } + \mathfrak { g } _ { 1 }$ | ||
| + | ||$\mathfrak g=\mathfrak g_{-1}+\mathfrak g_0+\mathfrak g_1$ | ||
| + | || conf 0.598 F | ||
j05427077.png (77) | j05427077.png (77) | ||
| Line 416: | Line 708: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 55.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|6.]])*|| https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543403.png || $J = \left| \begin{array} { c c c c } { J _ { n _ { 1 } } ( \lambda _ { 1 } ) } & { \square } & { \square } & { \square } \\ { \square } & { \ldots } & { \square } & { 0 } \\ { 0 } & { \square } & { \ldots } & { \square } \\ { \square } & { \square } & { \square } & { J _ { n _ { S } } ( \lambda _ { s } ) } \end{array} \right|$ || | + | | 55.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|6.]])* |
| − | J_{n_1}(\lambda_1) | + | || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543403.png |
| − | + | || $J = \left| \begin{array} { c c c c } { J _ { n _ { 1 } } ( \lambda _ { 1 } ) } & { \square } & { \square } & { \square } \\ { \square } & { \ldots } & { \square } & { 0 } \\ { 0 } & { \square } & { \ldots } & { \square } \\ { \square } & { \square } & { \square } & { J _ { n _ { S } } ( \lambda _ { s } ) } \end{array} \right|$ | |
| − | + | ||$$J=\left\| | |
| − | + | \begin {array}{cccc} | |
| − | \end{array} \right\|,$$ || conf 0.072 F | + | |
| + | J_{n_1}(\lambda_1) &0 &0 &0\\ | ||
| + | |||
| + | 0 &\ddots &\ddots &0\\ | ||
| + | |||
| + | 0 &\ddots &\ddots &0\\ | ||
| + | |||
| + | 0 &0 &0 &J_{n_s}(\lambda_s) | ||
| + | |||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.072 F | ||
j0543403.png (3) | j0543403.png (3) | ||
|- | |- | ||
| − | | 56.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|64.]]) || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434030.png || $C _ { m } ( \lambda ) = \operatorname { rk } ( A - \lambda E ) ^ { m - 1 } - 2 \operatorname { rk } ( A - \lambda E ) ^ { m } +$ || $$ | + | | 56.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|64.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j05434030.png | ||
| + | || $C _ { m } ( \lambda ) = \operatorname { rk } ( A - \lambda E ) ^ { m - 1 } - 2 \operatorname { rk } ( A - \lambda E ) ^ { m } +$ | ||
| + | ||$$C_m(\lambda )=\operatorname {rk}(A-\lambda E )^{m-1}-2\operatorname {rk}(A-\lambda E )^m+$$ | ||
| + | || conf 0.955 | ||
j05434030.png (30) | j05434030.png (30) | ||
|- | |- | ||
| − | | 57.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|1.]])*|| https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543406.png || $J _ { m } ( \lambda ) = \| \begin{array} { c c c c c c } { \lambda } & { 1 } & { \square } & { \square } & { \square } & { \square } \\ { \square } & { \lambda } & { 1 } & { \square } & { 0 } & { \square } \\ { \square } & { \square } & { \cdots } & { \square } & { \square } & { \square } \\ { \square } & { \square } & { \square } & { \cdots } & { \square } & { \square } \\ { \square } & { 0 } & { \square } & { \square } & { \lambda } & { 1 } \\ { \square } & { \square } & { \square } & { \square } & { \square } & { \lambda } \end{array} ]$ || $$J_m(\lambda) = \left\| \begin{array} { | + | | 57.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|1.]])* |
| − | \lambda & | + | || https://www.encyclopediaofmath.org/legacyimages/j/j054/j054340/j0543406.png |
| − | \square & \lambda & | + | || $J _ { m } ( \lambda ) = \| \begin{array} { c c c c c c } { \lambda } & { 1 } & { \square } & { \square } & { \square } & { \square } \\ { \square } & { \lambda } & { 1 } & { \square } & { 0 } & { \square } \\ { \square } & { \square } & { \cdots } & { \square } & { \square } & { \square } \\ { \square } & { \square } & { \square } & { \cdots } & { \square } & { \square } \\ { \square } & { 0 } & { \square } & { \square } & { \lambda } & { 1 } \\ { \square } & { \square } & { \square } & { \square } & { \square } & { \lambda } \end{array} ]$ |
| − | \square & \square & \ddots | + | ||$$J_m(\lambda)=\left\| |
| − | \square & \square & \square & | + | \begin {array}{cccccc} |
| − | \square & | + | |
| − | \square & \square & \square & | + | \lambda &1 &\square &\square &\square &\square \\ |
| − | \end{array} \right\|,$$ || conf 0.098 F | + | |
| + | \square &\lambda &1 &\square &0 &\square \\ | ||
| + | |||
| + | \square &\square &\ddots &\ddots &\square &\square\\ | ||
| + | |||
| + | \square &\square &\square &\ddots &\ddots &\square \\ | ||
| + | |||
| + | \square &0 &\square &\square &\lambda &1\\ | ||
| + | |||
| + | \square &\square &\square &\square &\square &\lambda | ||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.098 F | ||
j0543406.png (6) | j0543406.png (6) | ||
| Line 450: | Line 769: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 58.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|5.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510127.png || $\left\| \begin{array} { r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } \end{array} \right\|$ || $$B_n: \quad \left\| \begin{array} { | + | | 58.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|5.]]) |
| − | + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510127.png | |
| − | { - 1 } & | + | || $\left\| \begin{array} { r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } \end{array} \right\|$ |
| − | + | ||$$B_n:\quad \left\| | |
| − | \cdot | + | \begin {array}{rrrrrr} |
| − | + | ||
| − | + | 2 &{-1} &0 &{\dots } &0 &0\\ | |
| − | + | ||
| − | \end{array} \right\|,$$|| conf 0.232 | + | {-1} &2 &{-1} &{\dots } &0 &0\\ |
| + | |||
| + | 0 &{-1} &2 &{\dots } &0 &0\\ | ||
| + | |||
| + | \cdot &\cdot &\cdot &\dots &\cdot &\cdot \\ | ||
| + | |||
| + | 0 &0 &0 &{\dots } &{-1} &0\\ | ||
| + | |||
| + | 0 &0 &0 &{\dots } &2 &{-2}\\ | ||
| + | |||
| + | 0 &0 &0 &{\dots } &{-1} &2 | ||
| + | |||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.232 | ||
l058510127.png (127) | l058510127.png (127) | ||
|- | |- | ||
| − | | 59.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|3.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510129.png || $\| \left. \begin{array} { r r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } & { - 1 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 2 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 0 } & { 2 } \end{array} \right. |$ || | + | | 59.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|3.]])* |
| − | \left\| \begin{array} { | + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510129.png |
| − | + | || $\| \left. \begin{array} { r r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } & { - 1 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 2 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 0 } & { 2 } \end{array} \right. |$ | |
| − | { - 1 } & | + | ||$$D_n:\quad \left\| |
| − | + | \begin {array}{rrrrrrr} | |
| − | \cdot | + | |
| − | + | 2 &{-1} &0 &{\dots } &0 &0 &0 &0\\ | |
| − | + | ||
| − | + | {-1} &2 &{-1} &{\dots } &0 &0 &0 &0\\ | |
| − | + | ||
| − | \end{array} \right\|,$$ || conf 0.055 F | + | 0 &{-1} &2 &{\dots } &0 &0 &0 &0\\ |
| + | |||
| + | \cdot &\cdot &\cdot &\dots &\cdot &\cdot &\cdot &\cdot \\ | ||
| + | |||
| + | 0 &0 &0 &{\dots } &2 &{-1} &0 &0\\ | ||
| + | |||
| + | 0 &0 &0 &{\dots } &{-1} &2 &{-1} &{-1}\\ | ||
| + | |||
| + | 0 &0 &0 &{\dots } &0 &{-1} &2 &0\\ | ||
| + | |||
| + | 0 &0 &0 &{\dots } &0 &{-1} &0 &2 | ||
| + | |||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.055 F | ||
l058510129.png (129) | l058510129.png (129) | ||
|- | |- | ||
| − | | 60.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|8.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510130.png || $\left\| \begin{array} { r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$ || $$E_6: | + | | 60.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|8.]])* |
| − | \quad \left\| \begin{array} { | + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510130.png |
| − | + | || $\left\| \begin{array} { r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$ | |
| − | + | ||$$E_6: | |
| − | { - 1 } & | + | \quad \left\| |
| − | + | \begin {array}{rrrrrr} | |
| − | + | ||
| − | + | 2 &0 &{-1} &0 &0 &0\\ | |
| − | \end{array} \right\|,$$ || conf 0.628 F | + | |
| + | 0 &2 &0 &{-1} &0 &0\\ | ||
| + | |||
| + | {-1} &0 &2 &{-1} &0 &0\\ | ||
| + | |||
| + | 0 &{-1} &{-1} &2 &{-1} &0\\ | ||
| + | |||
| + | 0 &0 &0 &{-1} &2 &{-1}\\ | ||
| + | |||
| + | 0 &0 &0 &0 &{-1} &2 | ||
| + | |||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.628 F | ||
l058510130.png (130) | l058510130.png (130) | ||
|- | |- | ||
| − | | 61.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|4.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510131.png || $\left\| \begin{array} { r r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$ || $$E_7: \quad | + | | 61.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|4.]]) |
| − | \left\| \begin{array} { | + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510131.png |
| − | + | || $\left\| \begin{array} { r r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$ | |
| − | + | ||$$E_7:\quad \left\| | |
| − | {-1 } & | + | \begin {array}{rrrrrrr} |
| − | + | ||
| − | + | 2 &0 &{-1} &0 &0 &0 &0\\ | |
| − | + | ||
| − | + | 0 &2 &0 &{-1} &0 &0 &0\\ | |
| − | \end{array} \right\|,$$ || conf 0.278 | + | |
| + | {-1} &0 &2 &{-1} &0 &0 &0\\ | ||
| + | |||
| + | 0 &{-1} &{-1} &2 &{-1} &0 &0\\ | ||
| + | |||
| + | 0 &0 &0 &{-1} &2 &{-1} &0\\ | ||
| + | |||
| + | 0 &0 &0 &0 &{-1} &2 &{-1}\\ | ||
| + | |||
| + | 0 &0 &0 &0 &0 &{-1} &2 | ||
| + | |||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.278 | ||
l058510131.png (131) | l058510131.png (131) | ||
|- | |- | ||
| − | | 62.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|2.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510132.png || $\left. \begin{array} { r l l l l l l l } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right.$ || $$E_8: \quad | + | | 62.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|2.]])* |
| − | \left\| \begin{array} { | + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510132.png |
| − | + | || $\left. \begin{array} { r l l l l l l l } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right.$ | |
| − | + | ||$$E_8:\quad \left\| | |
| − | {-1 } & | + | \begin {array}{rrrrrrrr} |
| − | + | ||
| − | + | 2 &0 &{-1} &0 &0 &0 &0 & | |
| − | + | 0\\ | |
| − | + | 0 &2 &0 &{-1} &0 &0 &0 &0\\ | |
| − | + | ||
| − | \end{array} \right\|,$$ || conf 0.354 F | + | {-1} &0 &2 &{-1} &0 &0 &0 &0\\ |
| + | |||
| + | 0 &{-1} &{-1} &2 &{-1} &0 &0 &0\\ | ||
| + | |||
| + | 0 &0 &0 &{-1} &2 &{-1} &0 &0\\ | ||
| + | |||
| + | 0 &0 &0 &0 &{-1} &2 &{-1} &0\\ | ||
| + | |||
| + | 0 &0 &0 &0 &0 &{-1} &2 &{-1}\\ | ||
| + | |||
| + | 0 &0 &0 &0 &0 &0 &{-1} &2 | ||
| + | |||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.354 F | ||
l058510132.png (132) | l058510132.png (132) | ||
|- | |- | ||
| − | | 63.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|10.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510133.png || $\left\| \begin{array} { r r r r } { 2 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 2 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| , \quad G _ { 2 } : \quad \left\| \begin{array} { r r } { 2 } & { - 1 } \\ { - 3 } & { 2 } \end{array} \right\|$ | + | | 63.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|10.]])* |
| − | || $$F_4: \quad \left\| \begin{array} { | + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l058510133.png |
| + | || $\left\| \begin{array} { r r r r } { 2 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 2 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| , \quad G _ { 2 } : \quad \left\| \begin{array} { r r } { 2 } & { - 1 } \\ { - 3 } & { 2 } \end{array} \right\|$ | ||
| + | |||
| + | ||$$F_4:\quad \left\| | ||
| + | \begin {array}{rrrr} | ||
| + | 2 &{-1} &0 &0\\ | ||
| + | {-1} &2 &{-2} &0\\ | ||
| + | 0 &{-1} &2 &{-1}\\ | ||
| + | 0 &0 &{-1} &2 | ||
| + | \end {array} | ||
| + | \right\|,\quad G _ 2:\quad \left\| | ||
| + | \begin {array}{rr} | ||
| + | 2&{-1}\\ | ||
| + | {-3}&2 | ||
| + | \end {array} | ||
| + | \right\|.$$ | ||
| + | || conf 0.374 F | ||
l058510133.png (133) | l058510133.png (133) | ||
|- | |- | ||
| − | | 64.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|98.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851030.png || $\mathfrak { g } _ { \alpha } = \{ X \in \mathfrak { g } : [ H , X ] = \alpha ( H ) X , H \in \mathfrak { h } \}$ || $$ \mathfrak | + | | 64.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|98.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851030.png | ||
| + | || $\mathfrak { g } _ { \alpha } = \{ X \in \mathfrak { g } : [ H , X ] = \alpha ( H ) X , H \in \mathfrak { h } \}$ | ||
| + | ||$$\mathfrak g_{\alpha }=\{X\in \mathfrak g:[H,X]=\alpha (H)X,H\in \mathfrak h\}.$$ | ||
| + | || conf 0.976 | ||
l05851030.png (30) | l05851030.png (30) | ||
|- | |- | ||
| − | | 65.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|126.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851037.png || $\mathfrak { g } = \mathfrak { h } + \sum _ { \alpha \in \Sigma } \mathfrak { g } _ { \alpha }$ || $$ \mathfrak | + | | 65.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|126.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851037.png | ||
| + | || $\mathfrak { g } = \mathfrak { h } + \sum _ { \alpha \in \Sigma } \mathfrak { g } _ { \alpha }$ | ||
| + | ||$$\mathfrak g=\mathfrak h+\sum _ {\alpha \in \Sigma }\mathfrak g_{\alpha }.$$ | ||
| + | || conf 0.945 | ||
l05851037.png (37) | l05851037.png (37) | ||
|- | |- | ||
| − | | 66.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|61.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851044.png || $\mathfrak { g } _ { \alpha } = \operatorname { dim } [ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { - \alpha } ] = 1$ || $$ \mathfrak | + | | 66.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|61.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851044.png | ||
| + | || $\mathfrak { g } _ { \alpha } = \operatorname { dim } [ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { - \alpha } ] = 1$ | ||
| + | ||$$\mathfrak g_{\alpha }=\operatorname {dim}[\mathfrak g_{\alpha },\mathfrak g_{-\alpha }]=1.$$ | ||
| + | || conf 0.520 F | ||
l05851044.png (44) | l05851044.png (44) | ||
|- | |- | ||
| − | | 67.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|65.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851050.png || $[ H _ { \alpha } , X _ { \alpha } ] = 2 X _ { \alpha } \quad \text { and } \quad [ H _ { \alpha } , Y _ { \alpha } ] = - 2 Y _ { 0 }$ || $$ [ | + | | 67.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|65.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851050.png | ||
| + | || $[ H _ { \alpha } , X _ { \alpha } ] = 2 X _ { \alpha } \quad \text { and } \quad [ H _ { \alpha } , Y _ { \alpha } ] = - 2 Y _ { 0 }$ | ||
| + | ||$$[H_{\alpha },X_{\alpha }]=2X_{\alpha }\quad {\rm and }\quad [H_{\alpha },Y_{\alpha }]=-2Y_{\alpha }.$$ | ||
| + | || conf 0.539 F | ||
l05851050.png (50) | l05851050.png (50) | ||
|- | |- | ||
| − | | 68.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|70.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851051.png || $\beta ( H _ { \alpha } ) = \frac { 2 ( \alpha , \beta ) } { ( \alpha , \alpha ) } , \quad \alpha , \beta \in \Sigma$ || $$ \beta ( | + | | 68.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|70.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851051.png | ||
| + | || $\beta ( H _ { \alpha } ) = \frac { 2 ( \alpha , \beta ) } { ( \alpha , \alpha ) } , \quad \alpha , \beta \in \Sigma$ | ||
| + | ||$$\beta (H_{\alpha })=\frac {2(\alpha ,\beta )}{(\alpha ,\alpha )},\quad \alpha ,\beta \in \Sigma,$$ | ||
| + | || conf 0.997 | ||
l05851051.png (51) | l05851051.png (51) | ||
|- | |- | ||
| − | | 69.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|112.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851057.png || $[ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { \beta } ] = \mathfrak { g } _ { \alpha + \beta }$ || $$ [ \mathfrak | + | | 69.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|112.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851057.png | ||
| + | || $[ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { \beta } ] = \mathfrak { g } _ { \alpha + \beta }$ | ||
| + | ||$$[\mathfrak g_{\alpha },\mathfrak g_{\beta }]=\mathfrak g_{\alpha +\beta }$$ | ||
| + | || conf 0.917 | ||
l05851057.png (57) | l05851057.png (57) | ||
|- | |- | ||
| − | | 70.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|127.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851064.png || $H _ { \alpha _ { 1 } } , \ldots , H _ { \alpha _ { k } } , X _ { \alpha } \quad ( \alpha \in \Sigma )$ || $$ | + | | 70.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|127.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851064.png | ||
| + | || $H _ { \alpha _ { 1 } } , \ldots , H _ { \alpha _ { k } } , X _ { \alpha } \quad ( \alpha \in \Sigma )$ | ||
| + | ||$$H_{\alpha _ 1},\ldots ,H_{\alpha _ k},X_{\alpha }\quad (\alpha \in \Sigma )$$ | ||
| + | || conf 0.432 | ||
l05851064.png (64) | l05851064.png (64) | ||
|- | |- | ||
| − | | 71.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|113.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851069.png || $[ [ X _ { \alpha _ { i } } , X _ { - } \alpha _ { i } ] , X _ { - \alpha _ { j } } ] = - n ( i , j ) X _ { \alpha _ { j } }$ || $$ [ [ | + | | 71.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|113.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851069.png | ||
| + | || $[ [ X _ { \alpha _ { i } } , X _ { - } \alpha _ { i } ] , X _ { - \alpha _ { j } } ] = - n ( i , j ) X _ { \alpha _ { j } }$ | ||
| + | ||$$[[X_{\alpha _ i},X_{-}\alpha _ i],X_{-\alpha _ j}]=-n(i,j)X_{\alpha _ j},$$ | ||
| + | || conf 0.628 F | ||
l05851069.png (69) | l05851069.png (69) | ||
|- | |- | ||
| − | | 72.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|79.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851073.png || $n ( i , j ) = \alpha _ { j } ( H _ { i } ) = \frac { 2 ( \alpha _ { i } , \alpha _ { j } ) } { ( \alpha _ { j } , \alpha _ { j } ) }$ || $$ n ( i , j ) = \alpha _ | + | | 72.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|79.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851073.png | ||
| + | || $n ( i , j ) = \alpha _ { j } ( H _ { i } ) = \frac { 2 ( \alpha _ { i } , \alpha _ { j } ) } { ( \alpha _ { j } , \alpha _ { j } ) }$ | ||
| + | ||$$n(i,j)=\alpha _ j(H_i)=\frac {2(\alpha _ i,\alpha _ j)}{(\alpha _ j,\alpha _ j)}.$$ | ||
| + | || conf 0.992 | ||
l05851073.png (73) | l05851073.png (73) | ||
|- | |- | ||
| − | | 73.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|13.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851074.png || $[ X _ { \alpha } , X _ { \beta } ] = \left\{ \begin{array} { l l } { N _ { \alpha , \beta } X _ { \alpha + \beta } } & { \text { if } \alpha + \beta \in \Sigma } \\ { 0 } & { \text { if } \alpha + \beta \notin \Sigma } \end{array} \right.$ || $$ [ | + | | 73.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|13.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851074.png | ||
| + | || $[ X _ { \alpha } , X _ { \beta } ] = \left\{ \begin{array} { l l } { N _ { \alpha , \beta } X _ { \alpha + \beta } } & { \text { if } \alpha + \beta \in \Sigma } \\ { 0 } & { \text { if } \alpha + \beta \notin \Sigma } \end{array} \right.$ | ||
| + | ||$$[X_{\alpha },X_{\beta }]=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | {N_{\alpha ,\beta }X_{\alpha +\beta }} &{\text{ if }\alpha +\beta \in \Sigma,}\\ | ||
| + | 0 &{\text{ if }\alpha +\beta \notin \Sigma,} | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.988 | ||
l05851074.png (74) | l05851074.png (74) | ||
|- | |- | ||
| − | | 74.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|80.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851078.png || $N _ { \alpha , \beta } = - N _ { - \alpha , - \beta } \quad \text { and } \quad N _ { \alpha , \beta } = \pm ( p + 1 )$ || $$ | + | | 74.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|80.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851078.png | ||
| + | || $N _ { \alpha , \beta } = - N _ { - \alpha , - \beta } \quad \text { and } \quad N _ { \alpha , \beta } = \pm ( p + 1 )$ | ||
| + | ||$$N_{\alpha ,\beta }=-N_{-\alpha ,-\beta }\quad {\rm and }\quad N _ {\alpha ,\beta }=\pm (p+1),$$ | ||
| + | || conf 0.961 | ||
l05851078.png (78) | l05851078.png (78) | ||
|- | |- | ||
| − | | 75.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|85.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851085.png || $X _ { \alpha } - X _ { - \alpha } , \quad i ( X _ { \alpha } + X _ { - \alpha } ) \quad ( \alpha \in \Sigma _ { + } )$ || $$ iH_\alpha, | + | | 75.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|85.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058510/l05851085.png | ||
| + | || $X _ { \alpha } - X _ { - \alpha } , \quad i ( X _ { \alpha } + X _ { - \alpha } ) \quad ( \alpha \in \Sigma _ { + } )$ | ||
| + | ||$$iH_\alpha,X_{\alpha }-X_{-\alpha },\quad i (X_{\alpha }+X_{-\alpha })\quad (\alpha \in \Sigma _ {+})$$ | ||
| + | || conf 0.691 F | ||
l05851085.png (85) | l05851085.png (85) | ||
| Line 579: | Line 1,035: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 76.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|119.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058520/l05852011.png || $[ \mathfrak { g } _ { i } , \mathfrak { g } _ { i } ] \subset \mathfrak { g } _ { \mathfrak { i } } + 1$ || | + | | 76.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|119.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058520/l05852011.png | ||
| + | || $[ \mathfrak { g } _ { i } , \mathfrak { g } _ { i } ] \subset \mathfrak { g } _ { \mathfrak { i } } + 1$ | ||
| + | ||$[\mathfrak g_i,\mathfrak g_i]\subset \mathfrak g_{i+1}$ | ||
| + | || conf 0.276 F | ||
l05852011.png (11) | l05852011.png (11) | ||
|- | |- | ||
| − | | 77.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|141.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058520/l05852046.png || $\operatorname { dim } \mathfrak { g } _ { i } = \operatorname { dim } \mathfrak { g } - i$ || | + | | 77.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|141.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058520/l05852046.png | ||
| + | || $\operatorname { dim } \mathfrak { g } _ { i } = \operatorname { dim } \mathfrak { g } - i$ | ||
| + | ||$\operatorname {dim}\mathfrak g_i=\operatorname {dim}\mathfrak g-i$ | ||
| + | || conf 0.901 | ||
l05852046.png (46) | l05852046.png (46) | ||
| Line 598: | Line 1,062: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 78.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|62.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058590/l058590115.png || $( G ) \cong \operatorname { Aut } ( L ( G ) ) \quad \text { and } \quad L ( \operatorname { Aut } ( G ) ) \cong D ( L ( G ) )$ || | + | | 78.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|62.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058590/l058590115.png | ||
| + | || $( G ) \cong \operatorname { Aut } ( L ( G ) ) \quad \text { and } \quad L ( \operatorname { Aut } ( G ) ) \cong D ( L ( G ) )$ | ||
| + | ||$$\operatorname {Aut}(G)\cong \operatorname {Aut}(L(G))\quad {\rm and }\quad L (\operatorname {Aut}(G))\cong D (L(G)),$$ | ||
| + | || conf 0.693 F | ||
l058590115.png (115) | l058590115.png (115) | ||
|- | |- | ||
| − | | 79.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|50.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058590/l05859086.png || $( X , Y ) \rightarrow \operatorname { exp } ^ { - 1 } ( \operatorname { exp } X \operatorname { exp } Y ) , \quad X , Y \in L ( G )$ || | + | | 79.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|50.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058590/l05859086.png | ||
| + | || $( X , Y ) \rightarrow \operatorname { exp } ^ { - 1 } ( \operatorname { exp } X \operatorname { exp } Y ) , \quad X , Y \in L ( G )$ | ||
| + | ||$$(X,Y)\rightarrow \operatorname {exp}^{-1}(\operatorname {exp}X\operatorname {exp}Y),\quad X ,Y\in L (G),$$ | ||
| + | || conf 0.856 | ||
l05859086.png (86) | l05859086.png (86) | ||
| Line 617: | Line 1,089: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 80.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|121.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058610/l05861012.png || $J = \left\| \begin{array} { c c } { 0 } & { E _ { x } } \\ { - E _ { x } } & { 0 } \end{array} \right\|$ || | + | | 80.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|121.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058610/l05861012.png | ||
| + | || $J = \left\| \begin{array} { c c } { 0 } & { E _ { x } } \\ { - E _ { x } } & { 0 } \end{array} \right\|$ | ||
| + | ||$$J=\left\| | ||
| + | \begin {array}{cc} | ||
| + | 0 &{E_x}\\ | ||
| + | {-E_x} &0 | ||
| + | \end {array} | ||
| + | \right\|,$$ | ||
| + | || conf 0.364 F | ||
l05861012.png (12) | l05861012.png (12) | ||
| Line 632: | Line 1,113: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 81.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|83.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058660/l0586604.png || $N ( F ) = \{ g \in GL ( V ) : g v \equiv v \operatorname { mod } V _ { i } \text { for all } v \in V _ { i } , i \geq 1 \}$ || | + | | 81.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|83.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058660/l0586604.png | ||
| + | || $N ( F ) = \{ g \in GL ( V ) : g v \equiv v \operatorname { mod } V _ { i } \text { for all } v \in V _ { i } , i \geq 1 \}$ | ||
| + | ||$$N(F)=\{g\in GL (V):gv\equiv v \operatorname {mod}V_i\;\text{for all }v\in V _ i,\;i\geq 1 \}$$ | ||
| + | || conf 0.466 | ||
l0586604.png (4) | l0586604.png (4) | ||
| Line 647: | Line 1,132: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 82.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|35.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058680/l058680102.png || $L ( \mathfrak { g } ) \cong \Gamma _ { 0 } ( \mathfrak { u } ) \cap \mathfrak { h } ^ { \prime } / \Gamma _ { 0 } ( [ \mathfrak { k } , \mathfrak { k } ] )$ || $$ L ( \mathfrak | + | | 82.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|35.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058680/l058680102.png | ||
| + | || $L ( \mathfrak { g } ) \cong \Gamma _ { 0 } ( \mathfrak { u } ) \cap \mathfrak { h } ^ { \prime } / \Gamma _ { 0 } ( [ \mathfrak { k } , \mathfrak { k } ] )$ | ||
| + | ||$$L(\mathfrak g)\cong \Gamma _ 0(\mathfrak u)\cap \mathfrak h^{\prime }/\Gamma _ 0([\mathfrak k,\mathfrak k])$$ | ||
| + | || conf 0.659 F | ||
l058680102.png (102) | l058680102.png (102) | ||
|- | |- | ||
| − | | 83.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|81.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058680/l05868032.png || $\Gamma _ { 1 } = \Gamma _ { 1 } ( g ) = \{ X \in h : \alpha ( X ) \in 2 \pi i Z \text { for all } \alpha \in \Sigma \}$ || $$ \Gamma _ | + | | 83.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|81.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058680/l05868032.png | ||
| + | || $\Gamma _ { 1 } = \Gamma _ { 1 } ( g ) = \{ X \in h : \alpha ( X ) \in 2 \pi i Z \text { for all } \alpha \in \Sigma \}$ | ||
| + | ||$$\Gamma _ 1=\Gamma _ 1(g)=\{X\in h :\alpha (X)\in 2 \pi i {\mathbf Z}\;\text{for all }\alpha \in \Sigma \}.$$ | ||
| + | || conf 0.183 F | ||
l05868032.png (32) | l05868032.png (32) | ||
| Line 666: | Line 1,159: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 84.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|36.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058720/l05872026.png || $( \operatorname { ad } x ) ^ { n } y = \sum _ { j = 1 } ^ { n } ( - 1 ) ^ { j } \left( \begin{array} { c } { n } \\ { j } \end{array} \right) x ^ { n - j } y x ^ { j }$ || $$ ( \operatorname { ad } x ) ^ | + | | 84.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|36.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058720/l05872026.png | ||
| + | || $( \operatorname { ad } x ) ^ { n } y = \sum _ { j = 1 } ^ { n } ( - 1 ) ^ { j } \left( \begin{array} { c } { n } \\ { j } \end{array} \right) x ^ { n - j } y x ^ { j }$ | ||
| + | ||$$(\operatorname {ad}x)^ny=\sum _ {j=1}^n(-1)^j\left(\begin {array}cn\\ | ||
| + | j | ||
| + | \end {array} | ||
| + | \right)x^{n-j}yx^j$$ | ||
| + | || conf 0.356 | ||
l05872026.png (26) | l05872026.png (26) | ||
|- | |- | ||
| − | | 85.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|99.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058720/l05872078.png || $\pi ( x + y ) = \pi ( x ) + \pi ( y ) , \quad \pi ( \lambda x ) = \lambda ^ { p } \pi ( x ) , \quad \lambda \in k$ || $$ \pi ( x + y ) = \pi ( x ) + \pi ( y ) , \quad \pi ( \lambda x ) = \lambda ^ | + | | 85.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|99.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058720/l05872078.png | ||
| + | || $\pi ( x + y ) = \pi ( x ) + \pi ( y ) , \quad \pi ( \lambda x ) = \lambda ^ { p } \pi ( x ) , \quad \lambda \in k$ | ||
| + | ||$$\pi (x+y)=\pi (x)+\pi (y),\quad \pi (\lambda x )=\lambda ^p\pi (x),\quad \lambda \in k .$$ | ||
| + | || conf 0.964 | ||
l05872078.png (78) | l05872078.png (78) | ||
| Line 685: | Line 1,189: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 86.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|134.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876010.png || $y _ { i } = f _ { i } ( g _ { 1 } , \ldots , g _ { i } || x _ { 1 } , \ldots , x _ { n } ) , \quad i = 1 , \ldots , n$ || $$ | + | | 86.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|134.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876010.png | ||
| + | || $y _ { i } = f _ { i } ( g _ { 1 } , \ldots , g _ { i } | ||
| + | || x _ { 1 } , \ldots , x _ { n } ) , \quad i = 1 , \ldots , n$ | ||
| + | ||$$y_i=f_i(g_1,\ldots ,g_i;x_1,\ldots ,x_n),\quad i =1,\ldots ,n$$ | ||
| + | || conf 0.276 | ||
l05876010.png (10) | l05876010.png (10) | ||
|- | |- | ||
| − | | 87.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|86.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876016.png || $X _ { i } = \sum _ { j = 1 } ^ { n } \xi _ { i j } ( x ) \frac { \partial } { \partial x _ { j } } , \quad i = 1 , \ldots , r$ || $$ | + | | 87.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|86.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876016.png | ||
| + | || $X _ { i } = \sum _ { j = 1 } ^ { n } \xi _ { i j } ( x ) \frac { \partial } { \partial x _ { j } } , \quad i = 1 , \ldots , r$ | ||
| + | ||$$X_i=\sum _ {j=1}^n\xi _ {ij}(x)\frac {\partial }{\partial x _ j},\quad i =1,\ldots ,r,$$ | ||
| + | || conf 0.656 | ||
l05876016.png (16) | l05876016.png (16) | ||
|- | |- | ||
| − | | 88.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|66.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876030.png || $\frac { \partial f _ { j } } { \partial g _ { i } } ( g , x ) = \sum _ { k = 1 } ^ { r } \xi _ { k j } ( f ( g _ { s } x ) ) \psi _ { k i } ( g )$ || $$ \frac { \partial f _ | + | | 88.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|66.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876030.png | ||
| + | || $\frac { \partial f _ { j } } { \partial g _ { i } } ( g , x ) = \sum _ { k = 1 } ^ { r } \xi _ { k j } ( f ( g _ { s } x ) ) \psi _ { k i } ( g )$ | ||
| + | ||$$\frac {\partial f _ j}{\partial g _ i}(g,x)=\sum _ {k=1}^r\xi _ {kj}(f(g_sx))\psi _ {ki}(g),$$ | ||
| + | || conf 0.336 F | ||
l05876030.png (30) | l05876030.png (30) | ||
|- | |- | ||
| − | | 89.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|19.]])*|| https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876037.png || $\sum _ { k = 1 } ^ { N } ( \xi _ { i k } \frac { \partial \xi _ { j l } } { \partial x _ { k } } - \xi _ { j k } \frac { \partial \xi _ { i l } } { \partial x _ { k } } ) = \sum _ { k = 1 } ^ { r } c _ { i j } ^ { k } \xi _ { k l }$ || $$ \sum _ { k = 1 } ^ | + | | 89.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|19.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876037.png | ||
| + | || $\sum _ { k = 1 } ^ { N } ( \xi _ { i k } \frac { \partial \xi _ { j l } } { \partial x _ { k } } - \xi _ { j k } \frac { \partial \xi _ { i l } } { \partial x _ { k } } ) = \sum _ { k = 1 } ^ { r } c _ { i j } ^ { k } \xi _ { k l }$ | ||
| + | ||$$\sum _ {k=1}^N(\xi _ {ik}\frac {\partial \xi _ {jl}}{\partial x _ k}-\xi _ {jk}\frac {\partial \xi _ {il}}{\partial x _ k})=\sum _ {k=1}^rc_{ij}^k\xi _ {kl},$$ | ||
| + | || conf 0.157 F | ||
l05876037.png (37) | l05876037.png (37) | ||
|- | |- | ||
| − | | 90.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|14.]]) || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876052.png || $\left. \begin{array} { c } { c _ { i j } ^ { k } = - c _ { j i } ^ { k } } \\ { \sum _ { l = 1 } ^ { r } ( c _ { i l } ^ { m } c _ { j k } ^ { l } + c _ { k l } ^ { m } c _ { i j } ^ { l } + c _ { j l } ^ { m } c _ { k i } ^ { l } ) = 0 , \quad 1 \leq i , j , k , l , m \leq r } \end{array} \right.$ || $$ \left. \begin{array} | + | | 90.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|14.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/l/l058/l058760/l05876052.png | ||
| + | || $\left. \begin{array} { c } { c _ { i j } ^ { k } = - c _ { j i } ^ { k } } \\ { \sum _ { l = 1 } ^ { r } ( c _ { i l } ^ { m } c _ { j k } ^ { l } + c _ { k l } ^ { m } c _ { i j } ^ { l } + c _ { j l } ^ { m } c _ { k i } ^ { l } ) = 0 , \quad 1 \leq i , j , k , l , m \leq r } \end{array} \right.$ | ||
| + | ||$$\left.\begin {array}c{c_{ij}^k=-c_{ji}^k},\\ | ||
| + | {\displaystyle\sum _ {l=1}^r(c_{il}^mc_{jk}^l+c_{kl}^mc_{ij}^l+c_{jl}^mc_{ki}^l)=0,\quad 1 \leq i ,j,k,l,m\leq r,} | ||
| + | \end {array} | ||
| + | \right\}$$ | ||
| + | || conf 0.085 | ||
l05876052.png (52) | l05876052.png (52) | ||
| Line 716: | Line 1,244: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 91.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|95.]]) || https://www.encyclopediaofmath.org/legacyimages/m/m063/m063010/m06301072.png || $F ( x _ { 1 } f _ { 1 } + \ldots + x _ { x } f _ { n } ) = x _ { 1 } x _ { n } + x _ { 2 } x _ { n } - 1 + \ldots + x _ { p } x _ { n } - p + 1$ || | + | | 91.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|95.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/m/m063/m063010/m06301072.png | ||
| + | || $F ( x _ { 1 } f _ { 1 } + \ldots + x _ { x } f _ { n } ) = x _ { 1 } x _ { n } + x _ { 2 } x _ { n } - 1 + \ldots + x _ { p } x _ { n } - p + 1$ | ||
| + | ||$$F(x_1f_1+\ldots +x_xf_n)=x_1x_n+x_2x_{n-1}+\ldots +x_px_{n-p+1},$$ | ||
| + | || conf 0.198 | ||
m06301072.png (72) | m06301072.png (72) | ||
| Line 731: | Line 1,263: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 92.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|114.]])*|| https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n066900110.png || $\phi ( g _ { 1 } ) \phi ( g ) \phi ( g _ { 1 } g _ { 2 } ) ^ { - 1 } = \operatorname { Int } m ( g _ { 1 } , g _ { 2 } )$ || $$ \phi ( | + | | 92.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|114.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n066900110.png | ||
| + | || $\phi ( g _ { 1 } ) \phi ( g ) \phi ( g _ { 1 } g _ { 2 } ) ^ { - 1 } = \operatorname { Int } m ( g _ { 1 } , g _ { 2 } )$ | ||
| + | ||$$\phi (g_1)\phi (g_2)\phi (g_1g_2)^{-1}=\operatorname {Int}m(g_1,g_2),$$ | ||
| + | || conf 0.443 F | ||
n066900110.png (110) | n066900110.png (110) | ||
|- | |- | ||
| − | | 93.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|90.]])*|| https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n066900118.png || $( g _ { 1 } , g _ { 2 } ) = h ( g _ { 1 } ) ( \phi ( g _ { 1 } ) ( h ( g _ { 2 } ) ) ) m ( g _ { 1 } , g _ { 2 } ) h ( g _ { 1 } , g _ { 2 } ) ^ { - 1 }$ || $$ m'( | + | | 93.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|90.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n066900118.png | ||
| + | || $( g _ { 1 } , g _ { 2 } ) = h ( g _ { 1 } ) ( \phi ( g _ { 1 } ) ( h ( g _ { 2 } ) ) ) m ( g _ { 1 } , g _ { 2 } ) h ( g _ { 1 } , g _ { 2 } ) ^ { - 1 }$ | ||
| + | ||$$m'(g_1,g_2)=h(g_1)(\phi (g_1)(h(g_2)))m(g_1,g_2)h(g_1,g_2)^{-1}.$$ | ||
| + | || conf 0.764 F | ||
n066900118.png (118) | n066900118.png (118) | ||
|- | |- | ||
| − | | 94.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|44.]]) || https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n06690016.png || $\delta ( e ) = e \quad \text { and } \quad \delta ( \rho ( a ) b ) = \sigma ( a ) \delta ( b ) , \quad \alpha \in C ^ { 0 } , \quad b \in C ^ { 1 }$ || $$ \delta ( e ) = e \quad \;\text {and } \quad \delta ( \rho ( a ) b ) = \sigma ( a ) \delta ( b ) , \quad \alpha \in C ^ | + | | 94.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|44.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n06690016.png | ||
| + | || $\delta ( e ) = e \quad \text { and } \quad \delta ( \rho ( a ) b ) = \sigma ( a ) \delta ( b ) , \quad \alpha \in C ^ { 0 } , \quad b \in C ^ { 1 }$ | ||
| + | ||$$\delta (e)=e\quad \;\text{and }\quad \delta (\rho (a)b)=\sigma (a)\delta (b),\quad \alpha \in C ^0,\quad b \in C ^1,$$ | ||
| + | || conf 0.400 | ||
n06690016.png (16) | n06690016.png (16) | ||
|- | |- | ||
| − | | 95.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|60.]])*|| https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n06690028.png || $C ^ { * } ( \mathfrak { U } , F ) = ( C ^ { 0 } ( \mathfrak { U } , F ) , C ^ { 1 } ( \mathfrak { U } , F ) , C ^ { 2 } ( \mathfrak { U } , F ) )$ || $$ C ^ { * } ( \mathfrak | + | | 95.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|60.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/n/n066/n066900/n06690028.png | ||
| + | || $C ^ { * } ( \mathfrak { U } , F ) = ( C ^ { 0 } ( \mathfrak { U } , F ) , C ^ { 1 } ( \mathfrak { U } , F ) , C ^ { 2 } ( \mathfrak { U } , F ) )$ | ||
| + | ||$$C^{*}(\mathfrak U,{\cal F})=(C^0(\mathfrak U,{\cal F}),C^1(\mathfrak U,{\cal F}),C^2(\mathfrak U,{\cal F})),$$ | ||
| + | || conf 0.205 F | ||
n06690028.png (28) | n06690028.png (28) | ||
| Line 758: | Line 1,306: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 96.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|39.]])*|| https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267025.png || $\operatorname { Pic } _ { X / k } ( S ^ { \prime } ) = \operatorname { Fic } ( X \times k S ^ { \prime } ) / \operatorname { Fic } ( S ^ { \prime } )$ || $$ \operatorname { Pic } _ { X / k } ( S ^ { \prime } ) = \operatorname { Pic } ( X \times_k S ^ { \prime } ) / \operatorname { Pic } ( S ^ { \prime } ) $$|| conf 0.345 F + | + | | 96.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|39.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/p/p072/p072670/p07267025.png | ||
| + | || $\operatorname { Pic } _ { X / k } ( S ^ { \prime } ) = \operatorname { Fic } ( X \times k S ^ { \prime } ) / \operatorname { Fic } ( S ^ { \prime } )$ | ||
| + | ||$$\operatorname {Pic}_{X/k}(S^{\prime })=\operatorname {Pic}(X\times_k S ^{\prime })/\operatorname {Pic}(S^{\prime })$$ | ||
| + | || conf 0.345 F + | ||
p07267025.png (25) | p07267025.png (25) | ||
| Line 772: | Line 1,324: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 97.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|100.]])*|| https://www.encyclopediaofmath.org/legacyimages/p/p074/p074640/p07464025.png || $g j : U _ { i } \cap U _ { j } \rightarrow G , \quad i , j \in I , \quad U _ { i } \cap U _ { j } \neq \emptyset$ || $$ g_j : | + | | 97.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|100.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/p/p074/p074640/p07464025.png | ||
| + | || $g j : U _ { i } \cap U _ { j } \rightarrow G , \quad i , j \in I , \quad U _ { i } \cap U _ { j } \neq \emptyset$ | ||
| + | ||$$g_j:U_i\cap U _ j\rightarrow G ,\quad i ,j\in I ,\quad U _ i\cap U _ j\neq \emptyset,$$ | ||
| + | || conf 0.184 F | ||
p07464025.png (25) | p07464025.png (25) | ||
| Line 786: | Line 1,342: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 98.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|101.]]) || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631062.png || $\phi ^ { * } : \mathfrak { g } ^ { * } \otimes \mathfrak { g } ^ { * } \rightarrow \mathfrak { g } ^ { * }$ || $$ \phi ^ { * } : \mathfrak | + | | 98.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|101.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631062.png | ||
| + | || $\phi ^ { * } : \mathfrak { g } ^ { * } \otimes \mathfrak { g } ^ { * } \rightarrow \mathfrak { g } ^ { * }$ | ||
| + | ||$$\phi ^{*}:\mathfrak g^{*}\otimes \mathfrak g^{*}\rightarrow \mathfrak g^{*}$$ | ||
| + | || conf 0.837 | ||
q07631062.png (62) | q07631062.png (62) | ||
|- | |- | ||
| − | | 99.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|108.]]) || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631071.png || $\delta : U _ { \mathfrak { g } } \rightarrow U _ { \mathfrak { g } } \otimes U _ { \mathfrak { g } }$ || $$ \delta : | + | | 99.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|108.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631071.png | ||
| + | || $\delta : U _ { \mathfrak { g } } \rightarrow U _ { \mathfrak { g } } \otimes U _ { \mathfrak { g } }$ | ||
| + | ||$$\delta :U_{\mathfrak g}\rightarrow U _ {\mathfrak g}\otimes U _ {\mathfrak g}$$ | ||
| + | || conf 0.648 | ||
q07631071.png (71) | q07631071.png (71) | ||
|- | |- | ||
| − | | 100.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|56.]])*|| https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631072.png || $\delta ( \alpha ) = \operatorname { lim } _ { h \rightarrow 0 } h ^ { - 1 } ( \Delta ( a ) - \Delta ^ { \prime } ( \alpha ) )$ || $$ \delta ( \alpha ) = \operatorname { lim } _ { h \rightarrow 0 } h ^ { - 1 } ( \Delta ( a ) - \Delta ^ { \prime } ( \alpha ) ) $$|| conf 0.304 F | + | | 100.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|56.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631072.png | ||
| + | || $\delta ( \alpha ) = \operatorname { lim } _ { h \rightarrow 0 } h ^ { - 1 } ( \Delta ( a ) - \Delta ^ { \prime } ( \alpha ) )$ | ||
| + | ||$$\delta (\alpha )=\operatorname {lim}_{h\rightarrow 0 }h^{-1}(\Delta (a)-\Delta ^{\prime }(\alpha ))$$ | ||
| + | || conf 0.304 F | ||
q07631072.png (72) | q07631072.png (72) | ||
|- | |- | ||
| − | | 101.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|129.]])*|| https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631088.png || $[ \alpha , X _ { i } ^ { \pm } ] = \pm \alpha _ { i } ( \alpha ) X _ { i } ^ { \pm } \quad \text { for } a$ || $$ [ \alpha , | + | | 101.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|129.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631088.png | ||
| + | || $[ \alpha , X _ { i } ^ { \pm } ] = \pm \alpha _ { i } ( \alpha ) X _ { i } ^ { \pm } \quad \text { for } a$ | ||
| + | ||$$[\alpha ,X_i^{\pm }]=\pm \alpha _ i(\alpha )X_i^{\pm }\quad \text{for }a\in \mathfrak h;$$ | ||
| + | || conf 0.544 F | ||
q07631088.png (88) | q07631088.png (88) | ||
|- | |- | ||
| − | | 102.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|128.]]) || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631089.png || $[ X _ { i } ^ { + } , X _ { j } ^ { - } ] = 2 \delta _ { i j } h ^ { - 1 } \operatorname { sinh } ( h H _ { i } / 2 )$ || $$ [ | + | | 102.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|128.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631089.png | ||
| + | || $[ X _ { i } ^ { + } , X _ { j } ^ { - } ] = 2 \delta _ { i j } h ^ { - 1 } \operatorname { sinh } ( h H _ { i } / 2 )$ | ||
| + | ||$$[X_i^{+},X_j^{-}]=2\delta _ {ij}h^{-1}\operatorname {sinh}(hH_i/2).$$ | ||
| + | || conf 0.893 | ||
q07631089.png (89) | q07631089.png (89) | ||
|- | |- | ||
| − | | 103.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|20.]]) || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631092.png || $\sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) q ^ { - k ( n - k ) / 2 } ( X _ { i } ^ { \pm } ) ^ { k } X _ { j } ^ { \pm } \cdot ( X _ { i } ^ { \pm } ) ^ { n - k } = 0$ || $$ \sum _ { k = 0 } ^ | + | | 103.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|20.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631092.png | ||
| + | || $\sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) q ^ { - k ( n - k ) / 2 } ( X _ { i } ^ { \pm } ) ^ { k } X _ { j } ^ { \pm } \cdot ( X _ { i } ^ { \pm } ) ^ { n - k } = 0$ | ||
| + | ||$$\sum _ {k=0}^n(-1)^k\left(\begin {array}ln\\ | ||
| + | k | ||
| + | \end {array} | ||
| + | \right)q^{-k(n-k)/2}(X_i^{\pm })^kX_j^{\pm }\cdot (X_i^{\pm })^{n-k}=0.$$ | ||
| + | || conf 0.055 | ||
q07631092.png (92) | q07631092.png (92) | ||
|- | |- | ||
| − | | 104.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|30.]]) || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631095.png || $\left( \begin{array} { l } { n } \\ { k } \end{array} \right) _ { q } = \frac { ( q ^ { n } - 1 ) \ldots ( q ^ { n - k + 1 } - 1 ) } { ( q ^ { k } - 1 ) \ldots ( q - 1 ) }$ || $$ \left( \begin{array} | + | | 104.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|30.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631095.png | ||
| + | || $\left( \begin{array} { l } { n } \\ { k } \end{array} \right) _ { q } = \frac { ( q ^ { n } - 1 ) \ldots ( q ^ { n - k + 1 } - 1 ) } { ( q ^ { k } - 1 ) \ldots ( q - 1 ) }$ | ||
| + | ||$$\left( | ||
| + | \begin {array}ln\\ | ||
| + | k | ||
| + | \end {array} | ||
| + | \right)_q=\frac {(q^n-1)\ldots (q^{n-k+1}-1)}{(q^k-1)\ldots (q-1)} | ||
| + | .$$ | ||
| + | || conf 0.443 | ||
q07631095.png (95) | q07631095.png (95) | ||
|- | |- | ||
| − | | 105.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|21.]])*|| https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631099.png || $\Delta ( X _ { i } ^ { \pm } ) = X _ { i } ^ { \pm } \bigotimes \operatorname { exp } ( \frac { h H _ { i } } { 4 } ) + \operatorname { exp } ( \frac { - h H _ { i } } { 4 } ) \otimes x _ { i } ^ { \pm }$ || $$ \Delta ( | + | | 105.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|21.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/q/q076/q076310/q07631099.png | ||
| + | || $\Delta ( X _ { i } ^ { \pm } ) = X _ { i } ^ { \pm } \bigotimes \operatorname { exp } ( \frac { h H _ { i } } { 4 } ) + \operatorname { exp } ( \frac { - h H _ { i } } { 4 } ) \otimes x _ { i } ^ { \pm }$ | ||
| + | ||$$\Delta (X_i^{\pm })=X_i^{\pm }\otimes \operatorname {exp}(\frac {hH_i}4)+\operatorname {exp}(\frac {-hH_i}4)\otimes X _ i^{\pm }.$$ | ||
| + | || conf 0.212 F | ||
q07631099.png (99) | q07631099.png (99) | ||
| Line 828: | Line 1,424: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 106.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|91.]]) || https://www.encyclopediaofmath.org/legacyimages/r/r077/r077630/r077630100.png || $0 \leq \frac { 2 ( \chi , \alpha ) } { ( \alpha , \alpha ) } < p \quad \text { for all } \alpha \in \Delta$ || $$ 0 \leq \frac { 2 ( \chi , \alpha ) } { ( \alpha , \alpha ) } < p \quad \text {for all } \alpha \in \Delta. $$|| conf 0.879 | + | | 106.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|91.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/r/r077/r077630/r077630100.png | ||
| + | || $0 \leq \frac { 2 ( \chi , \alpha ) } { ( \alpha , \alpha ) } < p \quad \text { for all } \alpha \in \Delta$ | ||
| + | ||$$0\leq \frac {2(\chi ,\alpha )}{(\alpha ,\alpha )}<p\quad \text{for all }\alpha \in \Delta.$$ | ||
| + | || conf 0.879 | ||
r077630100.png (100) | r077630100.png (100) | ||
|- | |- | ||
| − | | 107.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|135.]]) || https://www.encyclopediaofmath.org/legacyimages/r/r077/r077630/r077630104.png || $\phi _ { 0 } \bigotimes \phi _ { 1 } ^ { Fr } \otimes \ldots \otimes \phi _ { d } ^ { FF ^ { d } }$ || $$ \phi _ | + | | 107.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|135.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/r/r077/r077630/r077630104.png | ||
| + | || $\phi _ { 0 } \bigotimes \phi _ { 1 } ^ { Fr } \otimes \ldots \otimes \phi _ { d } ^ { FF ^ { d } }$ | ||
| + | ||$$\phi _ 0\otimes \phi _ 1^{Fr}\otimes \ldots \otimes \phi _ d^{{Fr}^d},$$ | ||
| + | || conf 0.136 | ||
r077630104.png (104) | r077630104.png (104) | ||
|- | |- | ||
| − | | 108.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|45.]])*|| https://www.encyclopediaofmath.org/legacyimages/r/r077/r077630/r07763055.png || $\chi = \delta _ { \phi } - \sum _ { \alpha \in \Delta } m _ { \alpha } \alpha , \quad m _ { \alpha } \in Z , \quad m _ { \alpha } \geq 0$ || $$ \chi = \delta _ { \phi } - \sum _ { \alpha \in \Delta } | + | | 108.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|45.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/r/r077/r077630/r07763055.png | ||
| + | || $\chi = \delta _ { \phi } - \sum _ { \alpha \in \Delta } m _ { \alpha } \alpha , \quad m _ { \alpha } \in Z , \quad m _ { \alpha } \geq 0$ | ||
| + | ||$$\chi =\delta _ {\phi }-\sum _ {\alpha \in \Delta }m_{\alpha }\alpha ,\quad m _ {\alpha }\in Z ,\quad m _ {\alpha }\geq 0.$$ | ||
| + | || conf 0.862 F | ||
r07763055.png (55) | r07763055.png (55) | ||
| Line 850: | Line 1,458: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 109.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|31.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590225.png || $\sum _ { k _ { 1 } , \ldots , k _ { n } = 0 } ^ { \infty } c _ { k _ { 1 } \cdots k _ { n } } ( z _ { 1 } - \zeta _ { 1 } ) ^ { k _ { 1 } } \ldots ( z _ { n } - \zeta _ { n } ) ^ { k _ { n } }$ || $$ \sum _ { | + | | 109.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|31.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590225.png | ||
| + | || $\sum _ { k _ { 1 } , \ldots , k _ { n } = 0 } ^ { \infty } c _ { k _ { 1 } \cdots k _ { n } } ( z _ { 1 } - \zeta _ { 1 } ) ^ { k _ { 1 } } \ldots ( z _ { n } - \zeta _ { n } ) ^ { k _ { n } }$ | ||
| + | ||$$\sum _ {k_1,\ldots ,k_n=0}^{\infty }c_{k_1\cdots k _ n}(z_1-\zeta _ 1)^{k_1}\ldots (z_n-\zeta _ n)^{k_n}$$ | ||
| + | || conf 0.324 | ||
s085590225.png (225) | s085590225.png (225) | ||
|- | |- | ||
| − | | 110.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|46.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590404.png || $\frac { m _ { 1 } } { n _ { 1 } } < \frac { m _ { 2 } } { n _ { 1 } n _ { 2 } } < \ldots < \frac { m _ { g } } { n _ { 1 } \ldots n _ { g } } = \frac { m _ { g } } { n }$ || $$ \frac { | + | | 110.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|46.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590404.png | ||
| + | || $\frac { m _ { 1 } } { n _ { 1 } } < \frac { m _ { 2 } } { n _ { 1 } n _ { 2 } } < \ldots < \frac { m _ { g } } { n _ { 1 } \ldots n _ { g } } = \frac { m _ { g } } { n }$ | ||
| + | ||$$\frac {m_1}{n_1}<\frac {m_2}{n_1n_2}<\ldots <\frac {m_g}{n_1\ldots n _ g}=\frac {m_g}n$$ | ||
| + | || conf 0.459 | ||
s085590404.png (404) | s085590404.png (404) | ||
|- | |- | ||
| − | | 111.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|115.]])*|| https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590429.png || $p ( Z ) = 1 - \operatorname { dim } H ^ { 0 } ( Z , O _ { Z } ) + \operatorname { dim } H ^ { 1 } ( Z , O _ { Z } )$ || $$ p ( Z ) = 1 - \operatorname { dim } H ^ | + | | 111.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|115.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590429.png | ||
| + | || $p ( Z ) = 1 - \operatorname { dim } H ^ { 0 } ( Z , O _ { Z } ) + \operatorname { dim } H ^ { 1 } ( Z , O _ { Z } )$ | ||
| + | ||$$p(Z)=1-\operatorname {dim}H^0({\mathbf Z},{\cal O}_{\mathbf Z })+\operatorname {dim}H^1({\mathbf Z},{\cal O}_{\mathbf Z })$$ | ||
| + | || conf 0.997 F | ||
s085590429.png (429) | s085590429.png (429) | ||
|- | |- | ||
| − | | 112.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|136.]])*|| https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590440.png || $X _ { \epsilon } = \{ ( x _ { 0 } , \ldots , x _ { x } ) : f ( x _ { 0 } , \ldots , x _ { x } ) = \epsilon \}$ || $$ | + | | 112.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|136.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590440.png | ||
| + | || $X _ { \epsilon } = \{ ( x _ { 0 } , \ldots , x _ { x } ) : f ( x _ { 0 } , \ldots , x _ { x } ) = \epsilon \}$ | ||
| + | ||$$X_{\epsilon }=\{(x_0,\ldots ,x_x):f(x_0,\ldots ,x_x)=\epsilon \}$$ | ||
| + | || conf 0.433 F | ||
s085590440.png (440) | s085590440.png (440) | ||
|- | |- | ||
| − | | 113.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|12.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590458.png || $= \left\{ \begin{array} { l l } { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } } & { \text { if } \mu = 2 k } \\ { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } ( x + ( k + 1 ) \lambda ) } & { \text { if } \mu = 2 k + 1 } \end{array} \right.$ || $$ = \left\{ \begin{array} { | + | | 113.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|12.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590458.png | ||
| + | || $= \left\{ \begin{array} { l l } { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } } & { \text { if } \mu = 2 k } \\ { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } ( x + ( k + 1 ) \lambda ) } & { \text { if } \mu = 2 k + 1 } \end{array} \right.$ | ||
| + | ||$$=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | {(x+\lambda )^2\ldots (x+k\lambda )^2} &{\text{ if }\mu =2k,}\\ | ||
| + | {(x+\lambda )^2\ldots (x+k\lambda )^2(x+(k+1)\lambda )} &{\text{ if }\mu =2k+1,} | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.870 | ||
s085590458.png (458) | s085590458.png (458) | ||
|- | |- | ||
| − | | 114.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|75.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590482.png || $( \frac { \partial F ( x , y , \lambda ) } { \partial x } , \frac { \partial F ( x , y , \lambda ) } { \partial y } )$ || $$ \big( \frac { \partial F ( x , y , \lambda ) } { \partial x } , \frac { \partial F ( x , y , \lambda ) } { \partial y } \big) $$|| conf 0.986 | + | | 114.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|75.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590482.png | ||
| + | || $( \frac { \partial F ( x , y , \lambda ) } { \partial x } , \frac { \partial F ( x , y , \lambda ) } { \partial y } )$ | ||
| + | ||$$\big(\frac {\partial F (x,y,\lambda )}{\partial x },\frac {\partial F (x,y,\lambda )}{\partial y }\big)$$ | ||
| + | || conf 0.986 | ||
s085590482.png (482) | s085590482.png (482) | ||
|- | |- | ||
| − | | 115.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|137.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590515.png || $\frac { d x _ { i } } { d x _ { i _ { 0 } } } = f _ { i } ( x ) , \quad f _ { i } \in C ( U ) , \quad i \neq i _ { 0 }$ || $$ \frac { | + | | 115.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|137.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590515.png | ||
| + | || $\frac { d x _ { i } } { d x _ { i _ { 0 } } } = f _ { i } ( x ) , \quad f _ { i } \in C ( U ) , \quad i \neq i _ { 0 }$ | ||
| + | ||$$\frac {dx_i}{dx_{i_0}}=f_i(x),\quad f _ i\in C (U),\quad i \neq i _ 0.$$ | ||
| + | || conf 0.594 | ||
s085590515.png (515) | s085590515.png (515) | ||
|- | |- | ||
| − | | 116.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|142.]])*|| https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590527.png || $A = \| \left. \begin{array} { l l } { \alpha } & { b } \\ { c } & { e } \end{array} \right. |$ || $$ A = | + | | 116.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|142.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590527.png | ||
| + | || $A = \| \left. \begin{array} { l l } { \alpha } & { b } \\ { c } & { e } \end{array} \right. |$ | ||
| + | ||$$A=\left\| | ||
| + | \begin {array}{ll} | ||
| + | {\alpha } &b\\ | ||
| + | c &e | ||
| + | \end {array} | ||
| + | \right\|$$ | ||
| + | || conf 0.506 F | ||
s085590527.png (527) | s085590527.png (527) | ||
|- | |- | ||
| − | | 117.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|53.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590634.png || $\Delta = ( F _ { x x } ^ { \prime \prime } ) _ { 0 } ( F _ { y y } ^ { \prime \prime } ) _ { 0 } - ( F _ { x y } ^ { \prime \prime } ) _ { 0 } ^ { 2 }$ || $$ \Delta = ( | + | | 117.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|53.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590634.png | ||
| + | || $\Delta = ( F _ { x x } ^ { \prime \prime } ) _ { 0 } ( F _ { y y } ^ { \prime \prime } ) _ { 0 } - ( F _ { x y } ^ { \prime \prime } ) _ { 0 } ^ { 2 }$ | ||
| + | ||$$\Delta =(F_{xx}^{\prime \prime })_0(F_{yy}^{\prime \prime })_0-(F_{xy}^{\prime \prime })_0^2$$ | ||
| + | || conf 0.920 | ||
s085590634.png (634) | s085590634.png (634) | ||
|- | |- | ||
| − | | 118.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|16.]])*|| https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590645.png || $\left| \begin{array} { l l l } { F _ { X } ^ { \prime } } & { F _ { y } ^ { \prime } } & { F _ { z } ^ { \prime } } \\ { G _ { \chi } ^ { \prime } } & { G _ { y } ^ { \prime } } & { G _ { Z } ^ { \prime } } \end{array} \right|$ || $$ \left\| \begin{array} { | + | | 118.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|16.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590645.png | ||
| + | || $\left| \begin{array} { l l l } { F _ { X } ^ { \prime } } & { F _ { y } ^ { \prime } } & { F _ { z } ^ { \prime } } \\ { G _ { \chi } ^ { \prime } } & { G _ { y } ^ { \prime } } & { G _ { Z } ^ { \prime } } \end{array} \right|$ | ||
| + | ||$$\left\| | ||
| + | \begin {array}{lll} | ||
| + | {F_x^{\prime }} &{F_y^{\prime }} &{F_z^{\prime }}\\ | ||
| + | {G_x^{\prime }} &{G_y^{\prime }} &{G_Z^{\prime }} | ||
| + | \end {array} | ||
| + | \right\|$$ | ||
| + | || conf 0.230 F | ||
s085590645.png (645) | s085590645.png (645) | ||
|- | |- | ||
| − | | 119.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|92.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590653.png || $( F _ { X } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { y } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { z } ^ { \prime } ) _ { 0 } = 0$ || $$ ( | + | | 119.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|92.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s085/s085590/s085590653.png | ||
| + | || $( F _ { X } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { y } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { z } ^ { \prime } ) _ { 0 } = 0$ | ||
| + | ||$$(F_x^{\prime })_0=0,\quad (F_y^{\prime })_0=0,\quad (F_z^{\prime })_0=0.$$ | ||
| + | || conf 0.300 | ||
s085590653.png (653) | s085590653.png (653) | ||
| Line 904: | Line 1,571: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 120.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|138.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s086/s086100/s08610054.png || $\{ e \} \rightarrow \Delta \rightarrow \pi \rightarrow Z ^ { s } \rightarrow \{ e \}$ || $$ \{ e \} \rightarrow \Delta \rightarrow \pi \rightarrow {\mathbf Z} ^ | + | | 120.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|138.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s086/s086100/s08610054.png | ||
| + | || $\{ e \} \rightarrow \Delta \rightarrow \pi \rightarrow Z ^ { s } \rightarrow \{ e \}$ | ||
| + | ||$$\{e\}\rightarrow \Delta \rightarrow \pi \rightarrow {\mathbf Z}^s\rightarrow \{e\}$$ | ||
| + | || conf 0.972 | ||
s08610054.png (54) | s08610054.png (54) | ||
| Line 918: | Line 1,589: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 121.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|71.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706033.png || $\psi _ { t _ { 1 } , \ldots , t _ { R } } ^ { \prime } : S K _ { 1 } ( R ) \rightarrow S K _ { 1 } ( R ( t _ { 1 } , \ldots , t _ { n } ) )$ || $$ \psi _ { | + | | 121.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|71.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s087/s087060/s08706033.png | ||
| + | || $\psi _ { t _ { 1 } , \ldots , t _ { R } } ^ { \prime } : S K _ { 1 } ( R ) \rightarrow S K _ { 1 } ( R ( t _ { 1 } , \ldots , t _ { n } ) )$ | ||
| + | ||$$\psi _ {t_1,\ldots ,t_n}^{\prime }:SK_1(R)\rightarrow S K _ 1(R(t_1,\ldots ,t_n)).$$ | ||
| + | || conf 0.379 | ||
s08706033.png (33) | s08706033.png (33) | ||
| Line 932: | Line 1,607: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 122.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|130.]]) || https://www.encyclopediaofmath.org/legacyimages/s/s130/s130530/s13053016.png || $e = \frac { | U | } { | G | } ( \sum _ { b \in B } b ) ( \sum _ { w \in W } \operatorname { sign } ( w ) w )$ || $$ e = \frac { | U | } { | G | } \big( \sum _ { b \in B } b \big) \big( \sum _ { w \in W } \operatorname { sign } ( w ) w \big) $$|| conf 0.138 | + | | 122.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|130.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s130/s130530/s13053016.png | ||
| + | || $e = \frac { | U | } { | G | } ( \sum _ { b \in B } b ) ( \sum _ { w \in W } \operatorname { sign } ( w ) w )$ | ||
| + | ||$$e=\frac {|U|}{|G|}\big(\sum _ {b\in B }b\big)\big(\sum _ {w\in W }\operatorname {sign}(w)w\big)$$ | ||
| + | || conf 0.138 | ||
s13053016.png (16) | s13053016.png (16) | ||
| Line 946: | Line 1,625: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 123.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|24.]])*|| https://www.encyclopediaofmath.org/legacyimages/s/s130/s130540/s13054017.png || $( x _ { i j } ( a ) , x _ { k l } ( b ) ) = \left\{ \begin{array} { l l } { 1 } & { \text { if } i \neq 1 , j \neq k } \\ { x _ { 1 } ( a b ) } & { \text { if } i \neq 1 , j = k } \end{array} \right.$ || $$ ( | + | | 123.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|24.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/s/s130/s130540/s13054017.png | ||
| + | || $( x _ { i j } ( a ) , x _ { k l } ( b ) ) = \left\{ \begin{array} { l l } { 1 } & { \text { if } i \neq 1 , j \neq k } \\ { x _ { 1 } ( a b ) } & { \text { if } i \neq 1 , j = k } \end{array} \right.$ | ||
| + | ||$$(x_{ij}(a),x_{kl}(b))=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | 1 &{\text{ if }i\neq l ,j\neq k },\\ | ||
| + | {x_{il}(ab)} &{\text{ if }i\neq l ,j=k}. | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.381 F | ||
s13054017.png (17) | s13054017.png (17) | ||
|- | |- | ||
|} | |} | ||
| + | |||
==[[Tilting theory]]== | ==[[Tilting theory]]== | ||
{| class="wikitable" style="text-align: left; width: 1740px;" | {| class="wikitable" style="text-align: left; width: 1740px;" | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 124.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|84.]]) || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130130/t130130105.png || $0 \rightarrow \Lambda \rightarrow T _ { 1 } \rightarrow \ldots \rightarrow T _ { n } \rightarrow 0$ || $$ 0 \rightarrow \Lambda \rightarrow T _ | + | | 124.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|84.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130130/t130130105.png | ||
| + | || $0 \rightarrow \Lambda \rightarrow T _ { 1 } \rightarrow \ldots \rightarrow T _ { n } \rightarrow 0$ | ||
| + | ||$$0\rightarrow \Lambda \rightarrow T _ 1\rightarrow \ldots \rightarrow T _ n\rightarrow 0 $$ | ||
| + | || conf 0.946 | ||
t130130105.png (105) | t130130105.png (105) | ||
| Line 974: | Line 1,667: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 125.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|18.]]) || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140104.png || $q R ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { i } x _ { j } + \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { , j } x _ { i } x _ { j }$ || $$ q_R ( x ) = \sum _ { j \in Q _ | + | | 125.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|18.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140104.png | ||
| + | || $q R ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { i } x _ { j } + \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { , j } x _ { i } x _ { j }$ | ||
| + | ||$$q_R(x)=\sum _ {j\in Q _ 0}x_j^2-\sum _ {\langle \beta :i\rightarrow j )\in Q _ 1}x_ix_j+\sum _ {\langle \beta :i\rightarrow j )\in Q _ 1}r_{i,j}x_ix_j,$$ | ||
| + | || conf 0.112 | ||
t130140104.png (104) | t130140104.png (104) | ||
|- | |- | ||
| − | | 126.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|40.]]) || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140118.png || $[ X ] \mapsto \chi _ { R } ( [ X ] ) = \sum _ { m = 0 } ^ { \infty } ( - 1 ) ^ { m } \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { m } ( X , X )$ || $$ [ X ] \mapsto \chi _ | + | | 126.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|40.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140118.png | ||
| + | || $[ X ] \mapsto \chi _ { R } ( [ X ] ) = \sum _ { m = 0 } ^ { \infty } ( - 1 ) ^ { m } \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { m } ( X , X )$ | ||
| + | ||$$[X]\mapsto \chi _ R([X])=\sum _ {m=0}^{\infty }(-1)^m\operatorname {dim}_K\operatorname {Ext}_R^m(X,X)$$ | ||
| + | || conf 0.116 | ||
t130140118.png (118) | t130140118.png (118) | ||
|- | |- | ||
| − | | 127.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|132.]])*|| https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140119.png || $\operatorname { dim } _ { 1 } : K _ { 0 } ( \operatorname { mod } R ) \rightarrow Z ^ { Q _ { 0 } }$ || $$ \ | + | | 127.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|132.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140119.png | ||
| + | || $\operatorname { dim } _ { 1 } : K _ { 0 } ( \operatorname { mod } R ) \rightarrow Z ^ { Q _ { 0 } }$ | ||
| + | ||$$\underline {\dim }:K_0(\operatorname {mod}R)\rightarrow {\mathbf Z}^{Q_0}$$ | ||
| + | || conf 0.287 F | ||
t130140119.png (119) | t130140119.png (119) | ||
|- | |- | ||
| − | | 128.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|37.]])*|| https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140140.png || $q ( x ) = \sum _ { i \in I } x _ { i } ^ { 2 } + \sum _ { i \prec j } x _ { i } x _ { j } - \sum _ { p \in \operatorname { max } l } ( \sum _ { i \prec p } x _ { i } ) x _ { p }$ || $$ q_I ( x ) = \sum _ { i \in I } | + | | 128.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|37.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t130140140.png | ||
| + | || $q ( x ) = \sum _ { i \in I } x _ { i } ^ { 2 } + \sum _ { i \prec j } x _ { i } x _ { j } - \sum _ { p \in \operatorname { max } l } ( \sum _ { i \prec p } x _ { i } ) x _ { p }$ | ||
| + | ||$$q_I(x)=\sum _ {i\in I }x_i^2+\sum _ {i\prec j \atop j\in I\setminus {\rm max}I}x_ix_j-\sum _ {p\in \operatorname {max}I}\big(\sum _ {i\prec p }x_i\big)x_p$$ | ||
| + | || conf 0.197 F | ||
t130140140.png (140) | t130140140.png (140) | ||
|- | |- | ||
| − | | 129.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|131.]])*|| https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t13014044.png || $X \mapsto \operatorname { dim } X = ( \operatorname { dim } _ { K } X _ { j } ) _ { j \in Q _ { 0 } }$ || $$ X \mapsto \ | + | | 129.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|131.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t13014044.png | ||
| + | || $X \mapsto \operatorname { dim } X = ( \operatorname { dim } _ { K } X _ { j } ) _ { j \in Q _ { 0 } }$ | ||
| + | ||$$X\mapsto \underline {\dim }X=(\operatorname {dim}_KX_j)_{j\in Q _ 0}$$ | ||
| + | || conf 0.819 F | ||
t13014044.png (44) | t13014044.png (44) | ||
|- | |- | ||
| − | | 130.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|25.]] | + | | 130.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|25.]] |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t13014048.png | ||
| + | || $[ X ] \mapsto \chi _ { Q } ( [ X ] ) = \operatorname { dim } _ { K } \operatorname { End } _ { Q } ( X ) - \operatorname { dim } _ { K } \operatorname { Ext } _ { Q } ^ { 1 } ( X , X )$ | ||
| + | ||$$[X]\mapsto \chi _ Q([X])=\operatorname {dim}_K\operatorname {End}_Q(X)-\operatorname {dim}_K\operatorname {Ext}_Q^1(X,X)$$ | ||
| + | || conf 0.661 | ||
t13014048.png (48) | t13014048.png (48) | ||
|- | |- | ||
| − | | 131.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|38.]])*|| https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t13014056.png || $A _ { Q } ( v ) = \prod _ { i , j \in Q _ { 0 } } \prod _ { \langle \beta : j \rightarrow i \rangle \in Q _ { 1 } } M _ { v _ { i } \times v _ { j } } ( K ) _ { \beta }$ || $$ | + | | 131.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|38.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t13014056.png | ||
| + | || $A _ { Q } ( v ) = \prod _ { i , j \in Q _ { 0 } } \prod _ { \langle \beta : j \rightarrow i \rangle \in Q _ { 1 } } M _ { v _ { i } \times v _ { j } } ( K ) _ { \beta }$ | ||
| + | ||$$A_Q(v)=\prod _ {i,j\in Q _ 0}\prod _ {\langle \beta :j\rightarrow i \rangle \in Q _ 1}M_{v_i\times v _ j}(K)_{\beta }$$ | ||
| + | || conf 0.481 F | ||
t13014056.png (56) | t13014056.png (56) | ||
|- | |- | ||
| − | | 132.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|139.]])*|| https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t1301406.png || $\Phi ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { i , j \in Q _ { 0 } } d _ { i j } x _ { i } x _ { j }$ || $$ q_Q ( x ) = \sum _ { j \in Q _ | + | | 132.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|139.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t130/t130140/t1301406.png | ||
| + | || $\Phi ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { i , j \in Q _ { 0 } } d _ { i j } x _ { i } x _ { j }$ | ||
| + | ||$$q_Q(x)=\sum _ {j\in Q _ 0}x_j^2-\sum _ {i,j\in Q _ 0}d_{ij}x_ix_j,$$ | ||
| + | || conf 0.648 F | ||
t1301406.png (6) | t1301406.png (6) | ||
|- | |- | ||
|} | |} | ||
| + | |||
==[[Torus]]== | ==[[Torus]]== | ||
{| class="wikitable" style="text-align: left; width: 1740px;" | {| class="wikitable" style="text-align: left; width: 1740px;" | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 133.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|41.]])*|| https://www.encyclopediaofmath.org/legacyimages/t/t093/t093350/t0933502.png || $r = \alpha \operatorname { sin } u k + l ( 1 + \epsilon \operatorname { cos } u ) ( i \operatorname { cos } v + j \operatorname { sin } v )$ || $$ r = \alpha \operatorname { sin } u {\bf k} + l ( 1 + \epsilon \operatorname { cos } u ) ( {\bf i} \operatorname { cos } v + {\bf j} \operatorname { sin } v ) $$|| conf 0.585 F | + | | 133.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|41.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t093/t093350/t0933502.png | ||
| + | || $r = \alpha \operatorname { sin } u k + l ( 1 + \epsilon \operatorname { cos } u ) ( i \operatorname { cos } v + j \operatorname { sin } v )$ | ||
| + | ||$$r=\alpha \operatorname {sin}u{\bf k}+l(1+\epsilon \operatorname {cos}u)({\bf i}\operatorname {cos}v+{\bf j}\operatorname {sin}v)$$ | ||
| + | || conf 0.585 F | ||
t0933502.png (2) | t0933502.png (2) | ||
|- | |- | ||
| − | | 134.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|122.]])*|| https://www.encyclopediaofmath.org/legacyimages/t/t093/t093350/t0933507.png || $d s ^ { 2 } = \alpha ^ { 2 } d u ^ { 2 } + l ^ { 2 } ( 1 + \epsilon \operatorname { cos } u ) ^ { 2 } d v ^ { 2 }$ || $$ | + | | 134.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|122.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/t/t093/t093350/t0933507.png | ||
| + | || $d s ^ { 2 } = \alpha ^ { 2 } d u ^ { 2 } + l ^ { 2 } ( 1 + \epsilon \operatorname { cos } u ) ^ { 2 } d v ^ { 2 }$ | ||
| + | ||$$ds^2=\alpha ^2du^2+l^2(1+\epsilon \operatorname {cos}u)^2dv^2,$$ | ||
| + | || conf 0.696 F | ||
t0933507.png (7) | t0933507.png (7) | ||
| Line 1,034: | Line 1,768: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 135.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|9.]]) || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524027.png || $u _ { 3 } ( x ) = \left\{ \begin{array} { l l } { \frac { x ^ { 2 } } { 2 } , } & { 0 \leq x < 1 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } ] } { 2 } , } & { 1 \leq x < 2 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } + 3 ( x - 2 ) ^ { 2 } ] } { 2 } , } & { 2 \leq x < 3 } \\ { 0 , } & { x \notin [ 0,3 ] } \end{array} \right.$ || $$ | + | | 135.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|9.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524027.png | ||
| + | || $u _ { 3 } ( x ) = \left\{ \begin{array} { l l } { \frac { x ^ { 2 } } { 2 } , } & { 0 \leq x < 1 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } ] } { 2 } , } & { 1 \leq x < 2 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } + 3 ( x - 2 ) ^ { 2 } ] } { 2 } , } & { 2 \leq x < 3 } \\ { 0 , } & { x \notin [ 0,3 ] } \end{array} \right.$ | ||
| + | ||$$u_3(x)=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | {\frac {x^2}2,} &{0\leq x <1,}\\ | ||
| + | {\frac {[x^2-3(x-1)^2]}2,} &{1\leq x <2,}\\ | ||
| + | {\frac {[x^2-3(x-1)^2+3(x-2)^2]}2,} &{2\leq x <3,}\\ | ||
| + | {0,} &{x\notin [0,3].} | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.733 | ||
u09524027.png (27) | u09524027.png (27) | ||
|- | |- | ||
| − | | 136.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|32.]])*|| https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u0952403.png || $p ( x ) = \left\{ \begin{array} { l l } { \frac { 1 } { b - \alpha } , } & { x \in [ \alpha , b ] } \\ { 0 , } & { x \notin [ \alpha , b ] } \end{array} \right.$ || $$ p ( x ) = \left\{ \begin{array} { | + | | 136.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|32.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u0952403.png | ||
| + | || $p ( x ) = \left\{ \begin{array} { l l } { \frac { 1 } { b - \alpha } , } & { x \in [ \alpha , b ] } \\ { 0 , } & { x \notin [ \alpha , b ] } \end{array} \right.$ | ||
| + | ||$$p(x)=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | {\frac 1{b-\alpha },} &{x\in [\alpha ,b],}\\ | ||
| + | {0,} &{x\notin [\alpha ,b].} | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.681 F | ||
u0952403.png (3) | u0952403.png (3) | ||
|- | |- | ||
| − | | 137.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|34.]]) || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524030.png || $u _ { n } ( x ) = \frac { 1 } { ( n - 1 ) ! } \sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) ( x - k ) _ { + } ^ { n - 1 }$ || $$ | + | | 137.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|34.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524030.png | ||
| + | || $u _ { n } ( x ) = \frac { 1 } { ( n - 1 ) ! } \sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) ( x - k ) _ { + } ^ { n - 1 }$ | ||
| + | ||$$u_n(x)=\frac 1{(n-1)!}\sum _ {k=0}^n(-1)^k\left(\begin {array}ln\\ | ||
| + | k | ||
| + | \end {array} | ||
| + | \right)(x-k)_{+}^{n-1}$$ | ||
| + | || conf 0.569 | ||
u09524030.png (30) | u09524030.png (30) | ||
|- | |- | ||
| − | | 138.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|109.]]) || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524034.png || $z _ { + } = \left\{ \begin{array} { l l } { z , } & { z > 0 } \\ { 0 , } & { z \leq 0 } \end{array} \right.$ || $$ | + | | 138.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|109.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524034.png | ||
| + | || $z _ { + } = \left\{ \begin{array} { l l } { z , } & { z > 0 } \\ { 0 , } & { z \leq 0 } \end{array} \right.$ | ||
| + | ||$$z_{+}=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | {z,} &{z>0}.\\ | ||
| + | {0,} &{z\leq 0 }. | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.676 | ||
u09524034.png (34) | u09524034.png (34) | ||
|- | |- | ||
| − | | 139.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|43.]]) || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u0952407.png || $F ( x ) = \left\{ \begin{array} { l l } { 0 , } & { x \leq a } \\ { \frac { x - a } { b - a } , } & { a < x \leq b } \\ { 1 , } & { x > b } \end{array} \right.$ || $$ F ( x ) = \left\{ \begin{array} { | + | | 139.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|43.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u0952407.png | ||
| + | || $F ( x ) = \left\{ \begin{array} { l l } { 0 , } & { x \leq a } \\ { \frac { x - a } { b - a } , } & { a < x \leq b } \\ { 1 , } & { x > b } \end{array} \right.$ | ||
| + | ||$$F(x)=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | {0,} &{x\leq a },\\ | ||
| + | {\frac {x-a}{b-a},} &{a<x\leq b },\\ | ||
| + | {1,} &{x>b}, | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.468 | ||
u0952407.png (7) | u0952407.png (7) | ||
|- | |- | ||
| − | | 140.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|47.]]) || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524072.png || $p ( x _ { 1 } , \ldots , x _ { n } ) = \left\{ \begin{array} { l l } { C \neq 0 , } & { x \in D } \\ { 0 , } & { x \notin D } \end{array} \right.$ || $$ p ( | + | | 140.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|47.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095240/u09524072.png | ||
| + | || $p ( x _ { 1 } , \ldots , x _ { n } ) = \left\{ \begin{array} { l l } { C \neq 0 , } & { x \in D } \\ { 0 , } & { x \notin D } \end{array} \right.$ | ||
| + | ||$$p(x_1,\ldots ,x_n)=\left\{ | ||
| + | \begin {array}{ll} | ||
| + | {C\neq 0 ,} &{x\in D },\\ | ||
| + | {0,} &{x\notin D }, | ||
| + | \end {array} | ||
| + | \right.$$ | ||
| + | || conf 0.705 | ||
u09524072.png (72) | u09524072.png (72) | ||
| Line 1,068: | Line 1,857: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 141.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|143.]]) || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095410/u0954106.png || $\{ g \in \operatorname { GL } ( V ) : ( 1 - g ) ^ { n } = 0 \} , \quad n = \operatorname { dim } V$ || $$ \{ g \in \operatorname { GL } ( V ) : ( 1 - g ) ^ | + | | 141.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|143.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/u/u095/u095410/u0954106.png | ||
| + | || $\{ g \in \operatorname { GL } ( V ) : ( 1 - g ) ^ { n } = 0 \} , \quad n = \operatorname { dim } V$ | ||
| + | ||$$\{g\in \operatorname {GL}(V):(1-g)^n=0\},\quad n =\operatorname {dim}V,$$ | ||
| + | || conf 0.287 | ||
u0954106.png (6) | u0954106.png (6) | ||
| Line 1,082: | Line 1,875: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 142.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|51.]]) || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090122.png || $\operatorname { diag } ( t _ { 1 } , \ldots , t _ { n } ) \mapsto t _ { 1 } ^ { \lambda _ { 1 } } \ldots t _ { n } ^ { \lambda _ { n } } \in K$ || $$ \operatorname { diag } ( | + | | 142.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|51.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090122.png | ||
| + | || $\operatorname { diag } ( t _ { 1 } , \ldots , t _ { n } ) \mapsto t _ { 1 } ^ { \lambda _ { 1 } } \ldots t _ { n } ^ { \lambda _ { n } } \in K$ | ||
| + | ||$$\operatorname {diag}(t_1,\ldots ,t_n)\mapsto t _ 1^{\lambda _ 1}\ldots t _ n^{\lambda _ n}\in K,$$ | ||
| + | || conf 0.507 | ||
w120090122.png (122) | w120090122.png (122) | ||
|- | |- | ||
| − | | 143.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|54.]])*|| https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090135.png || $\chi _ { \lambda } = \sum _ { \mu \in \Lambda ( n ) } \operatorname { dim } _ { K } ( \Delta ( \lambda ) ^ { \mu } ) _ { e _ { \mu } }$ || $$ \chi _ { \lambda } = \sum _ { \mu \in \Lambda ( n ) } \operatorname { dim } | + | | 143.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|54.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090135.png | ||
| + | || $\chi _ { \lambda } = \sum _ { \mu \in \Lambda ( n ) } \operatorname { dim } _ { K } ( \Delta ( \lambda ) ^ { \mu } ) _ { e _ { \mu } }$ | ||
| + | ||$$\chi _ {\lambda }=\sum _ {\mu \in \Lambda (n)}\operatorname {dim}_K(\Delta (\lambda )^{\mu })_{e_{\mu }},$$ | ||
| + | || conf 0.461 F | ||
w120090135.png (135) | w120090135.png (135) | ||
|- | |- | ||
| − | | 144.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|110.]]) || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090259.png || $\mathfrak { B } = \{ e _ { \pm } \alpha , h _ { \beta } : \alpha \in \Phi ^ { + } , \beta \in \Sigma \}$ || $$ \mathfrak | + | | 144.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|110.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090259.png | ||
| + | || $\mathfrak { B } = \{ e _ { \pm } \alpha , h _ { \beta } : \alpha \in \Phi ^ { + } , \beta \in \Sigma \}$ | ||
| + | ||$$\mathfrak B=\{e_{\pm }\alpha ,h_{\beta }:\alpha \in \Phi ^{+},\beta \in \Sigma \}.$$ | ||
| + | || conf 0.381 | ||
w120090259.png (259) | w120090259.png (259) | ||
|- | |- | ||
| − | | 145.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|82.]]) || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090342.png || $\left( \begin{array} { c } { h } \\ { i } \end{array} \right) = \frac { h ( h - 1 ) \ldots ( h - i + 1 ) } { i ! }$ || $$ \left( \begin{array} | + | | 145.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|82.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w120090342.png | ||
| + | || $\left( \begin{array} { c } { h } \\ { i } \end{array} \right) = \frac { h ( h - 1 ) \ldots ( h - i + 1 ) } { i ! }$ | ||
| + | ||$$\left( | ||
| + | \begin {array}ch\\ | ||
| + | i | ||
| + | \end {array} | ||
| + | \right)=\frac {h(h-1)\ldots (h-i+1)}{i!} | ||
| + | $$ | ||
| + | || conf 0.487 | ||
w120090342.png (342) | w120090342.png (342) | ||
|- | |- | ||
| − | | 146.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|28.]])*|| https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w12009095.png || $\mathfrak { S } _ { \{ 1 , \ldots , \lambda _ { 1 } \} } \times \mathfrak { S } _ { \{ \lambda _ { 1 } + 1 , \ldots , \lambda _ { 1 } + \lambda _ { 2 } \} } \times$ || $$ \mathfrak | + | | 146.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|28.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w12009095.png | ||
| + | || $\mathfrak { S } _ { \{ 1 , \ldots , \lambda _ { 1 } \} } \times \mathfrak { S } _ { \{ \lambda _ { 1 } + 1 , \ldots , \lambda _ { 1 } + \lambda _ { 2 } \} } \times$ | ||
| + | ||$$\mathfrak S_{\{1,\ldots ,\lambda _ 1\}}\times \mathfrak S_{\{\lambda _ 1+1,\ldots ,\lambda _ 1+\lambda _ 2\}}\times \dots $$ | ||
| + | || conf 0.312 F | ||
w12009095.png (95) | w12009095.png (95) | ||
|- | |- | ||
| − | | 147.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|104.]]) || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w12009096.png || $\ldots \times \mathfrak { S } _ { \{ \lambda _ { 1 } + \ldots + \lambda _ { n - 1 } + 1 , \ldots , r \} }$ || $$ \ldots \times \mathfrak | + | | 147.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|104.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w120/w120090/w12009096.png | ||
| + | || $\ldots \times \mathfrak { S } _ { \{ \lambda _ { 1 } + \ldots + \lambda _ { n - 1 } + 1 , \ldots , r \} }$ | ||
| + | ||$$\ldots \times \mathfrak S_{\{\lambda _ 1+\ldots +\lambda _ {n-1}+1,\ldots ,r\}},$$ | ||
| + | || conf 0.259 | ||
w12009096.png (96) | w12009096.png (96) | ||
| Line 1,116: | Line 1,938: | ||
!style=width: 3%| Nr. | !style=width: 3%| Nr. | ||
!style=width: 30%| Image of png File | !style=width: 30%| Image of png File | ||
| − | !style=width: 30%| $\TeX$, | + | !style=width: 30%| $\TeX$, automatically generated version |
| − | !style=width: 30%| $\TeX$, corrected version | + | !style=width: 30%| $\TeX$, manually corrected version |
!style=width: 7%| Confidence, F? | !style=width: 7%| Confidence, F? | ||
png file | png file | ||
|- | |- | ||
| − | | 148.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|87.]])*|| https://www.encyclopediaofmath.org/legacyimages/w/w098/w098100/w098100172.png || $\langle \alpha > < b \rangle = \langle \alpha b \rangle , \quad \langle 1 \rangle = f _ { 1 } = V _ { 1 } =$ || $$ \langle \alpha > < b \rangle = \langle \alpha b \rangle , \quad \langle {\bf 1} \rangle = {\bf f} | + | | 148.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|87.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w098/w098100/w098100172.png | ||
| + | || $\langle \alpha > < b \rangle = \langle \alpha b \rangle , \quad \langle 1 \rangle = f _ { 1 } = V _ { 1 } =$ | ||
| + | ||$$\langle \alpha ><b\rangle =\langle \alpha b \rangle ,\quad \langle {\bf 1}\rangle ={\bf f}_1={\bf V}_1=\text{ unit element}1,$$ | ||
| + | || conf 0.351 F | ||
w098100172.png (172) | w098100172.png (172) | ||
|- | |- | ||
| − | | 149.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|123.]])*|| https://www.encyclopediaofmath.org/legacyimages/w/w098/w098100/w098100177.png || $\langle \alpha + b \rangle = \sum _ { n = 1 } ^ { \infty } V _ { n } \langle r _ { n } ( \alpha , b ) f$ || $$ \langle \alpha + b \rangle = \sum _ { n = 1 } ^ { \infty } {\bf V} | + | | 149.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|123.]])* |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w098/w098100/w098100177.png | ||
| + | || $\langle \alpha + b \rangle = \sum _ { n = 1 } ^ { \infty } V _ { n } \langle r _ { n } ( \alpha , b ) f$ | ||
| + | ||$$\langle \alpha +b\rangle =\sum _ {n=1}^{\infty }{\bf V}_n\langle r _ n(\alpha ,b){\bf f}_n.$$ | ||
| + | || conf 0.143 F | ||
w098100177.png (177) | w098100177.png (177) | ||
|- | |- | ||
| − | | 150.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|102.]]) || https://www.encyclopediaofmath.org/legacyimages/w/w098/w098100/w098100190.png || $\sigma ( \alpha _ { 1 } , \alpha _ { 2 } , \ldots ) = ( \alpha _ { 1 } ^ { p } , \alpha _ { 2 } ^ { p } , \ldots )$ || $$ \sigma ( \alpha _ | + | | 150.([[User:Maximilian Janisch/latexlist/latex/Algebraic Groups/E|102.]]) |
| + | || https://www.encyclopediaofmath.org/legacyimages/w/w098/w098100/w098100190.png | ||
| + | || $\sigma ( \alpha _ { 1 } , \alpha _ { 2 } , \ldots ) = ( \alpha _ { 1 } ^ { p } , \alpha _ { 2 } ^ { p } , \ldots )$ | ||
| + | ||$$\sigma (\alpha _ 1,\alpha _ 2,\ldots )=(\alpha _ 1^p,\alpha _ 2^p,\ldots )$$ | ||
| + | || conf 0.771 | ||
w098100190.png (190) | w098100190.png (190) | ||
|- | |- | ||
|} | |} | ||
Latest revision as of 17:27, 11 November 2019
This page gives an analysis of the code here, generated automatically from some png files underlying our old wiki pages. As this page does contain a lot of $\TeX$ code, it loads slowly.
Under the name of some of our EoM-pages the table below lists some png files, displaying their image and their $TeX$ rendering (automatically retrieved and corrected by hand). The first column gives the running number in this table, followed (in parentheses) by the number used here. The last column gives the confidence and the name of the png file, followed (in parentheses) by the number it has in the sequence of all png files called by its calling EoM-page.
Here is a short survey of the more systematic errors which seem to occur:
- 1. Trailing punctuation is dismissed.
- [concerns almost all images] ; technically: pixels in sparse last pixel columns of bit images are suppressed/ignored?
- 2. "Displayed" images are not recognized as such.
- [concerns almost all images]
- Therefore these are displayed too small, and like "inline" $\TeX$ format.
- Remark: This cannot be discovered from the png file, it has to be retrieved from the html markup in the calling file: Displayed images are embedded in some html <table> markup.
- 3. Sparse initial column pixels of the bit image are dismissed
- (in parts this affects essential symbols), [see nr. 15,16,36,43,58,59,60,61,62,63,97,109]
- 4. Some fonts are not recognized
- \cal: [7.12.25.26,30,31,32,33,95,111] \mathbf: [30,83,111,127] \bf:[ 133,148,149]
- 5. Semi-colon is interpreted as double pipe = "||"
- [33,49,86,101]
- 6. Some code is not displayed at all.
- (This seems to be a bug of our MathJax TeX interpreter.) [67,74,78,81,83,94,101,106]
- This seems to happen when a string "\text {" is involved, can apparently be fixed by using "\text{", but still unclear.
- 7. Questions
- The different interpretation of the matrix delimiters in [56-63] is a bit surprising. Should be checked!
- Also, the vanishing of some '-' signs in the first column of some matrices, maybe that is related to 3.?
Algebraic curve
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 1.(23.) | 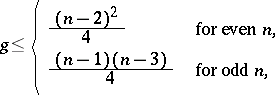
|
$g \leq \left\{ \begin{array} { l l } { \frac { ( n - 2 ) ^ { 2 } } { 4 } } & { \text { for even } n } \\ { \frac { ( n - 1 ) ( n - 3 ) } { 4 } } & { \text { for odd } n } \end{array} \right.$ | $$g\leq \left\{ \begin {array}{ll} {\frac {(n-2)^2}4} &{\text{ for even }n,}\\ {\frac {(n-1)(n-3)}4} &{\text{ for odd }n,} \end {array} \right.$$ | conf 0.698
a01145065.png (65) |
Algebraic geometry
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 2.(116.) | 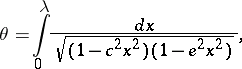
|
$\theta = \int _ { 0 } ^ { \lambda } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | $$\theta =\int\limits _ 0^{\lambda }\frac {dx}{\sqrt {(1-c^2x^2)(1-e^2x^2)}},$$ | conf 0.997
a01150014.png (14) |
| 3.(133.) | 
|
$\omega = 2 \int _ { 0 } ^ { 1 / c } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | $$\omega =2\int\limits _ 0^{1/c}\frac {dx}{\sqrt {(1-c^2x^2)(1-e^2x^2)}},$$ | conf 0.973
a01150021.png (21) |
| 4.(67.) | 
|
$\overline { w } = 2 \int _ { 0 } ^ { 1 / \varepsilon } \frac { d x } { \sqrt { ( 1 - c ^ { 2 } x ^ { 2 } ) ( 1 - e ^ { 2 } x ^ { 2 } ) } }$ | $$\widetilde w=2\int\limits _ 0^{1/\varepsilon }\frac {dx}{\sqrt {(1-c^2x^2)(1-e^2x^2)}},$$ | conf 0.107
a01150022.png (22) |
| 5.(105.) | 
|
$\theta ( v + \pi i r ) = \theta ( r ) , \quad \theta ( v + \alpha _ { j } ) = e ^ { L _ { j } ( v ) } \theta ( v )$ | $$\theta (v+\pi i r )=\theta (r),\quad \theta (v+\alpha _ j)=e^{L_j(v)}\theta (v),$$ | conf 0.775
a01150044.png (44) |
| 6.(17.) | 
|
$\left( \begin{array} { l l } { \alpha } & { b } \\ { c } & { d } \end{array} \right) \equiv \left( \begin{array} { l l } { 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) ( \operatorname { mod } 7 )$ | $$\left( \begin {array}{ll} {\alpha } &b\\ c &d \end {array} \right)\equiv \left( \begin {array}{ll} 1&0\\ 0&1 \end {array} \right)(\operatorname {mod}7).$$ | conf 0.440
a01150078.png (78) |
Algebraic surface
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 7.(144.) | 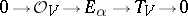
|
$0 \rightarrow O _ { V } \rightarrow E _ { \alpha } \rightarrow T _ { V } \rightarrow 0$ | $$0\rightarrow {\cal O}_V\rightarrow E _ {\alpha }\rightarrow T _ V\rightarrow 0$$ | conf 0.981
a011640132.png (132) |
| 8.(73.) | 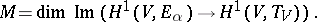
|
$M = \operatorname { dim } \operatorname { Im } ( H ^ { 1 } ( V , E _ { \alpha } ) \rightarrow H ^ { 1 } ( V , T _ { V } ) )$ | $$M=\operatorname {dim}\operatorname {Im}(H^1(V,E_{\alpha })\rightarrow H ^1(V,T_V)).$$ | conf 0.997
a011640137.png (137) |
| 9.(88.) | 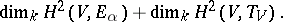
|
$\operatorname { dim } _ { k } H ^ { 2 } ( V , E _ { \alpha } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , T _ { V } )$ | $$\operatorname {dim}_kH^2(V,E_{\alpha })+\operatorname {dim}_kH^2(V,T_V).$$ | conf 0.996
a011640139.png (139) |
| 10.(117.) | 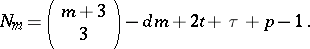
|
$N _ { m } = \left( \begin{array} { c } { m + 3 } \\ { 3 } \end{array} \right) - d m + 2 t + \tau + p - 1$ | $$N_m=\left(\begin {array}c{m+3}\\ 3 \end {array} \right)-dm+2t+\tau +p-1.$$ | conf 0.369
a01164027.png (27) |
| 11.(72.) | 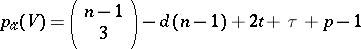
|
$p _ { \alpha } ( V ) = \left( \begin{array} { c } { n - 1 } \\ { 3 } \end{array} \right) - d ( n - 1 ) + 2 t + \tau + p - 1$ | $$p_{\alpha }(V)=\left(\begin {array}c{n-1}\\ 3 \end {array} \right)-d(n-1)+2t+\tau +p-1$$ | conf 0.396
a01164029.png (29) |
| 12.(68.)* | 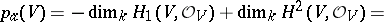
|
$p _ { x } ( V ) = - \operatorname { dim } _ { k } H _ { 1 } ( V , O _ { V } ) + \operatorname { dim } _ { k } H ^ { 2 } ( V , O _ { V } ) =$ | $$p_{\alpha }(V)=-\operatorname {dim}_kH_1(V,{\cal O}_V)+\operatorname {dim}_kH^2(V,{\cal O}_V)=$$ | conf 0.756 F
a01164047.png (47) |
| 13.(93.)* | 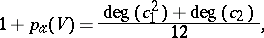
|
$1 + p _ { x } ( V ) = \frac { \operatorname { deg } ( c _ { 1 } ^ { 2 } ) + \operatorname { deg } ( c _ { 2 } ) } { 12 }$ | $$1+p_{\alpha }(V)=\frac {\operatorname {deg}(c_1^2)+\operatorname {deg}(c_2)}{12},$$ | conf 0.752 F
a01164053.png (53) |
Cartan subalgebra
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 14.(33.)* | 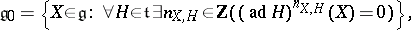
|
$\mathfrak { g } 0 = \{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists \mathfrak { n } X , H \in Z ( ( \text { ad } H ) ^ { n } X , H ( X ) = 0 ) \}$ | $$\mathfrak g_0=\big\{X\in \mathfrak g:\forall H \in \mathfrak t\exists n_{X,H}\in {\mathbb Z}((\text{ ad }H)^{n_{X,H}}(X)=0)\big\},$$ | conf 0.110 F
c0205509.png (9) |
Cartan theorem
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 15.(49.)* | 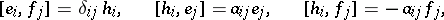
|
$f _ { j } ] = \delta _ { i j } h _ { i } , \quad [ h _ { i } , e _ { j } ] = \alpha _ { i j } e _ { j } , \quad [ h _ { i } , f _ { j } ] = - \alpha _ { j } f _ { j }$ | $$[e_i,f_j]=\delta _ {ij}h_i,\quad [h_i,e_j]=\alpha _ {ij}e_j,\quad [h_i,f_j]=-\alpha _ {ij}f_j,$$ | conf 0.149 F
c0205704.png (4) |
| 16.(55.)* | 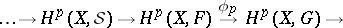
|
$\rightarrow H ^ { p } ( X , S ) \rightarrow H ^ { p } ( X , F ) \stackrel { \phi p } { \rightarrow } H ^ { p } ( X , G ) \rightarrow$ | $$\dots \rightarrow H ^p(X,S)\rightarrow H ^p(X,F)\stackrel {\phi_p }{\rightarrow }H^p(X,G)\rightarrow $$ | conf 0.853 F
c02057064.png (64) |
Comitant
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 17.(7.) | 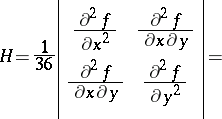
|
$H = \frac { 1 } { 36 } \left| \begin{array} { c c } { \frac { \partial ^ { 2 } f } { \partial x ^ { 2 } } } & { \frac { \partial ^ { 2 } f } { \partial x \partial y } } \\ { \frac { \partial ^ { 2 } f } { \partial x \partial y } } & { \frac { \partial ^ { 2 } f } { \partial y ^ { 2 } } } \end{array} \right| =$ | $$H=\frac 1{36}\left| \begin {array}{cc} {\frac {\partial ^2f}{\partial x ^2}} &{\frac {\partial ^2f}{\partial x \partial y }}\\ {\frac {\partial ^2f}{\partial x \partial y }} &{\frac {\partial ^2f}{\partial y ^2}} \end {array} \right|=$$ | conf 0.956
c02333033.png (33) |
| 18.(76.) | 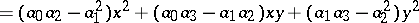
|
$= ( a _ { 0 } a _ { 2 } - a _ { 1 } ^ { 2 } ) x ^ { 2 } + ( a _ { 0 } a _ { 3 } - a _ { 1 } a _ { 2 } ) x y + ( a _ { 1 } a _ { 3 } - a _ { 2 } ^ { 2 } ) y ^ { 2 }$ | $$=(a_0a_2-a_1^2)x^2+(a_0a_3-a_1a_2)xy+(a_1a_3-a_2^2)y^2$$ | conf 0.549
c02333034.png (34) |
| 19.(11.)* | 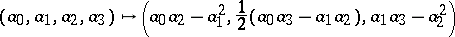
|
$( \alpha _ { 0 } , \alpha _ { 1 } , \alpha _ { 2 } , \alpha _ { 3 } ) \mapsto ( \alpha _ { 0 } \alpha _ { 2 } - \alpha _ { 1 } ^ { 2 } , \frac { 1 } { 2 } ( \alpha _ { 0 } \alpha _ { 3 } - \alpha _ { 1 } \alpha _ { 2 } ) , \alpha _ { 1 } \alpha _ { 3 } - \alpha _ { 2 } ^ { 2 } )$ | $$(\alpha _ 0,\alpha _ 1,\alpha _ 2,\alpha _ 3)\mapsto (\alpha _ 0\alpha _ 2-\alpha _ 1^2,\frac 12(\alpha _ 0\alpha _ 3-\alpha _ 1\alpha _ 2),\alpha _ 1\alpha _ 3-\alpha _ 2^2)$$ | conf 0.521 F
c02333035.png (35) |
Deformation
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 20.(26.) | 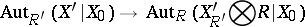
|
$\operatorname { Aut } _ { R ^ { \prime } } ( X ^ { \prime } | X _ { 0 } ) \rightarrow \operatorname { Aut } _ { R } ( X _ { R ^ { \prime } } ^ { \prime } \otimes R | X _ { 0 } )$ | $$\operatorname {Aut}_{R^{\prime }}(X^{\prime }|X_0)\rightarrow \operatorname {Aut}_R(X_{R^{\prime }}^{\prime }\otimes R |X_0)$$ | conf 0.683
\ d030700175.png (175) |
| 21.(27.) | 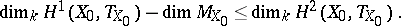
|
$\operatorname { dim } _ { k } H ^ { 1 } ( X _ { 0 } , T _ { X _ { 0 } } ) - \operatorname { dim } M _ { X _ { 0 } } \leq \operatorname { dim } _ { k } H ^ { 2 } ( X _ { 0 } , T _ { X _ { 0 } } )$ | $$\operatorname {dim}_kH^1(X_0,T_{X_0})-\operatorname {dim}M_{X_0}\leq \operatorname {dim}_kH^2(X_0,T_{X_0}).$$ | conf 0.944
d030700190.png (190) |
| 22.(78.)* | 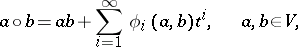
|
$\alpha \circ b = \alpha b + \sum _ { i = 1 } ^ { \infty } \phi _ { i } ( \alpha , b ) t ^ { i } , \quad \alpha , b \in V$ | $$\alpha \circ b =\alpha b +\sum _ {i=1}^{\infty }\phi _ i(\alpha ,b)t^i,\quad \alpha ,b\in V,$$ | conf 0.097 F
d030700263.png (263) |
| 23.(96.)* | 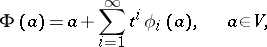
|
$\Phi ( \alpha ) = \alpha + \sum _ { i = 1 } ^ { \infty } t ^ { i } \phi _ { i } ( \alpha ) , \quad \alpha \in V$ | $$\Phi (\alpha )=\alpha +\sum _ {i=1}^{\infty }t^i\phi _ i(\alpha ),\quad \alpha \in V,$$ | conf 0.873 F
d030700270.png (270) |
Differential algebra
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 24.(106.) | 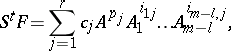
|
$S ^ { t } F = \sum _ { j = 1 } ^ { r } c _ { j } A ^ { p _ { j } } A _ { 1 } ^ { i _ { 1 j } } \dots A _ { m - l } ^ { i _ { m - l } , j }$ | $$S^tF=\sum _ {j=1}^rc_jA^{p_j}A_1^{i_{1j}}\dots A _ {m-l}^{i_{{m-l},j}},$$ | conf 0.149
d031830107.png (107) |
| 25.(146.)* | 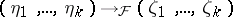
|
$( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$ | $(\eta _ 1,\ldots ,\eta _ k)\rightarrow {}_{\cal F}(\zeta _ 1,\ldots ,\zeta _ k)$ | conf 0.562 F
d031830141.png (141) |
| 26.(145.)$^F$* | 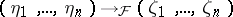
|
$( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$ | $(\eta _ 1,\ldots ,\eta _ n)\rightarrow {}_{\cal F}(\zeta _ 1,\ldots ,\zeta _ n)$ | conf 0.376 F
d031830150.png (150) |
| 27.(57.) | 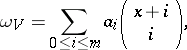
|
$\omega _ { V } = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$ | $$\omega _ V=\sum _ {0\leq i \leq m }\alpha _ i\left( \begin {array}c{x+i}\\ i \end {array} \right),$$ | conf 0.780
d03183016.png (16) |
| 28.(111.) | 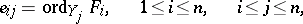
|
$e _ { i j } = \operatorname { ord } _ { Y } _ { j } F _ { i } , \quad 1 \leq i \leq n , \quad i \leq j \leq n$ | $$e_{ij}=\operatorname {ord}_{Y_j}F_i,\quad 1 \leq i \leq n ,\quad i \leq j \leq n,$$ | conf 0.187
d03183043.png (43) |
Dimension polynomial
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 29.(48.) | 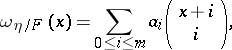
|
$\omega _ { \eta / F } ( x ) = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right)$ | $$\omega _ {\eta /F}(x)=\sum _ {0\leq i \leq m }\alpha _ i\left(\begin {array}c{x+i}\\ i \end {array} \right),$$ | conf 0.968
d03249029.png (29) |
Duality
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file | |
|---|---|---|---|---|---|
| 30.(118.)* | 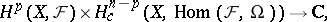
|
$H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow C$ | $$H^p(X,{\cal F})\times H _ c^{n-p}(X,\operatorname {Hom}({\cal F},\Omega ))\rightarrow {\mathbf C},$$ | conf 0.824 F
d034120173.png (173) | |
| 31.(59.)* | 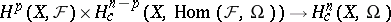
|
$H ^ { p } ( X , F ) \times H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) ) \rightarrow H _ { c } ^ { n } ( X , \Omega )$ | $$H^p(X,{\cal F})\times H _ c^{n-p}(X,\operatorname {Hom}({\cal F},\Omega ))\rightarrow H _ c^n(X,\Omega )$$ | conf 0.921 F
d034120175.png (175) | |
| 32.(124.)* | 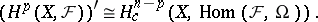
|
$( H ^ { p } ( X , F ) ) ^ { \prime } \cong H _ { c } ^ { n - p } ( X , \operatorname { Hom } ( F , \Omega ) )$ | $$(H^p(X,{\cal F}))^{\prime }\cong H _ c^{n-p}(X,\operatorname {Hom}({\cal F},\Omega )).$$ | conf 0.829 F
d034120184.png (184) | |
| 33.(29.)* | 
|
$\beta : \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X F , \Omega ) \rightarrow \operatorname { Ext } _ { c } ^ { n - p - 1 } ( X \backslash Y || F , \Omega )$ | $$\beta :\operatorname {Ext}_c^{n-p-1}(X;{\cal F},\Omega )\rightarrow \operatorname {Ext}_c^{n-p-1}(X\backslash Y ;{\cal F},\Omega ).$$ | conf 0.634 | F
d034120236.png (236) |
| 34.(77.)* | 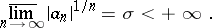
|
$\underset { n \rightarrow \infty } { \operatorname { lim } } | \alpha _ { n } | ^ { 1 / n } = \sigma < + \infty$ | $$\underset {n\rightarrow \infty }{\overline {\lim }}|\alpha _ n|^{1/n}=\sigma <+\infty.$$ | conf 0.521 F
d034120247.png (247) | |
| 35.(58.)* | 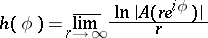
|
$h ( \phi ) = \operatorname { lim } _ { r \rightarrow \infty } \frac { \operatorname { ln } | A ( r e ^ { i \phi } ) | } { r }$ | $$h(\phi )=\underset {n\rightarrow \infty }{\overline {\lim }}\frac {\operatorname {ln}|A(re^{i\phi })|}r$$ | conf 0.861 F
d034120253.png (253) | |
| 36.(69.)* | 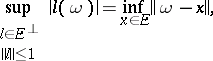
|
$\operatorname { sup } _ { l \in E ^ { \perp } } | l ( \omega ) | = \operatorname { inf } _ { x \in E } \| \omega - x \|$ | $$\operatorname*{sup}_{l\in E^\perp \atop \|l\|\le 1 }|l(\omega )|=\operatorname*{inf}_{x\in E }\|\omega -x\|,$$ | conf 0.293 F
d034120360.png (360) | |
| 37.(15.) | 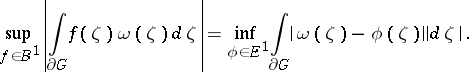
|
$\operatorname { sup } _ { f \in B ^ { 1 } } | \int _ { \partial G } f ( \zeta ) \omega ( \zeta ) d \zeta | = \operatorname { inf } _ { \phi \in E ^ { 1 } } \int _ { \partial G } | \omega ( \zeta ) - \phi ( \zeta ) \| d \zeta |$ | $$\operatorname*{sup}_{f\in B ^1}\big|\int\limits _ {\partial G }f(\zeta )\omega (\zeta )d\zeta \big|=\operatorname*{inf}_{\phi \in E ^1}\int\limits _ {\partial G }|\omega (\zeta )-\phi (\zeta ) ||d\zeta |.$$ | conf 0.508
d034120376.png (376) | |
| 38.(52.) | 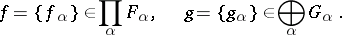
|
$f = \{ f _ { \alpha } \} \in \prod _ { \alpha } F _ { \alpha } , \quad g = \{ g _ { \alpha } \} \in \oplus _ { \alpha } G _ { \alpha }$ | $$f=\{f_{\alpha }\}\in \prod _ {\alpha }F_{\alpha },\quad g =\{g_{\alpha }\}\in \operatorname*\oplus _ {\alpha }G_{\alpha }.$$ | conf 0.491
d034120509.png (509) | |
| 39.(140.) | 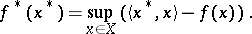
|
$f ^ { * } ( x ^ { * } ) = \operatorname { sup } _ { x \in X } ( \langle x ^ { * } , x \rangle - f ( x ) )$ | $$f^{*}(x^{*})=\operatorname*{sup}_{x\in X }(\langle x ^{*},x\rangle -f(x))$$ | conf 0.900
d034120535.png (535) | |
| 40.(94.) | 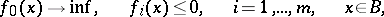
|
$f _ { 0 } ( x ) \rightarrow \text { inf, } \quad f _ { i } ( x ) \leq 0 , \quad i = 1 , \ldots , m , \quad x \in B$ | $$f_0(x)\rightarrow \text{ inf, }\quad f _ i(x)\leq 0 ,\quad i =1,\ldots ,m,\quad x \in B,$$ | conf 0.810
d034120555.png (555) | |
| 41.(74.)* | 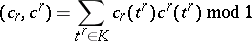
|
$( c _ { \gamma } , c ^ { r } ) = \sum _ { t ^ { r } \in K } c _ { r } ( t ^ { \prime } ) c ^ { r } ( t ^ { r } ) \operatorname { mod } 1$ | $$(c_{\gamma },c^r)=\sum _ {t^r\in K }c_r(t^{\prime })c^r(t^r)\operatorname {mod}1$$ | conf 0.117 F
d03412079.png (79) |
Extension of a differential field
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 42.(63.) | 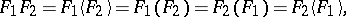
|
$F _ { 1 } F _ { 2 } = F _ { 1 } \langle F _ { 2 } \rangle = F _ { 1 } ( F _ { 2 } ) = F _ { 2 } ( F _ { 1 } ) = F _ { 2 } \langle F _ { 1 } \rangle$ | $$F_1F_2=F_1\langle F _ 2\rangle =F_1(F_2)=F_2(F_1)=F_2\langle F _ 1\rangle,$$ | conf 0.628
e03696024.png (24) |
Formal group
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 43.(120.)* | 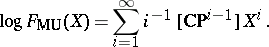
|
$\operatorname { og } F _ { MU } ( X ) = \sum _ { i = 1 } ^ { \infty } i ^ { - 1 } [ C ^ { - } P ^ { - 1 } ] X ^ { i }$ | $$\operatorname {log}F_{\rm MU }(X)=\sum _ {i=1}^{\infty }i^{-1}[{\rm CP}^{i-1}]X^i,$$ | conf 0.098 F
f040820118.png (118) |
| 44.(147.)* | 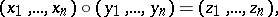
|
$( x _ { 1 } , \ldots , x _ { x } ) \circ ( y _ { 1 } , \ldots , y _ { n } ) = ( z _ { 1 } , \ldots , z _ { x } )$ | $$(x_1,\ldots ,x_n)\circ (y_1,\ldots ,y_n)=(z_1,\ldots ,z_n),$$ | conf 0.553 F
f04082059.png (59) |
Gel'fond-Schneider method
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 45.(148.) | 
|
$\alpha ^ { \beta } = \operatorname { exp } \{ \beta \operatorname { log } \alpha \}$ | $\alpha ^{\beta }=\operatorname {exp}\{\beta \operatorname {log}\alpha \}$ | conf 0.979
g1300205.png (5) |
Group
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 46.(22.)* | 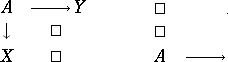
|
$\left. \begin{array} { l l l } { A } & { \rightarrow Y } & { \square } \\ { \downarrow } & { \square } & { } & { \square } \\ { X } & { \square } & { } & { A } \end{array} \right.$ | source incomplete | conf 0.226 F
g04521075.png (75) |
Homogeneous space
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 47.(89.) | 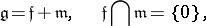
|
$\mathfrak { g } = \mathfrak { f } + \mathfrak { m } , \quad \mathfrak { f } \cap \mathfrak { m } = \{ 0 \}$ | $$\mathfrak g=\mathfrak f+\mathfrak m,\quad \mathfrak f\cap \mathfrak m=\{0\},$$ | conf 0.793
h04769069.png (69) |
Hopf algebra
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 48.(103.) | 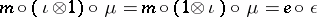
|
$m \circ ( \iota \otimes 1 ) \circ \mu = m \circ ( 1 \otimes \iota ) \circ \mu = e \circ \epsilon$ | $m\circ (\iota \otimes 1 )\circ \mu =m\circ (1\otimes \iota )\circ \mu =e\circ \epsilon$ | conf 0.618
h047970129.png (129) |
| 49.(107.)* | 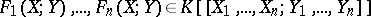
|
$F _ { 1 } ( X || Y ) , \ldots , F _ { n } ( X || Y ) \in K [ X _ { 1 } , \ldots , X _ { n } || Y _ { 1 } , \ldots , Y _ { n } ] \}$ | $F_1(X;Y),\ldots ,F_n(X;Y)\in K [X_1,\ldots ,X_n;Y_1,\ldots ,Y_n]\}$ | conf 0.353 F
h047970139.png (139) |
| 50.(97.) | 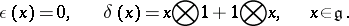
|
$\epsilon ( x ) = 0 , \quad \delta ( x ) = x \bigotimes 1 + 1 \bigotimes x , \quad x \in \mathfrak { g }$ | $$\epsilon (x)=0,\quad \delta (x)=x\otimes 1 +1\otimes x ,\quad x \in \mathfrak g.$$ | conf 0.213
h04797042.png (42) |
Invariants, theory of
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 51.(149.)* | 
|
$\alpha _ { 1 } , \ldots , i _ { R } \rightarrow \alpha _ { 2 } ^ { \prime } , \ldots , i _ { R }$ | $$\alpha _ {i_1,\dots,i_n}\rightarrow \alpha _ {i_1,\dots,i_n}^{\prime }.$$ | conf 0.142 F
i05235015.png (15) |
Jordan algebra
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 52.(150.) | 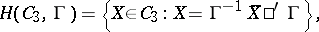
|
$H ( C _ { 3 } , \Gamma ) = \{ X \in C _ { 3 } : X = \Gamma ^ { - 1 } X \square ^ { \prime } \Gamma \}$ | $$(C_3,\Gamma )=\big\{X\in C _ 3:X=\Gamma ^{-1}X\square ^{\prime }\Gamma \big\},$$ | conf 0.651
j05427030.png (30) |
| 53.(42.) | 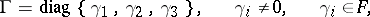
|
$\Gamma = \operatorname { diag } \{ \gamma _ { 1 } , \gamma _ { 2 } , \gamma _ { 3 } \} , \quad \gamma _ { i } \neq 0 , \quad \gamma _ { i } \in F$ | $$\Gamma =\operatorname {diag}\{\gamma _ 1,\gamma _ 2,\gamma _ 3\},\quad \gamma _ i\neq 0 ,\quad \gamma _ i\in F,$$ | conf 0.987
j05427031.png (31) |
| 54.(125.)* | 
|
$\mathfrak { g } = \mathfrak { g } - 1 + \mathfrak { g } \mathfrak { d } + \mathfrak { g } _ { 1 }$ | $\mathfrak g=\mathfrak g_{-1}+\mathfrak g_0+\mathfrak g_1$ | conf 0.598 F
j05427077.png (77) |
Jordan matrix
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 55.(6.)* | 
|
$J = \left| \begin{array} { c c c c } { J _ { n _ { 1 } } ( \lambda _ { 1 } ) } & { \square } & { \square } & { \square } \\ { \square } & { \ldots } & { \square } & { 0 } \\ { 0 } & { \square } & { \ldots } & { \square } \\ { \square } & { \square } & { \square } & { J _ { n _ { S } } ( \lambda _ { s } ) } \end{array} \right|$ | $$J=\left\| \begin {array}{cccc} J_{n_1}(\lambda_1) &0 &0 &0\\ 0 &\ddots &\ddots &0\\ 0 &\ddots &\ddots &0\\ 0 &0 &0 &J_{n_s}(\lambda_s) \end {array} \right\|,$$ | conf 0.072 F
j0543403.png (3) |
| 56.(64.) | 
|
$C _ { m } ( \lambda ) = \operatorname { rk } ( A - \lambda E ) ^ { m - 1 } - 2 \operatorname { rk } ( A - \lambda E ) ^ { m } +$ | $$C_m(\lambda )=\operatorname {rk}(A-\lambda E )^{m-1}-2\operatorname {rk}(A-\lambda E )^m+$$ | conf 0.955
j05434030.png (30) |
| 57.(1.)* | 
|
$J _ { m } ( \lambda ) = \| \begin{array} { c c c c c c } { \lambda } & { 1 } & { \square } & { \square } & { \square } & { \square } \\ { \square } & { \lambda } & { 1 } & { \square } & { 0 } & { \square } \\ { \square } & { \square } & { \cdots } & { \square } & { \square } & { \square } \\ { \square } & { \square } & { \square } & { \cdots } & { \square } & { \square } \\ { \square } & { 0 } & { \square } & { \square } & { \lambda } & { 1 } \\ { \square } & { \square } & { \square } & { \square } & { \square } & { \lambda } \end{array} ]$ | $$J_m(\lambda)=\left\| \begin {array}{cccccc} \lambda &1 &\square &\square &\square &\square \\ \square &\lambda &1 &\square &0 &\square \\ \square &\square &\ddots &\ddots &\square &\square\\ \square &\square &\square &\ddots &\ddots &\square \\ \square &0 &\square &\square &\lambda &1\\ \square &\square &\square &\square &\square &\lambda \end {array} \right\|,$$ | conf 0.098 F
j0543406.png (6) |
Lie algebra, semi-simple
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 58.(5.) | 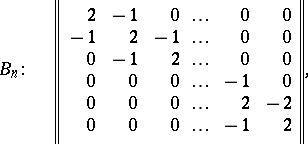
|
$\left\| \begin{array} { r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 2 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } \end{array} \right\|$ | $$B_n:\quad \left\| \begin {array}{rrrrrr} 2 &{-1} &0 &{\dots } &0 &0\\ {-1} &2 &{-1} &{\dots } &0 &0\\ 0 &{-1} &2 &{\dots } &0 &0\\ \cdot &\cdot &\cdot &\dots &\cdot &\cdot \\ 0 &0 &0 &{\dots } &{-1} &0\\ 0 &0 &0 &{\dots } &2 &{-2}\\ 0 &0 &0 &{\dots } &{-1} &2 \end {array} \right\|,$$ | conf 0.232
l058510127.png (127) |
| 59.(3.)* | 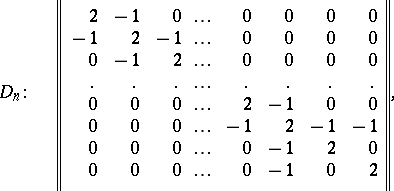
|
$\| \left. \begin{array} { r r r r r r r } { 2 } & { - 1 } & { 0 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 1 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { \dots } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { - 1 } & { 2 } & { - 1 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 2 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { \dots } & { 0 } & { - 1 } & { 0 } & { 2 } \end{array} \right. |$ | $$D_n:\quad \left\| \begin {array}{rrrrrrr} 2 &{-1} &0 &{\dots } &0 &0 &0 &0\\ {-1} &2 &{-1} &{\dots } &0 &0 &0 &0\\ 0 &{-1} &2 &{\dots } &0 &0 &0 &0\\ \cdot &\cdot &\cdot &\dots &\cdot &\cdot &\cdot &\cdot \\ 0 &0 &0 &{\dots } &2 &{-1} &0 &0\\ 0 &0 &0 &{\dots } &{-1} &2 &{-1} &{-1}\\ 0 &0 &0 &{\dots } &0 &{-1} &2 &0\\ 0 &0 &0 &{\dots } &0 &{-1} &0 &2 \end {array} \right\|,$$ | conf 0.055 F
l058510129.png (129) |
| 60.(8.)* | 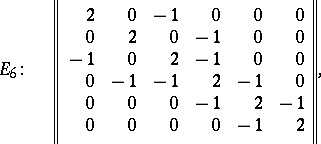
|
$\left\| \begin{array} { r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$ | $$E_6: \quad \left\| \begin {array}{rrrrrr} 2 &0 &{-1} &0 &0 &0\\ 0 &2 &0 &{-1} &0 &0\\ {-1} &0 &2 &{-1} &0 &0\\ 0 &{-1} &{-1} &2 &{-1} &0\\ 0 &0 &0 &{-1} &2 &{-1}\\ 0 &0 &0 &0 &{-1} &2 \end {array} \right\|,$$ | conf 0.628 F
l058510130.png (130) |
| 61.(4.) | 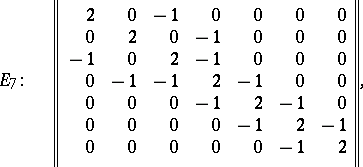
|
$\left\| \begin{array} { r r r r r r r } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\|$ | $$E_7:\quad \left\| \begin {array}{rrrrrrr} 2 &0 &{-1} &0 &0 &0 &0\\ 0 &2 &0 &{-1} &0 &0 &0\\ {-1} &0 &2 &{-1} &0 &0 &0\\ 0 &{-1} &{-1} &2 &{-1} &0 &0\\ 0 &0 &0 &{-1} &2 &{-1} &0\\ 0 &0 &0 &0 &{-1} &2 &{-1}\\ 0 &0 &0 &0 &0 &{-1} &2 \end {array} \right\|,$$ | conf 0.278
l058510131.png (131) |
| 62.(2.)* | 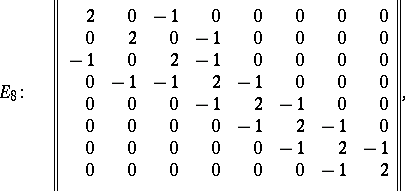
|
$\left. \begin{array} { r l l l l l l l } { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 2 } & { 0 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 1 } & { 0 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right.$ | $$E_8:\quad \left\| \begin {array}{rrrrrrrr} 2 &0 &{-1} &0 &0 &0 &0 & 0\\ 0 &2 &0 &{-1} &0 &0 &0 &0\\ {-1} &0 &2 &{-1} &0 &0 &0 &0\\ 0 &{-1} &{-1} &2 &{-1} &0 &0 &0\\ 0 &0 &0 &{-1} &2 &{-1} &0 &0\\ 0 &0 &0 &0 &{-1} &2 &{-1} &0\\ 0 &0 &0 &0 &0 &{-1} &2 &{-1}\\ 0 &0 &0 &0 &0 &0 &{-1} &2 \end {array} \right\|,$$ | conf 0.354 F
l058510132.png (132) |
| 63.(10.)* | 
|
$\left\| \begin{array} { r r r r } { 2 } & { - 1 } & { 0 } & { 0 } \\ { - 1 } & { 2 } & { - 2 } & { 0 } \\ { 0 } & { - 1 } & { 2 } & { - 1 } \\ { 0 } & { 0 } & { - 1 } & { 2 } \end{array} \right\| , \quad G _ { 2 } : \quad \left\| \begin{array} { r r } { 2 } & { - 1 } \\ { - 3 } & { 2 } \end{array} \right\|$ | $$F_4:\quad \left\| \begin {array}{rrrr} 2 &{-1} &0 &0\\ {-1} &2 &{-2} &0\\ 0 &{-1} &2 &{-1}\\ 0 &0 &{-1} &2 \end {array} \right\|,\quad G _ 2:\quad \left\| \begin {array}{rr} 2&{-1}\\ {-3}&2 \end {array} \right\|.$$ | conf 0.374 F
l058510133.png (133) |
| 64.(98.) | 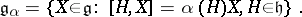
|
$\mathfrak { g } _ { \alpha } = \{ X \in \mathfrak { g } : [ H , X ] = \alpha ( H ) X , H \in \mathfrak { h } \}$ | $$\mathfrak g_{\alpha }=\{X\in \mathfrak g:[H,X]=\alpha (H)X,H\in \mathfrak h\}.$$ | conf 0.976
l05851030.png (30) |
| 65.(126.) | 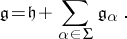
|
$\mathfrak { g } = \mathfrak { h } + \sum _ { \alpha \in \Sigma } \mathfrak { g } _ { \alpha }$ | $$\mathfrak g=\mathfrak h+\sum _ {\alpha \in \Sigma }\mathfrak g_{\alpha }.$$ | conf 0.945
l05851037.png (37) |
| 66.(61.)* | 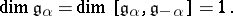
|
$\mathfrak { g } _ { \alpha } = \operatorname { dim } [ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { - \alpha } ] = 1$ | $$\mathfrak g_{\alpha }=\operatorname {dim}[\mathfrak g_{\alpha },\mathfrak g_{-\alpha }]=1.$$ | conf 0.520 F
l05851044.png (44) |
| 67.(65.)* | 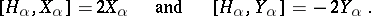
|
$[ H _ { \alpha } , X _ { \alpha } ] = 2 X _ { \alpha } \quad \text { and } \quad [ H _ { \alpha } , Y _ { \alpha } ] = - 2 Y _ { 0 }$ | $$[H_{\alpha },X_{\alpha }]=2X_{\alpha }\quad {\rm and }\quad [H_{\alpha },Y_{\alpha }]=-2Y_{\alpha }.$$ | conf 0.539 F
l05851050.png (50) |
| 68.(70.) | 
|
$\beta ( H _ { \alpha } ) = \frac { 2 ( \alpha , \beta ) } { ( \alpha , \alpha ) } , \quad \alpha , \beta \in \Sigma$ | $$\beta (H_{\alpha })=\frac {2(\alpha ,\beta )}{(\alpha ,\alpha )},\quad \alpha ,\beta \in \Sigma,$$ | conf 0.997
l05851051.png (51) |
| 69.(112.) | 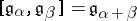
|
$[ \mathfrak { g } _ { \alpha } , \mathfrak { g } _ { \beta } ] = \mathfrak { g } _ { \alpha + \beta }$ | $$[\mathfrak g_{\alpha },\mathfrak g_{\beta }]=\mathfrak g_{\alpha +\beta }$$ | conf 0.917
l05851057.png (57) |
| 70.(127.) | 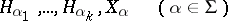
|
$H _ { \alpha _ { 1 } } , \ldots , H _ { \alpha _ { k } } , X _ { \alpha } \quad ( \alpha \in \Sigma )$ | $$H_{\alpha _ 1},\ldots ,H_{\alpha _ k},X_{\alpha }\quad (\alpha \in \Sigma )$$ | conf 0.432
l05851064.png (64) |
| 71.(113.)* | 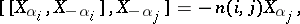
|
$[ [ X _ { \alpha _ { i } } , X _ { - } \alpha _ { i } ] , X _ { - \alpha _ { j } } ] = - n ( i , j ) X _ { \alpha _ { j } }$ | $$[[X_{\alpha _ i},X_{-}\alpha _ i],X_{-\alpha _ j}]=-n(i,j)X_{\alpha _ j},$$ | conf 0.628 F
l05851069.png (69) |
| 72.(79.) | 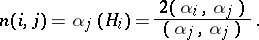
|
$n ( i , j ) = \alpha _ { j } ( H _ { i } ) = \frac { 2 ( \alpha _ { i } , \alpha _ { j } ) } { ( \alpha _ { j } , \alpha _ { j } ) }$ | $$n(i,j)=\alpha _ j(H_i)=\frac {2(\alpha _ i,\alpha _ j)}{(\alpha _ j,\alpha _ j)}.$$ | conf 0.992
l05851073.png (73) |
| 73.(13.) | 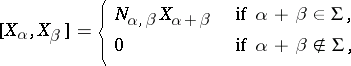
|
$[ X _ { \alpha } , X _ { \beta } ] = \left\{ \begin{array} { l l } { N _ { \alpha , \beta } X _ { \alpha + \beta } } & { \text { if } \alpha + \beta \in \Sigma } \\ { 0 } & { \text { if } \alpha + \beta \notin \Sigma } \end{array} \right.$ | $$[X_{\alpha },X_{\beta }]=\left\{ \begin {array}{ll} {N_{\alpha ,\beta }X_{\alpha +\beta }} &{\text{ if }\alpha +\beta \in \Sigma,}\\ 0 &{\text{ if }\alpha +\beta \notin \Sigma,} \end {array} \right.$$ | conf 0.988
l05851074.png (74) |
| 74.(80.) | 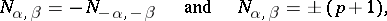
|
$N _ { \alpha , \beta } = - N _ { - \alpha , - \beta } \quad \text { and } \quad N _ { \alpha , \beta } = \pm ( p + 1 )$ | $$N_{\alpha ,\beta }=-N_{-\alpha ,-\beta }\quad {\rm and }\quad N _ {\alpha ,\beta }=\pm (p+1),$$ | conf 0.961
l05851078.png (78) |
| 75.(85.)* | 
|
$X _ { \alpha } - X _ { - \alpha } , \quad i ( X _ { \alpha } + X _ { - \alpha } ) \quad ( \alpha \in \Sigma _ { + } )$ | $$iH_\alpha,X_{\alpha }-X_{-\alpha },\quad i (X_{\alpha }+X_{-\alpha })\quad (\alpha \in \Sigma _ {+})$$ | conf 0.691 F
l05851085.png (85) |
Lie algebra, solvable
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 76.(119.)* | 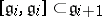
|
$[ \mathfrak { g } _ { i } , \mathfrak { g } _ { i } ] \subset \mathfrak { g } _ { \mathfrak { i } } + 1$ | $[\mathfrak g_i,\mathfrak g_i]\subset \mathfrak g_{i+1}$ | conf 0.276 F
l05852011.png (11) |
| 77.(141.) | 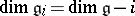
|
$\operatorname { dim } \mathfrak { g } _ { i } = \operatorname { dim } \mathfrak { g } - i$ | $\operatorname {dim}\mathfrak g_i=\operatorname {dim}\mathfrak g-i$ | conf 0.901
l05852046.png (46) |
Lie group
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 78.(62.)* | 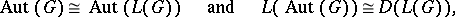
|
$( G ) \cong \operatorname { Aut } ( L ( G ) ) \quad \text { and } \quad L ( \operatorname { Aut } ( G ) ) \cong D ( L ( G ) )$ | $$\operatorname {Aut}(G)\cong \operatorname {Aut}(L(G))\quad {\rm and }\quad L (\operatorname {Aut}(G))\cong D (L(G)),$$ | conf 0.693 F
l058590115.png (115) |
| 79.(50.) | 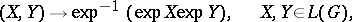
|
$( X , Y ) \rightarrow \operatorname { exp } ^ { - 1 } ( \operatorname { exp } X \operatorname { exp } Y ) , \quad X , Y \in L ( G )$ | $$(X,Y)\rightarrow \operatorname {exp}^{-1}(\operatorname {exp}X\operatorname {exp}Y),\quad X ,Y\in L (G),$$ | conf 0.856
l05859086.png (86) |
Lie group, compact
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 80.(121.)* | 
|
$J = \left\| \begin{array} { c c } { 0 } & { E _ { x } } \\ { - E _ { x } } & { 0 } \end{array} \right\|$ | $$J=\left\| \begin {array}{cc} 0 &{E_x}\\ {-E_x} &0 \end {array} \right\|,$$ | conf 0.364 F
l05861012.png (12) |
Lie group, nilpotent
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 81.(83.) | 
|
$N ( F ) = \{ g \in GL ( V ) : g v \equiv v \operatorname { mod } V _ { i } \text { for all } v \in V _ { i } , i \geq 1 \}$ | $$N(F)=\{g\in GL (V):gv\equiv v \operatorname {mod}V_i\;\text{for all }v\in V _ i,\;i\geq 1 \}$$ | conf 0.466
l0586604.png (4) |
Lie group, semi-simple
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 82.(35.)* | 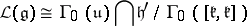
|
$L ( \mathfrak { g } ) \cong \Gamma _ { 0 } ( \mathfrak { u } ) \cap \mathfrak { h } ^ { \prime } / \Gamma _ { 0 } ( [ \mathfrak { k } , \mathfrak { k } ] )$ | $$L(\mathfrak g)\cong \Gamma _ 0(\mathfrak u)\cap \mathfrak h^{\prime }/\Gamma _ 0([\mathfrak k,\mathfrak k])$$ | conf 0.659 F
l058680102.png (102) |
| 83.(81.)* | 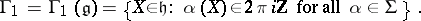
|
$\Gamma _ { 1 } = \Gamma _ { 1 } ( g ) = \{ X \in h : \alpha ( X ) \in 2 \pi i Z \text { for all } \alpha \in \Sigma \}$ | $$\Gamma _ 1=\Gamma _ 1(g)=\{X\in h :\alpha (X)\in 2 \pi i {\mathbf Z}\;\text{for all }\alpha \in \Sigma \}.$$ | conf 0.183 F
l05868032.png (32) |
Lie p-algebra
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 84.(36.) | 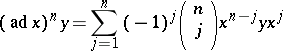
|
$( \operatorname { ad } x ) ^ { n } y = \sum _ { j = 1 } ^ { n } ( - 1 ) ^ { j } \left( \begin{array} { c } { n } \\ { j } \end{array} \right) x ^ { n - j } y x ^ { j }$ | $$(\operatorname {ad}x)^ny=\sum _ {j=1}^n(-1)^j\left(\begin {array}cn\\ j \end {array} \right)x^{n-j}yx^j$$ | conf 0.356
l05872026.png (26) |
| 85.(99.) | 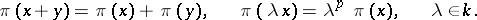
|
$\pi ( x + y ) = \pi ( x ) + \pi ( y ) , \quad \pi ( \lambda x ) = \lambda ^ { p } \pi ( x ) , \quad \lambda \in k$ | $$\pi (x+y)=\pi (x)+\pi (y),\quad \pi (\lambda x )=\lambda ^p\pi (x),\quad \lambda \in k .$$ | conf 0.964
l05872078.png (78) |
Lie theorem
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 86.(134.) | 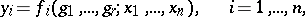
|
$y _ { i } = f _ { i } ( g _ { 1 } , \ldots , g _ { i } || x _ { 1 } , \ldots , x _ { n } ) , \quad i = 1 , \ldots , n$ | $$y_i=f_i(g_1,\ldots ,g_i;x_1,\ldots ,x_n),\quad i =1,\ldots ,n$$ | conf 0.276
l05876010.png (10) |
| 87.(86.) | 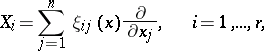
|
$X _ { i } = \sum _ { j = 1 } ^ { n } \xi _ { i j } ( x ) \frac { \partial } { \partial x _ { j } } , \quad i = 1 , \ldots , r$ | $$X_i=\sum _ {j=1}^n\xi _ {ij}(x)\frac {\partial }{\partial x _ j},\quad i =1,\ldots ,r,$$ | conf 0.656
l05876016.png (16) |
| 88.(66.)* | 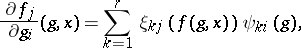
|
$\frac { \partial f _ { j } } { \partial g _ { i } } ( g , x ) = \sum _ { k = 1 } ^ { r } \xi _ { k j } ( f ( g _ { s } x ) ) \psi _ { k i } ( g )$ | $$\frac {\partial f _ j}{\partial g _ i}(g,x)=\sum _ {k=1}^r\xi _ {kj}(f(g_sx))\psi _ {ki}(g),$$ | conf 0.336 F
l05876030.png (30) |
| 89.(19.)* | 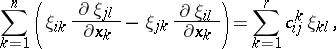
|
$\sum _ { k = 1 } ^ { N } ( \xi _ { i k } \frac { \partial \xi _ { j l } } { \partial x _ { k } } - \xi _ { j k } \frac { \partial \xi _ { i l } } { \partial x _ { k } } ) = \sum _ { k = 1 } ^ { r } c _ { i j } ^ { k } \xi _ { k l }$ | $$\sum _ {k=1}^N(\xi _ {ik}\frac {\partial \xi _ {jl}}{\partial x _ k}-\xi _ {jk}\frac {\partial \xi _ {il}}{\partial x _ k})=\sum _ {k=1}^rc_{ij}^k\xi _ {kl},$$ | conf 0.157 F
l05876037.png (37) |
| 90.(14.) | 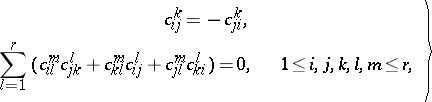
|
$\left. \begin{array} { c } { c _ { i j } ^ { k } = - c _ { j i } ^ { k } } \\ { \sum _ { l = 1 } ^ { r } ( c _ { i l } ^ { m } c _ { j k } ^ { l } + c _ { k l } ^ { m } c _ { i j } ^ { l } + c _ { j l } ^ { m } c _ { k i } ^ { l } ) = 0 , \quad 1 \leq i , j , k , l , m \leq r } \end{array} \right.$ | $$\left.\begin {array}c{c_{ij}^k=-c_{ji}^k},\\ {\displaystyle\sum _ {l=1}^r(c_{il}^mc_{jk}^l+c_{kl}^mc_{ij}^l+c_{jl}^mc_{ki}^l)=0,\quad 1 \leq i ,j,k,l,m\leq r,} \end {array} \right\}$$ | conf 0.085
l05876052.png (52) |
Maximal torus
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 91.(95.) | 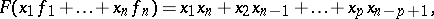
|
$F ( x _ { 1 } f _ { 1 } + \ldots + x _ { x } f _ { n } ) = x _ { 1 } x _ { n } + x _ { 2 } x _ { n } - 1 + \ldots + x _ { p } x _ { n } - p + 1$ | $$F(x_1f_1+\ldots +x_xf_n)=x_1x_n+x_2x_{n-1}+\ldots +x_px_{n-p+1},$$ | conf 0.198
m06301072.png (72) |
Non-Abelian cohomology
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 92.(114.)* | 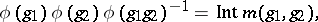
|
$\phi ( g _ { 1 } ) \phi ( g ) \phi ( g _ { 1 } g _ { 2 } ) ^ { - 1 } = \operatorname { Int } m ( g _ { 1 } , g _ { 2 } )$ | $$\phi (g_1)\phi (g_2)\phi (g_1g_2)^{-1}=\operatorname {Int}m(g_1,g_2),$$ | conf 0.443 F
n066900110.png (110) |
| 93.(90.)* | 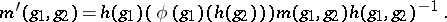
|
$( g _ { 1 } , g _ { 2 } ) = h ( g _ { 1 } ) ( \phi ( g _ { 1 } ) ( h ( g _ { 2 } ) ) ) m ( g _ { 1 } , g _ { 2 } ) h ( g _ { 1 } , g _ { 2 } ) ^ { - 1 }$ | $$m'(g_1,g_2)=h(g_1)(\phi (g_1)(h(g_2)))m(g_1,g_2)h(g_1,g_2)^{-1}.$$ | conf 0.764 F
n066900118.png (118) |
| 94.(44.) | 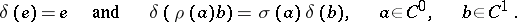
|
$\delta ( e ) = e \quad \text { and } \quad \delta ( \rho ( a ) b ) = \sigma ( a ) \delta ( b ) , \quad \alpha \in C ^ { 0 } , \quad b \in C ^ { 1 }$ | $$\delta (e)=e\quad \;\text{and }\quad \delta (\rho (a)b)=\sigma (a)\delta (b),\quad \alpha \in C ^0,\quad b \in C ^1,$$ | conf 0.400
n06690016.png (16) |
| 95.(60.)* | 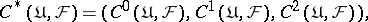
|
$C ^ { * } ( \mathfrak { U } , F ) = ( C ^ { 0 } ( \mathfrak { U } , F ) , C ^ { 1 } ( \mathfrak { U } , F ) , C ^ { 2 } ( \mathfrak { U } , F ) )$ | $$C^{*}(\mathfrak U,{\cal F})=(C^0(\mathfrak U,{\cal F}),C^1(\mathfrak U,{\cal F}),C^2(\mathfrak U,{\cal F})),$$ | conf 0.205 F
n06690028.png (28) |
Picard scheme
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 96.(39.)* | 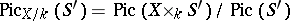
|
$\operatorname { Pic } _ { X / k } ( S ^ { \prime } ) = \operatorname { Fic } ( X \times k S ^ { \prime } ) / \operatorname { Fic } ( S ^ { \prime } )$ | $$\operatorname {Pic}_{X/k}(S^{\prime })=\operatorname {Pic}(X\times_k S ^{\prime })/\operatorname {Pic}(S^{\prime })$$ | conf 0.345 F +
p07267025.png (25) |
Principal analytic fibration
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 97.(100.)* | 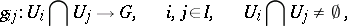
|
$g j : U _ { i } \cap U _ { j } \rightarrow G , \quad i , j \in I , \quad U _ { i } \cap U _ { j } \neq \emptyset$ | $$g_j:U_i\cap U _ j\rightarrow G ,\quad i ,j\in I ,\quad U _ i\cap U _ j\neq \emptyset,$$ | conf 0.184 F
p07464025.png (25) |
Quantum groups
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 98.(101.) | 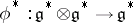
|
$\phi ^ { * } : \mathfrak { g } ^ { * } \otimes \mathfrak { g } ^ { * } \rightarrow \mathfrak { g } ^ { * }$ | $$\phi ^{*}:\mathfrak g^{*}\otimes \mathfrak g^{*}\rightarrow \mathfrak g^{*}$$ | conf 0.837
q07631062.png (62) |
| 99.(108.) | 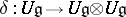
|
$\delta : U _ { \mathfrak { g } } \rightarrow U _ { \mathfrak { g } } \otimes U _ { \mathfrak { g } }$ | $$\delta :U_{\mathfrak g}\rightarrow U _ {\mathfrak g}\otimes U _ {\mathfrak g}$$ | conf 0.648
q07631071.png (71) |
| 100.(56.)* | 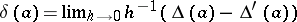
|
$\delta ( \alpha ) = \operatorname { lim } _ { h \rightarrow 0 } h ^ { - 1 } ( \Delta ( a ) - \Delta ^ { \prime } ( \alpha ) )$ | $$\delta (\alpha )=\operatorname {lim}_{h\rightarrow 0 }h^{-1}(\Delta (a)-\Delta ^{\prime }(\alpha ))$$ | conf 0.304 F
q07631072.png (72) |
| 101.(129.)* | 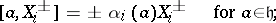
|
$[ \alpha , X _ { i } ^ { \pm } ] = \pm \alpha _ { i } ( \alpha ) X _ { i } ^ { \pm } \quad \text { for } a$ | $$[\alpha ,X_i^{\pm }]=\pm \alpha _ i(\alpha )X_i^{\pm }\quad \text{for }a\in \mathfrak h;$$ | conf 0.544 F
q07631088.png (88) |
| 102.(128.) | 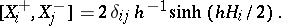
|
$[ X _ { i } ^ { + } , X _ { j } ^ { - } ] = 2 \delta _ { i j } h ^ { - 1 } \operatorname { sinh } ( h H _ { i } / 2 )$ | $$[X_i^{+},X_j^{-}]=2\delta _ {ij}h^{-1}\operatorname {sinh}(hH_i/2).$$ | conf 0.893
q07631089.png (89) |
| 103.(20.) | 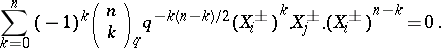
|
$\sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) q ^ { - k ( n - k ) / 2 } ( X _ { i } ^ { \pm } ) ^ { k } X _ { j } ^ { \pm } \cdot ( X _ { i } ^ { \pm } ) ^ { n - k } = 0$ | $$\sum _ {k=0}^n(-1)^k\left(\begin {array}ln\\ k \end {array} \right)q^{-k(n-k)/2}(X_i^{\pm })^kX_j^{\pm }\cdot (X_i^{\pm })^{n-k}=0.$$ | conf 0.055
q07631092.png (92) |
| 104.(30.) | 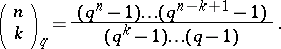
|
$\left( \begin{array} { l } { n } \\ { k } \end{array} \right) _ { q } = \frac { ( q ^ { n } - 1 ) \ldots ( q ^ { n - k + 1 } - 1 ) } { ( q ^ { k } - 1 ) \ldots ( q - 1 ) }$ | $$\left( \begin {array}ln\\ k \end {array} \right)_q=\frac {(q^n-1)\ldots (q^{n-k+1}-1)}{(q^k-1)\ldots (q-1)} .$$ | conf 0.443
q07631095.png (95) |
| 105.(21.)* | 
|
$\Delta ( X _ { i } ^ { \pm } ) = X _ { i } ^ { \pm } \bigotimes \operatorname { exp } ( \frac { h H _ { i } } { 4 } ) + \operatorname { exp } ( \frac { - h H _ { i } } { 4 } ) \otimes x _ { i } ^ { \pm }$ | $$\Delta (X_i^{\pm })=X_i^{\pm }\otimes \operatorname {exp}(\frac {hH_i}4)+\operatorname {exp}(\frac {-hH_i}4)\otimes X _ i^{\pm }.$$ | conf 0.212 F
q07631099.png (99) |
Rational representation
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 106.(91.) | 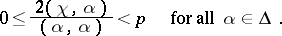
|
$0 \leq \frac { 2 ( \chi , \alpha ) } { ( \alpha , \alpha ) } < p \quad \text { for all } \alpha \in \Delta$ | $$0\leq \frac {2(\chi ,\alpha )}{(\alpha ,\alpha )}<p\quad \text{for all }\alpha \in \Delta.$$ | conf 0.879
r077630100.png (100) |
| 107.(135.) | 
|
$\phi _ { 0 } \bigotimes \phi _ { 1 } ^ { Fr } \otimes \ldots \otimes \phi _ { d } ^ { FF ^ { d } }$ | $$\phi _ 0\otimes \phi _ 1^{Fr}\otimes \ldots \otimes \phi _ d^{{Fr}^d},$$ | conf 0.136
r077630104.png (104) |
| 108.(45.)* | 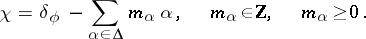
|
$\chi = \delta _ { \phi } - \sum _ { \alpha \in \Delta } m _ { \alpha } \alpha , \quad m _ { \alpha } \in Z , \quad m _ { \alpha } \geq 0$ | $$\chi =\delta _ {\phi }-\sum _ {\alpha \in \Delta }m_{\alpha }\alpha ,\quad m _ {\alpha }\in Z ,\quad m _ {\alpha }\geq 0.$$ | conf 0.862 F
r07763055.png (55) |
Singular point
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 109.(31.) | 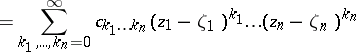
|
$\sum _ { k _ { 1 } , \ldots , k _ { n } = 0 } ^ { \infty } c _ { k _ { 1 } \cdots k _ { n } } ( z _ { 1 } - \zeta _ { 1 } ) ^ { k _ { 1 } } \ldots ( z _ { n } - \zeta _ { n } ) ^ { k _ { n } }$ | $$\sum _ {k_1,\ldots ,k_n=0}^{\infty }c_{k_1\cdots k _ n}(z_1-\zeta _ 1)^{k_1}\ldots (z_n-\zeta _ n)^{k_n}$$ | conf 0.324
s085590225.png (225) |
| 110.(46.) | 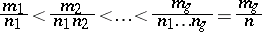
|
$\frac { m _ { 1 } } { n _ { 1 } } < \frac { m _ { 2 } } { n _ { 1 } n _ { 2 } } < \ldots < \frac { m _ { g } } { n _ { 1 } \ldots n _ { g } } = \frac { m _ { g } } { n }$ | $$\frac {m_1}{n_1}<\frac {m_2}{n_1n_2}<\ldots <\frac {m_g}{n_1\ldots n _ g}=\frac {m_g}n$$ | conf 0.459
s085590404.png (404) |
| 111.(115.)* | 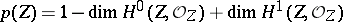
|
$p ( Z ) = 1 - \operatorname { dim } H ^ { 0 } ( Z , O _ { Z } ) + \operatorname { dim } H ^ { 1 } ( Z , O _ { Z } )$ | $$p(Z)=1-\operatorname {dim}H^0({\mathbf Z},{\cal O}_{\mathbf Z })+\operatorname {dim}H^1({\mathbf Z},{\cal O}_{\mathbf Z })$$ | conf 0.997 F
s085590429.png (429) |
| 112.(136.)* | 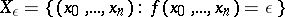
|
$X _ { \epsilon } = \{ ( x _ { 0 } , \ldots , x _ { x } ) : f ( x _ { 0 } , \ldots , x _ { x } ) = \epsilon \}$ | $$X_{\epsilon }=\{(x_0,\ldots ,x_x):f(x_0,\ldots ,x_x)=\epsilon \}$$ | conf 0.433 F
s085590440.png (440) |
| 113.(12.) | 
|
$= \left\{ \begin{array} { l l } { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } } & { \text { if } \mu = 2 k } \\ { ( x + \lambda ) ^ { 2 } \ldots ( x + k \lambda ) ^ { 2 } ( x + ( k + 1 ) \lambda ) } & { \text { if } \mu = 2 k + 1 } \end{array} \right.$ | $$=\left\{ \begin {array}{ll} {(x+\lambda )^2\ldots (x+k\lambda )^2} &{\text{ if }\mu =2k,}\\ {(x+\lambda )^2\ldots (x+k\lambda )^2(x+(k+1)\lambda )} &{\text{ if }\mu =2k+1,} \end {array} \right.$$ | conf 0.870
s085590458.png (458) |
| 114.(75.) | 
|
$( \frac { \partial F ( x , y , \lambda ) } { \partial x } , \frac { \partial F ( x , y , \lambda ) } { \partial y } )$ | $$\big(\frac {\partial F (x,y,\lambda )}{\partial x },\frac {\partial F (x,y,\lambda )}{\partial y }\big)$$ | conf 0.986
s085590482.png (482) |
| 115.(137.) | 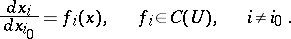
|
$\frac { d x _ { i } } { d x _ { i _ { 0 } } } = f _ { i } ( x ) , \quad f _ { i } \in C ( U ) , \quad i \neq i _ { 0 }$ | $$\frac {dx_i}{dx_{i_0}}=f_i(x),\quad f _ i\in C (U),\quad i \neq i _ 0.$$ | conf 0.594
s085590515.png (515) |
| 116.(142.)* | 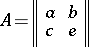
|
$A = \| \left. \begin{array} { l l } { \alpha } & { b } \\ { c } & { e } \end{array} \right. |$ | $$A=\left\| \begin {array}{ll} {\alpha } &b\\ c &e \end {array} \right\|$$ | conf 0.506 F
s085590527.png (527) |
| 117.(53.) | 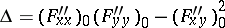
|
$\Delta = ( F _ { x x } ^ { \prime \prime } ) _ { 0 } ( F _ { y y } ^ { \prime \prime } ) _ { 0 } - ( F _ { x y } ^ { \prime \prime } ) _ { 0 } ^ { 2 }$ | $$\Delta =(F_{xx}^{\prime \prime })_0(F_{yy}^{\prime \prime })_0-(F_{xy}^{\prime \prime })_0^2$$ | conf 0.920
s085590634.png (634) |
| 118.(16.)* | 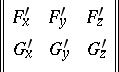
|
$\left| \begin{array} { l l l } { F _ { X } ^ { \prime } } & { F _ { y } ^ { \prime } } & { F _ { z } ^ { \prime } } \\ { G _ { \chi } ^ { \prime } } & { G _ { y } ^ { \prime } } & { G _ { Z } ^ { \prime } } \end{array} \right|$ | $$\left\| \begin {array}{lll} {F_x^{\prime }} &{F_y^{\prime }} &{F_z^{\prime }}\\ {G_x^{\prime }} &{G_y^{\prime }} &{G_Z^{\prime }} \end {array} \right\|$$ | conf 0.230 F
s085590645.png (645) |
| 119.(92.) | 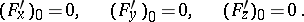
|
$( F _ { X } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { y } ^ { \prime } ) _ { 0 } = 0 , \quad ( F _ { z } ^ { \prime } ) _ { 0 } = 0$ | $$(F_x^{\prime })_0=0,\quad (F_y^{\prime })_0=0,\quad (F_z^{\prime })_0=0.$$ | conf 0.300
s085590653.png (653) |
Solv manifold
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 120.(138.) | 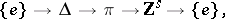
|
$\{ e \} \rightarrow \Delta \rightarrow \pi \rightarrow Z ^ { s } \rightarrow \{ e \}$ | $$\{e\}\rightarrow \Delta \rightarrow \pi \rightarrow {\mathbf Z}^s\rightarrow \{e\}$$ | conf 0.972
s08610054.png (54) |
Stability theorems in algebraic K-theory
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 121.(71.) | 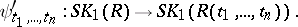
|
$\psi _ { t _ { 1 } , \ldots , t _ { R } } ^ { \prime } : S K _ { 1 } ( R ) \rightarrow S K _ { 1 } ( R ( t _ { 1 } , \ldots , t _ { n } ) )$ | $$\psi _ {t_1,\ldots ,t_n}^{\prime }:SK_1(R)\rightarrow S K _ 1(R(t_1,\ldots ,t_n)).$$ | conf 0.379
s08706033.png (33) |
Steinberg module
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 122.(130.) | 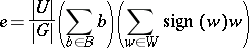
|
$e = \frac { | U | } { | G | } ( \sum _ { b \in B } b ) ( \sum _ { w \in W } \operatorname { sign } ( w ) w )$ | $$e=\frac {|U|}{|G|}\big(\sum _ {b\in B }b\big)\big(\sum _ {w\in W }\operatorname {sign}(w)w\big)$$ | conf 0.138
s13053016.png (16) |
Steinberg symbol
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 123.(24.)* | 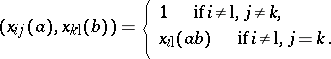
|
$( x _ { i j } ( a ) , x _ { k l } ( b ) ) = \left\{ \begin{array} { l l } { 1 } & { \text { if } i \neq 1 , j \neq k } \\ { x _ { 1 } ( a b ) } & { \text { if } i \neq 1 , j = k } \end{array} \right.$ | $$(x_{ij}(a),x_{kl}(b))=\left\{ \begin {array}{ll} 1 &{\text{ if }i\neq l ,j\neq k },\\ {x_{il}(ab)} &{\text{ if }i\neq l ,j=k}. \end {array} \right.$$ | conf 0.381 F
s13054017.png (17) |
Tilting theory
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 124.(84.) | 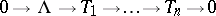
|
$0 \rightarrow \Lambda \rightarrow T _ { 1 } \rightarrow \ldots \rightarrow T _ { n } \rightarrow 0$ | $$0\rightarrow \Lambda \rightarrow T _ 1\rightarrow \ldots \rightarrow T _ n\rightarrow 0 $$ | conf 0.946
t130130105.png (105) |
Tits quadratic form
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 125.(18.) | 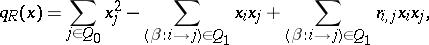
|
$q R ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { i } x _ { j } + \sum _ { \langle \beta : i \rightarrow j ) \in Q _ { 1 } } x _ { , j } x _ { i } x _ { j }$ | $$q_R(x)=\sum _ {j\in Q _ 0}x_j^2-\sum _ {\langle \beta :i\rightarrow j )\in Q _ 1}x_ix_j+\sum _ {\langle \beta :i\rightarrow j )\in Q _ 1}r_{i,j}x_ix_j,$$ | conf 0.112
t130140104.png (104) |
| 126.(40.) | 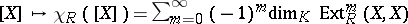
|
$[ X ] \mapsto \chi _ { R } ( [ X ] ) = \sum _ { m = 0 } ^ { \infty } ( - 1 ) ^ { m } \operatorname { dim } _ { K } \operatorname { Ext } _ { R } ^ { m } ( X , X )$ | $$[X]\mapsto \chi _ R([X])=\sum _ {m=0}^{\infty }(-1)^m\operatorname {dim}_K\operatorname {Ext}_R^m(X,X)$$ | conf 0.116
t130140118.png (118) |
| 127.(132.)* | 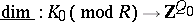
|
$\operatorname { dim } _ { 1 } : K _ { 0 } ( \operatorname { mod } R ) \rightarrow Z ^ { Q _ { 0 } }$ | $$\underline {\dim }:K_0(\operatorname {mod}R)\rightarrow {\mathbf Z}^{Q_0}$$ | conf 0.287 F
t130140119.png (119) |
| 128.(37.)* | 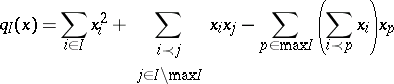
|
$q ( x ) = \sum _ { i \in I } x _ { i } ^ { 2 } + \sum _ { i \prec j } x _ { i } x _ { j } - \sum _ { p \in \operatorname { max } l } ( \sum _ { i \prec p } x _ { i } ) x _ { p }$ | $$q_I(x)=\sum _ {i\in I }x_i^2+\sum _ {i\prec j \atop j\in I\setminus {\rm max}I}x_ix_j-\sum _ {p\in \operatorname {max}I}\big(\sum _ {i\prec p }x_i\big)x_p$$ | conf 0.197 F
t130140140.png (140) |
| 129.(131.)* | 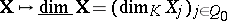
|
$X \mapsto \operatorname { dim } X = ( \operatorname { dim } _ { K } X _ { j } ) _ { j \in Q _ { 0 } }$ | $$X\mapsto \underline {\dim }X=(\operatorname {dim}_KX_j)_{j\in Q _ 0}$$ | conf 0.819 F
t13014044.png (44) |
| 130.(25. | 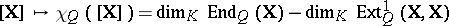
|
$[ X ] \mapsto \chi _ { Q } ( [ X ] ) = \operatorname { dim } _ { K } \operatorname { End } _ { Q } ( X ) - \operatorname { dim } _ { K } \operatorname { Ext } _ { Q } ^ { 1 } ( X , X )$ | $$[X]\mapsto \chi _ Q([X])=\operatorname {dim}_K\operatorname {End}_Q(X)-\operatorname {dim}_K\operatorname {Ext}_Q^1(X,X)$$ | conf 0.661
t13014048.png (48) |
| 131.(38.)* | 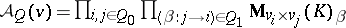
|
$A _ { Q } ( v ) = \prod _ { i , j \in Q _ { 0 } } \prod _ { \langle \beta : j \rightarrow i \rangle \in Q _ { 1 } } M _ { v _ { i } \times v _ { j } } ( K ) _ { \beta }$ | $$A_Q(v)=\prod _ {i,j\in Q _ 0}\prod _ {\langle \beta :j\rightarrow i \rangle \in Q _ 1}M_{v_i\times v _ j}(K)_{\beta }$$ | conf 0.481 F
t13014056.png (56) |
| 132.(139.)* | 
|
$\Phi ( x ) = \sum _ { j \in Q _ { 0 } } x _ { j } ^ { 2 } - \sum _ { i , j \in Q _ { 0 } } d _ { i j } x _ { i } x _ { j }$ | $$q_Q(x)=\sum _ {j\in Q _ 0}x_j^2-\sum _ {i,j\in Q _ 0}d_{ij}x_ix_j,$$ | conf 0.648 F
t1301406.png (6) |
Torus
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 133.(41.)* | 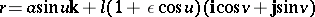
|
$r = \alpha \operatorname { sin } u k + l ( 1 + \epsilon \operatorname { cos } u ) ( i \operatorname { cos } v + j \operatorname { sin } v )$ | $$r=\alpha \operatorname {sin}u{\bf k}+l(1+\epsilon \operatorname {cos}u)({\bf i}\operatorname {cos}v+{\bf j}\operatorname {sin}v)$$ | conf 0.585 F
t0933502.png (2) |
| 134.(122.)* | 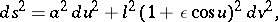
|
$d s ^ { 2 } = \alpha ^ { 2 } d u ^ { 2 } + l ^ { 2 } ( 1 + \epsilon \operatorname { cos } u ) ^ { 2 } d v ^ { 2 }$ | $$ds^2=\alpha ^2du^2+l^2(1+\epsilon \operatorname {cos}u)^2dv^2,$$ | conf 0.696 F
t0933507.png (7) |
Uniform distribution
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 135.(9.) | 
|
$u _ { 3 } ( x ) = \left\{ \begin{array} { l l } { \frac { x ^ { 2 } } { 2 } , } & { 0 \leq x < 1 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } ] } { 2 } , } & { 1 \leq x < 2 } \\ { \frac { [ x ^ { 2 } - 3 ( x - 1 ) ^ { 2 } + 3 ( x - 2 ) ^ { 2 } ] } { 2 } , } & { 2 \leq x < 3 } \\ { 0 , } & { x \notin [ 0,3 ] } \end{array} \right.$ | $$u_3(x)=\left\{ \begin {array}{ll} {\frac {x^2}2,} &{0\leq x <1,}\\ {\frac {[x^2-3(x-1)^2]}2,} &{1\leq x <2,}\\ {\frac {[x^2-3(x-1)^2+3(x-2)^2]}2,} &{2\leq x <3,}\\ {0,} &{x\notin [0,3].} \end {array} \right.$$ | conf 0.733
u09524027.png (27) |
| 136.(32.)* | 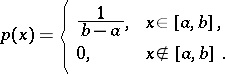
|
$p ( x ) = \left\{ \begin{array} { l l } { \frac { 1 } { b - \alpha } , } & { x \in [ \alpha , b ] } \\ { 0 , } & { x \notin [ \alpha , b ] } \end{array} \right.$ | $$p(x)=\left\{ \begin {array}{ll} {\frac 1{b-\alpha },} &{x\in [\alpha ,b],}\\ {0,} &{x\notin [\alpha ,b].} \end {array} \right.$$ | conf 0.681 F
u0952403.png (3) |
| 137.(34.) | 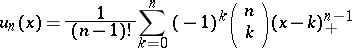
|
$u _ { n } ( x ) = \frac { 1 } { ( n - 1 ) ! } \sum _ { k = 0 } ^ { n } ( - 1 ) ^ { k } \left( \begin{array} { l } { n } \\ { k } \end{array} \right) ( x - k ) _ { + } ^ { n - 1 }$ | $$u_n(x)=\frac 1{(n-1)!}\sum _ {k=0}^n(-1)^k\left(\begin {array}ln\\ k \end {array} \right)(x-k)_{+}^{n-1}$$ | conf 0.569
u09524030.png (30) |
| 138.(109.) | 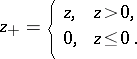
|
$z _ { + } = \left\{ \begin{array} { l l } { z , } & { z > 0 } \\ { 0 , } & { z \leq 0 } \end{array} \right.$ | $$z_{+}=\left\{ \begin {array}{ll} {z,} &{z>0}.\\ {0,} &{z\leq 0 }. \end {array} \right.$$ | conf 0.676
u09524034.png (34) |
| 139.(43.) | 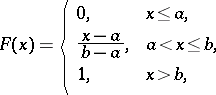
|
$F ( x ) = \left\{ \begin{array} { l l } { 0 , } & { x \leq a } \\ { \frac { x - a } { b - a } , } & { a < x \leq b } \\ { 1 , } & { x > b } \end{array} \right.$ | $$F(x)=\left\{ \begin {array}{ll} {0,} &{x\leq a },\\ {\frac {x-a}{b-a},} &{a<x\leq b },\\ {1,} &{x>b}, \end {array} \right.$$ | conf 0.468
u0952407.png (7) |
| 140.(47.) | 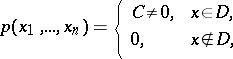
|
$p ( x _ { 1 } , \ldots , x _ { n } ) = \left\{ \begin{array} { l l } { C \neq 0 , } & { x \in D } \\ { 0 , } & { x \notin D } \end{array} \right.$ | $$p(x_1,\ldots ,x_n)=\left\{ \begin {array}{ll} {C\neq 0 ,} &{x\in D },\\ {0,} &{x\notin D }, \end {array} \right.$$ | conf 0.705
u09524072.png (72) |
Unipotent group
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 141.(143.) | 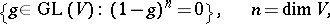
|
$\{ g \in \operatorname { GL } ( V ) : ( 1 - g ) ^ { n } = 0 \} , \quad n = \operatorname { dim } V$ | $$\{g\in \operatorname {GL}(V):(1-g)^n=0\},\quad n =\operatorname {dim}V,$$ | conf 0.287
u0954106.png (6) |
Weyl module
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 142.(51.) | 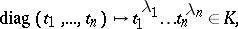
|
$\operatorname { diag } ( t _ { 1 } , \ldots , t _ { n } ) \mapsto t _ { 1 } ^ { \lambda _ { 1 } } \ldots t _ { n } ^ { \lambda _ { n } } \in K$ | $$\operatorname {diag}(t_1,\ldots ,t_n)\mapsto t _ 1^{\lambda _ 1}\ldots t _ n^{\lambda _ n}\in K,$$ | conf 0.507
w120090122.png (122) |
| 143.(54.)* | 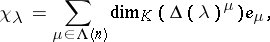
|
$\chi _ { \lambda } = \sum _ { \mu \in \Lambda ( n ) } \operatorname { dim } _ { K } ( \Delta ( \lambda ) ^ { \mu } ) _ { e _ { \mu } }$ | $$\chi _ {\lambda }=\sum _ {\mu \in \Lambda (n)}\operatorname {dim}_K(\Delta (\lambda )^{\mu })_{e_{\mu }},$$ | conf 0.461 F
w120090135.png (135) |
| 144.(110.) | 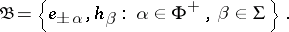
|
$\mathfrak { B } = \{ e _ { \pm } \alpha , h _ { \beta } : \alpha \in \Phi ^ { + } , \beta \in \Sigma \}$ | $$\mathfrak B=\{e_{\pm }\alpha ,h_{\beta }:\alpha \in \Phi ^{+},\beta \in \Sigma \}.$$ | conf 0.381
w120090259.png (259) |
| 145.(82.) | 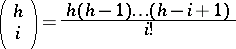
|
$\left( \begin{array} { c } { h } \\ { i } \end{array} \right) = \frac { h ( h - 1 ) \ldots ( h - i + 1 ) } { i ! }$ | $$\left( \begin {array}ch\\ i \end {array} \right)=\frac {h(h-1)\ldots (h-i+1)}{i!} $$ | conf 0.487
w120090342.png (342) |
| 146.(28.)* | 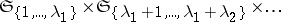
|
$\mathfrak { S } _ { \{ 1 , \ldots , \lambda _ { 1 } \} } \times \mathfrak { S } _ { \{ \lambda _ { 1 } + 1 , \ldots , \lambda _ { 1 } + \lambda _ { 2 } \} } \times$ | $$\mathfrak S_{\{1,\ldots ,\lambda _ 1\}}\times \mathfrak S_{\{\lambda _ 1+1,\ldots ,\lambda _ 1+\lambda _ 2\}}\times \dots $$ | conf 0.312 F
w12009095.png (95) |
| 147.(104.) | 
|
$\ldots \times \mathfrak { S } _ { \{ \lambda _ { 1 } + \ldots + \lambda _ { n - 1 } + 1 , \ldots , r \} }$ | $$\ldots \times \mathfrak S_{\{\lambda _ 1+\ldots +\lambda _ {n-1}+1,\ldots ,r\}},$$ | conf 0.259
w12009096.png (96) |
Witt vector
| Nr. | Image of png File | $\TeX$, automatically generated version | $\TeX$, manually corrected version | Confidence, F?
png file |
|---|---|---|---|---|
| 148.(87.)* | 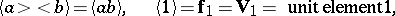
|
$\langle \alpha > < b \rangle = \langle \alpha b \rangle , \quad \langle 1 \rangle = f _ { 1 } = V _ { 1 } =$ | $$\langle \alpha ><b\rangle =\langle \alpha b \rangle ,\quad \langle {\bf 1}\rangle ={\bf f}_1={\bf V}_1=\text{ unit element}1,$$ | conf 0.351 F
w098100172.png (172) |
| 149.(123.)* | 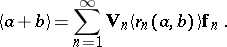
|
$\langle \alpha + b \rangle = \sum _ { n = 1 } ^ { \infty } V _ { n } \langle r _ { n } ( \alpha , b ) f$ | $$\langle \alpha +b\rangle =\sum _ {n=1}^{\infty }{\bf V}_n\langle r _ n(\alpha ,b){\bf f}_n.$$ | conf 0.143 F
w098100177.png (177) |
| 150.(102.) | 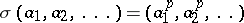
|
$\sigma ( \alpha _ { 1 } , \alpha _ { 2 } , \ldots ) = ( \alpha _ { 1 } ^ { p } , \alpha _ { 2 } ^ { p } , \ldots )$ | $$\sigma (\alpha _ 1,\alpha _ 2,\ldots )=(\alpha _ 1^p,\alpha _ 2^p,\ldots )$$ | conf 0.771
w098100190.png (190) |
Ulf Rehmann/Table of automatically generated TeX code. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ulf_Rehmann/Table_of_automatically_generated_TeX_code&oldid=44203