|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871301.png" /> be an associative ring with unit element. A sequence of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871302.png" /> is called left unimodular if the left ideal generated by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871303.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871304.png" />, is all of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871305.png" />.
| + | <!-- |
| | + | s0871301.png |
| | + | $#A+1 = 101 n = 2 |
| | + | $#C+1 = 101 : ~/encyclopedia/old_files/data/S087/S.0807130 Stable rank |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | The left stable rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871306.png" /> is the least integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871307.png" /> such that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871308.png" /> and left unimodular sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s0871309.png" /> there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713010.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713011.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713013.png" />, is also left unimodular.
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | The right stable rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713014.png" /> is defined analogously by replacing left with right everywhere. The left and right stable ranks are equal [[#References|[a1]]], cf. also, e.g., [[#References|[a2]]], §11.3, and both are therefore called the stable rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713015.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713016.png" />.
| + | Let $ R $ |
| | + | be an associative ring with unit element. A sequence of elements $ ( a _ {1} \dots a _ {n} ) $ |
| | + | is called left unimodular if the left ideal generated by the $ a _ {i} $, |
| | + | $ i= 1 \dots n $, |
| | + | is all of $ R $. |
| | | | |
| − | By writing a left unimodular sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713017.png" /> as a column, there is a natural left action of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713018.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713019.png" />, the set of all left unimodular sequences of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713020.png" />. The general linear rank, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713021.png" />, of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713022.png" /> is the least integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713023.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713024.png" /> acts transitively on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713025.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713026.png" />. This is equivalent to the property that all right stably-free modules of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713027.png" /> are free, [[#References|[a2]]].
| + | The left stable rank of $ R $ |
| | + | is the least integer $ n $ |
| | + | such that for each $ m> n $ |
| | + | and left unimodular sequence $ ( a _ {1} \dots a _ {m} ) $ |
| | + | there are $ r _ {1} \dots r _ {m-} 1 $ |
| | + | such that $ ( a _ {1} ^ \prime \dots a _ {m-} 1 ^ \prime ) $ |
| | + | with $ a _ {i} ^ \prime = a _ {i} + r _ {i} a _ {m} $, |
| | + | $ i= 1 \dots m- 1 $, |
| | + | is also left unimodular. |
| | | | |
| − | Recall that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713028.png" /> is [[Stably free module|stably free]] if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713029.png" /> for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713030.png" />; the rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713031.png" /> is then defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713032.png" />. This is well-defined if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713033.png" /> has the invariant basis property (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713034.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713035.png" />). This property holds, e.g., if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713036.png" /> is commutative or right Noetherian.
| + | The right stable rank of $ R $ |
| | + | is defined analogously by replacing left with right everywhere. The left and right stable ranks are equal [[#References|[a1]]], cf. also, e.g., [[#References|[a2]]], §11.3, and both are therefore called the stable rank of $ R $, |
| | + | denoted by $ \textrm{ st.r. } ( R) $. |
| | | | |
| − | One has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713037.png" />, so that any stably-free module of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713038.png" /> is free.
| + | By writing a left unimodular sequence $ ( a _ {1} \dots a _ {n} ) $ |
| | + | as a column, there is a natural left action of $ \mathop{\rm GL} _ {n} ( R ) $ |
| | + | on $ U _ {c} ( n, R ) $, |
| | + | the set of all left unimodular sequences of length $ n $. |
| | + | The general linear rank, $ \mathop{\rm glr} ( R) $, |
| | + | of $ R $ |
| | + | is the least integer $ n $ |
| | + | such that $ \mathop{\rm GL} _ {m} ( R) $ |
| | + | acts transitively on $ U _ {c} ( m, R) $ |
| | + | for all $ m> n $. |
| | + | This is equivalent to the property that all right stably-free modules of rank $ \geq n $ |
| | + | are free, [[#References|[a2]]]. |
| | | | |
| − | For a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713039.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713040.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713041.png" />.
| + | Recall that $ P $ |
| | + | is [[Stably free module|stably free]] if $ P\oplus R ^ {n} \simeq R ^ {m} $ |
| | + | for some $ n, m $; |
| | + | the rank of $ P $ |
| | + | is then defined as $ m- n $. |
| | + | This is well-defined if $ R $ |
| | + | has the invariant basis property (i.e. $ R ^ {n} \simeq R ^ {m} $ |
| | + | if and only if $ n= m $). |
| | + | This property holds, e.g., if $ R $ |
| | + | is commutative or right Noetherian. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713042.png" /> be a field of transcendence degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713043.png" /> over its prime subfield <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713044.png" />. The Kronecker dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713045.png" /> is then defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713046.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713047.png" /> and as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713048.png" /> otherwise. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713049.png" /> Kronecker dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713050.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713051.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713052.png" /> is commutative of Krull dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713053.png" /> (cf. also [[Dimension|Dimension]] of an associative ring), then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713054.png" /> (Bass' theorem).
| + | One has $ \mathop{\rm glr} ( R) \leq \textrm{ st.r. } ( R) $, |
| | + | so that any stably-free module of rank $ \geq \textrm{ st.r. } ( R) $ |
| | + | is free. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713055.png" /> be a topological space, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713056.png" /> a metric space and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713057.png" /> a continuous mapping. A point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713058.png" /> is a stable value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713059.png" /> if it is in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713060.png" /> and if there is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713061.png" /> such that for every continuous mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713062.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713063.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713064.png" /> it is still true that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713065.png" />. The mapping dimension of a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713067.png" />, is the largest integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713068.png" /> for which there exists a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713069.png" /> for which the origin is a stable value. (If no such <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713070.png" /> exists, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713071.png" /> is set equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713072.png" />.) For nice spaces, e.g., metrizable, separable, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713073.png" />, this concept of dimension coincides with other notions of dimension, such as inductive dimension, [[#References|[a5]]], Chapt. VI, §1 (cf. [[Dimension theory|Dimension theory]]). It always coincides with the notion of dimension defined by essential mappings (cf. [[Dimension theory|Dimension theory]]), [[#References|[a5]]], Chapt. VI, §3.
| + | For a field $ k $ |
| | + | one has $ \mathop{\rm glr} ( k[ X _ {1} \dots X _ {n} ])= 1 $ |
| | + | for all $ n $. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713074.png" /> be the ring of real-valued continuous functions on a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713075.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713076.png" /> the subring of bounded functions. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713077.png" /> (Vaserstein's theorem). | + | Let $ k $ |
| | + | be a field of transcendence degree $ t $ |
| | + | over its prime subfield $ k _ {0} $. |
| | + | The Kronecker dimension of $ k $ |
| | + | is then defined as $ t+ 1 $ |
| | + | if $ \mathop{\rm char} k= 0 $ |
| | + | and as $ t $ |
| | + | otherwise. For $ n\leq $ |
| | + | Kronecker dimension of $ k $, |
| | + | $ \textrm{ st.r. } ( k[ X _ {1} \dots X _ {n} ]) = n+ 1 $. |
| | + | If $ R $ |
| | + | is commutative of Krull dimension $ m< \infty $( |
| | + | cf. also [[Dimension|Dimension]] of an associative ring), then $ \textrm{ st.r. } ( R[ X _ {1} \dots X _ {n} ]) \leq m+ n+ 1 $( |
| | + | Bass' theorem). |
| | | | |
| − | Both Bass' and Vaserstein's theorem indicate that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713078.png" /> is a good dimension concept for rings.
| + | Let $ X $ |
| | + | be a topological space, $ Y $ |
| | + | a metric space and $ f: X \rightarrow Y $ |
| | + | a continuous mapping. A point $ y \in Y $ |
| | + | is a stable value of $ f $ |
| | + | if it is in $ f( X) $ |
| | + | and if there is an $ \epsilon $ |
| | + | such that for every continuous mapping $ g: X \rightarrow Y $ |
| | + | with $ \| f( x)- g( x) \| < \epsilon $ |
| | + | for all $ x \in X $ |
| | + | it is still true that $ y \in g( X) $. |
| | + | The mapping dimension of a topological space $ X $, |
| | + | $ d( X) $, |
| | + | is the largest integer $ d $ |
| | + | for which there exists a mapping $ X \rightarrow \mathbf R ^ {d} $ |
| | + | for which the origin is a stable value. (If no such $ d $ |
| | + | exists, $ d( X) $ |
| | + | is set equal to $ \infty $.) |
| | + | For nice spaces, e.g., metrizable, separable, $ X $, |
| | + | this concept of dimension coincides with other notions of dimension, such as inductive dimension, [[#References|[a5]]], Chapt. VI, §1 (cf. [[Dimension theory|Dimension theory]]). It always coincides with the notion of dimension defined by essential mappings (cf. [[Dimension theory|Dimension theory]]), [[#References|[a5]]], Chapt. VI, §3. |
| | | | |
| − | More generally, the stable rank is defined for subrings and ideals of an associative ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713079.png" /> with unit.
| + | Let $ C( X) $ |
| | + | be the ring of real-valued continuous functions on a topological space $ X $ |
| | + | and $ C _ {b} ( X) \subset C( X) $ |
| | + | the subring of bounded functions. Then $ \textrm{ st.r. } ( C( X)) = \textrm{ st.r. } ( C _ {b} ( X))= d( X)+ 1 $( |
| | + | Vaserstein's theorem). |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713080.png" /> be an associative ring with unit, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713081.png" /> be a subring (possibly without unit) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713082.png" />. A sequence of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713083.png" /> is left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713085.png" />-unimodular if it is left unimodular (in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713086.png" />) and, moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713087.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713088.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713089.png" />. The stable rank of the subring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713090.png" /> is the least number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713091.png" /> such that for each left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713092.png" />-unimodular sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713093.png" /> of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713094.png" /> there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713095.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713096.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713097.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713098.png" />, is a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s08713099.png" />-unimodular sequence of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s087130100.png" />. (Such a property is referred to as a stable range condition, cf., e.g., [[#References|[a4]]]). The stable rank of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s087130101.png" /> does not depend on the ambient ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s087130102.png" />. Again it is true that the notion of stable rank is left/right symmetric, [[#References|[a1]]].
| + | Both Bass' and Vaserstein's theorem indicate that $ \textrm{ st.r. } ( R) - 1 $ |
| | + | is a good dimension concept for rings. |
| | + | |
| | + | More generally, the stable rank is defined for subrings and ideals of an associative ring $ R $ |
| | + | with unit. |
| | + | |
| | + | Let $ R $ |
| | + | be an associative ring with unit, and let $ \mathfrak q $ |
| | + | be a subring (possibly without unit) of $ R $. |
| | + | A sequence of elements $ ( a _ {1} \dots a _ {n} ) $ |
| | + | is left $ \mathfrak q $- |
| | + | unimodular if it is left unimodular (in $ R $) |
| | + | and, moreover, $ a _ {1} - 1 \in \mathfrak q $, |
| | + | $ a _ {i} \in \mathfrak q $, |
| | + | $ i= 2 \dots n $. |
| | + | The stable rank of the subring $ \mathfrak q $ |
| | + | is the least number $ n $ |
| | + | such that for each left $ \mathfrak q $- |
| | + | unimodular sequence $ ( a _ {1} \dots a _ {m} ) $ |
| | + | of length $ m> n $ |
| | + | there are $ q _ {i} \in \mathfrak q $, |
| | + | $ i= 1 \dots m- 1 $, |
| | + | such that $ ( a _ {1} ^ \prime \dots a _ {m-} 1 ^ \prime ) $, |
| | + | with $ a _ {i} ^ \prime = a _ {i} + q _ {i} a _ {m} $, |
| | + | is a left $ \mathfrak q $- |
| | + | unimodular sequence of length $ m- 1 $. |
| | + | (Such a property is referred to as a stable range condition, cf., e.g., [[#References|[a4]]]). The stable rank of $ \mathfrak q $ |
| | + | does not depend on the ambient ring $ R $. |
| | + | Again it is true that the notion of stable rank is left/right symmetric, [[#References|[a1]]]. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.N. Vaserstein, "Stable ranks of rings and dimensionality of topological spaces" ''Funct. Anal. Appl.'' , '''5''' (1971) pp. 102–110 ''Funkts. Anal. i Prilozhen.'' , '''5''' : 2 (1970) pp. 17–27</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) {{MR|934572}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.J. Hahn, O.T. O'Meara, "The classical groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s087130103.png" />-theory" , Springer (1981) pp. §4.1 {{MR|1007302}} {{MR|0842441}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Bass, "Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s087130104.png" />-theory" , Benjamin (1968) pp. Chapt. V, §3 {{MR|249491}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948)</TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.N. Vaserstein, "Stable ranks of rings and dimensionality of topological spaces" ''Funct. Anal. Appl.'' , '''5''' (1971) pp. 102–110 ''Funkts. Anal. i Prilozhen.'' , '''5''' : 2 (1970) pp. 17–27</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) {{MR|934572}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.J. Hahn, O.T. O'Meara, "The classical groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s087130103.png" />-theory" , Springer (1981) pp. §4.1 {{MR|1007302}} {{MR|0842441}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Bass, "Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087130/s087130104.png" />-theory" , Benjamin (1968) pp. Chapt. V, §3 {{MR|249491}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948)</TD></TR></table> |
Let $ R $
be an associative ring with unit element. A sequence of elements $ ( a _ {1} \dots a _ {n} ) $
is called left unimodular if the left ideal generated by the $ a _ {i} $,
$ i= 1 \dots n $,
is all of $ R $.
The left stable rank of $ R $
is the least integer $ n $
such that for each $ m> n $
and left unimodular sequence $ ( a _ {1} \dots a _ {m} ) $
there are $ r _ {1} \dots r _ {m-} 1 $
such that $ ( a _ {1} ^ \prime \dots a _ {m-} 1 ^ \prime ) $
with $ a _ {i} ^ \prime = a _ {i} + r _ {i} a _ {m} $,
$ i= 1 \dots m- 1 $,
is also left unimodular.
The right stable rank of $ R $
is defined analogously by replacing left with right everywhere. The left and right stable ranks are equal [a1], cf. also, e.g., [a2], §11.3, and both are therefore called the stable rank of $ R $,
denoted by $ \textrm{ st.r. } ( R) $.
By writing a left unimodular sequence $ ( a _ {1} \dots a _ {n} ) $
as a column, there is a natural left action of $ \mathop{\rm GL} _ {n} ( R ) $
on $ U _ {c} ( n, R ) $,
the set of all left unimodular sequences of length $ n $.
The general linear rank, $ \mathop{\rm glr} ( R) $,
of $ R $
is the least integer $ n $
such that $ \mathop{\rm GL} _ {m} ( R) $
acts transitively on $ U _ {c} ( m, R) $
for all $ m> n $.
This is equivalent to the property that all right stably-free modules of rank $ \geq n $
are free, [a2].
Recall that $ P $
is stably free if $ P\oplus R ^ {n} \simeq R ^ {m} $
for some $ n, m $;
the rank of $ P $
is then defined as $ m- n $.
This is well-defined if $ R $
has the invariant basis property (i.e. $ R ^ {n} \simeq R ^ {m} $
if and only if $ n= m $).
This property holds, e.g., if $ R $
is commutative or right Noetherian.
One has $ \mathop{\rm glr} ( R) \leq \textrm{ st.r. } ( R) $,
so that any stably-free module of rank $ \geq \textrm{ st.r. } ( R) $
is free.
For a field $ k $
one has $ \mathop{\rm glr} ( k[ X _ {1} \dots X _ {n} ])= 1 $
for all $ n $.
Let $ k $
be a field of transcendence degree $ t $
over its prime subfield $ k _ {0} $.
The Kronecker dimension of $ k $
is then defined as $ t+ 1 $
if $ \mathop{\rm char} k= 0 $
and as $ t $
otherwise. For $ n\leq $
Kronecker dimension of $ k $,
$ \textrm{ st.r. } ( k[ X _ {1} \dots X _ {n} ]) = n+ 1 $.
If $ R $
is commutative of Krull dimension $ m< \infty $(
cf. also Dimension of an associative ring), then $ \textrm{ st.r. } ( R[ X _ {1} \dots X _ {n} ]) \leq m+ n+ 1 $(
Bass' theorem).
Let $ X $
be a topological space, $ Y $
a metric space and $ f: X \rightarrow Y $
a continuous mapping. A point $ y \in Y $
is a stable value of $ f $
if it is in $ f( X) $
and if there is an $ \epsilon $
such that for every continuous mapping $ g: X \rightarrow Y $
with $ \| f( x)- g( x) \| < \epsilon $
for all $ x \in X $
it is still true that $ y \in g( X) $.
The mapping dimension of a topological space $ X $,
$ d( X) $,
is the largest integer $ d $
for which there exists a mapping $ X \rightarrow \mathbf R ^ {d} $
for which the origin is a stable value. (If no such $ d $
exists, $ d( X) $
is set equal to $ \infty $.)
For nice spaces, e.g., metrizable, separable, $ X $,
this concept of dimension coincides with other notions of dimension, such as inductive dimension, [a5], Chapt. VI, §1 (cf. Dimension theory). It always coincides with the notion of dimension defined by essential mappings (cf. Dimension theory), [a5], Chapt. VI, §3.
Let $ C( X) $
be the ring of real-valued continuous functions on a topological space $ X $
and $ C _ {b} ( X) \subset C( X) $
the subring of bounded functions. Then $ \textrm{ st.r. } ( C( X)) = \textrm{ st.r. } ( C _ {b} ( X))= d( X)+ 1 $(
Vaserstein's theorem).
Both Bass' and Vaserstein's theorem indicate that $ \textrm{ st.r. } ( R) - 1 $
is a good dimension concept for rings.
More generally, the stable rank is defined for subrings and ideals of an associative ring $ R $
with unit.
Let $ R $
be an associative ring with unit, and let $ \mathfrak q $
be a subring (possibly without unit) of $ R $.
A sequence of elements $ ( a _ {1} \dots a _ {n} ) $
is left $ \mathfrak q $-
unimodular if it is left unimodular (in $ R $)
and, moreover, $ a _ {1} - 1 \in \mathfrak q $,
$ a _ {i} \in \mathfrak q $,
$ i= 2 \dots n $.
The stable rank of the subring $ \mathfrak q $
is the least number $ n $
such that for each left $ \mathfrak q $-
unimodular sequence $ ( a _ {1} \dots a _ {m} ) $
of length $ m> n $
there are $ q _ {i} \in \mathfrak q $,
$ i= 1 \dots m- 1 $,
such that $ ( a _ {1} ^ \prime \dots a _ {m-} 1 ^ \prime ) $,
with $ a _ {i} ^ \prime = a _ {i} + q _ {i} a _ {m} $,
is a left $ \mathfrak q $-
unimodular sequence of length $ m- 1 $.
(Such a property is referred to as a stable range condition, cf., e.g., [a4]). The stable rank of $ \mathfrak q $
does not depend on the ambient ring $ R $.
Again it is true that the notion of stable rank is left/right symmetric, [a1].
References
| [a1] | L.N. Vaserstein, "Stable ranks of rings and dimensionality of topological spaces" Funct. Anal. Appl. , 5 (1971) pp. 102–110 Funkts. Anal. i Prilozhen. , 5 : 2 (1970) pp. 17–27 |
| [a2] | J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) MR934572 |
| [a3] | A.J. Hahn, O.T. O'Meara, "The classical groups and 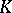 -theory" , Springer (1981) pp. §4.1 MR1007302 MR0842441 -theory" , Springer (1981) pp. §4.1 MR1007302 MR0842441 |
| [a4] | H. Bass, "Algebraic 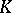 -theory" , Benjamin (1968) pp. Chapt. V, §3 MR249491 -theory" , Benjamin (1968) pp. Chapt. V, §3 MR249491 |
| [a5] | W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
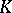 -theory" , Springer (1981) pp. §4.1 MR1007302 MR0842441
-theory" , Springer (1981) pp. §4.1 MR1007302 MR0842441 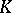 -theory" , Benjamin (1968) pp. Chapt. V, §3 MR249491
-theory" , Benjamin (1968) pp. Chapt. V, §3 MR249491