|
|
| (2 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| − | {{TEX|wanted}} | + | {{TEX|done}} |
| | | | |
| | ''Lagrange finite-increments formula'' | | ''Lagrange finite-increments formula'' |
| | | | |
| − | A formula expressing the increment of a function in terms of the value of its derivative at an intermediate point. If a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403001.png" /> is continuous on an interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403002.png" /> on the real axis and is differentiable at the interior points of it, then
| + | <span id="Fig1"> |
| − | | + | [[File:Finite-increments-formula-1.gif| right| frame| Figure 1. Given the [[chord]] of the graph of the function $f$ with end points $(a,f(a))$, $(b,f(b))$, then there exists a point $\xi$, $a<\xi<b$, such that the [[Tangent line|tangent]] to the graph of the function at the point $(\xi,f(\xi))$ is parallel to the chord.]] |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403003.png" /></td> </tr></table> | + | </span> |
| | | | |
| | + | A formula expressing the increment of a function in terms of the value of its derivative at an intermediate point. If a function $f$ is continuous on an interval $[a,b]$ on the real axis and is differentiable at the interior points of it, then |
| | + | \begin{equation} |
| | + | f(b)-f(a)=f'(\xi)(b-a),\quad a<\xi<b. |
| | + | \end{equation} |
| | The finite-increments formula can also be written in the form | | The finite-increments formula can also be written in the form |
| | + | \begin{equation} |
| | + | f(x+\Delta x)-f(x)=f'(x+\theta\Delta x)\Delta x,\quad 0<\theta<1. |
| | + | \end{equation} |
| | + | The geometric meaning of the finite-increments formula is illustrated in [[#Fig1|Figure 1]]. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403004.png" /></td> </tr></table>
| + | The finite-increments formula can be generalized to functions of several variables: If a function $f$ is differentiable at each point of a [[convex domain]] $G$ in an $n$-dimensional [[Euclidean space]], then there exists for each pair of points $x=(x_1,\dots,x_n)\in G$, $x+\Delta x=(x_1+\Delta x_1,\dots,x_n+\Delta x_n)\in G$ a point $\xi=(\xi_1,\ldots,\xi_n)$ lying on the segment joining $x$ and $x+\Delta x$ and such that |
| | + | \begin{equation} |
| | + | f(x+\Delta x)-f(x)=\sum_{i=1}^n\dfrac{\partial f(\xi)}{\partial x_i}\Delta x_i,\quad \xi_i=x_i+\theta\Delta x_i,\quad 0<\theta<1,\quad i=1,\ldots,n. |
| | + | \end{equation} |
| | | | |
| − | The geometric meaning of the finite-increments formula is: Given the chord of the graph of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403005.png" /> with end points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403006.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403007.png" />, then there exists a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403008.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f0403009.png" />, such that the tangent to the graph of the function at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030010.png" /> is parallel to the chord (see Fig.).
| |
| − |
| |
| − | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/f040300a.gif" />
| |
| − |
| |
| − | Figure: f040300a
| |
| − |
| |
| − | The finite-increments formula can be generalized to functions of several variables: If a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030011.png" /> is differentiable at each point of a convex domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030012.png" /> in an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030013.png" />-dimensional Euclidean space, then there exists for each pair of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030015.png" /> a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030016.png" /> lying on the segment joining <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030018.png" /> and such that
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030019.png" /></td> </tr></table>
| |
| − |
| |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030020.png" /></td> </tr></table>
| |
| | | | |
| | | | |
| | + | ====Comments==== |
| | | | |
| − | ====Comments====
| + | This formula is usually called the mean-value theorem (for derivatives). It is a statement for real-valued functions only; consider, e.g., $f(x)=e^{ix}$. |
| − | This formula is usually called the mean-value theorem (for derivatives). It is a statement for real-valued functions only; consider, e.g., <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040300/f04030021.png" />. | |
Latest revision as of 08:41, 28 April 2016
Lagrange finite-increments formula
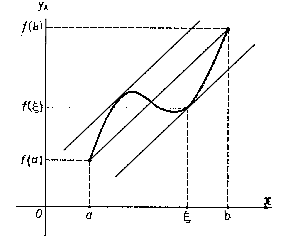
Figure 1. Given the
chord of the graph of the function $f$ with end points $(a,f(a))$, $(b,f(b))$, then there exists a point $\xi$, $a<\xi<b$, such that the
tangent to the graph of the function at the point $(\xi,f(\xi))$ is parallel to the chord.
A formula expressing the increment of a function in terms of the value of its derivative at an intermediate point. If a function $f$ is continuous on an interval $[a,b]$ on the real axis and is differentiable at the interior points of it, then
\begin{equation}
f(b)-f(a)=f'(\xi)(b-a),\quad a<\xi<b.
\end{equation}
The finite-increments formula can also be written in the form
\begin{equation}
f(x+\Delta x)-f(x)=f'(x+\theta\Delta x)\Delta x,\quad 0<\theta<1.
\end{equation}
The geometric meaning of the finite-increments formula is illustrated in Figure 1.
The finite-increments formula can be generalized to functions of several variables: If a function $f$ is differentiable at each point of a convex domain $G$ in an $n$-dimensional Euclidean space, then there exists for each pair of points $x=(x_1,\dots,x_n)\in G$, $x+\Delta x=(x_1+\Delta x_1,\dots,x_n+\Delta x_n)\in G$ a point $\xi=(\xi_1,\ldots,\xi_n)$ lying on the segment joining $x$ and $x+\Delta x$ and such that
\begin{equation}
f(x+\Delta x)-f(x)=\sum_{i=1}^n\dfrac{\partial f(\xi)}{\partial x_i}\Delta x_i,\quad \xi_i=x_i+\theta\Delta x_i,\quad 0<\theta<1,\quad i=1,\ldots,n.
\end{equation}
This formula is usually called the mean-value theorem (for derivatives). It is a statement for real-valued functions only; consider, e.g., $f(x)=e^{ix}$.
How to Cite This Entry:
Finite-increments formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Finite-increments_formula&oldid=29419
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article