Difference between revisions of "Index formulas"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | i0506501.png | ||
| + | $#A+1 = 377 n = 10 | ||
| + | $#C+1 = 377 : ~/encyclopedia/old_files/data/I050/I.0500650 Index formulas | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
Relations between analytic and topological invariants of operators of a certain class. More precisely, index formulas establish a relation between the analytic index of a linear operator | Relations between analytic and topological invariants of operators of a certain class. More precisely, index formulas establish a relation between the analytic index of a linear operator | ||
| − | + | $$ | |
| + | D : L _ {0} \rightarrow L _ {1} $$ | ||
| − | ( | + | ( $ L _ {0} , L _ {1} $ |
| + | are topological vector spaces), defined by the formula | ||
| − | + | $$ | |
| + | i _ {a} ( D) = \ | ||
| + | \mathop{\rm dim} \mathop{\rm Ker} D | ||
| + | - \mathop{\rm dim} \mathop{\rm Coker} D \in \mathbf Z | ||
| + | $$ | ||
| − | and measuring in this way the | + | and measuring in this way the "difference" between the defective subspaces of $ D $( |
| + | namely, the kernel $ \mathop{\rm Ker} D = D ^ {-} 1 ( 0) $ | ||
| + | and its cokernel $ \mathop{\rm Coker} D = L _ {1} / D ( L _ {0} ) $), | ||
| + | and a topological index, namely some topological characteristic of the operator $ D $ | ||
| + | and the spaces $ L _ {0} $, | ||
| + | $ L _ {1} $. | ||
| + | For a general elliptic differential operator on a closed manifold, the problem of finding index formulas was posed towards the end of the 1950's [[#References|[1]]] and solved in 1963 (see [[#References|[2]]]), although special forms of index formulas were known even earlier, for example, the [[Gauss–Bonnet theorem|Gauss–Bonnet theorem]] and its multi-dimensional variants. Subsequently a number of generalizations of index formulas were obtained for objects of a more complex nature; in these cases, instead of the index, which is an integer, arbitrary complex numbers and more general objects (e.g. functions) may feature. | ||
==Elementary index formulas.== | ==Elementary index formulas.== | ||
| + | 1) Let $ M $ | ||
| + | be the differentiable boundary of a bounded region $ \Omega \subset \mathbf R ^ {n+} 1 $ | ||
| + | and let $ A $ | ||
| + | be an elliptic pseudo-differential operator mapping the space $ C ^ \infty ( M , \mathbf C ^ {p} ) $ | ||
| + | of differentiable complex-valued vector functions on $ M $ | ||
| + | with values in $ \mathbf C ^ {p} $ | ||
| + | into itself. Let $ B( M) $ | ||
| + | be the manifold of tangent vectors to $ M $ | ||
| + | of length $ \leq 1 $, | ||
| + | oriented by means of the $ 2 n $- | ||
| + | form | ||
| + | |||
| + | $$ | ||
| + | ( d x ^ {1} \wedge d \xi _ {1} ) \wedge \dots | ||
| + | \wedge ( d x ^ {n} \wedge d \xi _ {n} ) , | ||
| + | $$ | ||
| + | |||
| + | where $ x ^ {1} \dots x ^ {n} $ | ||
| + | are local coordinates on $ M $, | ||
| + | $ \xi _ {1} \dots \xi _ {n} $ | ||
| + | are the corresponding coordinates in the tangent space, and let $ S ( M) $ | ||
| + | be the oriented boundary of $ B ( M) $ | ||
| + | formed by the unit tangent vectors. Since $ A $ | ||
| + | is elliptic, its symbol $ a $ | ||
| + | is a non-singular $ ( p \times p ) $- | ||
| + | matrix function on $ S ( M) $. | ||
| + | It turns out that the following Dynin–Fedosov formula holds for the index of $ A $[[#References|[7]]]: | ||
| + | |||
| + | $$ \tag{1 } | ||
| + | \mathop{\rm ind} A = \ | ||
| + | |||
| + | \frac{( - 1 ) ^ {n-} 1 ( n - 1 ) ! }{( 2 \pi i ) ^ {n} ( 2 n - 1 ) ! } | ||
| + | |||
| + | \int\limits _ {S ( M) } | ||
| + | \mathop{\rm Tr} ( a ^ {-} 1 d a ) ^ {\wedge ^ {2n-} 1 } , | ||
| + | $$ | ||
| − | 1) | + | where $ ( a ^ {-} 1 d a ) ^ {\wedge ^ {2n-} 1 } $ |
| + | is the exterior power of the matrix exterior form $ a ^ {-} 1 d a $ | ||
| + | and $ \mathop{\rm Tr} $ | ||
| + | denotes the trace of the $ ( p \times p ) $- | ||
| + | matrix form. In particular, if $ p < n $ | ||
| + | or if $ A $ | ||
| + | is a differential operator on an odd-dimensional manifold, then $ \mathop{\rm ind} A = 0 $( | ||
| + | this is not true, in general, for a pseudo-differential operator). | ||
| − | + | 2) Let $ A $ | |
| + | be an elliptic differential operator of the form | ||
| − | + | $$ | |
| + | A = \sum _ | ||
| + | {| \alpha | \leq m } | ||
| + | A _ \alpha ( x) | ||
| + | \left ( | ||
| + | \frac{1}{i} | ||
| − | + | \frac \partial {\partial x } | |
| − | + | \right ) ^ \alpha | |
| + | $$ | ||
| − | + | (where $ \alpha $ | |
| + | is a multi-index) in the space $ C ^ \infty ( \Omega ) $, | ||
| + | and let $ B _ {1} \dots B _ {m/2} $ | ||
| + | be boundary differential operators from $ C ^ \infty ( \Omega ) $ | ||
| + | into $ C ^ \infty ( M) $ | ||
| + | of the form | ||
| − | + | $$ | |
| + | B _ {j} = \sum _ | ||
| + | {| \alpha | \leq m _ {j} } | ||
| + | B _ {j \alpha } ( x) | ||
| + | \left ( | ||
| + | \frac{1}{i} | ||
| − | + | \frac \partial {\partial x } | |
| − | + | \right ) ^ \alpha . | |
| + | $$ | ||
| − | The family of operators | + | The family of operators $ \{ A , B _ {1} \dots B _ {m/2} \} $ |
| + | defines an elliptic boundary value problem if the function $ \xi \rightarrow r _ {jk} ( \xi ) $ | ||
| + | is non-singular on $ S( M) $. | ||
| + | Here $ r _ {jk} $ | ||
| + | are the coefficients of the polynomials | ||
| − | + | $$ | |
| + | r _ {j} ( \xi , \lambda ) = \ | ||
| + | \sum _ { k= } 0 ^ { {m } / 2 - 1 } | ||
| + | r _ {jk} ( \xi ) \lambda ^ {k} | ||
| + | $$ | ||
| − | that are the remainders after division of the polynomials | + | that are the remainders after division of the polynomials $ b _ {j} ( \xi , \lambda ) $( |
| + | in $ \lambda $) | ||
| + | by the polynomial $ a ^ {+} ( \xi , \lambda ) $( | ||
| + | in $ \lambda $), | ||
| + | where | ||
| − | + | $$ | |
| + | b _ {j} ( \xi , \lambda ) = \ | ||
| + | \sum _ {| \alpha | = m _ {j} } | ||
| + | B _ {j \alpha } ( x) ( \xi + \lambda \nu ) ^ \alpha , | ||
| + | $$ | ||
| − | and | + | and $ a ^ {+} $ |
| + | is defined from the factorization $ a = a ^ {+} a ^ {-} $, | ||
| + | where | ||
| − | + | $$ | |
| + | a ( \xi , \lambda ) = \ | ||
| + | \sum _ {| \alpha | = m } | ||
| + | A _ \alpha ( x) | ||
| + | ( \xi + \lambda \nu ) ^ \alpha , | ||
| + | $$ | ||
| − | + | $ x \in M $; | |
| + | $ \xi $, | ||
| + | $ \nu $ | ||
| + | are, respectively, a unit tangent vector and the inward normal to $ M $; | ||
| + | $ a ^ {+} $( | ||
| + | or $ a ^ {-} $) | ||
| + | is a polynomial (in $ \lambda $) | ||
| + | without zeros in the upper (respectively, lower) $ \lambda $- | ||
| + | half-plane. By the index of the above-described boundary value problem one means the index of the corresponding linear operator $ \mathfrak A $ | ||
| + | from $ C ^ \infty ( \Omega ) $ | ||
| + | into $ C ^ \infty ( \Omega ) \times C ^ \infty ( M) ^ {m/2} $ | ||
| + | taking $ u \in C ^ \infty ( \Omega ) $ | ||
| + | into the set $ \{ A u , B _ {1} u | _ {M} \dots B _ {m/2} u | _ {M} \} $. | ||
| + | It turns out that the index of the elliptic boundary value problem is the same as that of the elliptic pseudo-differential operator on $ M $ | ||
| + | whose symbol is given by the matrix $ r = ( r _ {jk} ) $. | ||
| + | In particular, the index of the Dirichlet problem $ \{ A , 1 , \partial / \partial u \dots ( \partial / \partial u ) ^ {- 1 + m / 2 } \} $ | ||
| + | is zero. There are general index formulas for boundary value problems [[#References|[16]]], , [[#References|[27]]]. | ||
==The Atiyah–Singer index formulas.== | ==The Atiyah–Singer index formulas.== | ||
| − | Let | + | Let $ C ^ \infty ( \xi ) $ |
| + | and $ C ^ \infty ( \eta ) $ | ||
| + | be the spaces of infinitely-differentiable sections of the vector bundles $ \xi $ | ||
| + | and $ \eta $ | ||
| + | over a closed $ n $- | ||
| + | dimensional differentiable manifold $ M $, | ||
| + | and let $ D $ | ||
| + | be a (pseudo-differential) elliptic operator acting from $ C ^ \infty ( \xi ) $ | ||
| + | into $ C ^ \infty ( \eta ) $. | ||
| + | The topological index $ i _ {t} ( D) $ | ||
| + | of $ D $ | ||
| + | is defined as follows. Because of the ellipticity of $ D $ | ||
| + | the symbol $ \sigma ( D) $ | ||
| + | of $ D $ | ||
| + | determines an isomorphism of the lifted vector bundles on $ S ( M) $: | ||
| − | + | $$ | |
| + | \sigma ( D) : \pi ^ {*} ( \xi ) \rightarrow \pi ^ {*} ( \eta ) , | ||
| + | $$ | ||
| − | where | + | where $ \pi : S ( M) \rightarrow M $ |
| + | is the bundle of unit spheres of the cotangent bundle $ T ^ {*} M $ | ||
| + | of $ M $. | ||
| + | Let $ B ( M) $ | ||
| + | be the bundle of unit balls in $ T ^ {*} M $; | ||
| + | this is a $ 2 n $- | ||
| + | dimensional manifold with boundary $ S ( M) $. | ||
| + | By glueing the copies $ B ^ {+} ( M) $ | ||
| + | and $ B ^ {-} ( M) $ | ||
| + | of $ B ( M) $ | ||
| + | along their common boundary, one obtains a closed $ 2 n $- | ||
| + | dimensional manifold $ \Sigma ( M) = B ^ {+} \cup _ {S ( M) } B ^ {-} $ | ||
| + | over which the vector bundle | ||
| − | + | $$ | |
| + | V ( \sigma ) = \ | ||
| + | \pi ^ {+ * } ( \xi ) \cup _ {\sigma ( D) } \pi ^ {- * } ( \eta ) | ||
| + | $$ | ||
| − | is constructed, where | + | is constructed, where $ \pi ^ \pm : B ^ \pm ( M) \rightarrow M $ |
| + | and $ \sigma ( D) $ | ||
| + | is used to identify $ \xi $ | ||
| + | and $ \eta $ | ||
| + | along $ S ( M) $. | ||
| + | This vector bundle $ V( \sigma ) $ | ||
| + | carries all the topological information required for the definition of the topological index. Namely: | ||
| − | + | $$ \tag{2 } | |
| + | i _ {t} ( D) = \ | ||
| + | \{ \mathop{\rm ch} ( V ( \sigma ) ) \cdot \pi _ \Sigma ^ {*} {\mathcal T} | ||
| + | ( M) \} [ \Sigma ( M) ] . | ||
| + | $$ | ||
| − | Here | + | Here $ \mathop{\rm ch} ( V ( \sigma ) ) $ |
| + | is the cohomological [[Chern character|Chern character]] of the bundle $ V ( \sigma ) $; | ||
| + | $ {\mathcal T} ( M) $ | ||
| + | is the cohomological [[Todd class|Todd class]] of the complexified cotangent bundle $ T ^ {*} M \otimes _ {\mathbf R} \mathbf C $; | ||
| + | $ \pi _ \Sigma : \Sigma ( M) \rightarrow M $; | ||
| + | $ \pi _ \Sigma ^ {*} {\mathcal T} ( M) = {\mathcal T} ( \Sigma ( M) ) $. | ||
| + | The right-hand side represents the value of the $ 2 n $- | ||
| + | dimensional component of the element $ \mathop{\rm ch} ( V( \sigma ) ) \cdot \pi _ \Sigma ^ {*} {\mathcal T} ( M) $ | ||
| + | on the [[Fundamental cycle|fundamental cycle]] of the manifold $ [ \Sigma ( M) ] $. | ||
| + | Thus, the mapping $ V ( \sigma ( D) ) \rightarrow i _ {t} ( D) $ | ||
| + | determines a homomorphism $ K ( \Sigma ( M) ) \rightarrow \mathbf Z $ | ||
| + | that is trivial on the image of $ K ( M) $; | ||
| + | here $ K ( X) $ | ||
| + | is the [[Grothendieck group|Grothendieck group]] generated by complex vector bundles over $ X $. | ||
The Atiyah–Singer index theorem states: | The Atiyah–Singer index theorem states: | ||
| − | + | $$ \tag{3 } | |
| + | i _ {a} ( D) = i _ {t} ( D) . | ||
| + | $$ | ||
| − | Formula (2) admits a number of modifications. The rational cohomology class | + | Formula (2) admits a number of modifications. The rational cohomology class $ \mathop{\rm ch} [ \sigma ( D) ] $, |
| + | depending on the symbol $ \sigma ( D) $, | ||
| + | is introduced as follows. With the triple $ \{ \pi ^ {*} ( \xi ) , \pi ^ {*} ( \eta ) , \sigma ( D) \} $ | ||
| + | one can associate a difference element (cf. [[Difference-element-in-K-theory|Difference element in $ K $- | ||
| + | theory]]), which can be regarded as the first [[Obstruction|obstruction]] to extending the isomorphism $ \sigma $ | ||
| + | to the whole of $ B ( M) $, | ||
| − | + | $$ | |
| + | [ \sigma ( D) ] \in K ( B ( M) / S ( M) ) = K ( T M ) , | ||
| + | $$ | ||
| − | where | + | where $ T M $ |
| + | is the tangent bundle, which (by means of the Riemannian metric on $ M $) | ||
| + | can be identified with $ T ^ {*} M $; | ||
| + | $ K ( B / S ) $ | ||
| + | is the relative Grothendieck group of vector bundles over $ B / S $, | ||
| + | and hence for the Chern character of $ [ \sigma ( D) ] $: | ||
| + | $ \mathop{\rm ch} [ \sigma ( D) ] \in H ^ {*} ( B / S ; \phi ) $. | ||
| + | The formula for the topological index of $ D $ | ||
| + | now takes the form: | ||
| − | + | $$ \tag{4 } | |
| + | i _ {t} ( D) = \ | ||
| + | ( - 1 ) ^ {n} | ||
| + | \{ \mathop{\rm ch} [ \sigma ( D) ] \cdot \pi ^ {*} {\mathcal T} ( M) \} [ T M ] , | ||
| + | $$ | ||
| − | where | + | where $ \pi : T M \rightarrow M $, |
| + | $ \pi ^ {*} {\mathcal T} ( M) = {\mathcal T} ( T M ) $. | ||
The [[Thom isomorphism|Thom isomorphism]] | The [[Thom isomorphism|Thom isomorphism]] | ||
| − | + | $$ | |
| + | \phi _ {*} : H ^ {*} ( B / S ) = H ^ {*} ( T M ) \rightarrow H ^ {*} ( M) | ||
| + | $$ | ||
then enables one to write (4) in the form | then enables one to write (4) in the form | ||
| − | + | $$ \tag{5 } | |
| + | i _ {t} ( D) = \ | ||
| + | ( - 1 ) ^ {n ( n + 1 ) / 2 } | ||
| + | \{ \phi _ {*} \mathop{\rm ch} [ \sigma ( D) ] \cdot {\mathcal T} ( M) \} [ M ] . | ||
| + | $$ | ||
(As before, on the right-hand side of (4) and (5) are the values of the corresponding elements on the fundamental cycles, as in (2).) | (As before, on the right-hand side of (4) and (5) are the values of the corresponding elements on the fundamental cycles, as in (2).) | ||
| − | The topological index is expressed in terms of | + | The topological index is expressed in terms of $ K $- |
| + | theory as follows. Let $ i : M \rightarrow E $ | ||
| + | be a differentiable imbedding of $ M $ | ||
| + | in a Euclidean space, $ W $ | ||
| + | a tubular neighbourhood of $ M $ | ||
| + | in $ E $, | ||
| + | which can be regarded as a real vector bundle over $ M $, | ||
| + | so that $ T W $ | ||
| + | is isomorphic (over $ \mathbf R $) | ||
| + | to $ \pi ^ {*} ( W \otimes _ {\mathbf R} \mathbf C ) $, | ||
| + | the complexification of $ W $ | ||
| + | lifted to $ T M $ | ||
| + | by the projection $ \pi : T M \rightarrow M $. | ||
| + | Composition of the Thom isomorphism $ \phi : K ( T M ) \rightarrow K ( T W ) $ | ||
| + | with the natural homomorphism $ K ( T W ) \rightarrow K ( T E ) $ | ||
| + | induced by the imbedding $ W \rightarrow E $ | ||
| + | induces a homomorphism $ i _ {!} : K ( T M ) \rightarrow K ( T E ) $. | ||
| + | Let $ \beta : K ( T E ) \rightarrow \mathbf Z $ | ||
| + | be the Bott periodicity isomorphism. Then the homomorphism $ \beta \circ i _ {!} : K ( T M) \rightarrow \mathbf Z $ | ||
| + | does not depend on the imbedding and | ||
| − | + | $$ | |
| + | i _ {t} ( D) = \beta \circ i _ {!} ( [ \sigma ( D) ] ) . | ||
| + | $$ | ||
==Examples.== | ==Examples.== | ||
| + | 3) Let $ M $ | ||
| + | be a closed oriented Riemannian manifold, let $ \xi ^ {k} = \wedge ^ {k} ( T ^ {*} M ) \otimes \mathbf C $ | ||
| + | be the bundle of complex exterior $ k $- | ||
| + | forms over $ M $ | ||
| + | and let | ||
| − | + | $$ | |
| − | + | d : C ^ \infty ( \xi ^ {k} ) \rightarrow C ^ \infty ( \xi ^ {k+} 1 ) ,\ \ | |
| − | + | d ^ {*} : C ^ \infty ( \xi ^ {k+} 1 ) \rightarrow C ^ \infty ( \xi ^ {k} ) | |
| + | $$ | ||
be the exterior differentiation operator and its adjoint, respectively. The operator | be the exterior differentiation operator and its adjoint, respectively. The operator | ||
| − | + | $$ | |
| + | d + d ^ {*} : C ^ \infty ( \xi ^ {e} ) \rightarrow C ^ \infty ( \xi ^ {0} ) , | ||
| + | $$ | ||
| − | where | + | where $ \xi ^ {e} = \oplus _ {p} \xi ^ {2p} $, |
| + | $ \xi ^ {0} = \oplus _ {p} \xi ^ {2p+} 1 $, | ||
| + | is elliptic and the index formula (3) holds for it; furthermore the topological index is equal to the [[Euler characteristic|Euler characteristic]] $ \chi ( M) $( | ||
| + | the Hodge–de Rham theorem). For $ \mathop{\rm dim} M = 2 $ | ||
| + | the Gauss–Bonnet theorem follows. | ||
| − | 4) Let | + | 4) Let $ \xi ^ \pm $ |
| + | be the eigen $ ( \pm ) $- | ||
| + | spaces of the involution $ I ( \alpha ) = i ^ {p ( p - 1 ) + k } \star \alpha $, | ||
| + | $ \alpha \in \xi ^ {p} $, | ||
| + | where $ \star $ | ||
| + | is the duality operator determined by the metric on $ M $, | ||
| + | $ \mathop{\rm dim} M = 2 k $. | ||
| + | The restriction of the operator $ d + d ^ {*} $ | ||
| + | to an operator from $ C ^ \infty ( \xi ^ {+} ) $ | ||
| + | into $ C ^ \infty ( \xi ^ {-} ) $, | ||
| + | called the signature operator $ \delta _ {M} $, | ||
| + | is an elliptic operator for which the index formula (3) holds; furthermore, the analytic index is equal to the [[Signature|signature]] of the manifold $ M $, | ||
| + | while the topological index is equal to the [[L-genus| $ L $- | ||
| + | genus]] (Hirzebruch's theorem). | ||
| − | 5) Let | + | 5) Let $ \eta $ |
| + | be a holomorphic vector bundle over the complex compact manifold $ M $, | ||
| + | let $ \xi ^ {0,q} $ | ||
| + | be the bundle of differential forms of type $ ( 0 , q ) $, | ||
| + | let $ \eta \otimes \xi ^ {0,q} $ | ||
| + | be the bundle of forms of type $ ( 0 , q ) $ | ||
| + | with coefficients in $ \eta $, | ||
| + | and let $ \zeta ^ {0,q} $ | ||
| + | be the $ \mathbf C $- | ||
| + | module of smooth sections of this bundle. Let $ \overline \partial \; : \xi ^ {0,q} \rightarrow \xi ^ {0,q+} 1 $ | ||
| + | be the Cauchy–Riemann–Dolbeault operator, $ \overline \partial \; {} ^ {*} $ | ||
| + | its adjoint, and let $ \xi ^ {e} = \oplus _ {p} \xi ^ {0,2p} $, | ||
| + | $ \xi ^ {0} = \oplus _ {p} \xi ^ {0,2p+} 1 $. | ||
| + | Then the operator $ \overline \partial \; + \overline \partial \; {} ^ {*} : \xi ^ {e} \rightarrow \xi ^ {0} $ | ||
| + | is an elliptic operator for which (3) holds; furthermore, the analytic index is equal to the Euler characteristic of $ M $ | ||
| + | with coefficients in the sheaf of germs of holomorphic sections of $ \eta $, | ||
| + | while the topological index is $ \{ \mathop{\rm ch} \eta \cdot {\mathcal T} ( M) \} [ M ] $, | ||
| + | where $ \mathop{\rm ch} \eta $ | ||
| + | is the Chern character of $ \eta $ | ||
| + | and $ {\mathcal T} ( M) $ | ||
| + | is the Todd class of the tangent bundle to $ M $( | ||
| + | the Riemann–Roch–Hirzebruch theorem). | ||
==Elliptic complexes.== | ==Elliptic complexes.== | ||
| − | In the more general situation which arises naturally, for example, in differential geometry, instead of a single operator | + | In the more general situation which arises naturally, for example, in differential geometry, instead of a single operator $ D $ |
| + | one considers a complex of (pseudo-differential) operators | ||
| + | |||
| + | $$ | ||
| + | A : 0 \rightarrow C ^ \infty ( \xi _ {0} ) \mathop \rightarrow \limits ^ { {D _ {0} }} C ^ \infty ( \xi _ {1} ) \mathop \rightarrow \limits ^ { {D _ {1} }} \dots \rightarrow ^ { {D _ N-} 1 } C ^ \infty ( \xi _ {N} ) \rightarrow 0 , | ||
| + | $$ | ||
| + | |||
| + | where the $ \xi _ {j} $ | ||
| + | are differentiable vector bundles over the closed manifold $ M $ | ||
| + | and $ D _ {j+} 1 D _ {j} = 0 $. | ||
| + | By the symbol of the complex $ A $ | ||
| + | one means the corresponding sequence of principal symbols | ||
| − | + | $$ | |
| + | \sigma ( A) : 0 \rightarrow \ | ||
| + | \pi ^ {*} ( \xi _ {0} ) \rightarrow ^ { {\sigma _ 0} } | ||
| + | \pi ^ {*} ( \xi _ {1} ) \rightarrow ^ { {\sigma _ 1} } | ||
| + | {} \dots \rightarrow ^ { {\sigma _ N-} 1 } | ||
| + | \pi ^ {*} ( \xi _ {N} ) \rightarrow 0 , | ||
| + | $$ | ||
| − | where the | + | where $ \pi ^ {*} ( \xi _ {j} ) $ |
| + | is the lifting of $ \xi _ {j} $ | ||
| + | to $ S ( M) $ | ||
| + | by the projection $ \pi : T ^ {*} M \rightarrow M $. | ||
| + | The complex $ A $ | ||
| + | is called elliptic if its symbol is an acyclic complex, that is, if it is exact everywhere outside the zero section. By the analytic index of the complex $ A $ | ||
| + | one means its Euler characteristic: | ||
| − | + | $$ | |
| + | i _ {a} ( A) = \chi ( A) = \ | ||
| + | \sum _ { j= } 0 ^ { N } ( - 1 ) ^ {j} | ||
| + | \mathop{\rm dim} H ^ {j} ( A) , | ||
| + | $$ | ||
| − | where | + | where $ H ^ {j} ( A) $ |
| + | is the $ j $- | ||
| + | th cohomology group of $ A $. | ||
| + | Two important examples of elliptic complexes are the de Rham complex and its complex analogue, the Dolbeault complex. The problem of computing $ \chi ( A) $ | ||
| + | in terms of the class of the complex $ \sigma ( A) $ | ||
| + | in $ K ( T M ) $ | ||
| + | can be reduced to computing the index for a single operator [[#References|[3]]]. | ||
| − | + | If a compact group $ G $ | |
| + | acts on $ A $( | ||
| + | and commutes with the action of $ D _ {j} $, | ||
| + | that is, $ A $ | ||
| + | is a $ G $- | ||
| + | complex), then $ H ^ {j} ( A) $ | ||
| + | is a $ G $- | ||
| + | module, and $ \chi ( A) $ | ||
| + | is defined as an element of the ring of characters of the group $ G $. | ||
| + | This is a function in $ C ^ \infty ( G) $. | ||
| + | Here it turns out that the index theorem can be regarded as a generalization of the [[Lefschetz theorem|Lefschetz theorem]] on fixed points, since the topological index at a point $ g \in G $ | ||
| + | can be expressed in terms of the index of the restriction of the symbol to the subset $ M ^ {g} \subset M $ | ||
| + | of fixed points of the mapping defined by $ g $. | ||
| − | + | Let $ G $ | |
| + | be a topological cyclic group, that is, there exists an element $ g $ | ||
| + | in $ G $ | ||
| + | whose powers are dense in $ G $, | ||
| + | let $ N ^ {g} $ | ||
| + | be the normal bundle to $ M ^ {g} $ | ||
| + | in $ M $ | ||
| + | and let $ [ \sigma ( S) ] \in K _ {G} ( T M ) $ | ||
| + | be the class of the symbol of $ A $. | ||
| + | Let $ i ^ {*} [ \sigma ( A)] ( g) \in K _ {G} ( T M ^ {g} ) $ | ||
| + | be its restriction and let $ \lambda _ {-} 1 ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) ( g) $ | ||
| + | be the class generated by the standard complex of exterior powers of the bundle $ \pi ^ {*} ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) $ | ||
| + | to $ M ^ {g} $( | ||
| + | here $ i : M ^ {g} \rightarrow M $, | ||
| + | $ \pi : T M ^ {g} \rightarrow M ^ {g} $). | ||
| + | Then the Lefschetz number $ L ( g , A ) $, | ||
| + | which is equal to $ \Sigma ( - 1 ) ^ {j} \mathop{\rm Tr} ( g \mid H ^ {j} ( A) ) $, | ||
| + | is given by the formula | ||
| − | + | $$ | |
| + | L ( g , A ) = \ | ||
| + | \mathop{\rm ind} \left \{ | ||
| + | \frac{i ^ {*} [ \sigma ( A) ] ( g) }{\lambda _ {-} 1 ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) ( g) } | ||
| − | + | \right \} = \ | |
| + | \mathop{\rm ind} _ {G} A ( g) , | ||
| + | $$ | ||
| − | + | where $ \mathop{\rm ind} : K ( T M ^ {g} ) \otimes \mathbf C \rightarrow \mathbf C $ | |
| + | is the natural extension of the topological index $ K ( T M ^ {g} ) \rightarrow \mathbf Z $. | ||
| + | The cohomological version of this formula is given by: | ||
| − | + | $$ \tag{6 } | |
| + | \mathop{\rm ind} _ {G} A ( g) = \ | ||
| + | \left \{ | ||
| − | + | \frac{ \mathop{\rm ch} i ^ {*} [ \sigma ( A) ] ( g) }{ \mathop{\rm ch} \lambda _ {-} 1 ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) ( g) } | |
| + | \ | ||
| + | \cdot \pi ^ {*} {\mathcal T} ( M ^ {g} ) \right \} | ||
| + | [ M ] . | ||
| + | $$ | ||
| − | Without the compactness condition on | + | Without the compactness condition on $ G $, |
| + | but under the hypothesis that $ M ^ {g} $ | ||
| + | is a zero-dimensional submanifold and that the action of $ G $ | ||
| + | is non-degenerate (that is, the graph of $ g $ | ||
| + | is transversal to the diagonal in $ M \times M $), | ||
| + | there is an analogous formula, which can be expressed as follows. If $ P \in M ^ {g} $, | ||
| + | then $ d g ( P) $ | ||
| + | leaves $ T M \mid _ {P} $ | ||
| + | fixed while $ g $ | ||
| + | induces a linear mapping $ l _ {j} ( g , P ) $ | ||
| + | on the fibres $ \xi _ {j} \mid _ {P} $, | ||
| + | and | ||
| − | + | $$ | |
| + | \mathop{\rm ind} _ {G} A ( g) = \ | ||
| + | \sum _ {P \in M ^ {g} } | ||
| + | \sum _ { j } | ||
| + | ( - 1 ) ^ {j} | ||
| − | Finally, it is possible to weaken the condition of ellipticity of the | + | \frac{ \mathop{\rm Tr} l _ {j} ( g , P ) }{ \mathop{\rm det} ( 1 - d g ( P) ) } |
| + | . | ||
| + | $$ | ||
| + | |||
| + | Finally, it is possible to weaken the condition of ellipticity of the $ G $- | ||
| + | complex $ A $ | ||
| + | by considering so-called transversally-elliptic complexes; in this case, the index turns out to be a generalized function on the group $ G $( | ||
| + | see [[#References|[8]]]). In particular, if $ G $ | ||
| + | is finite, then transversal ellipticity is to equivalent to ellipticity, so that the previous formulas are applicable. If $ M = G / H $ | ||
| + | is a homogeneous space, then all the complexes of operators are transversally elliptic and in this case the index formula is in essence the same as the Frobenius reciprocity formula for the induced representations of the group $ G $. | ||
==Non-Fredholm operators.== | ==Non-Fredholm operators.== | ||
| Line 140: | Line 512: | ||
==Examples.== | ==Examples.== | ||
| + | 6) Let $ D $ | ||
| + | be a uniformly-elliptic operator on $ \mathbf R ^ {n} $ | ||
| + | with almost-periodic coefficients. The analytic index $ i _ {a} ( D) $ | ||
| + | is introduced by means of the relative dimension in the $ \textrm{ II } _ \infty $- | ||
| + | factor (see [[Von Neumann algebra|von Neumann algebra]]) and is a real number (see [[#References|[11]]]). There is a formula analogous to (1), but instead of the integral over $ \mathbf R ^ {n} $ | ||
| + | the average value of the almost-periodic function is used. | ||
| − | + | 7) Suppose that a discrete group $ \Gamma $ | |
| + | acts freely on a manifold $ M $ | ||
| + | and that the quotient space $ \widetilde{M} = M / \Gamma $ | ||
| + | is compact; let $ \xi $, | ||
| + | $ \eta $ | ||
| + | be vector bundles over $ M $ | ||
| + | and let $ \Gamma $ | ||
| + | act on them in accordance with its action on $ M $. | ||
| + | The analytic index of an elliptic operator $ D : C ^ \infty ( \xi ) \rightarrow C ^ \infty ( \eta ) $ | ||
| + | on $ M $ | ||
| + | commuting with the action of $ \Gamma $ | ||
| + | is defined by the formula | ||
| − | 7 | + | $$ \tag{7 } |
| + | i _ {a} ( D) = \ | ||
| + | \mathop{\rm Tr} _ \Gamma P _ {1} - \mathop{\rm Tr} _ \Gamma P _ {2} , | ||
| + | $$ | ||
| − | + | where $ P _ {1} $, | |
| + | $ P _ {2} $ | ||
| + | are the orthogonal projections on $ \mathop{\rm Ker} D $ | ||
| + | and $ \mathop{\rm Ker} D ^ {*} $ | ||
| + | in $ L _ {2} ( M , d \mu ) $, | ||
| + | $ d \mu $ | ||
| + | is any $ \Gamma $- | ||
| + | invariant smooth density on $ M $ | ||
| + | and $ \mathop{\rm Tr} _ \Gamma P $ | ||
| + | is defined, for any operator $ P $ | ||
| + | commuting with $ \Gamma $ | ||
| + | and having smooth kernel $ P ( x , y ) $, | ||
| + | by the formula | ||
| − | + | $$ | |
| + | \mathop{\rm Tr} _ \Gamma P = \ | ||
| + | \int\limits _ {M _ {0} } | ||
| + | \mathop{\rm tr} P ( x , x ) d \mu | ||
| + | $$ | ||
| − | + | (here $ M _ {0} $ | |
| + | is any fundamental domain of the group $ \Gamma $ | ||
| + | on $ M $ | ||
| + | and $ \mathop{\rm tr} $ | ||
| + | is the trace of the matrix). It turns out that $ i _ {a} ( D) = i _ {a} ( \widetilde{D} ) $, | ||
| + | where $ \widetilde{D} $ | ||
| + | is the operator on $ \widetilde{M} $ | ||
| + | whose symbol $ \widetilde \sigma ( D) $ | ||
| + | induces $ \sigma ( D) $ | ||
| + | under the lifting to $ M $ | ||
| + | by the canonical projection $ \pi : M \rightarrow \widetilde{M} $[[#References|[12]]]. Thus, the index formula for the operator $ D $ | ||
| + | can be obtained from the index formula for the operator $ \widetilde{D} $ | ||
| + | on the compact manifold $ \widetilde{M} $. | ||
| + | This result enables one to reveal the non-triviality of spaces in which representations of discrete series are realized [[#References|[13]]]. | ||
| − | + | A formula of the same type can be obtained for invariant elliptic operators on homogeneous spaces of Lie groups, even without $ \Gamma $ | |
| + | being discrete, with a natural generalization of the analytic index [[#References|[20]]]. | ||
| − | + | Another generalization of this situation can be obtained if one considers invariant operators on a manifold $ M $ | |
| + | with an action of a locally compact group $ G $ | ||
| + | such that $ M / G $ | ||
| + | is compact [[#References|[24]]]. | ||
| − | + | 8) If the coefficients of a uniformly-elliptic operator $ D $ | |
| + | on $ \mathbf R ^ {n} $ | ||
| + | form a homogeneous measurable random field, then it is possible to introduce the analytic index $ i _ {a} ( D) $, | ||
| + | which is a random variable (in the ergodic case, a real number) defined by formula (7) with $ \mathop{\rm Tr} _ \Gamma P $ | ||
| + | replaced by $ \mathop{\rm Tr} P $. | ||
| + | Here $ \mathop{\rm Tr} P $ | ||
| + | is constructed from the kernel $ P ( x , y ) $ | ||
| + | of the operator $ P $ | ||
| + | by averaging over $ x $: | ||
| + | $ \mathop{\rm Tr} P = M _ {x} \{ \mathop{\rm tr} P ( x , x ) \} $. | ||
| + | This example is a generalization of Example 6) and an analogous index formula holds for it . | ||
| − | + | 9) Let $ M $ | |
| + | be a compact manifold with a foliation $ {\mathcal F} $ | ||
| + | and $ D $ | ||
| + | a longitudinal elliptic differential operator on $ M $, | ||
| + | i.e. a differential operator containing only differentiations along the leaves and elliptic on every leaf. Suppose that there is a transverse measure on $ {\mathcal F} $. | ||
| + | Then a real-valued analytic index of $ D $ | ||
| + | can be defined and a formula of Atiyah–Singer type can be proved. Considering measured foliations, in this context one comes to a formula which generalizes that of Example 8), [[#References|[18]]], [[#References|[19]]]. | ||
| − | + | ==Index formulas with values in $ K $-groups.== | |
| − | + | 10) If a family of elliptic operators is given, parametrized by the points $ y $ | |
| + | of a compact space $ Y $, | ||
| + | then its analytic index $ i _ {a} ( D) \in K ( Y) $ | ||
| + | has been defined (see [[#References|[15]]]). The topological index $ i _ {t} ( D) $ | ||
| + | is constructed by analogy with formula (6) (all the constructions are carried out "fibrewise" over $ Y $) | ||
| + | and the index theorem holds. | ||
| + | 11) A more general theorem is obtained if one considers elliptic operators over a compact manifold acting in sections of vector bundles with fibres which are finitely-generated projective modules over a fixed $ C ^ {*} $- | ||
| + | algebra $ {\mathcal A} $. | ||
| + | The analytic index here takes values in the group $ K ^ {0} ( {\mathcal A} ) $. | ||
| + | If one takes $ {\mathcal A} = C ( Y) $ | ||
| + | with a compact $ Y $, | ||
| + | then one obtains the formula of Example 10). Also the equivalent situation (with a compact Lie group $ G $) | ||
| + | can be considered in this context [[#References|[26]]], [[#References|[29]]]. | ||
| − | + | The case when $ A $ | |
| + | is a $ \textrm{ II } _ {1} $- | ||
| + | factor is of particular interest [[#References|[28]]], implying the formula of Example 7). | ||
| − | + | 12) There is a number of generalizations of the Atiyah–Singer formulas with the analytic index taking values in homology $ K $- | |
| + | groups or bivariant Kasparov $ K $- | ||
| + | groups. Taking the Chern character and applying some kind of intersection index usually allows one to pass to the usual number-valued index formulas [[#References|[23]]], [[#References|[25]]]. Also, the longitudinal index theorem of Example 9) can be generalized in this manner [[#References|[21]]]. | ||
| − | + | 13) Consider two generalized Dirac operators $ D _ {0} $, | |
| + | $ D _ {1} $ | ||
| + | which coincide near infinity (in particular, they are defined on Riemannian manifolds $ M _ {0} $, | ||
| + | $ M _ {1} $ | ||
| + | which coincide near infinity, i.e. $ M _ {0} \setminus K _ {0} $ | ||
| + | and $ M _ {1} \setminus K _ {1} $ | ||
| + | are isometric for some compact subsets $ K _ {j} \subset M _ {j} $, | ||
| + | $ j = 1 , 2 $). | ||
| + | Let $ D _ {0} $, | ||
| + | $ D _ {1} $ | ||
| + | be positive near infinity and let there be the natural splittings | ||
| − | + | $$ | |
| + | D _ {j} = \left ( | ||
| − | + | \begin{array}{cc} | |
| + | 0 &{D _ {j} ^ {-} } \\ | ||
| + | {D _ {j} ^ {+} } & 0 \\ | ||
| + | \end{array} | ||
| + | \right ) ,\ \ | ||
| + | j = 1 , 2 . | ||
| + | $$ | ||
| − | + | Then $ \mathop{\rm ind} D _ {1} ^ {+} - \mathop{\rm ind} D _ {0} ^ {+} $ | |
| − | + | can be expressed by a formula of Atiyah–Singer type having important geometrical applications [[#References|[22]]]. | |
| − | |||
==New analytic tools.== | ==New analytic tools.== | ||
The Atiyah–Bott formula | The Atiyah–Bott formula | ||
| − | + | $$ | |
| + | \mathop{\rm ind} D = \mathop{\rm Tr} \mathop{\rm exp} | ||
| + | ( - t D ^ {*} D ) - \mathop{\rm Tr} \mathop{\rm exp} | ||
| + | ( - t D D ^ {*} ) | ||
| + | $$ | ||
| − | provides a local expression of the index if one uses the asymptotic expansion of the traces on the right-hand side as | + | provides a local expression of the index if one uses the asymptotic expansion of the traces on the right-hand side as $ t \downarrow 0 $. |
| + | But this expression contains lower-order terms of the symbol of $ D $, | ||
| + | so it seems difficult to see how the corresponding integrals cancel. It occurred that cancellation is obtained by using some symmetry and supersymmetry arguments. Also a probabilistic approach is effective to work with the traces of heat kernels. Families of elliptic operators can be considered in this way too [[#References|[30]]]–[[#References|[42]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Gel'fand, "On elliptic differential equations" ''Russian Math. Surveys'' , '''15''' : 3 (1960) pp. 113–123 ''Uspekhi Mat. Nauk'' , '''15''' : 3 (1960) pp. 121–132</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators on compact manifolds" ''Bull. Amer. Math. Soc.'' , '''69''' (1963) pp. 422–433 {{MR|0157392}} {{ZBL|0118.31203}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" ''Ann. of Math.'' , '''87''' (1968) pp. 484–530 {{MR|0236950}} {{MR|0232402}} {{ZBL|0164.24001}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.F. Atiyah, G.B. Segal, "The index of elliptic operators II" ''Ann. of Math.'' , '''87''' (1968) pp. 531–545 {{MR|0236953}} {{MR|0236951}} {{ZBL|0164.24201}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators III" ''Ann. of Math.'' , '''87''' (1968) pp. 546–604 {{MR|0236952}} {{ZBL|0164.24301}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators IV" ''Ann. of Math.'' , '''93''' (1971) pp. 119–138 {{MR|0279833}} {{ZBL|0212.28603}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.V. Fedosov, "Analytic formulas for the index of elliptic operators" ''Trans. Moscow Math. Soc.'' , '''30''' (1974) pp. 279–330 ''Trudy Moskov. Mat. Obshch.'' , '''30''' (1974) pp. 159–241 {{MR|0420731}} {{ZBL|0349.58006}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> M.F. Atiyah, "Elliptic operators and compact groups" , ''Lect. notes in math.'' , '''401''' , Springer (1974) {{MR|0482866}} {{ZBL|0297.58009}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) {{MR|0198494}} {{ZBL|0137.17002}} </TD></TR><TR><TD valign="top">[10a]</TD> <TD valign="top"> M.F. Atiyah, R. Bott, V.K. Patodi, "On the heat equation and the index theorem" ''Invent. Math.'' , '''19''' (1973) pp. 279–330 {{MR|0650828}} {{ZBL|0364.58016}} {{ZBL|0257.58008}} </TD></TR><TR><TD valign="top">[10b]</TD> <TD valign="top"> M.F. Atiyah, R. Bott, V.K. Patodi, "Errata to "On the heat equation and the index theorem" " ''Invent. Math.'' , '''28''' (1975) pp. 277–280 {{MR|0650829}} {{ZBL|0301.58018}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> L. Coburn, R. Moyer, I.M. Singer, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650378.png" />-algebras of almost-periodic pseudo-differential operators" ''Acta Math.'' , '''130''' : 3–4 (1973) pp. 279–307 {{MR|0415407}} {{ZBL|0263.47042}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> M.F. Atiyah, "Elliptic operators, discrete groups and von Neumann algebras" ''Astérisque'' , '''32–33''' (1976) pp. 43–72 {{MR|0420729}} {{ZBL|0323.58015}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> M.F. Atiyah, W. Schmid, "A geometric construction of the discrete series for semisimple Lie groups" ''Invent. Math.'' , '''42''' (1977) pp. 1–62 {{MR|0463358}} {{ZBL|0373.22001}} </TD></TR><TR><TD valign="top">[14a]</TD> <TD valign="top"> B.V. Fedosov, M.A. Shubin, "The index of random elliptic operators I" ''Math. USSR Sb.'' , '''34''' (1978) pp. 671–699 ''Mat. Sb.'' , '''106''' : 1 pp. 108–140 {{MR|0501190}} {{ZBL|0448.47033}} </TD></TR><TR><TD valign="top">[14b]</TD> <TD valign="top"> B.V. Fedosov, M.A. Shubin, "The index of random elliptic operators II" ''Math. USSR Sb.'' , '''35''' (1979) pp. 131–156 ''Mat. Sb.'' , '''106''' : 3 pp. 455–483 {{MR|0501191}} {{ZBL|0422.58025}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650379.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> L. Boutet de Monvel, "Boundary problems for pseudodifferential operators" ''Acta Math.'' , '''126''' : 1–2 (1971) pp. 11–51</TD></TR><TR><TD valign="top">[17a]</TD> <TD valign="top"> B.V. Fedosov, "The analytic formula for the index of an elliptic boundary value problem" ''Mat. USSR Sb.'' , '''22''' (1974) pp. 61–90 ''Mat. Sb.'' , '''93''' : 1 (1974) pp. 62–89 {{MR|}} {{ZBL|0385.58009}} {{ZBL|0323.58016}} {{ZBL|0337.58007}} </TD></TR><TR><TD valign="top">[17b]</TD> <TD valign="top"> B.V. Fedosov, "An analytic formula for the index of an elliptic boundary value problem II" ''Mat. USSR Sb.'' , '''24''' (1974) pp. 511–535 ''Mat. Sb.'' , '''95''' : 4 (1974) pp. 525–550 {{MR|0383464}} {{ZBL|0323.58016}} </TD></TR><TR><TD valign="top">[17c]</TD> <TD valign="top"> B.V. Fedosov, "An analytic formula for the index of an elliptic boundary value problem III" ''Mat. USSR Sb.'' , '''30''' (1976) pp. 341–359 ''Mat. Sb.'' , '''101''' : 3 (1976) pp. 380–401 {{MR|448451}} {{ZBL|0385.58009}} </TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> A. Connes, "Sur la théorie non commutative de l'intégration" , ''Algèbres d'opérateurs'' , ''Lect. notes in math.'' , '''725''' , Springer (1979) pp. 19–143 {{MR|0548112}} {{ZBL|0412.46053}} </TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> A. Connes, "A survey of foliations and operator algebras" , ''Operator algebras and applications'' , ''Proc. Symp. Pure Math.'' , '''38''' : 1 , Amer. Math. Soc. (1982) pp. 521–628 {{MR|0679730}} {{ZBL|0531.57023}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> A. Connes, H. Moscovici, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650380.png" />-index theorem for homogeneous spaces of Lie groups" ''Ann. of Math.'' , '''115''' (1982) pp. 291–330 {{MR|647808}} {{ZBL|}} </TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> A. Connes, G. Skandalis, "The longitudinal index theorem for foliations" ''Publ. Res. Inst. Math. Sci. Kyoto Univ.'' , '''20''' (1984) pp. 1139–1183 {{MR|0775126}} {{ZBL|0575.58030}} </TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> M. Gromov, H.B. Lawson, "Positive scalar curvature and the Dirac operator on complete Riemannian manifolds" ''Publ. Math. IHES'' , '''58''' (1983) pp. 83–196 {{MR|0720933}} {{ZBL|0538.53047}} </TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> G.G. Kasparov, "Topological invariants of elliptic operators I. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650381.png" />-homology" ''Math. USSR Izv.'' , '''9''' (1975) pp. 751–792 ''Izv. Akad. Nauk SSSR, Ser. Mat.'' , '''39''' (1975) pp. 796–838 {{MR|488027}} {{ZBL|}} </TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> G.G. Kasparov, "An index of invariant elliptic operators, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650382.png" />-theory, and representations of Lie groups" ''Soviet Math. Dokl.'' , '''27''' (1983) pp. 105–109 ''Dokl. Akad. Nauk SSSR'' , '''268''' (1983) pp. 533–537 {{MR|691088}} {{ZBL|}} </TD></TR><TR><TD valign="top">[25]</TD> <TD valign="top"> G.G. Kasparov, "Operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650383.png" />-theory and its applications: elliptic operators, group representation, higher signatures, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650384.png" />-extensions" , ''Proc. Internat. Congress Mathematicians (Warszawa, 1983)'' , PWN & Elsevier (1984) pp. 987–1000 {{MR|804752}} {{ZBL|}} </TD></TR><TR><TD valign="top">[26]</TD> <TD valign="top"> A.S. [A.S. Mishchenko] Miščenko, A.T. Fomenko, "The index of elliptic operators over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650385.png" />-algebras" ''Math. USSR Izv.'' , '''15''' (1980) pp. 87–112 ''Izv. Akad. Nauk SSSR, Ser. Mat.'' , '''43''' (1979) pp. 831–851</TD></TR><TR><TD valign="top">[27]</TD> <TD valign="top"> S. Rempel, B.-W. Schulze, "Index theory of elliptic boundary problems" , Akademie Verlag (1982) {{MR|0690065}} {{ZBL|0504.35002}} </TD></TR><TR><TD valign="top">[28]</TD> <TD valign="top"> I.M. Singer, "Some remarks on operator theory and index theory" , ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650386.png" />-theory and operator algebras'' , ''Lect. notes in math.'' , '''757''' , Springer (1977) pp. 128–138 {{MR|0467848}} {{ZBL|0444.47040}} </TD></TR><TR><TD valign="top">[29]</TD> <TD valign="top"> E.V. Troitskii, "The equivariant index of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050650/i050650387.png" />-elliptic operators" ''Math. USSR Izv.'' , '''29''' (1987) pp. 207–224 ''Izv. Akad. Nauk SSSR, Ser. Mat.'' , '''50''' (1986) pp. 849–965</TD></TR><TR><TD valign="top">[30]</TD> <TD valign="top"> L. Alvarez-Gaumé, "Supersymmetry and the Atiyah–Singer index theorem" ''Commun. Math. Phys.'' , '''90''' (1983) pp. 161–173 {{MR|}} {{ZBL|0528.58034}} </TD></TR><TR><TD valign="top">[31]</TD> <TD valign="top"> D. Quillen, "Superconnections and the Chern character" ''Topology'' , '''24''' (1985) pp. 89–95 {{MR|0790678}} {{ZBL|0569.58030}} </TD></TR><TR><TD valign="top">[32]</TD> <TD valign="top"> N. Berline, M. Vergne, "A computation of the equivariant index of the Dirac operator" ''Bull. Soc. Math. France'' , '''113''' (1985) pp. 305–345 {{MR|0834043}} {{ZBL|0592.58044}} </TD></TR><TR><TD valign="top">[33]</TD> <TD valign="top"> N. Berline, M. Vergne, "A proof of Bismut local index theorem for a family of Dirac operators" ''Topology'' , '''26''' (1987) pp. 435–464 {{MR|0919729}} {{ZBL|0636.58030}} </TD></TR><TR><TD valign="top">[34]</TD> <TD valign="top"> J.-M. Bismut, "The Atiyah–Singer theorem: A probabilistic approach I. The index theorem" ''J. Funct. Anal.'' , '''57''' (1984) pp. 56–98 {{MR|0744920}} {{MR|0756173}} {{ZBL|}} </TD></TR><TR><TD valign="top">[35]</TD> <TD valign="top"> J.-M. Bismut, "Localization formulas, superconnections, and the index theorem for families" ''Commun. Math. Phys.'' , '''103''' (1986) pp. 127–166 {{MR|0826861}} {{ZBL|0602.58042}} </TD></TR><TR><TD valign="top">[36]</TD> <TD valign="top"> J.-M. Bismut, "The Atiyah–Singer index theorem for families of Dirac operators: two heat equation proofs" ''Invent. Math.'' , '''83''' (1986) pp. 91–151 {{MR|0813584}} {{ZBL|0592.58047}} </TD></TR><TR><TD valign="top">[37]</TD> <TD valign="top"> H. Donnelly, "Local index theorem for families" ''Michigan Math. J.'' , '''35''' (1988) pp. 11–20 {{MR|0931936}} {{ZBL|0657.58039}} </TD></TR><TR><TD valign="top">[38]</TD> <TD valign="top"> E. Getzler, "Pseudodifferential operators on supermanifolds and the Atiyah–Singer index theorem" ''Commun. Math. Phys.'' , '''92''' (1983) pp. 163–178 {{MR|0728863}} {{ZBL|0543.58026}} </TD></TR><TR><TD valign="top">[39]</TD> <TD valign="top"> E. Getzler, "A short proof of the local Atiyah–Singer index theorem" ''Topology'' , '''25''' (1988) pp. 111–117 {{MR|0836727}} {{ZBL|0607.58040}} </TD></TR><TR><TD valign="top">[40]</TD> <TD valign="top"> P. Gilkey, "Invariance theory, the heat equation and the Atiyah–Singer theorem" , Publish or Perish (1984) {{MR|783634}} {{ZBL|0565.58035}} </TD></TR><TR><TD valign="top">[41]</TD> <TD valign="top"> R. Léandre, "Sur le théorème d'Atiyah–Singer" ''Probab. Theory Related Fields'' , '''80''' (1988) pp. 119–137 {{MR|970474}} {{ZBL|}} </TD></TR><TR><TD valign="top">[42]</TD> <TD valign="top"> R. Léandre, "Sur le théorème de l'indice des familles" , ''Sem. Probab. Strasbourg XII'' , ''Lect. notes in math.'' , '''1321''' , Springer (1988) pp. 348–413 {{MR|0960536}} {{ZBL|}} </TD></TR></table> |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 198: | Line 675: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.L. Cycon, R.G. Froese, W. Kirsch, B. Simon, "Schrödinger operators" , Springer (1987) {{MR|0883643}} {{ZBL|0619.47005}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''III. Pseudo-differential operators''' , Springer (1985) {{MR|1540773}} {{MR|0781537}} {{MR|0781536}} {{ZBL|0612.35001}} {{ZBL|0601.35001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Kaku, "Introduction to superstrings" , Springer (1988) {{MR|0954610}} {{ZBL|0655.58001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> D. Friedan, P. Windey, "Supersymmetric derivation of the Atiyah–Singer index theorem and the chiral anomaly" ''Nucl. Phys.'' , '''B253''' (1984) pp. 395–416 {{MR|888706}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E. Witten, "Supersymmetry and Morse theory" ''J. Diff. Geom.'' , '''17''' (1982) pp. 661–692 {{MR|0683171}} {{ZBL|0499.53056}} </TD></TR></table> |
Latest revision as of 22:12, 5 June 2020
Relations between analytic and topological invariants of operators of a certain class. More precisely, index formulas establish a relation between the analytic index of a linear operator
$$ D : L _ {0} \rightarrow L _ {1} $$
( $ L _ {0} , L _ {1} $ are topological vector spaces), defined by the formula
$$ i _ {a} ( D) = \ \mathop{\rm dim} \mathop{\rm Ker} D - \mathop{\rm dim} \mathop{\rm Coker} D \in \mathbf Z $$
and measuring in this way the "difference" between the defective subspaces of $ D $( namely, the kernel $ \mathop{\rm Ker} D = D ^ {-} 1 ( 0) $ and its cokernel $ \mathop{\rm Coker} D = L _ {1} / D ( L _ {0} ) $), and a topological index, namely some topological characteristic of the operator $ D $ and the spaces $ L _ {0} $, $ L _ {1} $. For a general elliptic differential operator on a closed manifold, the problem of finding index formulas was posed towards the end of the 1950's [1] and solved in 1963 (see [2]), although special forms of index formulas were known even earlier, for example, the Gauss–Bonnet theorem and its multi-dimensional variants. Subsequently a number of generalizations of index formulas were obtained for objects of a more complex nature; in these cases, instead of the index, which is an integer, arbitrary complex numbers and more general objects (e.g. functions) may feature.
Elementary index formulas.
1) Let $ M $ be the differentiable boundary of a bounded region $ \Omega \subset \mathbf R ^ {n+} 1 $ and let $ A $ be an elliptic pseudo-differential operator mapping the space $ C ^ \infty ( M , \mathbf C ^ {p} ) $ of differentiable complex-valued vector functions on $ M $ with values in $ \mathbf C ^ {p} $ into itself. Let $ B( M) $ be the manifold of tangent vectors to $ M $ of length $ \leq 1 $, oriented by means of the $ 2 n $- form
$$ ( d x ^ {1} \wedge d \xi _ {1} ) \wedge \dots \wedge ( d x ^ {n} \wedge d \xi _ {n} ) , $$
where $ x ^ {1} \dots x ^ {n} $ are local coordinates on $ M $, $ \xi _ {1} \dots \xi _ {n} $ are the corresponding coordinates in the tangent space, and let $ S ( M) $ be the oriented boundary of $ B ( M) $ formed by the unit tangent vectors. Since $ A $ is elliptic, its symbol $ a $ is a non-singular $ ( p \times p ) $- matrix function on $ S ( M) $. It turns out that the following Dynin–Fedosov formula holds for the index of $ A $[7]:
$$ \tag{1 } \mathop{\rm ind} A = \ \frac{( - 1 ) ^ {n-} 1 ( n - 1 ) ! }{( 2 \pi i ) ^ {n} ( 2 n - 1 ) ! } \int\limits _ {S ( M) } \mathop{\rm Tr} ( a ^ {-} 1 d a ) ^ {\wedge ^ {2n-} 1 } , $$
where $ ( a ^ {-} 1 d a ) ^ {\wedge ^ {2n-} 1 } $ is the exterior power of the matrix exterior form $ a ^ {-} 1 d a $ and $ \mathop{\rm Tr} $ denotes the trace of the $ ( p \times p ) $- matrix form. In particular, if $ p < n $ or if $ A $ is a differential operator on an odd-dimensional manifold, then $ \mathop{\rm ind} A = 0 $( this is not true, in general, for a pseudo-differential operator).
2) Let $ A $ be an elliptic differential operator of the form
$$ A = \sum _ {| \alpha | \leq m } A _ \alpha ( x) \left ( \frac{1}{i} \frac \partial {\partial x } \right ) ^ \alpha $$
(where $ \alpha $ is a multi-index) in the space $ C ^ \infty ( \Omega ) $, and let $ B _ {1} \dots B _ {m/2} $ be boundary differential operators from $ C ^ \infty ( \Omega ) $ into $ C ^ \infty ( M) $ of the form
$$ B _ {j} = \sum _ {| \alpha | \leq m _ {j} } B _ {j \alpha } ( x) \left ( \frac{1}{i} \frac \partial {\partial x } \right ) ^ \alpha . $$
The family of operators $ \{ A , B _ {1} \dots B _ {m/2} \} $ defines an elliptic boundary value problem if the function $ \xi \rightarrow r _ {jk} ( \xi ) $ is non-singular on $ S( M) $. Here $ r _ {jk} $ are the coefficients of the polynomials
$$ r _ {j} ( \xi , \lambda ) = \ \sum _ { k= } 0 ^ { {m } / 2 - 1 } r _ {jk} ( \xi ) \lambda ^ {k} $$
that are the remainders after division of the polynomials $ b _ {j} ( \xi , \lambda ) $( in $ \lambda $) by the polynomial $ a ^ {+} ( \xi , \lambda ) $( in $ \lambda $), where
$$ b _ {j} ( \xi , \lambda ) = \ \sum _ {| \alpha | = m _ {j} } B _ {j \alpha } ( x) ( \xi + \lambda \nu ) ^ \alpha , $$
and $ a ^ {+} $ is defined from the factorization $ a = a ^ {+} a ^ {-} $, where
$$ a ( \xi , \lambda ) = \ \sum _ {| \alpha | = m } A _ \alpha ( x) ( \xi + \lambda \nu ) ^ \alpha , $$
$ x \in M $; $ \xi $, $ \nu $ are, respectively, a unit tangent vector and the inward normal to $ M $; $ a ^ {+} $( or $ a ^ {-} $) is a polynomial (in $ \lambda $) without zeros in the upper (respectively, lower) $ \lambda $- half-plane. By the index of the above-described boundary value problem one means the index of the corresponding linear operator $ \mathfrak A $ from $ C ^ \infty ( \Omega ) $ into $ C ^ \infty ( \Omega ) \times C ^ \infty ( M) ^ {m/2} $ taking $ u \in C ^ \infty ( \Omega ) $ into the set $ \{ A u , B _ {1} u | _ {M} \dots B _ {m/2} u | _ {M} \} $. It turns out that the index of the elliptic boundary value problem is the same as that of the elliptic pseudo-differential operator on $ M $ whose symbol is given by the matrix $ r = ( r _ {jk} ) $. In particular, the index of the Dirichlet problem $ \{ A , 1 , \partial / \partial u \dots ( \partial / \partial u ) ^ {- 1 + m / 2 } \} $ is zero. There are general index formulas for boundary value problems [16], , [27].
The Atiyah–Singer index formulas.
Let $ C ^ \infty ( \xi ) $ and $ C ^ \infty ( \eta ) $ be the spaces of infinitely-differentiable sections of the vector bundles $ \xi $ and $ \eta $ over a closed $ n $- dimensional differentiable manifold $ M $, and let $ D $ be a (pseudo-differential) elliptic operator acting from $ C ^ \infty ( \xi ) $ into $ C ^ \infty ( \eta ) $. The topological index $ i _ {t} ( D) $ of $ D $ is defined as follows. Because of the ellipticity of $ D $ the symbol $ \sigma ( D) $ of $ D $ determines an isomorphism of the lifted vector bundles on $ S ( M) $:
$$ \sigma ( D) : \pi ^ {*} ( \xi ) \rightarrow \pi ^ {*} ( \eta ) , $$
where $ \pi : S ( M) \rightarrow M $ is the bundle of unit spheres of the cotangent bundle $ T ^ {*} M $ of $ M $. Let $ B ( M) $ be the bundle of unit balls in $ T ^ {*} M $; this is a $ 2 n $- dimensional manifold with boundary $ S ( M) $. By glueing the copies $ B ^ {+} ( M) $ and $ B ^ {-} ( M) $ of $ B ( M) $ along their common boundary, one obtains a closed $ 2 n $- dimensional manifold $ \Sigma ( M) = B ^ {+} \cup _ {S ( M) } B ^ {-} $ over which the vector bundle
$$ V ( \sigma ) = \ \pi ^ {+ * } ( \xi ) \cup _ {\sigma ( D) } \pi ^ {- * } ( \eta ) $$
is constructed, where $ \pi ^ \pm : B ^ \pm ( M) \rightarrow M $ and $ \sigma ( D) $ is used to identify $ \xi $ and $ \eta $ along $ S ( M) $. This vector bundle $ V( \sigma ) $ carries all the topological information required for the definition of the topological index. Namely:
$$ \tag{2 } i _ {t} ( D) = \ \{ \mathop{\rm ch} ( V ( \sigma ) ) \cdot \pi _ \Sigma ^ {*} {\mathcal T} ( M) \} [ \Sigma ( M) ] . $$
Here $ \mathop{\rm ch} ( V ( \sigma ) ) $ is the cohomological Chern character of the bundle $ V ( \sigma ) $; $ {\mathcal T} ( M) $ is the cohomological Todd class of the complexified cotangent bundle $ T ^ {*} M \otimes _ {\mathbf R} \mathbf C $; $ \pi _ \Sigma : \Sigma ( M) \rightarrow M $; $ \pi _ \Sigma ^ {*} {\mathcal T} ( M) = {\mathcal T} ( \Sigma ( M) ) $. The right-hand side represents the value of the $ 2 n $- dimensional component of the element $ \mathop{\rm ch} ( V( \sigma ) ) \cdot \pi _ \Sigma ^ {*} {\mathcal T} ( M) $ on the fundamental cycle of the manifold $ [ \Sigma ( M) ] $. Thus, the mapping $ V ( \sigma ( D) ) \rightarrow i _ {t} ( D) $ determines a homomorphism $ K ( \Sigma ( M) ) \rightarrow \mathbf Z $ that is trivial on the image of $ K ( M) $; here $ K ( X) $ is the Grothendieck group generated by complex vector bundles over $ X $.
The Atiyah–Singer index theorem states:
$$ \tag{3 } i _ {a} ( D) = i _ {t} ( D) . $$
Formula (2) admits a number of modifications. The rational cohomology class $ \mathop{\rm ch} [ \sigma ( D) ] $, depending on the symbol $ \sigma ( D) $, is introduced as follows. With the triple $ \{ \pi ^ {*} ( \xi ) , \pi ^ {*} ( \eta ) , \sigma ( D) \} $ one can associate a difference element (cf. Difference element in $ K $- theory), which can be regarded as the first obstruction to extending the isomorphism $ \sigma $ to the whole of $ B ( M) $,
$$ [ \sigma ( D) ] \in K ( B ( M) / S ( M) ) = K ( T M ) , $$
where $ T M $ is the tangent bundle, which (by means of the Riemannian metric on $ M $) can be identified with $ T ^ {*} M $; $ K ( B / S ) $ is the relative Grothendieck group of vector bundles over $ B / S $, and hence for the Chern character of $ [ \sigma ( D) ] $: $ \mathop{\rm ch} [ \sigma ( D) ] \in H ^ {*} ( B / S ; \phi ) $. The formula for the topological index of $ D $ now takes the form:
$$ \tag{4 } i _ {t} ( D) = \ ( - 1 ) ^ {n} \{ \mathop{\rm ch} [ \sigma ( D) ] \cdot \pi ^ {*} {\mathcal T} ( M) \} [ T M ] , $$
where $ \pi : T M \rightarrow M $, $ \pi ^ {*} {\mathcal T} ( M) = {\mathcal T} ( T M ) $.
The Thom isomorphism
$$ \phi _ {*} : H ^ {*} ( B / S ) = H ^ {*} ( T M ) \rightarrow H ^ {*} ( M) $$
then enables one to write (4) in the form
$$ \tag{5 } i _ {t} ( D) = \ ( - 1 ) ^ {n ( n + 1 ) / 2 } \{ \phi _ {*} \mathop{\rm ch} [ \sigma ( D) ] \cdot {\mathcal T} ( M) \} [ M ] . $$
(As before, on the right-hand side of (4) and (5) are the values of the corresponding elements on the fundamental cycles, as in (2).)
The topological index is expressed in terms of $ K $- theory as follows. Let $ i : M \rightarrow E $ be a differentiable imbedding of $ M $ in a Euclidean space, $ W $ a tubular neighbourhood of $ M $ in $ E $, which can be regarded as a real vector bundle over $ M $, so that $ T W $ is isomorphic (over $ \mathbf R $) to $ \pi ^ {*} ( W \otimes _ {\mathbf R} \mathbf C ) $, the complexification of $ W $ lifted to $ T M $ by the projection $ \pi : T M \rightarrow M $. Composition of the Thom isomorphism $ \phi : K ( T M ) \rightarrow K ( T W ) $ with the natural homomorphism $ K ( T W ) \rightarrow K ( T E ) $ induced by the imbedding $ W \rightarrow E $ induces a homomorphism $ i _ {!} : K ( T M ) \rightarrow K ( T E ) $. Let $ \beta : K ( T E ) \rightarrow \mathbf Z $ be the Bott periodicity isomorphism. Then the homomorphism $ \beta \circ i _ {!} : K ( T M) \rightarrow \mathbf Z $ does not depend on the imbedding and
$$ i _ {t} ( D) = \beta \circ i _ {!} ( [ \sigma ( D) ] ) . $$
Examples.
3) Let $ M $ be a closed oriented Riemannian manifold, let $ \xi ^ {k} = \wedge ^ {k} ( T ^ {*} M ) \otimes \mathbf C $ be the bundle of complex exterior $ k $- forms over $ M $ and let
$$ d : C ^ \infty ( \xi ^ {k} ) \rightarrow C ^ \infty ( \xi ^ {k+} 1 ) ,\ \ d ^ {*} : C ^ \infty ( \xi ^ {k+} 1 ) \rightarrow C ^ \infty ( \xi ^ {k} ) $$
be the exterior differentiation operator and its adjoint, respectively. The operator
$$ d + d ^ {*} : C ^ \infty ( \xi ^ {e} ) \rightarrow C ^ \infty ( \xi ^ {0} ) , $$
where $ \xi ^ {e} = \oplus _ {p} \xi ^ {2p} $, $ \xi ^ {0} = \oplus _ {p} \xi ^ {2p+} 1 $, is elliptic and the index formula (3) holds for it; furthermore the topological index is equal to the Euler characteristic $ \chi ( M) $( the Hodge–de Rham theorem). For $ \mathop{\rm dim} M = 2 $ the Gauss–Bonnet theorem follows.
4) Let $ \xi ^ \pm $ be the eigen $ ( \pm ) $- spaces of the involution $ I ( \alpha ) = i ^ {p ( p - 1 ) + k } \star \alpha $, $ \alpha \in \xi ^ {p} $, where $ \star $ is the duality operator determined by the metric on $ M $, $ \mathop{\rm dim} M = 2 k $. The restriction of the operator $ d + d ^ {*} $ to an operator from $ C ^ \infty ( \xi ^ {+} ) $ into $ C ^ \infty ( \xi ^ {-} ) $, called the signature operator $ \delta _ {M} $, is an elliptic operator for which the index formula (3) holds; furthermore, the analytic index is equal to the signature of the manifold $ M $, while the topological index is equal to the $ L $- genus (Hirzebruch's theorem).
5) Let $ \eta $ be a holomorphic vector bundle over the complex compact manifold $ M $, let $ \xi ^ {0,q} $ be the bundle of differential forms of type $ ( 0 , q ) $, let $ \eta \otimes \xi ^ {0,q} $ be the bundle of forms of type $ ( 0 , q ) $ with coefficients in $ \eta $, and let $ \zeta ^ {0,q} $ be the $ \mathbf C $- module of smooth sections of this bundle. Let $ \overline \partial \; : \xi ^ {0,q} \rightarrow \xi ^ {0,q+} 1 $ be the Cauchy–Riemann–Dolbeault operator, $ \overline \partial \; {} ^ {*} $ its adjoint, and let $ \xi ^ {e} = \oplus _ {p} \xi ^ {0,2p} $, $ \xi ^ {0} = \oplus _ {p} \xi ^ {0,2p+} 1 $. Then the operator $ \overline \partial \; + \overline \partial \; {} ^ {*} : \xi ^ {e} \rightarrow \xi ^ {0} $ is an elliptic operator for which (3) holds; furthermore, the analytic index is equal to the Euler characteristic of $ M $ with coefficients in the sheaf of germs of holomorphic sections of $ \eta $, while the topological index is $ \{ \mathop{\rm ch} \eta \cdot {\mathcal T} ( M) \} [ M ] $, where $ \mathop{\rm ch} \eta $ is the Chern character of $ \eta $ and $ {\mathcal T} ( M) $ is the Todd class of the tangent bundle to $ M $( the Riemann–Roch–Hirzebruch theorem).
Elliptic complexes.
In the more general situation which arises naturally, for example, in differential geometry, instead of a single operator $ D $ one considers a complex of (pseudo-differential) operators
$$ A : 0 \rightarrow C ^ \infty ( \xi _ {0} ) \mathop \rightarrow \limits ^ { {D _ {0} }} C ^ \infty ( \xi _ {1} ) \mathop \rightarrow \limits ^ { {D _ {1} }} \dots \rightarrow ^ { {D _ N-} 1 } C ^ \infty ( \xi _ {N} ) \rightarrow 0 , $$
where the $ \xi _ {j} $ are differentiable vector bundles over the closed manifold $ M $ and $ D _ {j+} 1 D _ {j} = 0 $. By the symbol of the complex $ A $ one means the corresponding sequence of principal symbols
$$ \sigma ( A) : 0 \rightarrow \ \pi ^ {*} ( \xi _ {0} ) \rightarrow ^ { {\sigma _ 0} } \pi ^ {*} ( \xi _ {1} ) \rightarrow ^ { {\sigma _ 1} } {} \dots \rightarrow ^ { {\sigma _ N-} 1 } \pi ^ {*} ( \xi _ {N} ) \rightarrow 0 , $$
where $ \pi ^ {*} ( \xi _ {j} ) $ is the lifting of $ \xi _ {j} $ to $ S ( M) $ by the projection $ \pi : T ^ {*} M \rightarrow M $. The complex $ A $ is called elliptic if its symbol is an acyclic complex, that is, if it is exact everywhere outside the zero section. By the analytic index of the complex $ A $ one means its Euler characteristic:
$$ i _ {a} ( A) = \chi ( A) = \ \sum _ { j= } 0 ^ { N } ( - 1 ) ^ {j} \mathop{\rm dim} H ^ {j} ( A) , $$
where $ H ^ {j} ( A) $ is the $ j $- th cohomology group of $ A $. Two important examples of elliptic complexes are the de Rham complex and its complex analogue, the Dolbeault complex. The problem of computing $ \chi ( A) $ in terms of the class of the complex $ \sigma ( A) $ in $ K ( T M ) $ can be reduced to computing the index for a single operator [3].
If a compact group $ G $ acts on $ A $( and commutes with the action of $ D _ {j} $, that is, $ A $ is a $ G $- complex), then $ H ^ {j} ( A) $ is a $ G $- module, and $ \chi ( A) $ is defined as an element of the ring of characters of the group $ G $. This is a function in $ C ^ \infty ( G) $. Here it turns out that the index theorem can be regarded as a generalization of the Lefschetz theorem on fixed points, since the topological index at a point $ g \in G $ can be expressed in terms of the index of the restriction of the symbol to the subset $ M ^ {g} \subset M $ of fixed points of the mapping defined by $ g $.
Let $ G $ be a topological cyclic group, that is, there exists an element $ g $ in $ G $ whose powers are dense in $ G $, let $ N ^ {g} $ be the normal bundle to $ M ^ {g} $ in $ M $ and let $ [ \sigma ( S) ] \in K _ {G} ( T M ) $ be the class of the symbol of $ A $. Let $ i ^ {*} [ \sigma ( A)] ( g) \in K _ {G} ( T M ^ {g} ) $ be its restriction and let $ \lambda _ {-} 1 ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) ( g) $ be the class generated by the standard complex of exterior powers of the bundle $ \pi ^ {*} ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) $ to $ M ^ {g} $( here $ i : M ^ {g} \rightarrow M $, $ \pi : T M ^ {g} \rightarrow M ^ {g} $). Then the Lefschetz number $ L ( g , A ) $, which is equal to $ \Sigma ( - 1 ) ^ {j} \mathop{\rm Tr} ( g \mid H ^ {j} ( A) ) $, is given by the formula
$$ L ( g , A ) = \ \mathop{\rm ind} \left \{ \frac{i ^ {*} [ \sigma ( A) ] ( g) }{\lambda _ {-} 1 ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) ( g) } \right \} = \ \mathop{\rm ind} _ {G} A ( g) , $$
where $ \mathop{\rm ind} : K ( T M ^ {g} ) \otimes \mathbf C \rightarrow \mathbf C $ is the natural extension of the topological index $ K ( T M ^ {g} ) \rightarrow \mathbf Z $. The cohomological version of this formula is given by:
$$ \tag{6 } \mathop{\rm ind} _ {G} A ( g) = \ \left \{ \frac{ \mathop{\rm ch} i ^ {*} [ \sigma ( A) ] ( g) }{ \mathop{\rm ch} \lambda _ {-} 1 ( N ^ {g} \otimes _ {\mathbf R} \mathbf C ) ( g) } \ \cdot \pi ^ {*} {\mathcal T} ( M ^ {g} ) \right \} [ M ] . $$
Without the compactness condition on $ G $, but under the hypothesis that $ M ^ {g} $ is a zero-dimensional submanifold and that the action of $ G $ is non-degenerate (that is, the graph of $ g $ is transversal to the diagonal in $ M \times M $), there is an analogous formula, which can be expressed as follows. If $ P \in M ^ {g} $, then $ d g ( P) $ leaves $ T M \mid _ {P} $ fixed while $ g $ induces a linear mapping $ l _ {j} ( g , P ) $ on the fibres $ \xi _ {j} \mid _ {P} $, and
$$ \mathop{\rm ind} _ {G} A ( g) = \ \sum _ {P \in M ^ {g} } \sum _ { j } ( - 1 ) ^ {j} \frac{ \mathop{\rm Tr} l _ {j} ( g , P ) }{ \mathop{\rm det} ( 1 - d g ( P) ) } . $$
Finally, it is possible to weaken the condition of ellipticity of the $ G $- complex $ A $ by considering so-called transversally-elliptic complexes; in this case, the index turns out to be a generalized function on the group $ G $( see [8]). In particular, if $ G $ is finite, then transversal ellipticity is to equivalent to ellipticity, so that the previous formulas are applicable. If $ M = G / H $ is a homogeneous space, then all the complexes of operators are transversally elliptic and in this case the index formula is in essence the same as the Frobenius reciprocity formula for the induced representations of the group $ G $.
Non-Fredholm operators.
In this case it is also sometimes possible to give another definition of the analytic index and to obtain corresponding index formulas.
Examples.
6) Let $ D $ be a uniformly-elliptic operator on $ \mathbf R ^ {n} $ with almost-periodic coefficients. The analytic index $ i _ {a} ( D) $ is introduced by means of the relative dimension in the $ \textrm{ II } _ \infty $- factor (see von Neumann algebra) and is a real number (see [11]). There is a formula analogous to (1), but instead of the integral over $ \mathbf R ^ {n} $ the average value of the almost-periodic function is used.
7) Suppose that a discrete group $ \Gamma $ acts freely on a manifold $ M $ and that the quotient space $ \widetilde{M} = M / \Gamma $ is compact; let $ \xi $, $ \eta $ be vector bundles over $ M $ and let $ \Gamma $ act on them in accordance with its action on $ M $. The analytic index of an elliptic operator $ D : C ^ \infty ( \xi ) \rightarrow C ^ \infty ( \eta ) $ on $ M $ commuting with the action of $ \Gamma $ is defined by the formula
$$ \tag{7 } i _ {a} ( D) = \ \mathop{\rm Tr} _ \Gamma P _ {1} - \mathop{\rm Tr} _ \Gamma P _ {2} , $$
where $ P _ {1} $, $ P _ {2} $ are the orthogonal projections on $ \mathop{\rm Ker} D $ and $ \mathop{\rm Ker} D ^ {*} $ in $ L _ {2} ( M , d \mu ) $, $ d \mu $ is any $ \Gamma $- invariant smooth density on $ M $ and $ \mathop{\rm Tr} _ \Gamma P $ is defined, for any operator $ P $ commuting with $ \Gamma $ and having smooth kernel $ P ( x , y ) $, by the formula
$$ \mathop{\rm Tr} _ \Gamma P = \ \int\limits _ {M _ {0} } \mathop{\rm tr} P ( x , x ) d \mu $$
(here $ M _ {0} $ is any fundamental domain of the group $ \Gamma $ on $ M $ and $ \mathop{\rm tr} $ is the trace of the matrix). It turns out that $ i _ {a} ( D) = i _ {a} ( \widetilde{D} ) $, where $ \widetilde{D} $ is the operator on $ \widetilde{M} $ whose symbol $ \widetilde \sigma ( D) $ induces $ \sigma ( D) $ under the lifting to $ M $ by the canonical projection $ \pi : M \rightarrow \widetilde{M} $[12]. Thus, the index formula for the operator $ D $ can be obtained from the index formula for the operator $ \widetilde{D} $ on the compact manifold $ \widetilde{M} $. This result enables one to reveal the non-triviality of spaces in which representations of discrete series are realized [13].
A formula of the same type can be obtained for invariant elliptic operators on homogeneous spaces of Lie groups, even without $ \Gamma $ being discrete, with a natural generalization of the analytic index [20].
Another generalization of this situation can be obtained if one considers invariant operators on a manifold $ M $ with an action of a locally compact group $ G $ such that $ M / G $ is compact [24].
8) If the coefficients of a uniformly-elliptic operator $ D $ on $ \mathbf R ^ {n} $ form a homogeneous measurable random field, then it is possible to introduce the analytic index $ i _ {a} ( D) $, which is a random variable (in the ergodic case, a real number) defined by formula (7) with $ \mathop{\rm Tr} _ \Gamma P $ replaced by $ \mathop{\rm Tr} P $. Here $ \mathop{\rm Tr} P $ is constructed from the kernel $ P ( x , y ) $ of the operator $ P $ by averaging over $ x $: $ \mathop{\rm Tr} P = M _ {x} \{ \mathop{\rm tr} P ( x , x ) \} $. This example is a generalization of Example 6) and an analogous index formula holds for it .
9) Let $ M $ be a compact manifold with a foliation $ {\mathcal F} $ and $ D $ a longitudinal elliptic differential operator on $ M $, i.e. a differential operator containing only differentiations along the leaves and elliptic on every leaf. Suppose that there is a transverse measure on $ {\mathcal F} $. Then a real-valued analytic index of $ D $ can be defined and a formula of Atiyah–Singer type can be proved. Considering measured foliations, in this context one comes to a formula which generalizes that of Example 8), [18], [19].
Index formulas with values in $ K $-groups.
10) If a family of elliptic operators is given, parametrized by the points $ y $ of a compact space $ Y $, then its analytic index $ i _ {a} ( D) \in K ( Y) $ has been defined (see [15]). The topological index $ i _ {t} ( D) $ is constructed by analogy with formula (6) (all the constructions are carried out "fibrewise" over $ Y $) and the index theorem holds.
11) A more general theorem is obtained if one considers elliptic operators over a compact manifold acting in sections of vector bundles with fibres which are finitely-generated projective modules over a fixed $ C ^ {*} $- algebra $ {\mathcal A} $. The analytic index here takes values in the group $ K ^ {0} ( {\mathcal A} ) $. If one takes $ {\mathcal A} = C ( Y) $ with a compact $ Y $, then one obtains the formula of Example 10). Also the equivalent situation (with a compact Lie group $ G $) can be considered in this context [26], [29].
The case when $ A $ is a $ \textrm{ II } _ {1} $- factor is of particular interest [28], implying the formula of Example 7).
12) There is a number of generalizations of the Atiyah–Singer formulas with the analytic index taking values in homology $ K $- groups or bivariant Kasparov $ K $- groups. Taking the Chern character and applying some kind of intersection index usually allows one to pass to the usual number-valued index formulas [23], [25]. Also, the longitudinal index theorem of Example 9) can be generalized in this manner [21].
13) Consider two generalized Dirac operators $ D _ {0} $, $ D _ {1} $ which coincide near infinity (in particular, they are defined on Riemannian manifolds $ M _ {0} $, $ M _ {1} $ which coincide near infinity, i.e. $ M _ {0} \setminus K _ {0} $ and $ M _ {1} \setminus K _ {1} $ are isometric for some compact subsets $ K _ {j} \subset M _ {j} $, $ j = 1 , 2 $). Let $ D _ {0} $, $ D _ {1} $ be positive near infinity and let there be the natural splittings
$$ D _ {j} = \left ( \begin{array}{cc} 0 &{D _ {j} ^ {-} } \\ {D _ {j} ^ {+} } & 0 \\ \end{array} \right ) ,\ \ j = 1 , 2 . $$
Then $ \mathop{\rm ind} D _ {1} ^ {+} - \mathop{\rm ind} D _ {0} ^ {+} $ can be expressed by a formula of Atiyah–Singer type having important geometrical applications [22].
New analytic tools.
The Atiyah–Bott formula
$$ \mathop{\rm ind} D = \mathop{\rm Tr} \mathop{\rm exp} ( - t D ^ {*} D ) - \mathop{\rm Tr} \mathop{\rm exp} ( - t D D ^ {*} ) $$
provides a local expression of the index if one uses the asymptotic expansion of the traces on the right-hand side as $ t \downarrow 0 $. But this expression contains lower-order terms of the symbol of $ D $, so it seems difficult to see how the corresponding integrals cancel. It occurred that cancellation is obtained by using some symmetry and supersymmetry arguments. Also a probabilistic approach is effective to work with the traces of heat kernels. Families of elliptic operators can be considered in this way too [30]–[42].
References
| [1] | I.M. Gel'fand, "On elliptic differential equations" Russian Math. Surveys , 15 : 3 (1960) pp. 113–123 Uspekhi Mat. Nauk , 15 : 3 (1960) pp. 121–132 |
| [2] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators on compact manifolds" Bull. Amer. Math. Soc. , 69 (1963) pp. 422–433 MR0157392 Zbl 0118.31203 |
| [3] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" Ann. of Math. , 87 (1968) pp. 484–530 MR0236950 MR0232402 Zbl 0164.24001 |
| [4] | M.F. Atiyah, G.B. Segal, "The index of elliptic operators II" Ann. of Math. , 87 (1968) pp. 531–545 MR0236953 MR0236951 Zbl 0164.24201 |
| [5] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators III" Ann. of Math. , 87 (1968) pp. 546–604 MR0236952 Zbl 0164.24301 |
| [6] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators IV" Ann. of Math. , 93 (1971) pp. 119–138 MR0279833 Zbl 0212.28603 |
| [7] | B.V. Fedosov, "Analytic formulas for the index of elliptic operators" Trans. Moscow Math. Soc. , 30 (1974) pp. 279–330 Trudy Moskov. Mat. Obshch. , 30 (1974) pp. 159–241 MR0420731 Zbl 0349.58006 |
| [8] | M.F. Atiyah, "Elliptic operators and compact groups" , Lect. notes in math. , 401 , Springer (1974) MR0482866 Zbl 0297.58009 |
| [9] | R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) MR0198494 Zbl 0137.17002 |
| [10a] | M.F. Atiyah, R. Bott, V.K. Patodi, "On the heat equation and the index theorem" Invent. Math. , 19 (1973) pp. 279–330 MR0650828 Zbl 0364.58016 Zbl 0257.58008 |
| [10b] | M.F. Atiyah, R. Bott, V.K. Patodi, "Errata to "On the heat equation and the index theorem" " Invent. Math. , 28 (1975) pp. 277–280 MR0650829 Zbl 0301.58018 |
| [11] | L. Coburn, R. Moyer, I.M. Singer, "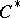 -algebras of almost-periodic pseudo-differential operators" Acta Math. , 130 : 3–4 (1973) pp. 279–307 MR0415407 Zbl 0263.47042 -algebras of almost-periodic pseudo-differential operators" Acta Math. , 130 : 3–4 (1973) pp. 279–307 MR0415407 Zbl 0263.47042 |
| [12] | M.F. Atiyah, "Elliptic operators, discrete groups and von Neumann algebras" Astérisque , 32–33 (1976) pp. 43–72 MR0420729 Zbl 0323.58015 |
| [13] | M.F. Atiyah, W. Schmid, "A geometric construction of the discrete series for semisimple Lie groups" Invent. Math. , 42 (1977) pp. 1–62 MR0463358 Zbl 0373.22001 |
| [14a] | B.V. Fedosov, M.A. Shubin, "The index of random elliptic operators I" Math. USSR Sb. , 34 (1978) pp. 671–699 Mat. Sb. , 106 : 1 pp. 108–140 MR0501190 Zbl 0448.47033 |
| [14b] | B.V. Fedosov, M.A. Shubin, "The index of random elliptic operators II" Math. USSR Sb. , 35 (1979) pp. 131–156 Mat. Sb. , 106 : 3 pp. 455–483 MR0501191 Zbl 0422.58025 |
| [15] | M.F. Atiyah, "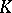 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [16] | L. Boutet de Monvel, "Boundary problems for pseudodifferential operators" Acta Math. , 126 : 1–2 (1971) pp. 11–51 |
| [17a] | B.V. Fedosov, "The analytic formula for the index of an elliptic boundary value problem" Mat. USSR Sb. , 22 (1974) pp. 61–90 Mat. Sb. , 93 : 1 (1974) pp. 62–89 Zbl 0385.58009 Zbl 0323.58016 Zbl 0337.58007 |
| [17b] | B.V. Fedosov, "An analytic formula for the index of an elliptic boundary value problem II" Mat. USSR Sb. , 24 (1974) pp. 511–535 Mat. Sb. , 95 : 4 (1974) pp. 525–550 MR0383464 Zbl 0323.58016 |
| [17c] | B.V. Fedosov, "An analytic formula for the index of an elliptic boundary value problem III" Mat. USSR Sb. , 30 (1976) pp. 341–359 Mat. Sb. , 101 : 3 (1976) pp. 380–401 MR448451 Zbl 0385.58009 |
| [18] | A. Connes, "Sur la théorie non commutative de l'intégration" , Algèbres d'opérateurs , Lect. notes in math. , 725 , Springer (1979) pp. 19–143 MR0548112 Zbl 0412.46053 |
| [19] | A. Connes, "A survey of foliations and operator algebras" , Operator algebras and applications , Proc. Symp. Pure Math. , 38 : 1 , Amer. Math. Soc. (1982) pp. 521–628 MR0679730 Zbl 0531.57023 |
| [20] | A. Connes, H. Moscovici, "The  -index theorem for homogeneous spaces of Lie groups" Ann. of Math. , 115 (1982) pp. 291–330 MR647808 -index theorem for homogeneous spaces of Lie groups" Ann. of Math. , 115 (1982) pp. 291–330 MR647808 |
| [21] | A. Connes, G. Skandalis, "The longitudinal index theorem for foliations" Publ. Res. Inst. Math. Sci. Kyoto Univ. , 20 (1984) pp. 1139–1183 MR0775126 Zbl 0575.58030 |
| [22] | M. Gromov, H.B. Lawson, "Positive scalar curvature and the Dirac operator on complete Riemannian manifolds" Publ. Math. IHES , 58 (1983) pp. 83–196 MR0720933 Zbl 0538.53047 |
| [23] | G.G. Kasparov, "Topological invariants of elliptic operators I.  -homology" Math. USSR Izv. , 9 (1975) pp. 751–792 Izv. Akad. Nauk SSSR, Ser. Mat. , 39 (1975) pp. 796–838 MR488027 -homology" Math. USSR Izv. , 9 (1975) pp. 751–792 Izv. Akad. Nauk SSSR, Ser. Mat. , 39 (1975) pp. 796–838 MR488027 |
| [24] | G.G. Kasparov, "An index of invariant elliptic operators, 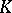 -theory, and representations of Lie groups" Soviet Math. Dokl. , 27 (1983) pp. 105–109 Dokl. Akad. Nauk SSSR , 268 (1983) pp. 533–537 MR691088 -theory, and representations of Lie groups" Soviet Math. Dokl. , 27 (1983) pp. 105–109 Dokl. Akad. Nauk SSSR , 268 (1983) pp. 533–537 MR691088 |
| [25] | G.G. Kasparov, "Operator 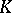 -theory and its applications: elliptic operators, group representation, higher signatures, -theory and its applications: elliptic operators, group representation, higher signatures, 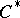 -extensions" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , PWN & Elsevier (1984) pp. 987–1000 MR804752 -extensions" , Proc. Internat. Congress Mathematicians (Warszawa, 1983) , PWN & Elsevier (1984) pp. 987–1000 MR804752 |
| [26] | A.S. [A.S. Mishchenko] Miščenko, A.T. Fomenko, "The index of elliptic operators over 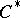 -algebras" Math. USSR Izv. , 15 (1980) pp. 87–112 Izv. Akad. Nauk SSSR, Ser. Mat. , 43 (1979) pp. 831–851 -algebras" Math. USSR Izv. , 15 (1980) pp. 87–112 Izv. Akad. Nauk SSSR, Ser. Mat. , 43 (1979) pp. 831–851 |
| [27] | S. Rempel, B.-W. Schulze, "Index theory of elliptic boundary problems" , Akademie Verlag (1982) MR0690065 Zbl 0504.35002 |
| [28] | I.M. Singer, "Some remarks on operator theory and index theory" , 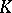 -theory and operator algebras , Lect. notes in math. , 757 , Springer (1977) pp. 128–138 MR0467848 Zbl 0444.47040 -theory and operator algebras , Lect. notes in math. , 757 , Springer (1977) pp. 128–138 MR0467848 Zbl 0444.47040 |
| [29] | E.V. Troitskii, "The equivariant index of 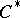 -elliptic operators" Math. USSR Izv. , 29 (1987) pp. 207–224 Izv. Akad. Nauk SSSR, Ser. Mat. , 50 (1986) pp. 849–965 -elliptic operators" Math. USSR Izv. , 29 (1987) pp. 207–224 Izv. Akad. Nauk SSSR, Ser. Mat. , 50 (1986) pp. 849–965 |
| [30] | L. Alvarez-Gaumé, "Supersymmetry and the Atiyah–Singer index theorem" Commun. Math. Phys. , 90 (1983) pp. 161–173 Zbl 0528.58034 |
| [31] | D. Quillen, "Superconnections and the Chern character" Topology , 24 (1985) pp. 89–95 MR0790678 Zbl 0569.58030 |
| [32] | N. Berline, M. Vergne, "A computation of the equivariant index of the Dirac operator" Bull. Soc. Math. France , 113 (1985) pp. 305–345 MR0834043 Zbl 0592.58044 |
| [33] | N. Berline, M. Vergne, "A proof of Bismut local index theorem for a family of Dirac operators" Topology , 26 (1987) pp. 435–464 MR0919729 Zbl 0636.58030 |
| [34] | J.-M. Bismut, "The Atiyah–Singer theorem: A probabilistic approach I. The index theorem" J. Funct. Anal. , 57 (1984) pp. 56–98 MR0744920 MR0756173 |
| [35] | J.-M. Bismut, "Localization formulas, superconnections, and the index theorem for families" Commun. Math. Phys. , 103 (1986) pp. 127–166 MR0826861 Zbl 0602.58042 |
| [36] | J.-M. Bismut, "The Atiyah–Singer index theorem for families of Dirac operators: two heat equation proofs" Invent. Math. , 83 (1986) pp. 91–151 MR0813584 Zbl 0592.58047 |
| [37] | H. Donnelly, "Local index theorem for families" Michigan Math. J. , 35 (1988) pp. 11–20 MR0931936 Zbl 0657.58039 |
| [38] | E. Getzler, "Pseudodifferential operators on supermanifolds and the Atiyah–Singer index theorem" Commun. Math. Phys. , 92 (1983) pp. 163–178 MR0728863 Zbl 0543.58026 |
| [39] | E. Getzler, "A short proof of the local Atiyah–Singer index theorem" Topology , 25 (1988) pp. 111–117 MR0836727 Zbl 0607.58040 |
| [40] | P. Gilkey, "Invariance theory, the heat equation and the Atiyah–Singer theorem" , Publish or Perish (1984) MR783634 Zbl 0565.58035 |
| [41] | R. Léandre, "Sur le théorème d'Atiyah–Singer" Probab. Theory Related Fields , 80 (1988) pp. 119–137 MR970474 |
| [42] | R. Léandre, "Sur le théorème de l'indice des familles" , Sem. Probab. Strasbourg XII , Lect. notes in math. , 1321 , Springer (1988) pp. 348–413 MR0960536 |
Comments
Several new proofs of the Atiyah–Singer index theorem have been given in recent years.
In his paper [a5], E. Witten suggested that supersymmetric quantum theory might provide the framework for a simple proof of the index theorem. Such a proof was realized by L. Alvarez-Gaumé [30] and subsequently by Friedan and Windey [a4]. These theoretical physicists relied on formal manipulations inside path integrals (including fermionic path integrals). So their proofs were certainly not rigorous. E. Getzler [38] found a rigorous version of their arguments which relied on pseudo-differential operator theory and the theory of supermanifolds. More recently, Getzler [39] found a proof whose geometric and algebraic parts are elementary and transparent. Independent of this work J.-M. Bismut [34] found a related proof using probabilistic methods.
For further material cf. also [a2], Chapt. XIX, [a1], Chapt. 12 and [a3], Chapt. 9.
References
| [a1] | H.L. Cycon, R.G. Froese, W. Kirsch, B. Simon, "Schrödinger operators" , Springer (1987) MR0883643 Zbl 0619.47005 |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , III. Pseudo-differential operators , Springer (1985) MR1540773 MR0781537 MR0781536 Zbl 0612.35001 Zbl 0601.35001 |
| [a3] | M. Kaku, "Introduction to superstrings" , Springer (1988) MR0954610 Zbl 0655.58001 |
| [a4] | D. Friedan, P. Windey, "Supersymmetric derivation of the Atiyah–Singer index theorem and the chiral anomaly" Nucl. Phys. , B253 (1984) pp. 395–416 MR888706 |
| [a5] | E. Witten, "Supersymmetry and Morse theory" J. Diff. Geom. , 17 (1982) pp. 661–692 MR0683171 Zbl 0499.53056 |
Index formulas. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Index_formulas&oldid=18079