Difference between revisions of "Unimodular element"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | u0953401.png | ||
| + | $#A+1 = 21 n = 1 | ||
| + | $#C+1 = 21 : ~/encyclopedia/old_files/data/U095/U.0905340 Unimodular element, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''unimodular vector'' | ''unimodular vector'' | ||
| − | Let | + | Let $ R $ |
| + | be a ring with unit and $ M $ | ||
| + | a right module over $ R $. | ||
| + | An element $ x $ | ||
| + | in $ M $ | ||
| + | is called unimodular if $ \mathop{\rm ann} _ {R} ( x) = \{ {r \in R } : {xr = 0 } \} = 0 $ | ||
| + | and the submodule $ \langle x \rangle $ | ||
| + | generated by $ x $ | ||
| + | has a complement $ N $ | ||
| + | in $ M $, | ||
| + | i.e. there is a submodule $ N \subset M $ | ||
| + | such that $ \langle x \rangle \cap N = \{ 0 \} $, | ||
| + | $ \langle x \rangle + N = M $, | ||
| + | so that $ \langle x \rangle \oplus N = M $. | ||
| − | An element of a free module | + | An element of a free module $ M $ |
| + | that is part of a basis of $ M $ | ||
| + | is unimodular. An element $ x \in M $ | ||
| + | is unimodular if and only if there is a homomorphism of modules $ \rho : M \rightarrow R $ | ||
| + | such that $ \rho ( x) = 1 $. | ||
| + | A row (or column) of a [[Unimodular matrix|unimodular matrix]] over $ R $ | ||
| + | is unimodular. The question when the converse is true is important in [[Algebraic K-theory|algebraic $ K $- | ||
| + | theory]]. Cf. also [[Stable rank|Stable rank]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.J. Hahn, O.T. O'Meara, "The classical groups and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095340/u09534022.png" />-theory" , Springer (1989) pp. 9, §141ff {{MR|1007302}} {{ZBL|}} </TD></TR></table> |
Latest revision as of 08:27, 6 June 2020
unimodular vector
Let $ R $ be a ring with unit and $ M $ a right module over $ R $. An element $ x $ in $ M $ is called unimodular if $ \mathop{\rm ann} _ {R} ( x) = \{ {r \in R } : {xr = 0 } \} = 0 $ and the submodule $ \langle x \rangle $ generated by $ x $ has a complement $ N $ in $ M $, i.e. there is a submodule $ N \subset M $ such that $ \langle x \rangle \cap N = \{ 0 \} $, $ \langle x \rangle + N = M $, so that $ \langle x \rangle \oplus N = M $.
An element of a free module $ M $ that is part of a basis of $ M $ is unimodular. An element $ x \in M $ is unimodular if and only if there is a homomorphism of modules $ \rho : M \rightarrow R $ such that $ \rho ( x) = 1 $. A row (or column) of a unimodular matrix over $ R $ is unimodular. The question when the converse is true is important in algebraic $ K $- theory. Cf. also Stable rank.
References
| [a1] | A.J. Hahn, O.T. O'Meara, "The classical groups and 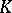 -theory" , Springer (1989) pp. 9, §141ff MR1007302 |
How to Cite This Entry:
Unimodular element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unimodular_element&oldid=17441
Unimodular element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unimodular_element&oldid=17441