|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
| | + | <!-- |
| | + | p0751601.png |
| | + | $#A+1 = 110 n = 0 |
| | + | $#C+1 = 110 : ~/encyclopedia/old_files/data/P075/P.0705160 Projective algebra |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | + | |
| | + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | + | |
| | ''in the narrow sense'' | | ''in the narrow sense'' |
| | | | |
| − | An algebra of points on a projective line; projectively-invariant constructions for defining addition and multiplication of points on a projective line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751601.png" />, lying in a projective plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751602.png" /> for which the [[Desargues assumption|Desargues assumption]] holds. These constructions depend on the choice of three distinct points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751603.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751604.png" />. | + | An algebra of points on a projective line; projectively-invariant constructions for defining addition and multiplication of points on a projective line $ l $, |
| | + | lying in a projective plane $ \pi $ |
| | + | for which the [[Desargues assumption|Desargues assumption]] holds. These constructions depend on the choice of three distinct points $ O, E, U $ |
| | + | on $ l $. |
| | | | |
| | ===Construction I=== | | ===Construction I=== |
| − | determines for any two points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751605.png" /> different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751606.png" /> a third point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751607.png" />, also different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751608.png" /> and called the sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p0751609.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516010.png" />. One draws in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516011.png" /> three straight lines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516012.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516014.png" />, different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516015.png" />, forming a triangle and passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516018.png" />, respectively. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516019.png" /> be the point of intersection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516021.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516022.png" /> be that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516025.png" /> that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516027.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516028.png" /> that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516030.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516031.png" /> intersects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516032.png" /> in the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516033.png" /> (for the general case see Fig. a). It turns out that the point thus constructed depends on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516034.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516035.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516036.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516037.png" /> only, and not on the choice of the straight lines or the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516038.png" />. | + | determines for any two points $ A, B $ |
| | + | different from $ U $ |
| | + | a third point $ A + B $, |
| | + | also different from $ U $ |
| | + | and called the sum of $ A $ |
| | + | and $ B $. |
| | + | One draws in $ \pi $ |
| | + | three straight lines $ a $, |
| | + | $ b $ |
| | + | and $ u $, |
| | + | different from $ l $, |
| | + | forming a triangle and passing through $ A $, |
| | + | $ B $ |
| | + | and $ U $, |
| | + | respectively. Let $ P $ |
| | + | be the point of intersection of $ u $ |
| | + | and $ a $, |
| | + | let $ Q $ |
| | + | be that of $ u $ |
| | + | and $ b $, |
| | + | $ R $ |
| | + | that of $ OQ $ |
| | + | and $ a $, |
| | + | and $ S $ |
| | + | that of $ b $ |
| | + | and $ UR $. |
| | + | Then $ PS $ |
| | + | intersects $ l $ |
| | + | in the point $ T = A + B $( |
| | + | for the general case see Fig. a). It turns out that the point thus constructed depends on $ A $, |
| | + | $ B $, |
| | + | $ O $, |
| | + | and $ U $ |
| | + | only, and not on the choice of the straight lines or the point $ E $. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p075160a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p075160a.gif" /> |
| Line 11: |
Line 59: |
| | | | |
| | ===Construction II=== | | ===Construction II=== |
| − | determines for any two points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516039.png" /> different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516040.png" /> a third point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516041.png" />, also different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516042.png" /> and called the product of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516044.png" />. One draws in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516045.png" /> three straight lines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516047.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516048.png" />, different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516049.png" />, forming a triangle and passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516050.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516051.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516052.png" />, respectively. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516053.png" /> be the point of intersection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516055.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516056.png" /> be that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516057.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516059.png" /> that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516060.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516061.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516062.png" /> that of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516063.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516064.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516065.png" /> intersects <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516066.png" /> in the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516067.png" /> (for the general case see Fig. b). It turns out that the point thus constructed depends on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516068.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516069.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516070.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516071.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516072.png" /> only, and not on the choice of the straight lines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516073.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516074.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516075.png" />. The points of the line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516076.png" /> (distinct from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516077.png" />) form a [[Skew-field|skew-field]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516078.png" /> under these operations of addition and multiplication. Interchanging <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516079.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516080.png" /> in construction II leads to an anti-isomorphic skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516081.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516082.png" /> is another triple of points on a straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516083.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516084.png" />, then the corresponding skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516085.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516086.png" />, since there is a projective correspondence between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516087.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516088.png" />. Therefore, any skew-field isomorphic to it is simply called a skew-field of the given projective plane (or even of the given projective geometry). One also says that one has a projective geometry over the skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516089.png" />. In the general cases of constructions I and II there figure four points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516090.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516091.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516092.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516093.png" />, lying in one plane and no three of which are collinear; these form a complete quadrangle with three pairs of opposite sides <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516094.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516095.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516096.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516097.png" />; and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516098.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p07516099.png" />. The points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160100.png" /> of intersection of these pairs of opposite sides are called diagonal points, while the straight lines joining diagonal points are called diagonals. A special case, not indicated in the figure, corresponds to the situation that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160101.png" /> are collinear (see [[Fano postulate|Fano postulate]]). | + | determines for any two points $ A, B $ |
| | + | different from $ U $ |
| | + | a third point $ A \cdot B $, |
| | + | also different from $ U $ |
| | + | and called the product of $ A $ |
| | + | and $ B $. |
| | + | One draws in $ \pi $ |
| | + | three straight lines $ a $, |
| | + | $ b $ |
| | + | and $ u $, |
| | + | different from $ l $, |
| | + | forming a triangle and passing through $ A $, |
| | + | $ B $ |
| | + | and $ U $, |
| | + | respectively. Let $ P $ |
| | + | be the point of intersection of $ u $ |
| | + | and $ a $, |
| | + | let $ Q $ |
| | + | be that of $ u $ |
| | + | and $ b $, |
| | + | $ R $ |
| | + | that of $ EQ $ |
| | + | and $ a $, |
| | + | and $ S $ |
| | + | that of $ OR $ |
| | + | and $ b $. |
| | + | Then $ PS $ |
| | + | intersects $ l $ |
| | + | in the point $ T = A \cdot B $( |
| | + | for the general case see Fig. b). It turns out that the point thus constructed depends on $ A $, |
| | + | $ B $, |
| | + | $ O $, |
| | + | $ E $, |
| | + | $ U $ |
| | + | only, and not on the choice of the straight lines $ a $, |
| | + | $ b $ |
| | + | and $ u $. |
| | + | The points of the line $ l $( |
| | + | distinct from $ U $) |
| | + | form a [[Skew-field|skew-field]] $ K ( O, E, U) $ |
| | + | under these operations of addition and multiplication. Interchanging $ A $ |
| | + | and $ B $ |
| | + | in construction II leads to an anti-isomorphic skew-field $ K ^ {*} ( O, E, U) $. |
| | + | If $ O _ {1} , E _ {1} , U _ {1} $ |
| | + | is another triple of points on a straight line $ l _ {1} $ |
| | + | in $ \pi $, |
| | + | then the corresponding skew-field $ K _ {1} ( O _ {1} , E _ {1} , U _ {1} ) $ |
| | + | is isomorphic to $ K ( O, E, U) $, |
| | + | since there is a projective correspondence between $ l $ |
| | + | and $ l _ {1} $. |
| | + | Therefore, any skew-field isomorphic to it is simply called a skew-field of the given projective plane (or even of the given projective geometry). One also says that one has a projective geometry over the skew-field $ K $. |
| | + | In the general cases of constructions I and II there figure four points $ P $, |
| | + | $ Q $, |
| | + | $ R $, |
| | + | $ S $, |
| | + | lying in one plane and no three of which are collinear; these form a complete quadrangle with three pairs of opposite sides $ PQ $, |
| | + | $ RS $; |
| | + | $ PS $, |
| | + | $ QR $; |
| | + | and $ PR $, |
| | + | $ QS $. |
| | + | The points $ X, Y, Z $ |
| | + | of intersection of these pairs of opposite sides are called diagonal points, while the straight lines joining diagonal points are called diagonals. A special case, not indicated in the figure, corresponds to the situation that $ X, Y, Z $ |
| | + | are collinear (see [[Fano postulate|Fano postulate]]). |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p075160b.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p075160b.gif" /> |
| Line 17: |
Line 128: |
| | Figure: p075160b | | Figure: p075160b |
| | | | |
| − | Similar constructions can be carried out in a pencil of straight lines passing through a point, using a complete quadrilateral, a figure dual to a quadrangle, and leading to a skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160102.png" /> anti-isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160103.png" />. | + | Similar constructions can be carried out in a pencil of straight lines passing through a point, using a complete quadrilateral, a figure dual to a quadrangle, and leading to a skew-field $ K ^ {*} $ |
| | + | anti-isomorphic to $ K $. |
| | | | |
| − | The properties of the projective line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160104.png" /> as an algebraic system are determined by the geometric (projectively-invariant) properties of the projective plane in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160105.png" /> lies. E.g., commutativity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160106.png" /> is equivalent to the Pappus axiom being true; Fano's postulate is equivalent to the characteristic of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160107.png" /> being different from 2; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160108.png" /> has no other automorphisms but inner ones, then every [[Projective transformation|projective transformation]] is a [[Collineation|collineation]], etc. | + | The properties of the projective line $ l $ |
| | + | as an algebraic system are determined by the geometric (projectively-invariant) properties of the projective plane in which $ l $ |
| | + | lies. E.g., commutativity of $ K $ |
| | + | is equivalent to the Pappus axiom being true; Fano's postulate is equivalent to the characteristic of $ K $ |
| | + | being different from 2; if $ K $ |
| | + | has no other automorphisms but inner ones, then every [[Projective transformation|projective transformation]] is a [[Collineation|collineation]], etc. |
| | | | |
| − | Using the skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160109.png" /> on the straight line, and hence in the projective space containing the line, one can introduce projective coordinates, giving an algebraic model of the projective space, so that the contents of the projective geometry is, in essence, determined by properties of the same skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075160/p075160110.png" /> over which it is constructed. | + | Using the skew-field $ K $ |
| | + | on the straight line, and hence in the projective space containing the line, one can introduce projective coordinates, giving an algebraic model of the projective space, so that the contents of the projective geometry is, in essence, determined by properties of the same skew-field $ K $ |
| | + | over which it is constructed. |
| | | | |
| | In the wide sense, in projective geometry one studies the set of subspaces of projective space, which is a complemented [[Modular lattice|modular lattice]]. Here one does not require the space to be finite-dimensional, but imposes the condition of completeness, existence of a homogeneous basis, etc. Accordingly, one can establish various connections with the theory of prime and regular rings, the theory of Abelian operator groups and other branches of algebra. | | In the wide sense, in projective geometry one studies the set of subspaces of projective space, which is a complemented [[Modular lattice|modular lattice]]. Here one does not require the space to be finite-dimensional, but imposes the condition of completeness, existence of a homogeneous basis, etc. Accordingly, one can establish various connections with the theory of prime and regular rings, the theory of Abelian operator groups and other branches of algebra. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , '''1''' , Cambridge Univ. Press (1947)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Artin, "Geometric algebra" , Interscience (1957)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , '''1''' , Cambridge Univ. Press (1947) {{MR|0028055}} {{ZBL|0796.14002}} {{ZBL|0796.14003}} {{ZBL|0796.14001}} {{ZBL|0157.27502}} {{ZBL|0157.27501}} {{ZBL|0055.38705}} {{ZBL|0048.14502}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E. Artin, "Geometric algebra" , Interscience (1957) {{MR|1529733}} {{MR|0082463}} {{ZBL|0077.02101}} </TD></TR></table> |
| − | | |
| − | | |
| | | | |
| | ====Comments==== | | ====Comments==== |
| Line 36: |
Line 153: |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.S.M. Coxeter, "The real projective plane" , Cambridge Univ. Press (1961)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968) {{MR|0262046}} {{MR|0229120}} {{ZBL|0153.49601}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Baer, "Linear algebra and projective geometry" , Acad. Press (1952) {{MR|0052795}} {{ZBL|0049.38103}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.S.M. Coxeter, "The real projective plane" , Cambridge Univ. Press (1961) {{MR|1198272}} {{MR|1198271}} {{MR|0112071}} {{MR|0124786}} {{MR|0070189}} {{MR|1570447}} {{MR|0030205}} {{ZBL|0772.51001}} {{ZBL|0086.35805}} {{ZBL|0090.12104}} {{ZBL|0065.36401}} {{ZBL|0032.11302}} </TD></TR></table> |
in the narrow sense
An algebra of points on a projective line; projectively-invariant constructions for defining addition and multiplication of points on a projective line $ l $,
lying in a projective plane $ \pi $
for which the Desargues assumption holds. These constructions depend on the choice of three distinct points $ O, E, U $
on $ l $.
Construction I
determines for any two points $ A, B $
different from $ U $
a third point $ A + B $,
also different from $ U $
and called the sum of $ A $
and $ B $.
One draws in $ \pi $
three straight lines $ a $,
$ b $
and $ u $,
different from $ l $,
forming a triangle and passing through $ A $,
$ B $
and $ U $,
respectively. Let $ P $
be the point of intersection of $ u $
and $ a $,
let $ Q $
be that of $ u $
and $ b $,
$ R $
that of $ OQ $
and $ a $,
and $ S $
that of $ b $
and $ UR $.
Then $ PS $
intersects $ l $
in the point $ T = A + B $(
for the general case see Fig. a). It turns out that the point thus constructed depends on $ A $,
$ B $,
$ O $,
and $ U $
only, and not on the choice of the straight lines or the point $ E $.
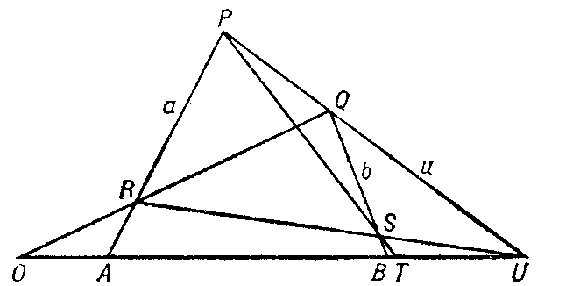
Figure: p075160a
Construction II
determines for any two points $ A, B $
different from $ U $
a third point $ A \cdot B $,
also different from $ U $
and called the product of $ A $
and $ B $.
One draws in $ \pi $
three straight lines $ a $,
$ b $
and $ u $,
different from $ l $,
forming a triangle and passing through $ A $,
$ B $
and $ U $,
respectively. Let $ P $
be the point of intersection of $ u $
and $ a $,
let $ Q $
be that of $ u $
and $ b $,
$ R $
that of $ EQ $
and $ a $,
and $ S $
that of $ OR $
and $ b $.
Then $ PS $
intersects $ l $
in the point $ T = A \cdot B $(
for the general case see Fig. b). It turns out that the point thus constructed depends on $ A $,
$ B $,
$ O $,
$ E $,
$ U $
only, and not on the choice of the straight lines $ a $,
$ b $
and $ u $.
The points of the line $ l $(
distinct from $ U $)
form a skew-field $ K ( O, E, U) $
under these operations of addition and multiplication. Interchanging $ A $
and $ B $
in construction II leads to an anti-isomorphic skew-field $ K ^ {*} ( O, E, U) $.
If $ O _ {1} , E _ {1} , U _ {1} $
is another triple of points on a straight line $ l _ {1} $
in $ \pi $,
then the corresponding skew-field $ K _ {1} ( O _ {1} , E _ {1} , U _ {1} ) $
is isomorphic to $ K ( O, E, U) $,
since there is a projective correspondence between $ l $
and $ l _ {1} $.
Therefore, any skew-field isomorphic to it is simply called a skew-field of the given projective plane (or even of the given projective geometry). One also says that one has a projective geometry over the skew-field $ K $.
In the general cases of constructions I and II there figure four points $ P $,
$ Q $,
$ R $,
$ S $,
lying in one plane and no three of which are collinear; these form a complete quadrangle with three pairs of opposite sides $ PQ $,
$ RS $;
$ PS $,
$ QR $;
and $ PR $,
$ QS $.
The points $ X, Y, Z $
of intersection of these pairs of opposite sides are called diagonal points, while the straight lines joining diagonal points are called diagonals. A special case, not indicated in the figure, corresponds to the situation that $ X, Y, Z $
are collinear (see Fano postulate).
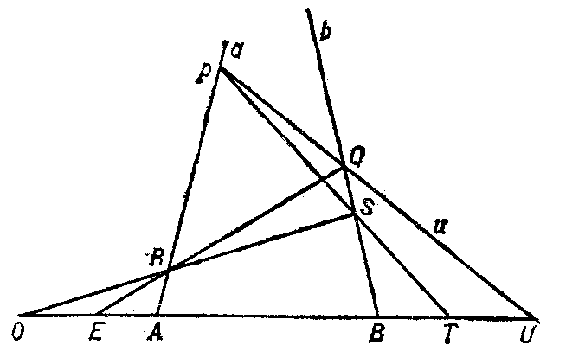
Figure: p075160b
Similar constructions can be carried out in a pencil of straight lines passing through a point, using a complete quadrilateral, a figure dual to a quadrangle, and leading to a skew-field $ K ^ {*} $
anti-isomorphic to $ K $.
The properties of the projective line $ l $
as an algebraic system are determined by the geometric (projectively-invariant) properties of the projective plane in which $ l $
lies. E.g., commutativity of $ K $
is equivalent to the Pappus axiom being true; Fano's postulate is equivalent to the characteristic of $ K $
being different from 2; if $ K $
has no other automorphisms but inner ones, then every projective transformation is a collineation, etc.
Using the skew-field $ K $
on the straight line, and hence in the projective space containing the line, one can introduce projective coordinates, giving an algebraic model of the projective space, so that the contents of the projective geometry is, in essence, determined by properties of the same skew-field $ K $
over which it is constructed.
In the wide sense, in projective geometry one studies the set of subspaces of projective space, which is a complemented modular lattice. Here one does not require the space to be finite-dimensional, but imposes the condition of completeness, existence of a homogeneous basis, etc. Accordingly, one can establish various connections with the theory of prime and regular rings, the theory of Abelian operator groups and other branches of algebra.
References
A collineation is a linear transformation of the homogeneous coordinates (Baer's terminology, [a2]).
The construction of projective geometry using the properties of its skew-field is rather old; it is essentially due to D. Hilbert [a1]. A modern approach was given by E. Artin [2].
References

