|
|
| (3 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
| | + | |
| | + | Out of 202 formulas, 199 were replaced by TEX code.--> |
| | + | |
| | + | {{TEX|semi-auto}}{{TEX|part}} |
| | Fourier and related algebras occur naturally in the [[Harmonic analysis|harmonic analysis]] of locally compact groups (cf. also [[Harmonic analysis, abstract|Harmonic analysis, abstract]]). They play an important role in the duality theories of these groups. | | Fourier and related algebras occur naturally in the [[Harmonic analysis|harmonic analysis]] of locally compact groups (cf. also [[Harmonic analysis, abstract|Harmonic analysis, abstract]]). They play an important role in the duality theories of these groups. |
| | | | |
| | ==Fourier–Stieltjes algebra.== | | ==Fourier–Stieltjes algebra.== |
| − | The Fourier–Stieltjes algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200801.png" /> and the Fourier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200802.png" /> of a locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200803.png" /> were introduced by P. Eymard in 1964 in [[#References|[a2]]] as respective replacements, in the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200804.png" /> is not Abelian, of the measure algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200805.png" /> of finite measures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200806.png" /> and of the convolution algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200807.png" /> of integrable functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200808.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f1200809.png" /> is the character group of the Abelian group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008010.png" /> (cf. also [[Character of a group|Character of a group]]). Indeed, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008011.png" /> is a locally compact Abelian group, the Fourier–Stieltjes transform of a finite measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008012.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008013.png" /> is the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008014.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008015.png" /> defined by | + | The Fourier–Stieltjes algebra $B ( G )$ and the Fourier algebra $A ( G )$ of a locally compact group $G$ were introduced by P. Eymard in 1964 in [[#References|[a2]]] as respective replacements, in the case when $G$ is not Abelian, of the measure algebra $M ( \hat { G } )$ of finite measures on $\hat { C }$ and of the convolution algebra $L _ { 1 } ( \hat { G } )$ of integrable functions on $\hat { C }$, where $\hat { C }$ is the character group of the Abelian group $G$ (cf. also [[Character of a group|Character of a group]]). Indeed, if $G$ is a locally compact Abelian group, the Fourier–Stieltjes transform of a finite measure $\mu$ on $\hat { C }$ is the function $\hat{\mu}$ on $G$ defined by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008016.png" /></td> </tr></table>
| + | \begin{equation*} \hat { \mu } ( x ) = \int _ { \hat{G} } \overline { \chi ( x ) } d \mu ( \chi ) , x \in G, \end{equation*} |
| | | | |
| − | and the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008017.png" /> of these functions is an algebra under pointwise multiplication, which is isomorphic to the measure algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008018.png" /> (cf. also [[Algebra of measures|Algebra of measures]]). Restricted to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008019.png" />, viewed as a subspace of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008020.png" />, the Fourier–Stieltjes transform is the [[Fourier transform|Fourier transform]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008021.png" /> and its image is, by definition, the Fourier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008022.png" />. The generalized Bochner theorem states that a [[Measurable function|measurable function]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008023.png" /> is equal, almost everywhere, to the Fourier–Stieltjes transform of a non-negative finite measure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008024.png" /> if and only if it is positive definite. Thus, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008025.png" /> can be defined as the linear span of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008026.png" /> of continuous positive-definite functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008027.png" />. This definition is still valid when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008028.png" /> is not Abelian. | + | and the space $B ( G )$ of these functions is an algebra under [[pointwise multiplication]], which is isomorphic to the measure algebra $M ( \hat { G } )$ (cf. also [[Algebra of measures|Algebra of measures]]). Restricted to $L _ { 1 } ( \hat { G } )$, viewed as a subspace of $M ( \hat { G } )$, the Fourier–Stieltjes transform is the [[Fourier transform|Fourier transform]] on $L _ { 1 } ( \hat { G } )$ and its image is, by definition, the Fourier algebra $A ( G )$. The generalized Bochner theorem states that a [[Measurable function|measurable function]] on $G$ is equal, almost everywhere, to the Fourier–Stieltjes transform of a non-negative finite measure on $\hat { C }$ if and only if it is positive definite. Thus, $B ( G )$ can be defined as the linear span of the set $P ( G )$ of continuous positive-definite functions on $G$. This definition is still valid when $G$ is not Abelian. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008029.png" /> be a locally compact group. The elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008030.png" /> are exactly the matrix elements of the unitary representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008031.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008032.png" /> if and only if there exist a [[Unitary representation|unitary representation]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008033.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008034.png" /> in a [[Hilbert space|Hilbert space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008035.png" /> and vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008036.png" /> such that | + | Let $G$ be a locally compact group. The elements of $B ( G )$ are exactly the matrix elements of the unitary representations of $G$: $\varphi \in B ( G )$ if and only if there exist a [[Unitary representation|unitary representation]] $\pi$ of $G$ in a [[Hilbert space|Hilbert space]] $H$ and vectors $\xi , \eta \in H$ such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008037.png" /></td> </tr></table>
| + | \begin{equation*} \varphi ( g ) = ( \xi , \eta ) ( g ) : = ( \pi ( g ) \xi , \eta ). \end{equation*} |
| | | | |
| − | The elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008038.png" /> are the matrix elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008039.png" />. Because of the existence of the tensor product of unitary representations, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008040.png" /> is an algebra under pointwise multiplication. The norm defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008041.png" />, where the infimum runs over all the representations <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008042.png" />, makes it into a [[Banach algebra|Banach algebra]]. The Fourier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008043.png" /> can be defined as the norm closure of the set of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008044.png" /> with compact support. It consists exactly of the matrix elements of the [[Regular representation|regular representation]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008045.png" />; equivalently, its elements are the functions of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008046.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008047.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008048.png" />. It is a closed ideal in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008049.png" />. | + | The elements of $P ( G )$ are the matrix elements $( \xi , \xi )$. Because of the existence of the tensor product of unitary representations, $B ( G )$ is an algebra under pointwise multiplication. The norm defined as $\| \varphi \| = \operatorname { inf } \| \xi \| \| \eta \|$, where the infimum runs over all the representations $\varphi = ( \xi , \eta )$, makes it into a [[Banach algebra|Banach algebra]]. The Fourier algebra $A ( G )$ can be defined as the norm closure of the set of elements of $B ( G )$ with compact support. It consists exactly of the matrix elements of the [[Regular representation|regular representation]] on $L _ { 2 } ( G )$; equivalently, its elements are the functions of the form $\xi ^ { * } \widetilde { \eta }$, where $\xi , \eta \in L _ { 2 } ( G )$ and $\widetilde{\eta} ( x ) = \eta ( x ^ { - 1 } )$. It is a closed ideal in $B ( G )$. |
| | | | |
| − | The most visible role of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008050.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008051.png" /> with respect to duality is that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008052.png" /> is the dual of the [[C*-algebra|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008053.png" />-algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008054.png" /> of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008055.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008056.png" /> is the pre-dual of the [[Von Neumann algebra|von Neumann algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008057.png" /> of its regular representation. The pairing is given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008058.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008060.png" />. The comparison with a similar result for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008061.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008062.png" />, namely <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008063.png" /> is the dual of the Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008064.png" /> of continuous functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008065.png" /> vanishing at infinity and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008066.png" /> is the pre-dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008067.png" />, leads to the theory of Kac algebras and a generalized Pontryagin theorem (see below). Two complementary results suggest to view <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008068.png" /> as a dual object of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008069.png" />; namely, Eymard's theorem states that the [[Topological space|topological space]] underlying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008070.png" /> can be recovered as the spectrum of the Fourier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008071.png" /> and Walter's theorem states that a locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008072.png" /> is determined, up to topological isomorphism, by the normed algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008073.png" />, or by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008074.png" />; the second result should be compared with theorems of J.G. Wendel and of B.E. Johnson, which establish the same property for the normed algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008075.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008076.png" />, respectively; see [[#References|[a5]]] for a survey of these results. | + | The most visible role of $B ( G )$ and $A ( G )$ with respect to duality is that $B ( G )$ is the dual of the [[C*-algebra|$C ^ { * }$-algebra]] $C ^ { * } ( G )$ of the group $G$ and $A ( G )$ is the pre-dual of the [[Von Neumann algebra|von Neumann algebra]] $W ^ { * } ( G )$ of its regular representation. The pairing is given by $\langle \varphi , T \rangle = ( \pi ( T ) \xi , \eta )$, where $\varphi = ( \xi , \eta ) \in B ( G )$ and $T \in C ^ { * } ( G )$. The comparison with a similar result for $M ( G )$ and $L _ { 1 } ( G )$, namely $M ( G )$ is the dual of the Banach space $C _ { 0 } ( G )$ of continuous functions on $G$ vanishing at infinity and $L _ { 1 } ( G )$ is the pre-dual of $L _ { \infty } ( G )$, leads to the theory of Kac algebras and a generalized Pontryagin theorem (see below). Two complementary results suggest to view $A ( G )$ as a dual object of the group $G$; namely, Eymard's theorem states that the [[Topological space|topological space]] underlying $G$ can be recovered as the spectrum of the Fourier algebra $A ( G )$ and Walter's theorem states that a locally compact group $G$ is determined, up to topological isomorphism, by the normed algebra $A ( G )$, or by $B ( G )$; the second result should be compared with theorems of J.G. Wendel and of B.E. Johnson, which establish the same property for the normed algebras $L _ { 1 } ( G )$ and $M ( G )$, respectively; see [[#References|[a5]]] for a survey of these results. |
| | | | |
| | ==Multipliers.== | | ==Multipliers.== |
| − | The multipliers of the Fourier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008077.png" /> reflect interesting properties of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008078.png" /> (cf. also [[Multiplier theory|Multiplier theory]]). First, the unit <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008079.png" /> (i.e., the constant function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008080.png" />) belongs to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008081.png" /> if and only if the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008082.png" /> is compact. Leptin's theorem (see [[#References|[a3]]]) asserts that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008083.png" /> has a bounded approximate unit if and only if the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008084.png" /> is amenable. A multiplier of the Fourier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008085.png" /> is a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008086.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008087.png" /> such that the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008088.png" /> of multiplication by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008089.png" /> maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008090.png" /> into itself. These multipliers form a Banach algebra under pointwise multiplication and the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008091.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008092.png" />. The transposed operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008093.png" /> is a bounded linear mapping from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008094.png" /> into itself. One says that the multiplier <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008095.png" /> is completely bounded if the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008096.png" /> is completely bounded, meaning that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008097.png" /> is finite, where the supremum runs over all integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008098.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f12008099.png" /> is the identity operator from the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080100.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080101.png" /> of complex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080102.png" />-matrices into itself. For example, the matrix elements of uniformly bounded representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080103.png" /> are such multipliers. The completely bounded multipliers form also a Banach algebra under pointwise multiplication and the norm <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080104.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080105.png" />. There is an alternative description of completely bounded multipliers as Schur multipliers, initiated by M.G. Krein [[#References|[a1]]] (cf. also [[Schur multiplicator|Schur multiplicator]]) and related to the metric theory of Grothendieck's topological tensor products. Given a measure space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080106.png" />, a measurable function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080107.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080108.png" /> is called a Schur multiplier if pointwise, or Schur, multiplication of kernels by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080109.png" /> defines a bounded linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080110.png" /> from the space of bounded operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080111.png" /> into itself; its Schur norm is then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080112.png" />. The Schur multipliers form a Banach algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080113.png" /> under pointwise multiplication. According to the Bożekjko–Fendler theorem, a continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080114.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080115.png" /> is a completely bounded multiplier of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080116.png" /> if and only if the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080117.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080118.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080119.png" /> is a Schur multiplier; moreover, the Schur norm and the completely bounded norms are equal. The continuous right-invariant Schur multipliers on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080120.png" /> are called Herz–Schur multipliers; they form a subalgebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080121.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080122.png" />, which is isometrically isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080123.png" />. The following norm-decreasing inclusions hold: | + | The multipliers of the Fourier algebra $A ( G )$ reflect interesting properties of the group $G$ (cf. also [[Multiplier theory|Multiplier theory]]). First, the unit $1$ (i.e., the constant function $1$) belongs to $A ( G )$ if and only if the group $G$ is compact. Leptin's theorem (see [[#References|[a3]]]) asserts that $A ( G )$ has a bounded approximate unit if and only if the group $G$ is amenable. A multiplier of the Fourier algebra $A ( G )$ is a function $\varphi$ on $G$ such that the operator $M _ { \varphi }$ of multiplication by $\varphi$ maps $A ( G )$ into itself. These multipliers form a Banach algebra under pointwise multiplication and the norm $\| \varphi \|_{ MA(G)} = \| M_\varphi \|$, denoted by $M A ( G )$. The transposed operator $\square ^ { t } M _ { \varphi }$ is a bounded linear mapping from $W ^ { * } ( G )$ into itself. One says that the multiplier $\varphi$ is completely bounded if the mapping $\square ^ { t } M _ { \varphi }$ is completely bounded, meaning that $\| \square ^ { t } M _ { \varphi } \| _ { \text{cb} } : = \operatorname { sup } \| \square ^ { t } M _ { \varphi } \otimes 1 _ { n } \|$ is finite, where the supremum runs over all integers $n \geq 1$ and $1_n$ is the identity operator from the $C ^ { * }$-algebra $M _ { n } ( \mathbf C )$ of complex $( n \times n )$-matrices into itself. For example, the matrix elements of uniformly bounded representations of $G$ are such multipliers. The completely bounded multipliers form also a Banach algebra under pointwise multiplication and the norm $\| \varphi \| _ {M_{0} A(G)} = \| M\|_{cb}$, denoted by $M _ { 0 } A ( G )$. There is an alternative description of completely bounded multipliers as Schur multipliers, initiated by M.G. Krein [[#References|[a1]]] (cf. also [[Schur multiplicator|Schur multiplicator]]) and related to the metric theory of Grothendieck's topological tensor products. Given a measure space $X$, a measurable function $\varphi$ on $X \times X$ is called a Schur multiplier if pointwise, or Schur, multiplication of kernels by $\varphi$ defines a bounded linear mapping $M _ { \varphi }$ from the space of bounded operators on $L _ { 2 } ( X )$ into itself; its Schur norm is then $\| \varphi \| _ { \text{S} } : = \| M_{ \varphi }\|$. The Schur multipliers form a Banach algebra $B ( X , X )$ under pointwise multiplication. According to the Bożekjko–Fendler theorem, a continuous function $\varphi$ on $G$ is a completely bounded multiplier of $A ( G )$ if and only if the function $\Gamma \varphi$ on $G \times G$ defined by $\Gamma \varphi ( x , y ) = \varphi ( x y ^ { - 1 } )$ is a Schur multiplier; moreover, the Schur norm and the completely bounded norms are equal. The continuous right-invariant Schur multipliers on $G \times G$ are called Herz–Schur multipliers; they form a subalgebra of $B ( G , G )$, denoted by $B _ { 2 } ( G )$, which is isometrically isomorphic to $M _ { 0 } A ( G )$. The following norm-decreasing inclusions hold: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080124.png" /></td> </tr></table>
| + | \begin{equation*} B ( G ) \subset M _ { 0 } A ( G ) \subset M A ( G ). \end{equation*} |
| | | | |
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080125.png" /> is amenable, these inclusions are equalities; on the other hand, according to Losert's theorem, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080126.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080127.png" /> is amenable; the equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080128.png" /> gives the same conclusion, at least when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080129.png" /> is discrete (M. Bożekjko and J. Wysoczanski). A locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080130.png" /> is called weakly amenable if there exists an approximate unit in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080131.png" /> which is bounded in the norm of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080132.png" />. The Haagerup constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080133.png" /> is defined as the infimum of these bounds over all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080134.png" />-bounded approximate units. Free groups and, more generally simple Lie groups with finite centre and real rank one and their lattices, are weakly amenable and their Haagerup constants have been computed in [[#References|[a4]]]. For example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080135.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080136.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080137.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080138.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080139.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080140.png" />). Groups of real rank greater than one are not weakly amenable. See also [[#References|[a4]]] for references to completely bounded multipliers. | + | When $G$ is amenable, these inclusions are equalities; on the other hand, according to Losert's theorem, if $B ( G ) = M A ( G )$, then $G$ is amenable; the equality $B ( G ) = M _ { 0 } A ( G )$ gives the same conclusion, at least when $G$ is discrete (M. Bożekjko and J. Wysoczanski). A locally compact group $G$ is called weakly amenable if there exists an approximate unit in $A ( G )$ which is bounded in the norm of $M _ { 0 } A ( G )$. The Haagerup constant $\Lambda _ { G }$ is defined as the infimum of these bounds over all $M _ { 0 } A ( G )$-bounded approximate units. Free groups and, more generally simple Lie groups with finite centre and real rank one and their lattices, are weakly amenable and their Haagerup constants have been computed in [[#References|[a4]]]. For example, $\Lambda _ { G } = 1$ for $G = SO ( 1 , n )$ or $F _ { n }$ and $\Lambda _ { G } = 2 n - 1$ for $G = \operatorname { Sp } ( 1 , n )$ ($n \geq 2$). Groups of real rank greater than one are not weakly amenable. See also [[#References|[a4]]] for references to completely bounded multipliers. |
| | | | |
| − | ==<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080141.png" />-Fourier algebras.== | + | ==$L _ { p }$-Fourier algebras.== |
| − | An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080142.png" />-version of the Fourier algebra has been developed for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080143.png" /> (see [[#References|[a3]]] for a detailed account and references). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080144.png" /> be given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080145.png" />. The Herz–Figa–Talamanca algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080146.png" /> is the space of functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080147.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080148.png" /> of the form | + | An $L _ { p }$-version of the Fourier algebra has been developed for $1 < p < \infty$ (see [[#References|[a3]]] for a detailed account and references). Let $q$ be given by $1 / p + 1 / q = 1$. The Herz–Figa–Talamanca algebra $A _ { p } ( G )$ is the space of functions $\varphi$ on $G$ of the form |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080149.png" /></td> </tr></table>
| + | \begin{equation*} \varphi = \sum _ { k = 1 } ^ { \infty } f _ { k } * \widetilde{g} _ { k }, \end{equation*} |
| | | | |
| | where | | where |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080150.png" /></td> </tr></table>
| + | \begin{equation*} f _ { k } \in L _ { p } ( G ) , g _ { k } \in L _ { q } ( G ) , \sum _ { k = 1 } ^ { \infty } \| f _ { k } \| \| g _ { k } \| < \infty, \end{equation*} |
| | | | |
| − | with pointwise multiplication. It is the quotient of the projective tensor product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080151.png" /> with respect to the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080152.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080153.png" />. Again, the amenability of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080154.png" /> is equivalent to the existence of a bounded approximate unit in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080155.png" />. Just as above, one defines for a measure space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080156.png" /> the Schur multiplier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080157.png" /> as the space of functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080158.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080159.png" /> such that the Schur multiplication <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080160.png" /> sends the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080161.png" /> of bounded operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080162.png" /> (or, equivalently, its pre-dual <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080163.png" />) into itself, and the Herz–Schur multiplier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080164.png" /> as the space of continuous functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080165.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080166.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080167.png" /> belongs to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080168.png" />; the product is pointwise multiplication. Since the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080169.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080170.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080171.png" /> intertwines <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080172.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080173.png" />, a Herz–Schur multiplier <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080174.png" /> is a multiplier of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080175.png" /> and the inclusion <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080176.png" /> decreases the norm. It is an equality if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080177.png" /> is amenable. These algebras are also related to convolution operators. In particular, the dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080178.png" /> is the weak closure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080179.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080180.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080181.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080182.png" /> acts by left convolution. Banach algebra properties of the Fourier algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080183.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080184.png" /> have been much studied; see [[#References|[a3]]] for a bibliography up to 1984. | + | with pointwise multiplication. It is the quotient of the projective tensor product $L _ { p } ( G ) \otimes \widehat{} L _ { q } ( G )$ with respect to the mapping $P$ defined by $P ( f \otimes g ) = f * g$. Again, the amenability of $G$ is equivalent to the existence of a bounded approximate unit in $A _ { p } ( G )$. Just as above, one defines for a measure space $X$ the Schur multiplier algebra $B _ { p } ( X , X )$ as the space of functions $\varphi$ on $X \times X$ such that the Schur multiplication $M _ { \varphi }$ sends the space $\mathcal{L} ( L _ { q } ( X ) )$ of bounded operators on $L _ { q } ( X )$ (or, equivalently, its pre-dual $L _ { p } ( G ) \otimes \widehat{} L _ { q } ( G )$) into itself, and the Herz–Schur multiplier algebra $B _ { p } ( G )$ as the space of continuous functions $\varphi$ on $G$ such that $\Gamma \varphi$ belongs to $B _ { p } ( G , G )$; the product is pointwise multiplication. Since the mapping $P$ from $L _ { p } ( G ) \otimes \widehat{} L _ { q } ( G )$ onto $A _ { p } ( G )$ intertwines $M _ { \varphi }$ and $M_ { \Gamma \varphi}$, a Herz–Schur multiplier $\varphi \in B _ { p } ( G )$ is a multiplier of $A _ { p } ( G )$ and the inclusion $B _ { p } ( G ) \subset M A _ { p } ( G )$ decreases the norm. It is an equality if $G$ is amenable. These algebras are also related to convolution operators. In particular, the dual of $A _ { p } ( G )$ is the weak closure $P M _ { q } ( G )$ of $L _ { 1 } ( G )$ in $\mathcal{L} ( L _ { q } ( X ) )$, where $L _ { 1 } ( G )$ acts by left convolution. Banach algebra properties of the Fourier algebras $A ( G )$ and $A _ { p } ( G )$ have been much studied; see [[#References|[a3]]] for a bibliography up to 1984. |
| | | | |
| | ==Kac algebras.== | | ==Kac algebras.== |
| − | Fourier algebras are natural objects in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080185.png" />-algebraic theory of [[Quantum groups|quantum groups]] and groupoids. In particular, Kac algebras (see [[#References|[a5]]]) provide a symmetric framework for duality, which extends the classical [[Pontryagin duality|Pontryagin duality]] theory for locally compact Abelian groups. Each Kac algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080186.png" /> has a dual Kac algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080187.png" /> and the dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080188.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080189.png" />. The Fourier algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080190.png" /> is the pre-dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080191.png" /> and the Fourier–Stieltjes algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080192.png" /> is the dual of the enveloping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080193.png" />-algebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080194.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080195.png" /> is the Kac algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080196.png" /> of a locally compact group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080197.png" />, then the dual Kac algebra is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080198.png" /> and the corresponding Fourier and Fourier–Stieltjes algebras are: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080199.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080200.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080201.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080202.png" />. | + | Fourier algebras are natural objects in the $C ^ { * }$-algebraic theory of [[Quantum groups|quantum groups]] and groupoids. In particular, Kac algebras (see [[#References|[a5]]]) provide a symmetric framework for duality, which extends the classical [[Pontryagin duality|Pontryagin duality]] theory for locally compact Abelian groups. Each Kac algebra $K$ has a dual Kac algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080187.png"/> and the dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080188.png"/> is isomorphic to $K$. The Fourier algebra $A ( K ) \subset K$ is the pre-dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f120/f120080/f120080191.png"/> and the Fourier–Stieltjes algebra $B ( K )$ is the dual of the enveloping $C ^ { * }$-algebra of $A ( \widehat{K} )$. If $K$ is the Kac algebra $L _ { \infty } ( G )$ of a locally compact group $G$, then the dual Kac algebra is $\hat { K } = W ^ { * } ( G )$ and the corresponding Fourier and Fourier–Stieltjes algebras are: $A ( K ) = A ( G )$, $B ( K ) = B ( G )$, $A ( \hat { K } ) = L _ { 1 } ( G )$ and $B ( \hat { K } ) = M ( G )$. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Krein, "Hermitian-positive kernels on homogeneous spaces I–II" ''Amer. Math. Soc. Transl. (2)'' , '''34''' (1963) pp. 69–164 ''Ukrain. Mat. Z.'' , '''1–2''' (1949/50) pp. 64–98; 10–59</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Eymard, "L'algèbre de Fourier d'un groupe localement compact" ''Bull. Soc. Math. France'' , '''92''' (1964) pp. 181–236</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.-P. Pier, "Amenable locally compact groups" , Wiley–Interscience (1984)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Cowling, U. Haagerup, "Completely bounded multipliers of the Fourier algebra of a simple Lie groups of real rank one" ''Invent. Math.'' , '''96''' : 3 (1989) pp. 507–549</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Enock, J.-M. Schwartz, "Kac algebras and duality of locally compact groups" , Springer (1992)</TD></TR></table> | + | <table> |
| | + | <tr><td valign="top">[a1]</td> <td valign="top"> M. Krein, "Hermitian-positive kernels on homogeneous spaces I–II" ''Amer. Math. Soc. Transl. (2)'' , '''34''' (1963) pp. 69–164 ''Ukrain. Mat. Z.'' , '''1–2''' (1949/50) pp. 64–98; 10–59</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> P. Eymard, "L'algèbre de Fourier d'un groupe localement compact" ''Bull. Soc. Math. France'' , '''92''' (1964) pp. 181–236</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J.-P. Pier, "Amenable locally compact groups" , Wiley–Interscience (1984)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> M. Cowling, U. Haagerup, "Completely bounded multipliers of the Fourier algebra of a simple Lie groups of real rank one" ''Invent. Math.'' , '''96''' : 3 (1989) pp. 507–549</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> M. Enock, J.-M. Schwartz, "Kac algebras and duality of locally compact groups" , Springer (1992)</td></tr> |
| | + | </table> |
Fourier and related algebras occur naturally in the harmonic analysis of locally compact groups (cf. also Harmonic analysis, abstract). They play an important role in the duality theories of these groups.
Fourier–Stieltjes algebra.
The Fourier–Stieltjes algebra $B ( G )$ and the Fourier algebra $A ( G )$ of a locally compact group $G$ were introduced by P. Eymard in 1964 in [a2] as respective replacements, in the case when $G$ is not Abelian, of the measure algebra $M ( \hat { G } )$ of finite measures on $\hat { C }$ and of the convolution algebra $L _ { 1 } ( \hat { G } )$ of integrable functions on $\hat { C }$, where $\hat { C }$ is the character group of the Abelian group $G$ (cf. also Character of a group). Indeed, if $G$ is a locally compact Abelian group, the Fourier–Stieltjes transform of a finite measure $\mu$ on $\hat { C }$ is the function $\hat{\mu}$ on $G$ defined by
\begin{equation*} \hat { \mu } ( x ) = \int _ { \hat{G} } \overline { \chi ( x ) } d \mu ( \chi ) , x \in G, \end{equation*}
and the space $B ( G )$ of these functions is an algebra under pointwise multiplication, which is isomorphic to the measure algebra $M ( \hat { G } )$ (cf. also Algebra of measures). Restricted to $L _ { 1 } ( \hat { G } )$, viewed as a subspace of $M ( \hat { G } )$, the Fourier–Stieltjes transform is the Fourier transform on $L _ { 1 } ( \hat { G } )$ and its image is, by definition, the Fourier algebra $A ( G )$. The generalized Bochner theorem states that a measurable function on $G$ is equal, almost everywhere, to the Fourier–Stieltjes transform of a non-negative finite measure on $\hat { C }$ if and only if it is positive definite. Thus, $B ( G )$ can be defined as the linear span of the set $P ( G )$ of continuous positive-definite functions on $G$. This definition is still valid when $G$ is not Abelian.
Let $G$ be a locally compact group. The elements of $B ( G )$ are exactly the matrix elements of the unitary representations of $G$: $\varphi \in B ( G )$ if and only if there exist a unitary representation $\pi$ of $G$ in a Hilbert space $H$ and vectors $\xi , \eta \in H$ such that
\begin{equation*} \varphi ( g ) = ( \xi , \eta ) ( g ) : = ( \pi ( g ) \xi , \eta ). \end{equation*}
The elements of $P ( G )$ are the matrix elements $( \xi , \xi )$. Because of the existence of the tensor product of unitary representations, $B ( G )$ is an algebra under pointwise multiplication. The norm defined as $\| \varphi \| = \operatorname { inf } \| \xi \| \| \eta \|$, where the infimum runs over all the representations $\varphi = ( \xi , \eta )$, makes it into a Banach algebra. The Fourier algebra $A ( G )$ can be defined as the norm closure of the set of elements of $B ( G )$ with compact support. It consists exactly of the matrix elements of the regular representation on $L _ { 2 } ( G )$; equivalently, its elements are the functions of the form $\xi ^ { * } \widetilde { \eta }$, where $\xi , \eta \in L _ { 2 } ( G )$ and $\widetilde{\eta} ( x ) = \eta ( x ^ { - 1 } )$. It is a closed ideal in $B ( G )$.
The most visible role of $B ( G )$ and $A ( G )$ with respect to duality is that $B ( G )$ is the dual of the $C ^ { * }$-algebra $C ^ { * } ( G )$ of the group $G$ and $A ( G )$ is the pre-dual of the von Neumann algebra $W ^ { * } ( G )$ of its regular representation. The pairing is given by $\langle \varphi , T \rangle = ( \pi ( T ) \xi , \eta )$, where $\varphi = ( \xi , \eta ) \in B ( G )$ and $T \in C ^ { * } ( G )$. The comparison with a similar result for $M ( G )$ and $L _ { 1 } ( G )$, namely $M ( G )$ is the dual of the Banach space $C _ { 0 } ( G )$ of continuous functions on $G$ vanishing at infinity and $L _ { 1 } ( G )$ is the pre-dual of $L _ { \infty } ( G )$, leads to the theory of Kac algebras and a generalized Pontryagin theorem (see below). Two complementary results suggest to view $A ( G )$ as a dual object of the group $G$; namely, Eymard's theorem states that the topological space underlying $G$ can be recovered as the spectrum of the Fourier algebra $A ( G )$ and Walter's theorem states that a locally compact group $G$ is determined, up to topological isomorphism, by the normed algebra $A ( G )$, or by $B ( G )$; the second result should be compared with theorems of J.G. Wendel and of B.E. Johnson, which establish the same property for the normed algebras $L _ { 1 } ( G )$ and $M ( G )$, respectively; see [a5] for a survey of these results.
Multipliers.
The multipliers of the Fourier algebra $A ( G )$ reflect interesting properties of the group $G$ (cf. also Multiplier theory). First, the unit $1$ (i.e., the constant function $1$) belongs to $A ( G )$ if and only if the group $G$ is compact. Leptin's theorem (see [a3]) asserts that $A ( G )$ has a bounded approximate unit if and only if the group $G$ is amenable. A multiplier of the Fourier algebra $A ( G )$ is a function $\varphi$ on $G$ such that the operator $M _ { \varphi }$ of multiplication by $\varphi$ maps $A ( G )$ into itself. These multipliers form a Banach algebra under pointwise multiplication and the norm $\| \varphi \|_{ MA(G)} = \| M_\varphi \|$, denoted by $M A ( G )$. The transposed operator $\square ^ { t } M _ { \varphi }$ is a bounded linear mapping from $W ^ { * } ( G )$ into itself. One says that the multiplier $\varphi$ is completely bounded if the mapping $\square ^ { t } M _ { \varphi }$ is completely bounded, meaning that $\| \square ^ { t } M _ { \varphi } \| _ { \text{cb} } : = \operatorname { sup } \| \square ^ { t } M _ { \varphi } \otimes 1 _ { n } \|$ is finite, where the supremum runs over all integers $n \geq 1$ and $1_n$ is the identity operator from the $C ^ { * }$-algebra $M _ { n } ( \mathbf C )$ of complex $( n \times n )$-matrices into itself. For example, the matrix elements of uniformly bounded representations of $G$ are such multipliers. The completely bounded multipliers form also a Banach algebra under pointwise multiplication and the norm $\| \varphi \| _ {M_{0} A(G)} = \| M\|_{cb}$, denoted by $M _ { 0 } A ( G )$. There is an alternative description of completely bounded multipliers as Schur multipliers, initiated by M.G. Krein [a1] (cf. also Schur multiplicator) and related to the metric theory of Grothendieck's topological tensor products. Given a measure space $X$, a measurable function $\varphi$ on $X \times X$ is called a Schur multiplier if pointwise, or Schur, multiplication of kernels by $\varphi$ defines a bounded linear mapping $M _ { \varphi }$ from the space of bounded operators on $L _ { 2 } ( X )$ into itself; its Schur norm is then $\| \varphi \| _ { \text{S} } : = \| M_{ \varphi }\|$. The Schur multipliers form a Banach algebra $B ( X , X )$ under pointwise multiplication. According to the Bożekjko–Fendler theorem, a continuous function $\varphi$ on $G$ is a completely bounded multiplier of $A ( G )$ if and only if the function $\Gamma \varphi$ on $G \times G$ defined by $\Gamma \varphi ( x , y ) = \varphi ( x y ^ { - 1 } )$ is a Schur multiplier; moreover, the Schur norm and the completely bounded norms are equal. The continuous right-invariant Schur multipliers on $G \times G$ are called Herz–Schur multipliers; they form a subalgebra of $B ( G , G )$, denoted by $B _ { 2 } ( G )$, which is isometrically isomorphic to $M _ { 0 } A ( G )$. The following norm-decreasing inclusions hold:
\begin{equation*} B ( G ) \subset M _ { 0 } A ( G ) \subset M A ( G ). \end{equation*}
When $G$ is amenable, these inclusions are equalities; on the other hand, according to Losert's theorem, if $B ( G ) = M A ( G )$, then $G$ is amenable; the equality $B ( G ) = M _ { 0 } A ( G )$ gives the same conclusion, at least when $G$ is discrete (M. Bożekjko and J. Wysoczanski). A locally compact group $G$ is called weakly amenable if there exists an approximate unit in $A ( G )$ which is bounded in the norm of $M _ { 0 } A ( G )$. The Haagerup constant $\Lambda _ { G }$ is defined as the infimum of these bounds over all $M _ { 0 } A ( G )$-bounded approximate units. Free groups and, more generally simple Lie groups with finite centre and real rank one and their lattices, are weakly amenable and their Haagerup constants have been computed in [a4]. For example, $\Lambda _ { G } = 1$ for $G = SO ( 1 , n )$ or $F _ { n }$ and $\Lambda _ { G } = 2 n - 1$ for $G = \operatorname { Sp } ( 1 , n )$ ($n \geq 2$). Groups of real rank greater than one are not weakly amenable. See also [a4] for references to completely bounded multipliers.
$L _ { p }$-Fourier algebras.
An $L _ { p }$-version of the Fourier algebra has been developed for $1 < p < \infty$ (see [a3] for a detailed account and references). Let $q$ be given by $1 / p + 1 / q = 1$. The Herz–Figa–Talamanca algebra $A _ { p } ( G )$ is the space of functions $\varphi$ on $G$ of the form
\begin{equation*} \varphi = \sum _ { k = 1 } ^ { \infty } f _ { k } * \widetilde{g} _ { k }, \end{equation*}
where
\begin{equation*} f _ { k } \in L _ { p } ( G ) , g _ { k } \in L _ { q } ( G ) , \sum _ { k = 1 } ^ { \infty } \| f _ { k } \| \| g _ { k } \| < \infty, \end{equation*}
with pointwise multiplication. It is the quotient of the projective tensor product $L _ { p } ( G ) \otimes \widehat{} L _ { q } ( G )$ with respect to the mapping $P$ defined by $P ( f \otimes g ) = f * g$. Again, the amenability of $G$ is equivalent to the existence of a bounded approximate unit in $A _ { p } ( G )$. Just as above, one defines for a measure space $X$ the Schur multiplier algebra $B _ { p } ( X , X )$ as the space of functions $\varphi$ on $X \times X$ such that the Schur multiplication $M _ { \varphi }$ sends the space $\mathcal{L} ( L _ { q } ( X ) )$ of bounded operators on $L _ { q } ( X )$ (or, equivalently, its pre-dual $L _ { p } ( G ) \otimes \widehat{} L _ { q } ( G )$) into itself, and the Herz–Schur multiplier algebra $B _ { p } ( G )$ as the space of continuous functions $\varphi$ on $G$ such that $\Gamma \varphi$ belongs to $B _ { p } ( G , G )$; the product is pointwise multiplication. Since the mapping $P$ from $L _ { p } ( G ) \otimes \widehat{} L _ { q } ( G )$ onto $A _ { p } ( G )$ intertwines $M _ { \varphi }$ and $M_ { \Gamma \varphi}$, a Herz–Schur multiplier $\varphi \in B _ { p } ( G )$ is a multiplier of $A _ { p } ( G )$ and the inclusion $B _ { p } ( G ) \subset M A _ { p } ( G )$ decreases the norm. It is an equality if $G$ is amenable. These algebras are also related to convolution operators. In particular, the dual of $A _ { p } ( G )$ is the weak closure $P M _ { q } ( G )$ of $L _ { 1 } ( G )$ in $\mathcal{L} ( L _ { q } ( X ) )$, where $L _ { 1 } ( G )$ acts by left convolution. Banach algebra properties of the Fourier algebras $A ( G )$ and $A _ { p } ( G )$ have been much studied; see [a3] for a bibliography up to 1984.
Kac algebras.
Fourier algebras are natural objects in the $C ^ { * }$-algebraic theory of quantum groups and groupoids. In particular, Kac algebras (see [a5]) provide a symmetric framework for duality, which extends the classical Pontryagin duality theory for locally compact Abelian groups. Each Kac algebra $K$ has a dual Kac algebra 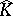 and the dual of
and the dual of 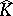 is isomorphic to $K$. The Fourier algebra $A ( K ) \subset K$ is the pre-dual of
is isomorphic to $K$. The Fourier algebra $A ( K ) \subset K$ is the pre-dual of 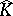 and the Fourier–Stieltjes algebra $B ( K )$ is the dual of the enveloping $C ^ { * }$-algebra of $A ( \widehat{K} )$. If $K$ is the Kac algebra $L _ { \infty } ( G )$ of a locally compact group $G$, then the dual Kac algebra is $\hat { K } = W ^ { * } ( G )$ and the corresponding Fourier and Fourier–Stieltjes algebras are: $A ( K ) = A ( G )$, $B ( K ) = B ( G )$, $A ( \hat { K } ) = L _ { 1 } ( G )$ and $B ( \hat { K } ) = M ( G )$.
and the Fourier–Stieltjes algebra $B ( K )$ is the dual of the enveloping $C ^ { * }$-algebra of $A ( \widehat{K} )$. If $K$ is the Kac algebra $L _ { \infty } ( G )$ of a locally compact group $G$, then the dual Kac algebra is $\hat { K } = W ^ { * } ( G )$ and the corresponding Fourier and Fourier–Stieltjes algebras are: $A ( K ) = A ( G )$, $B ( K ) = B ( G )$, $A ( \hat { K } ) = L _ { 1 } ( G )$ and $B ( \hat { K } ) = M ( G )$.
References
| [a1] | M. Krein, "Hermitian-positive kernels on homogeneous spaces I–II" Amer. Math. Soc. Transl. (2) , 34 (1963) pp. 69–164 Ukrain. Mat. Z. , 1–2 (1949/50) pp. 64–98; 10–59 |
| [a2] | P. Eymard, "L'algèbre de Fourier d'un groupe localement compact" Bull. Soc. Math. France , 92 (1964) pp. 181–236 |
| [a3] | J.-P. Pier, "Amenable locally compact groups" , Wiley–Interscience (1984) |
| [a4] | M. Cowling, U. Haagerup, "Completely bounded multipliers of the Fourier algebra of a simple Lie groups of real rank one" Invent. Math. , 96 : 3 (1989) pp. 507–549 |
| [a5] | M. Enock, J.-M. Schwartz, "Kac algebras and duality of locally compact groups" , Springer (1992) |
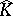 and the dual of
and the dual of 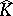 is isomorphic to $K$. The Fourier algebra $A ( K ) \subset K$ is the pre-dual of
is isomorphic to $K$. The Fourier algebra $A ( K ) \subset K$ is the pre-dual of 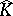 and the Fourier–Stieltjes algebra $B ( K )$ is the dual of the enveloping $C ^ { * }$-algebra of $A ( \widehat{K} )$. If $K$ is the Kac algebra $L _ { \infty } ( G )$ of a locally compact group $G$, then the dual Kac algebra is $\hat { K } = W ^ { * } ( G )$ and the corresponding Fourier and Fourier–Stieltjes algebras are: $A ( K ) = A ( G )$, $B ( K ) = B ( G )$, $A ( \hat { K } ) = L _ { 1 } ( G )$ and $B ( \hat { K } ) = M ( G )$.
and the Fourier–Stieltjes algebra $B ( K )$ is the dual of the enveloping $C ^ { * }$-algebra of $A ( \widehat{K} )$. If $K$ is the Kac algebra $L _ { \infty } ( G )$ of a locally compact group $G$, then the dual Kac algebra is $\hat { K } = W ^ { * } ( G )$ and the corresponding Fourier and Fourier–Stieltjes algebras are: $A ( K ) = A ( G )$, $B ( K ) = B ( G )$, $A ( \hat { K } ) = L _ { 1 } ( G )$ and $B ( \hat { K } ) = M ( G )$.