|
|
| (3 intermediate revisions by 2 users not shown) |
| Line 1: |
Line 1: |
| | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
| | + | |
| | + | Out of 197 formulas, 196 were replaced by TEX code.--> |
| | + | |
| | + | {{TEX|semi-auto}}{{TEX|part}} |
| | ''convexity in complex analysis'' | | ''convexity in complex analysis'' |
| | | | |
| − | A domain or compact subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c1200102.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c1200103.png" /> is said to be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c1200105.png" />-convex if for any complex line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c1200106.png" /> the intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c1200107.png" /> is both connected and simply connected (meaning that its complement in the [[Riemann sphere|Riemann sphere]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c1200108.png" /> is connected; cf. also [[Connected set|Connected set]]; [[Simply-connected domain|Simply-connected domain]]). The notion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c1200109.png" />-convexity is an intermediate one, in the sense that any geometrically [[Convex set|convex set]] is necessarily <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001010.png" />-convex, whereas <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001011.png" />-convexity implies holomorphic convexity (or pseudo-convexity; cf. also [[Pseudo-convex and pseudo-concave|Pseudo-convex and pseudo-concave]]). In particular, a real subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001012.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001013.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001015.png" />-convex if and only if it is convex in the ordinary, geometrical, sense. Open or compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001016.png" />-convex subsets are in several respects the natural sets when it comes to studying properties of holomorphic functions that are invariant under affine (or projective) transformations. They often play a role analogous to that of convex sets in real analysis. | + | A domain or compact subset $E$ in $\mathbf{C} ^ { n }$ is said to be $\mathbf{C}$-convex if for any complex line $\operatorname{l} \subset \mathbf{C} ^ { n }$ the intersection $E \cap \bf l$ is both connected and simply connected (meaning that its complement in the [[Riemann sphere|Riemann sphere]] $\text{l} \cup \{ \infty \}$ is connected; cf. also [[Connected set|Connected set]]; [[Simply-connected domain|Simply-connected domain]]). The notion of $\mathbf{C}$-convexity is an intermediate one, in the sense that any geometrically [[Convex set|convex set]] is necessarily $\mathbf{C}$-convex, whereas $\mathbf{C}$-convexity implies holomorphic convexity (or pseudo-convexity; cf. also [[Pseudo-convex and pseudo-concave|Pseudo-convex and pseudo-concave]]). In particular, a real subset $E$ in $\mathbf{R} ^ { n } \subset \mathbf{C} ^ { n }$ is $\mathbf{C}$-convex if and only if it is convex in the ordinary, geometrical, sense. Open or compact $\mathbf{C}$-convex subsets are in several respects the natural sets when it comes to studying properties of holomorphic functions that are invariant under affine (or projective) transformations. They often play a role analogous to that of convex sets in real analysis. |
| | | | |
| − | ==Topology of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001017.png" />-convex sets.== | + | ==Topology of $\mathbf{C}$-convex sets.== |
| − | Any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001018.png" />-convex domain is homeomorphically equivalent to the open unit ball <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001019.png" />, and a compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001020.png" />-convex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001021.png" /> is also topologically simple in the sense that it has vanishing reduced [[Cohomology|cohomology]]: | + | Any $\mathbf{C}$-convex domain is homeomorphically equivalent to the open unit ball $| z _ { 1 } | ^ { 2 } + \ldots + | z _ { n } | ^ { 2 } < 1$, and a compact $\mathbf{C}$-convex set $E$ is also topologically simple in the sense that it has vanishing reduced [[Cohomology|cohomology]]: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001022.png" /></td> </tr></table>
| + | \begin{equation*} H ^ { 0 } ( E ) = \mathbf{Z} , \quad H ^ { p } ( E ) = 0 , p > 0. \end{equation*} |
| | | | |
| − | The operations of forming the closure and the interior are not well-adapted to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001023.png" />-convexity. There exist, e.g., compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001024.png" />-convex sets with non-connected interior. Also, the intersection of two <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001025.png" />-convex sets is not necessarily <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001026.png" />-convex. | + | The operations of forming the closure and the interior are not well-adapted to $\mathbf{C}$-convexity. There exist, e.g., compact $\mathbf{C}$-convex sets with non-connected interior. Also, the intersection of two $\mathbf{C}$-convex sets is not necessarily $\mathbf{C}$-convex. |
| | | | |
| | ==Projective invariance.== | | ==Projective invariance.== |
| − | It is natural to consider a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001027.png" />-convex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001028.png" /> also as a subset of the complex projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001029.png" />. Each non-trivial complex linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001030.png" /> descends to a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001031.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001032.png" /> corresponds to the kernel of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001033.png" />. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001034.png" /> is then called a projective transformation, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001035.png" />-convexity is invariant under any such transformation: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001036.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001037.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001038.png" />-convex subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001039.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001040.png" />, respectively, then both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001041.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001042.png" /> are also <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001043.png" />-convex. | + | It is natural to consider a $\mathbf{C}$-convex set $E \subset \mathbf{C} ^ { n }$ also as a subset of the complex projective space $\mathbf{P} ^ { n } \supset \mathbf{C} ^ { n }$. Each non-trivial complex linear mapping $\tilde{T} : {\bf C} ^ { m + 1 } \rightarrow {\bf C} ^ { n + 1 }$ descends to a mapping $T : \mathbf{P} ^ { m } \backslash X \rightarrow \mathbf{P} ^ { n }$, where $X$ corresponds to the kernel of $\tilde{T}$. The mapping $T$ is then called a projective transformation, and $\mathbf{C}$-convexity is invariant under any such transformation: If $E$ and $F$ are $\mathbf{C}$-convex subsets of ${\bf P} ^ { m } \backslash X$ and $\mathbf{P} ^ { n }$, respectively, then both $T ( E )$ and $T ^ { - 1 } ( F )$ are also $\mathbf{C}$-convex. |
| | | | |
| − | A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001044.png" />-convex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001045.png" /> is said to be non-degenerate if it is not of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001047.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001048.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001050.png" /> is a projective transformation. Examples of degenerate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001052.png" />-convex sets are those that are contained in complex hyperplanes, or of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001053.png" />. It is an interesting fact that far from all one-dimensional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001054.png" />-convex sets can occur as the intersection of a multi-dimensional non-degenerate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001055.png" />-convex set with a complex line. | + | A $\mathbf{C}$-convex set $E \subset {\bf C} ^ { n } \subset {\bf P} ^ { n }$ is said to be non-degenerate if it is not of the form $T ( F )$ or $T ^ { - 1 } ( F )$, where $F \subset \mathbf{P} ^ { n - 1 }$ and $T$ is a projective transformation. Examples of degenerate $\mathbf{C}$-convex sets are those that are contained in complex hyperplanes, or of the form $E \times \mathbf C$. It is an interesting fact that far from all one-dimensional $\mathbf{C}$-convex sets can occur as the intersection of a multi-dimensional non-degenerate $\mathbf{C}$-convex set with a complex line. |
| | | | |
| | ==Dual complement and linear convexity.== | | ==Dual complement and linear convexity.== |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001056.png" /> is any subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001057.png" />, then its dual complement <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001058.png" /> is, by definition, the collection of all complex hyperplanes that do not intersect <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001059.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001060.png" /> this is just the usual complement of a set in the Riemann sphere, and in higher dimensions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001061.png" /> can be considered as a subset of the dual projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001062.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001063.png" /> is an open (or compact) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001064.png" />-convex set, then its dual complement <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001065.png" /> is a compact (respectively, open) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001066.png" />-convex set. Moreover, such a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001067.png" />-convex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001068.png" /> is also linearly convex in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001069.png" />, i.e. the complement of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001070.png" /> is a union of complex hyperplanes. There are, however, many linearly convex sets that are not <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001071.png" />-convex. For instance, any Cartesian product of subsets of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001072.png" /> is linearly convex, but it is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001073.png" />-convex only if each factor is convex in the usual sense. A connected component of a linearly convex set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001074.png" /> is not necessarily linearly convex. In fact, a compact or open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001075.png" /> which is equal to one or several connected components of its linearly convex hull <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001076.png" /> is said to be weakly linearly convex. For an open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001077.png" />, weak linear convexity amounts to the condition that through any boundary point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001078.png" /> there should pass a complex hyperplane not intersecting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001079.png" />, and this does not in general imply linear convexity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001080.png" />. Any weakly linearly convex open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001081.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001082.png" /> is pseudo-convex. | + | If $E$ is any subset of $\mathbf{C} ^ { n } \subset \mathbf{P} ^ { n }$, then its dual complement $E ^ { * }$ is, by definition, the collection of all complex hyperplanes that do not intersect $E$. When $n = 1$ this is just the usual complement of a set in the Riemann sphere, and in higher dimensions $E ^ { * }$ can be considered as a subset of the dual projective space ${\bf P}^ { n^* }$. If $E$ is an open (or compact) $\mathbf{C}$-convex set, then its dual complement $E ^ { * }$ is a compact (respectively, open) $\mathbf{C}$-convex set. Moreover, such a $\mathbf{C}$-convex set $E$ is also linearly convex in the sense that $E = E ^ { * * }$, i.e. the complement of $E$ is a union of complex hyperplanes. There are, however, many linearly convex sets that are not $\mathbf{C}$-convex. For instance, any Cartesian product of subsets of $\mathbf{C}$ is linearly convex, but it is $\mathbf{C}$-convex only if each factor is convex in the usual sense. A connected component of a linearly convex set $E$ is not necessarily linearly convex. In fact, a compact or open set $E$ which is equal to one or several connected components of its linearly convex hull $E ^ { * * }$ is said to be weakly linearly convex. For an open set $E$, weak linear convexity amounts to the condition that through any boundary point $a \in \partial E$ there should pass a complex hyperplane not intersecting $E$, and this does not in general imply linear convexity of $E$. Any weakly linearly convex open set $E$ in $\mathbf{C} ^ { n }$ is pseudo-convex. |
| | | | |
| | ==Boundary properties.== | | ==Boundary properties.== |
| − | If a weakly linearly open set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001083.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001084.png" />, has a boundary of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001085.png" />, then it is automatically <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001086.png" />-convex. In particular, for bounded domains in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001087.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001088.png" /> boundary, the notions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001089.png" />-convexity, linear convexity and weak linear convexity all coincide. | + | If a weakly linearly open set in $\mathbf{P} ^ { n }$, $n > 1$, has a boundary of class $C ^ { 1 }$, then it is automatically $\mathbf{C}$-convex. In particular, for bounded domains in $\mathbf{C} ^ { n }$ with $C ^ { 1 }$ boundary, the notions of $\mathbf{C}$-convexity, linear convexity and weak linear convexity all coincide. |
| | | | |
| − | When the smoothness assumption is strengthened, so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001090.png" /> is given by a defining function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001091.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001092.png" />, then one considers the quadratic form | + | When the smoothness assumption is strengthened, so that $E = \{ z \in \mathbf C ^ { n } : \rho ( z ) < 0 \}$ is given by a defining function $\rho$ of class $C ^ { 2 }$, then one considers the quadratic form |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001093.png" /></td> </tr></table>
| + | \begin{equation*} H _ { \rho } ( a ; w ) = \end{equation*} |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001094.png" /></td> </tr></table>
| + | \begin{equation*} = 2 \operatorname { Re } \left( \sum _ { j ,\, k } \rho _ { j k } ( a ) w _ { j } w _ { k } \right) + 2 \sum _ { j ,\, k } \rho _ { j \overline { k } } ( a ) w _ { j } \overline { w } _ { k }, \end{equation*} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001095.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001096.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001097.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001098.png" />. This quadratic form is called the Hessian of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001099.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010100.png" />, whereas its Hermitian part | + | where $a \in \partial E$, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c12001096.png"/>, $\rho _ { j k } = \partial ^ { 2 } \rho / \partial z _ { j } \partial z _ { k }$, and $\rho _ { j \overline { k } } = \partial ^ { 2 } \rho / \partial z _ { j } \partial \overline{z} _ { k }$. This quadratic form is called the Hessian of $\rho$ at $a$, whereas its Hermitian part |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010101.png" /></td> </tr></table>
| + | \begin{equation*} L _ { \rho } ( a ; w ) = \sum _ { j , k } \rho _ { j \overline { k } } ( a ) w _ { j } \overline { w } _ { k } \end{equation*} |
| | | | |
| − | is called the Levi form (cf. also [[Hessian of a function|Hessian of a function]]). A smoothly bounded domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010102.png" /> is convex if and only if the Hessian of its defining function is positive semi-definite when restricted to the real tangent plane at any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010103.png" />. Similarly, a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010104.png" /> is pseudo-convex precisely if the restriction of the Levi form to the complex tangent plane is positive semi-definite. The notion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010105.png" />-convexity lies in between: A domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010106.png" /> with boundary of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010107.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010108.png" />-convex if and only if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010109.png" /> the Hessian is positive semi-definite on the complex tangent plane at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010110.png" />. | + | is called the Levi form (cf. also [[Hessian of a function|Hessian of a function]]). A smoothly bounded domain $E$ is convex if and only if the Hessian of its defining function is positive semi-definite when restricted to the real tangent plane at any $a \in \partial E$. Similarly, a domain $E$ is pseudo-convex precisely if the restriction of the Levi form to the complex tangent plane is positive semi-definite. The notion of $\mathbf{C}$-convexity lies in between: A domain $E \subset \mathbf{P} ^ { n }$ with boundary of class $C ^ { 2 }$ is $\mathbf{C}$-convex if and only if for any $a \in \partial E$ the Hessian is positive semi-definite on the complex tangent plane at $a$. |
| | | | |
| − | A complex hyperplane is said to be a tangent plane to an arbitrary open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010111.png" /> if it intersects the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010112.png" /> but not <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010113.png" /> itself. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010114.png" />, a connected open set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010115.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010116.png" />-convex if and only if, for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010117.png" />, the set of complex tangent planes to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010118.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010119.png" /> is a non-empty connected subset of the dual complement <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010120.png" />. | + | A complex hyperplane is said to be a tangent plane to an arbitrary open set $E \subset \mathbf{C} ^ { n }$ if it intersects the boundary $\partial E$ but not $E$ itself. When $n > 1$, a connected open set $E$ is $\mathbf{C}$-convex if and only if, for any $a \in \partial E$, the set of complex tangent planes to $E$ at $a$ is a non-empty connected subset of the dual complement $E ^ { * }$. |
| | | | |
| | ==Fantappiè transform.== | | ==Fantappiè transform.== |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010121.png" /> is an open (or compact) subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010122.png" />, one denotes by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010123.png" /> the [[Vector space|vector space]] of holomorphic functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010124.png" />, endowed with the projective (respectively, inductive) limit topology. An element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010125.png" /> of the dual space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010126.png" /> is called an analytic functional on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010127.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010128.png" /> contains the origin, then any hyperplane not intersecting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010129.png" /> is of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010130.png" />, and the Fantappiè transform <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010131.png" /> is defined to be the element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010132.png" /> given by | + | If $E$ is an open (or compact) subset of $\mathbf{C} ^ { n }$, one denotes by $A ( E )$ the [[Vector space|vector space]] of holomorphic functions on $E$, endowed with the projective (respectively, inductive) limit topology. An element $\mu$ of the dual space $A ^ { \prime } ( E )$ is called an analytic functional on $E$. If $E$ contains the origin, then any hyperplane not intersecting $E$ is of the form $\{ z \in \mathbf{C} ^ { n } : 1 + \langle z , \zeta \rangle \neq 0 \}$, and the Fantappiè transform $\tilde{\pi}$ is defined to be the element of $A ( E ^ { * } )$ given by |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010133.png" /></td> </tr></table>
| + | \begin{equation*} \widetilde{\mu} ( \zeta ) = \mu \left( \frac { 1 } { ( 1 + \langle \cdot , \zeta \rangle ) } \right). \end{equation*} |
| | | | |
| − | Now, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010134.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010135.png" />-convex, then the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010136.png" /> provides a topological isomorphism between the spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010137.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010138.png" />. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010139.png" /> there is a converse: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010140.png" /> is holomorphically convex and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010141.png" /> is bijective, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010142.png" /> must in fact be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010143.png" />-convex. Cf. [[Duality in complex analysis|Duality in complex analysis]]. | + | Now, if $E$ is $\mathbf{C}$-convex, then the mapping $\mu \mapsto \tilde{\mu}$ provides a topological isomorphism between the spaces $A ^ { \prime } ( E )$ and $A ( E ^ { * } )$. For $n > 1$ there is a converse: If $E$ is holomorphically convex and if $\mu \mapsto \tilde{\mu}$ is bijective, then $E$ must in fact be $\mathbf{C}$-convex. Cf. [[Duality in complex analysis|Duality in complex analysis]]. |
| | | | |
| − | The surjectivity of the Fantappiè transform is closely related to integral representation formulas for holomorphic functions (cf. also [[Information-based complexity|Integral representations in multi-dimensional complex analysis]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010144.png" /> be holomorphic in a neighbourhood of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010145.png" />-convex compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010146.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010147.png" /> be a smoothly bounded small open neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010148.png" />. By the Michael selection theorem one may choose, for every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010149.png" />, a hyperplane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010150.png" /> depending in a smooth way on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010151.png" />. Letting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010152.png" /> also denote the [[Differential form|differential form]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010153.png" />, one then has the Cauchy–Fantappiè formula | + | The surjectivity of the Fantappiè transform is closely related to integral representation formulas for holomorphic functions (cf. also [[Information-based complexity|Integral representations in multi-dimensional complex analysis]]). Let $f$ be holomorphic in a neighbourhood of a $\mathbf{C}$-convex compact set $E$, and let $\Omega$ be a smoothly bounded small open neighbourhood of $E$. By the Michael selection theorem one may choose, for every $\zeta \in \partial \Omega$, a hyperplane $s ( \zeta ) \in E ^ { * }$ depending in a smooth way on $\zeta$. Letting $s$ also denote the [[Differential form|differential form]] $s _ { 1 } ( \zeta ) d \zeta _ { 1 } + \ldots + s _ { n } ( \zeta ) d \zeta _ { n }$, one then has the Cauchy–Fantappiè formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010154.png" /></td> </tr></table>
| + | \begin{equation*} f ( z ) = \frac { 1 } { ( 2 \pi i ) ^ { n } } \int _ { \partial \Omega } \frac { f ( \zeta ) s \wedge ( \overline { \partial } s ) ^ { n - 1 } } { \langle \zeta - z , s \rangle ^ { n } } ,\; z \in E. \end{equation*} |
| | | | |
| − | Here, the integral kernel is homogeneous in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010155.png" />, so one can replace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010156.png" /> by the new section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010157.png" /> and then obtain | + | Here, the integral kernel is homogeneous in $s$, so one can replace $s$ by the new section $\sigma = - s / \langle s , \zeta \rangle$ and then obtain |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010158.png" /></td> </tr></table>
| + | \begin{equation*} f ( z ) = \frac { 1 } { ( 2 \pi i ) ^ { n } } \int _ { \partial \Omega } \frac { f ( \zeta ) \sigma \wedge ( \overline { \partial } \sigma ) ^ { n - 1 } } { ( 1 + \langle z , \sigma \rangle ) ^ { n } } ,\, z \in E. \end{equation*} |
| | | | |
| − | This integral formula has the following discrete analogue: Any function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010159.png" />, holomorphic in a neighbourhood of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010160.png" />-convex compact set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010161.png" />, has a decomposition into partial fractions | + | This integral formula has the following discrete analogue: Any function $f$, holomorphic in a neighbourhood of a $\mathbf{C}$-convex compact set $E \ni 0$, has a decomposition into partial fractions |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010162.png" /></td> </tr></table>
| + | \begin{equation*} f ( z ) = \sum _ { k = 1 } ^ { \infty } \frac { c _ { k } } { ( 1 + \langle z , \alpha _ { k } \rangle ) ^ { n } }, \end{equation*} |
| | | | |
| − | where all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010163.png" /> are contained in some compact subset of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010164.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010165.png" />. Hence the series converges uniformly in a neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010166.png" />. | + | where all $a_k$ are contained in some compact subset of $E ^ { * }$, and $\sum | c_k| < \infty$. Hence the series converges uniformly in a neighbourhood of $E$. |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010167.png" /> is only assumed to be weakly linearly convex, then the partial fraction representation becomes | + | If $E$ is only assumed to be weakly linearly convex, then the partial fraction representation becomes |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010168.png" /></td> </tr></table>
| + | \begin{equation*} f ( z ) = \sum _ { k = 1 } ^ { \infty } \frac { c _ { k } } { ( 1 + \langle z , a _ { k 1 } \rangle ) \ldots ( 1 + \langle z , a _ { k n } \rangle ) }, \end{equation*} |
| | | | |
| − | again with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010169.png" /> and uniform convergence in a neighbourhood of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010170.png" />. Conversely, any holomorphically convex compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010171.png" /> admitting such representations must necessarily be weakly linearly convex. | + | again with $\sum | c_k|< \infty$ and uniform convergence in a neighbourhood of $E$. Conversely, any holomorphically convex compact $E$ admitting such representations must necessarily be weakly linearly convex. |
| | | | |
| | ==Existence of primitive functions.== | | ==Existence of primitive functions.== |
| − | For any vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010172.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010173.png" /> denote the first-order differential operator | + | For any vector $a \in \mathbf{C} ^ { n } \backslash \{ 0 \}$, let $( a , \partial )$ denote the first-order differential operator |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010174.png" /></td> </tr></table>
| + | \begin{equation*} f \mapsto \sum _ { k = 1 } ^ { n } a _ { k } \frac { \partial f } { \partial z _ { k } }. \end{equation*} |
| | | | |
| − | This directional derivative can, of course, be viewed as a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010175.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010176.png" /> is any domain in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010177.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010178.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010179.png" />-convex, then this mapping is surjective for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010180.png" />, and conversely, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010181.png" /> is bounded and the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010182.png" /> is surjective for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010183.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010184.png" /> must be <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010185.png" />-convex. More generally, consider any [[Linear differential operator|linear differential operator]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010186.png" /> with constant coefficients, not all equal to zero, and regard it as a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010187.png" />. Then, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010188.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010189.png" />-convex, this mapping is surjective. | + | This directional derivative can, of course, be viewed as a mapping $A ( E ) \rightarrow A ( E )$, where $E$ is any domain in $\mathbf{C} ^ { n }$. If $E$ is $\mathbf{C}$-convex, then this mapping is surjective for any $a$, and conversely, if $E$ is bounded and the mapping $f \mapsto \langle a , \partial \rangle f$ is surjective for each $a$, then $E$ must be $\mathbf{C}$-convex. More generally, consider any [[Linear differential operator|linear differential operator]] $P ( \partial ) = P ( \partial / \partial z _ { 1 } , \dots , \partial / \partial z _ { n } )$ with constant coefficients, not all equal to zero, and regard it as a mapping $A ( E ) \rightarrow A ( E )$. Then, if $E$ is $\mathbf{C}$-convex, this mapping is surjective. |
| | | | |
| − | ==<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010190.png" />-convexity in other contexts.== | + | ==$\mathbf{C}$-convexity in other contexts.== |
| − | Sets that are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010191.png" />-convex occur naturally in several other connections, such as in complex polynomial approximation (in particular, in so-called [[Kergin interpolation|Kergin interpolation]]), invariant metrics and pluri-potential theory, for instance in the work of L. Lempert. The fact that the dual complement of a convex set in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010192.png" /> is not necessarily convex, but only <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010193.png" />-convex, is also a motivation for considering <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010194.png" />-convex sets. | + | Sets that are $\mathbf{C}$-convex occur naturally in several other connections, such as in complex polynomial approximation (in particular, in so-called [[Kergin interpolation|Kergin interpolation]]), invariant metrics and pluri-potential theory, for instance in the work of L. Lempert. The fact that the dual complement of a convex set in $\mathbf{C} ^ { n }$ is not necessarily convex, but only $\mathbf{C}$-convex, is also a motivation for considering $\mathbf{C}$-convex sets. |
| | | | |
| | ==Terminology.== | | ==Terminology.== |
| − | There is a certain confusion in the literature as to the terminology connected with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010195.png" />-convexity and the related convexity notions. The first ones to study weak linear convexity were H. Behnke and E. Peschl [[#References|[a4]]], who used the term Planarkonvexität. Later, A. Martineau [[#References|[a8]]] introduced the term convexité linéelle for what is here called linear convexity. At about the same time, L. Aizenberg [[#References|[a2]]] and his school in Krasnoyarsk took up the Russian expression lineinaya vypuklost', which in English translations became "linear convexity" , to denote what is here called weak linear convexity. Some authors prefer to use the English adjective "lineal" rather than linear in this context, stressing the fact that the (original) French term is "linéel" and not "linéaire" . Until the 1990s, strong linear convexity was the term used for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010196.png" />-convexity, whereas projective complement and conjugate set were used as synonyms for the dual complement <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010197.png" />. In the above, the terminology adopted by L.V. Hörmander [[#References|[a6]]] is followed. | + | There is a certain confusion in the literature as to the terminology connected with $\mathbf{C}$-convexity and the related convexity notions. The first ones to study weak linear convexity were H. Behnke and E. Peschl [[#References|[a4]]], who used the term Planarkonvexität. Later, A. Martineau [[#References|[a8]]] introduced the term convexité linéelle for what is here called linear convexity. At about the same time, L. Aizenberg [[#References|[a2]]] and his school in Krasnoyarsk took up the Russian expression lineinaya vypuklost', which in English translations became "linear convexity" , to denote what is here called weak linear convexity. Some authors prefer to use the English adjective "lineal" rather than linear in this context, stressing the fact that the (original) French term is "linéel" and not "linéaire" . Until the 1990s, strong linear convexity was the term used for $\mathbf{C}$-convexity, whereas projective complement and conjugate set were used as synonyms for the dual complement $E ^ { * }$. In the above, the terminology adopted by L.V. Hörmander [[#References|[a6]]] is followed. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Aizenberg, "Decomposition of holomorphic functions of several complex variables into partial fractions" ''Sib. Math. J.'' , '''8''' (1967) pp. 859–872</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Aizenberg, "Linear convexity in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010198.png" /> and the separation of singularities of holomorphic functions" ''Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys.'' , '''15''' (1967) pp. 487–495 (In Russian) (French summary)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Andersson, M. Passare, R. Sigurdsson, "Complex convexity and analytic functionals I" ''Science Inst. Univ. Iceland Preprint'' , '''June''' (1995)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Behnke, E. Peschl, "Zur Theorie der Funktionen mehrerer komplexer Veränderlichen. Konvexität in bezug auf analytische Ebenen im kleinen und grossen" ''Math. Ann.'' , '''111''' (1935) pp. 158–177</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S.G. Gindikin, G.M. Henkin, "Integral geometry for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010199.png" />-cohomologies in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010200.png" />-linearly concave domains in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010201.png" />" ''Funct. Anal. Appl.'' , '''12''' (1978) pp. 247–261</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> L. Hörmander, "Notions of convexity" , ''Progr. Math.'' , '''127''' , Birkhäuser (1994)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> C.O. Kiselman, "A differential inequality characterizing weak lineal convexity" ''Math. Ann.'' , '''311''' (1998) pp. 1–10</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> A. Martineau, "Sur la topologie des espaces de fonctions holomorphes" ''Math. Ann.'' , '''163''' (1966) pp. 62–88</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> A. Martineau, "Sur la notion d'ensemble fortement linéellement convexe" ''An. Acad. Brasil. Ci.'' , '''40''' (1968) pp. 427–435</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> S.V. Znamenskii, "A geometric criterion for strong linear convexity" ''Funct. Anal. Appl.'' , '''13''' (1979) pp. 224–225</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> S.V. Znamenskii, L.N. Znamenskaya, "Spiral connectedness of the sections and projections of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120010/c120010202.png" />-convex sets" ''Math. Notes'' , '''59''' (1996) pp. 253–260</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> L. Aizenberg, "Decomposition of holomorphic functions of several complex variables into partial fractions" ''Sib. Math. J.'' , '''8''' (1967) pp. 859–872</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> L. Aizenberg, "Linear convexity in $\mathbf{C} ^ { n }$ and the separation of singularities of holomorphic functions" ''Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys.'' , '''15''' (1967) pp. 487–495 (In Russian) (French summary)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> M. Andersson, M. Passare, R. Sigurdsson, "Complex convexity and analytic functionals I" ''Science Inst. Univ. Iceland Preprint'' , '''June''' (1995)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H. Behnke, E. Peschl, "Zur Theorie der Funktionen mehrerer komplexer Veränderlichen. Konvexität in bezug auf analytische Ebenen im kleinen und grossen" ''Math. Ann.'' , '''111''' (1935) pp. 158–177 {{MR|1512986}} {{ZBL|0011.16903}} {{ZBL|61.0373.01}} </td></tr><tr><td valign="top">[a5]</td> <td valign="top"> S.G. Gindikin, G.M. Henkin, "Integral geometry for $\overline { \partial }$-cohomologies in $q$-linearly concave domains in $\mathbf{CP} ^ { n }$" ''Funct. Anal. Appl.'' , '''12''' (1978) pp. 247–261</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> L. Hörmander, "Notions of convexity" , ''Progr. Math.'' , '''127''' , Birkhäuser (1994) {{MR|1301332}} {{ZBL|0835.32001}} </td></tr><tr><td valign="top">[a7]</td> <td valign="top"> C.O. Kiselman, "A differential inequality characterizing weak lineal convexity" ''Math. Ann.'' , '''311''' (1998) pp. 1–10 {{MR|1624326}} {{ZBL|0911.32031}} </td></tr><tr><td valign="top">[a8]</td> <td valign="top"> A. Martineau, "Sur la topologie des espaces de fonctions holomorphes" ''Math. Ann.'' , '''163''' (1966) pp. 62–88 {{MR|0190697}} {{ZBL|0138.38101}} </td></tr><tr><td valign="top">[a9]</td> <td valign="top"> A. Martineau, "Sur la notion d'ensemble fortement linéellement convexe" ''An. Acad. Brasil. Ci.'' , '''40''' (1968) pp. 427–435 {{MR|0282292}} {{ZBL|}} </td></tr><tr><td valign="top">[a10]</td> <td valign="top"> S.V. Znamenskii, "A geometric criterion for strong linear convexity" ''Funct. Anal. Appl.'' , '''13''' (1979) pp. 224–225 {{MR|545375}} {{ZBL|}} </td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S.V. Znamenskii, L.N. Znamenskaya, "Spiral connectedness of the sections and projections of $\mathbf{C}$-convex sets" ''Math. Notes'' , '''59''' (1996) pp. 253–260</td></tr></table> |
convexity in complex analysis
A domain or compact subset $E$ in $\mathbf{C} ^ { n }$ is said to be $\mathbf{C}$-convex if for any complex line $\operatorname{l} \subset \mathbf{C} ^ { n }$ the intersection $E \cap \bf l$ is both connected and simply connected (meaning that its complement in the Riemann sphere $\text{l} \cup \{ \infty \}$ is connected; cf. also Connected set; Simply-connected domain). The notion of $\mathbf{C}$-convexity is an intermediate one, in the sense that any geometrically convex set is necessarily $\mathbf{C}$-convex, whereas $\mathbf{C}$-convexity implies holomorphic convexity (or pseudo-convexity; cf. also Pseudo-convex and pseudo-concave). In particular, a real subset $E$ in $\mathbf{R} ^ { n } \subset \mathbf{C} ^ { n }$ is $\mathbf{C}$-convex if and only if it is convex in the ordinary, geometrical, sense. Open or compact $\mathbf{C}$-convex subsets are in several respects the natural sets when it comes to studying properties of holomorphic functions that are invariant under affine (or projective) transformations. They often play a role analogous to that of convex sets in real analysis.
Topology of $\mathbf{C}$-convex sets.
Any $\mathbf{C}$-convex domain is homeomorphically equivalent to the open unit ball $| z _ { 1 } | ^ { 2 } + \ldots + | z _ { n } | ^ { 2 } < 1$, and a compact $\mathbf{C}$-convex set $E$ is also topologically simple in the sense that it has vanishing reduced cohomology:
\begin{equation*} H ^ { 0 } ( E ) = \mathbf{Z} , \quad H ^ { p } ( E ) = 0 , p > 0. \end{equation*}
The operations of forming the closure and the interior are not well-adapted to $\mathbf{C}$-convexity. There exist, e.g., compact $\mathbf{C}$-convex sets with non-connected interior. Also, the intersection of two $\mathbf{C}$-convex sets is not necessarily $\mathbf{C}$-convex.
Projective invariance.
It is natural to consider a $\mathbf{C}$-convex set $E \subset \mathbf{C} ^ { n }$ also as a subset of the complex projective space $\mathbf{P} ^ { n } \supset \mathbf{C} ^ { n }$. Each non-trivial complex linear mapping $\tilde{T} : {\bf C} ^ { m + 1 } \rightarrow {\bf C} ^ { n + 1 }$ descends to a mapping $T : \mathbf{P} ^ { m } \backslash X \rightarrow \mathbf{P} ^ { n }$, where $X$ corresponds to the kernel of $\tilde{T}$. The mapping $T$ is then called a projective transformation, and $\mathbf{C}$-convexity is invariant under any such transformation: If $E$ and $F$ are $\mathbf{C}$-convex subsets of ${\bf P} ^ { m } \backslash X$ and $\mathbf{P} ^ { n }$, respectively, then both $T ( E )$ and $T ^ { - 1 } ( F )$ are also $\mathbf{C}$-convex.
A $\mathbf{C}$-convex set $E \subset {\bf C} ^ { n } \subset {\bf P} ^ { n }$ is said to be non-degenerate if it is not of the form $T ( F )$ or $T ^ { - 1 } ( F )$, where $F \subset \mathbf{P} ^ { n - 1 }$ and $T$ is a projective transformation. Examples of degenerate $\mathbf{C}$-convex sets are those that are contained in complex hyperplanes, or of the form $E \times \mathbf C$. It is an interesting fact that far from all one-dimensional $\mathbf{C}$-convex sets can occur as the intersection of a multi-dimensional non-degenerate $\mathbf{C}$-convex set with a complex line.
Dual complement and linear convexity.
If $E$ is any subset of $\mathbf{C} ^ { n } \subset \mathbf{P} ^ { n }$, then its dual complement $E ^ { * }$ is, by definition, the collection of all complex hyperplanes that do not intersect $E$. When $n = 1$ this is just the usual complement of a set in the Riemann sphere, and in higher dimensions $E ^ { * }$ can be considered as a subset of the dual projective space ${\bf P}^ { n^* }$. If $E$ is an open (or compact) $\mathbf{C}$-convex set, then its dual complement $E ^ { * }$ is a compact (respectively, open) $\mathbf{C}$-convex set. Moreover, such a $\mathbf{C}$-convex set $E$ is also linearly convex in the sense that $E = E ^ { * * }$, i.e. the complement of $E$ is a union of complex hyperplanes. There are, however, many linearly convex sets that are not $\mathbf{C}$-convex. For instance, any Cartesian product of subsets of $\mathbf{C}$ is linearly convex, but it is $\mathbf{C}$-convex only if each factor is convex in the usual sense. A connected component of a linearly convex set $E$ is not necessarily linearly convex. In fact, a compact or open set $E$ which is equal to one or several connected components of its linearly convex hull $E ^ { * * }$ is said to be weakly linearly convex. For an open set $E$, weak linear convexity amounts to the condition that through any boundary point $a \in \partial E$ there should pass a complex hyperplane not intersecting $E$, and this does not in general imply linear convexity of $E$. Any weakly linearly convex open set $E$ in $\mathbf{C} ^ { n }$ is pseudo-convex.
Boundary properties.
If a weakly linearly open set in $\mathbf{P} ^ { n }$, $n > 1$, has a boundary of class $C ^ { 1 }$, then it is automatically $\mathbf{C}$-convex. In particular, for bounded domains in $\mathbf{C} ^ { n }$ with $C ^ { 1 }$ boundary, the notions of $\mathbf{C}$-convexity, linear convexity and weak linear convexity all coincide.
When the smoothness assumption is strengthened, so that $E = \{ z \in \mathbf C ^ { n } : \rho ( z ) < 0 \}$ is given by a defining function $\rho$ of class $C ^ { 2 }$, then one considers the quadratic form
\begin{equation*} H _ { \rho } ( a ; w ) = \end{equation*}
\begin{equation*} = 2 \operatorname { Re } \left( \sum _ { j ,\, k } \rho _ { j k } ( a ) w _ { j } w _ { k } \right) + 2 \sum _ { j ,\, k } \rho _ { j \overline { k } } ( a ) w _ { j } \overline { w } _ { k }, \end{equation*}
where $a \in \partial E$, 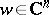 , $\rho _ { j k } = \partial ^ { 2 } \rho / \partial z _ { j } \partial z _ { k }$, and $\rho _ { j \overline { k } } = \partial ^ { 2 } \rho / \partial z _ { j } \partial \overline{z} _ { k }$. This quadratic form is called the Hessian of $\rho$ at $a$, whereas its Hermitian part
, $\rho _ { j k } = \partial ^ { 2 } \rho / \partial z _ { j } \partial z _ { k }$, and $\rho _ { j \overline { k } } = \partial ^ { 2 } \rho / \partial z _ { j } \partial \overline{z} _ { k }$. This quadratic form is called the Hessian of $\rho$ at $a$, whereas its Hermitian part
\begin{equation*} L _ { \rho } ( a ; w ) = \sum _ { j , k } \rho _ { j \overline { k } } ( a ) w _ { j } \overline { w } _ { k } \end{equation*}
is called the Levi form (cf. also Hessian of a function). A smoothly bounded domain $E$ is convex if and only if the Hessian of its defining function is positive semi-definite when restricted to the real tangent plane at any $a \in \partial E$. Similarly, a domain $E$ is pseudo-convex precisely if the restriction of the Levi form to the complex tangent plane is positive semi-definite. The notion of $\mathbf{C}$-convexity lies in between: A domain $E \subset \mathbf{P} ^ { n }$ with boundary of class $C ^ { 2 }$ is $\mathbf{C}$-convex if and only if for any $a \in \partial E$ the Hessian is positive semi-definite on the complex tangent plane at $a$.
A complex hyperplane is said to be a tangent plane to an arbitrary open set $E \subset \mathbf{C} ^ { n }$ if it intersects the boundary $\partial E$ but not $E$ itself. When $n > 1$, a connected open set $E$ is $\mathbf{C}$-convex if and only if, for any $a \in \partial E$, the set of complex tangent planes to $E$ at $a$ is a non-empty connected subset of the dual complement $E ^ { * }$.
Fantappiè transform.
If $E$ is an open (or compact) subset of $\mathbf{C} ^ { n }$, one denotes by $A ( E )$ the vector space of holomorphic functions on $E$, endowed with the projective (respectively, inductive) limit topology. An element $\mu$ of the dual space $A ^ { \prime } ( E )$ is called an analytic functional on $E$. If $E$ contains the origin, then any hyperplane not intersecting $E$ is of the form $\{ z \in \mathbf{C} ^ { n } : 1 + \langle z , \zeta \rangle \neq 0 \}$, and the Fantappiè transform $\tilde{\pi}$ is defined to be the element of $A ( E ^ { * } )$ given by
\begin{equation*} \widetilde{\mu} ( \zeta ) = \mu \left( \frac { 1 } { ( 1 + \langle \cdot , \zeta \rangle ) } \right). \end{equation*}
Now, if $E$ is $\mathbf{C}$-convex, then the mapping $\mu \mapsto \tilde{\mu}$ provides a topological isomorphism between the spaces $A ^ { \prime } ( E )$ and $A ( E ^ { * } )$. For $n > 1$ there is a converse: If $E$ is holomorphically convex and if $\mu \mapsto \tilde{\mu}$ is bijective, then $E$ must in fact be $\mathbf{C}$-convex. Cf. Duality in complex analysis.
The surjectivity of the Fantappiè transform is closely related to integral representation formulas for holomorphic functions (cf. also Integral representations in multi-dimensional complex analysis). Let $f$ be holomorphic in a neighbourhood of a $\mathbf{C}$-convex compact set $E$, and let $\Omega$ be a smoothly bounded small open neighbourhood of $E$. By the Michael selection theorem one may choose, for every $\zeta \in \partial \Omega$, a hyperplane $s ( \zeta ) \in E ^ { * }$ depending in a smooth way on $\zeta$. Letting $s$ also denote the differential form $s _ { 1 } ( \zeta ) d \zeta _ { 1 } + \ldots + s _ { n } ( \zeta ) d \zeta _ { n }$, one then has the Cauchy–Fantappiè formula
\begin{equation*} f ( z ) = \frac { 1 } { ( 2 \pi i ) ^ { n } } \int _ { \partial \Omega } \frac { f ( \zeta ) s \wedge ( \overline { \partial } s ) ^ { n - 1 } } { \langle \zeta - z , s \rangle ^ { n } } ,\; z \in E. \end{equation*}
Here, the integral kernel is homogeneous in $s$, so one can replace $s$ by the new section $\sigma = - s / \langle s , \zeta \rangle$ and then obtain
\begin{equation*} f ( z ) = \frac { 1 } { ( 2 \pi i ) ^ { n } } \int _ { \partial \Omega } \frac { f ( \zeta ) \sigma \wedge ( \overline { \partial } \sigma ) ^ { n - 1 } } { ( 1 + \langle z , \sigma \rangle ) ^ { n } } ,\, z \in E. \end{equation*}
This integral formula has the following discrete analogue: Any function $f$, holomorphic in a neighbourhood of a $\mathbf{C}$-convex compact set $E \ni 0$, has a decomposition into partial fractions
\begin{equation*} f ( z ) = \sum _ { k = 1 } ^ { \infty } \frac { c _ { k } } { ( 1 + \langle z , \alpha _ { k } \rangle ) ^ { n } }, \end{equation*}
where all $a_k$ are contained in some compact subset of $E ^ { * }$, and $\sum | c_k| < \infty$. Hence the series converges uniformly in a neighbourhood of $E$.
If $E$ is only assumed to be weakly linearly convex, then the partial fraction representation becomes
\begin{equation*} f ( z ) = \sum _ { k = 1 } ^ { \infty } \frac { c _ { k } } { ( 1 + \langle z , a _ { k 1 } \rangle ) \ldots ( 1 + \langle z , a _ { k n } \rangle ) }, \end{equation*}
again with $\sum | c_k|< \infty$ and uniform convergence in a neighbourhood of $E$. Conversely, any holomorphically convex compact $E$ admitting such representations must necessarily be weakly linearly convex.
Existence of primitive functions.
For any vector $a \in \mathbf{C} ^ { n } \backslash \{ 0 \}$, let $( a , \partial )$ denote the first-order differential operator
\begin{equation*} f \mapsto \sum _ { k = 1 } ^ { n } a _ { k } \frac { \partial f } { \partial z _ { k } }. \end{equation*}
This directional derivative can, of course, be viewed as a mapping $A ( E ) \rightarrow A ( E )$, where $E$ is any domain in $\mathbf{C} ^ { n }$. If $E$ is $\mathbf{C}$-convex, then this mapping is surjective for any $a$, and conversely, if $E$ is bounded and the mapping $f \mapsto \langle a , \partial \rangle f$ is surjective for each $a$, then $E$ must be $\mathbf{C}$-convex. More generally, consider any linear differential operator $P ( \partial ) = P ( \partial / \partial z _ { 1 } , \dots , \partial / \partial z _ { n } )$ with constant coefficients, not all equal to zero, and regard it as a mapping $A ( E ) \rightarrow A ( E )$. Then, if $E$ is $\mathbf{C}$-convex, this mapping is surjective.
$\mathbf{C}$-convexity in other contexts.
Sets that are $\mathbf{C}$-convex occur naturally in several other connections, such as in complex polynomial approximation (in particular, in so-called Kergin interpolation), invariant metrics and pluri-potential theory, for instance in the work of L. Lempert. The fact that the dual complement of a convex set in $\mathbf{C} ^ { n }$ is not necessarily convex, but only $\mathbf{C}$-convex, is also a motivation for considering $\mathbf{C}$-convex sets.
Terminology.
There is a certain confusion in the literature as to the terminology connected with $\mathbf{C}$-convexity and the related convexity notions. The first ones to study weak linear convexity were H. Behnke and E. Peschl [a4], who used the term Planarkonvexität. Later, A. Martineau [a8] introduced the term convexité linéelle for what is here called linear convexity. At about the same time, L. Aizenberg [a2] and his school in Krasnoyarsk took up the Russian expression lineinaya vypuklost', which in English translations became "linear convexity" , to denote what is here called weak linear convexity. Some authors prefer to use the English adjective "lineal" rather than linear in this context, stressing the fact that the (original) French term is "linéel" and not "linéaire" . Until the 1990s, strong linear convexity was the term used for $\mathbf{C}$-convexity, whereas projective complement and conjugate set were used as synonyms for the dual complement $E ^ { * }$. In the above, the terminology adopted by L.V. Hörmander [a6] is followed.
References
| [a1] | L. Aizenberg, "Decomposition of holomorphic functions of several complex variables into partial fractions" Sib. Math. J. , 8 (1967) pp. 859–872 |
| [a2] | L. Aizenberg, "Linear convexity in $\mathbf{C} ^ { n }$ and the separation of singularities of holomorphic functions" Bull. Acad. Polon. Sci. Ser. Math. Astr. Phys. , 15 (1967) pp. 487–495 (In Russian) (French summary) |
| [a3] | M. Andersson, M. Passare, R. Sigurdsson, "Complex convexity and analytic functionals I" Science Inst. Univ. Iceland Preprint , June (1995) |
| [a4] | H. Behnke, E. Peschl, "Zur Theorie der Funktionen mehrerer komplexer Veränderlichen. Konvexität in bezug auf analytische Ebenen im kleinen und grossen" Math. Ann. , 111 (1935) pp. 158–177 MR1512986 Zbl 0011.16903 Zbl 61.0373.01 |
| [a5] | S.G. Gindikin, G.M. Henkin, "Integral geometry for $\overline { \partial }$-cohomologies in $q$-linearly concave domains in $\mathbf{CP} ^ { n }$" Funct. Anal. Appl. , 12 (1978) pp. 247–261 |
| [a6] | L. Hörmander, "Notions of convexity" , Progr. Math. , 127 , Birkhäuser (1994) MR1301332 Zbl 0835.32001 |
| [a7] | C.O. Kiselman, "A differential inequality characterizing weak lineal convexity" Math. Ann. , 311 (1998) pp. 1–10 MR1624326 Zbl 0911.32031 |
| [a8] | A. Martineau, "Sur la topologie des espaces de fonctions holomorphes" Math. Ann. , 163 (1966) pp. 62–88 MR0190697 Zbl 0138.38101 |
| [a9] | A. Martineau, "Sur la notion d'ensemble fortement linéellement convexe" An. Acad. Brasil. Ci. , 40 (1968) pp. 427–435 MR0282292 |
| [a10] | S.V. Znamenskii, "A geometric criterion for strong linear convexity" Funct. Anal. Appl. , 13 (1979) pp. 224–225 MR545375 |
| [a11] | S.V. Znamenskii, L.N. Znamenskaya, "Spiral connectedness of the sections and projections of $\mathbf{C}$-convex sets" Math. Notes , 59 (1996) pp. 253–260 |
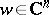 , $\rho _ { j k } = \partial ^ { 2 } \rho / \partial z _ { j } \partial z _ { k }$, and $\rho _ { j \overline { k } } = \partial ^ { 2 } \rho / \partial z _ { j } \partial \overline{z} _ { k }$. This quadratic form is called the Hessian of $\rho$ at $a$, whereas its Hermitian part
, $\rho _ { j k } = \partial ^ { 2 } \rho / \partial z _ { j } \partial z _ { k }$, and $\rho _ { j \overline { k } } = \partial ^ { 2 } \rho / \partial z _ { j } \partial \overline{z} _ { k }$. This quadratic form is called the Hessian of $\rho$ at $a$, whereas its Hermitian part