Duality in complex analysis

Let $D$ be a domain in $\mathbf{C} ^ { n }$ and denote by $A ( D )$ the space of all functions holomorphic in $D$ with the topology of uniform convergence on compact subsets of $D$ (the projective limit topology). Let $K$ be a compact set in $\mathbf{C} ^ { n }$. Similarly, let $A ( K )$ be the space of all functions holomorphic on $K$ endowed with the following topology: A sequence $\{ f_{m} \}$ converges to a function $f$ in $A ( K )$ if there exists a neighbourhood $U \supset K$ such that all the functions $f _ { m } ,\, f \in A ( U )$ and $\{ f_{m} \}$ converges to $f$ in $A ( U )$ (the inductive limit topology).

The description of the dual spaces $A ( D ) ^ { * }$ and $A ( K ) ^ { * }$ is one of the main problems in the concrete functional analysis of spaces of holomorphic functions.

Grothendieck–Köthe–Sebastião e Silva duality.

Let $D$ be a domain in the complex plane ${\bf C} ^ { 1 }$ and let

\begin{equation*} A _ { 0 } ( \overline { \mathbf{C} } \backslash D ) = \{ f : f \in A ( \overline { \mathbf{C} } \backslash D ) , f ( \infty ) = 0 \}. \end{equation*}

Then one has the isomorphism (see [a1], [a2], [a3])

\begin{equation*} A ( D ) ^ { * } \simeq A _ { 0 } ( \overline { \mathbf{C} } \backslash D ), \end{equation*}

defined by

\begin{equation} \tag{a1} F ( f ) = F _ { \phi } ( f ) = \int _ { \Gamma } f ( z ) \phi ( z ) d z, \end{equation}

where $\phi \in A _ { 0 } ( \overline { \mathbf{C} } \backslash D )$. Here, $\phi \in A _ { 0 } ( Q )$, where $\overline { \mathbf{C} } \backslash D \subset Q$ for some domain $Q$; and the curve $\Gamma \subset D \cap Q$ separates the singularities of the functions $f \in A ( D )$ and $\phi$. The integral in (a1) does not depend on the choice of $\Gamma$.

Duality and linear convexity.

When $n > 1$, the complement of a bounded domain $D \subset \mathbf{C} ^ { x }$ is not useful for function theory. Indeed, if $f \in A _ { 0 } ( \overline { \mathbf{C} } ^ { n } \backslash D )$, then $f \equiv 0$. However, a generalized notion of "exterior" does exist for linearly convex domains and compacta.

A domain $D \subset \mathbf{C} ^ { x }$ is called linearly convex if for any $\zeta \in \partial D$ there exists a complex hyperplane 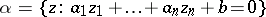through $\zeta$ that does not intersect $D$. A compact set $K \subset \mathbf{C} ^ { n }$ is called linearly convex if it can be approximated from the outside by linearly convex domains. Observe that the topological dimension of $\alpha$ is $2 n - 2$.

Some examples:

1) Let $D$ be convex; then for any point $\zeta$ of the boundary $\partial D$ there exists a hyperplane of support $\beta$ of dimension $2 n - 1$ that contains the complex hyperplane $\alpha$.

2) Let $D = D _ { 1 } \times \ldots \times D _ { n }$, where $D_{j} \subset {\bf C} ^ { 1 }$, $j = 1 , \ldots , n$, are arbitrary plane domains.

Let $D$ be approximated from within by the sequence of linearly convex domains $\{ D _ { m } \}$ with smooth boundaries: $\overline { D } _ { m } \subset D _ { m + 1 } \subset D$, where $D _ { m } = \{ z : \Phi ^ { m } ( z , \bar{z} ) < 0 \}$, $\Phi ^ { m } \in C ^ { 2 } ( \overline { D } _ { m } )$, and $\operatorname { grad } \Phi ^ { m } | _ { \partial D _ { m } } \neq 0$. Such an approximation does not always exist, unlike the case of usual convexity. For instance, this approximation is impossible in Example 2) if at least one of the domains $D _ { j }$ is non-convex.

If $0 \in D$, one has the isomorphism

\begin{equation*} A ( D ) ^ { * } \simeq A ( \tilde { D } ), \end{equation*}

where $\tilde { D } = \{ w : w _ { 1 } z _ { 1 } + \ldots + w _ { n } z _ { n } \neq 1 , z \in D \}$ is the adjoint set (the generalized complement) defined by

\begin{equation} \tag{a2} F ( t ) = F _ { \phi } ( f ) = \int _ { \partial D _ { m } } f ( z ) \phi ( w ) \omega ( z , w ). \end{equation}

Here, $f \in A ( D )$, $\phi \in A ( \widetilde { D } )$,

\begin{equation*} w _ { j } = \frac { \Phi ^ { \prime z _ { j } } } { \langle \operatorname { grad } _ { z } \Phi , z \rangle } ,\; j = 1 , \ldots , n, \end{equation*}

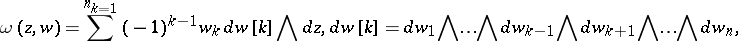\begin{equation*} d z = d z _ { 1 } \bigwedge \ldots \bigwedge d z _ { n } , \quad \langle a , b \rangle = a _ { 1 } b _ { 1 } + \ldots + a _ { n } b _ { n }. \end{equation*}

The index $m$ depends on the function $\phi$, which is holomorphic on the larger compact set $\widetilde { D } _ { m } \supset \widetilde { D }$. The integral in (a4) does not depend on the choice of $m$.

A similar duality is valid for the space $A ( K )$ as well (see [a4], [a5], [a6]).

A. Martineau has defined a strongly linearly convex domain $D$ to be a linearly convex domain for which the above-mentioned isomorphism holds. It is proved in [a7] that a domain $D$ is strongly linearly convex if and only if the intersection of $D$ with any complex line is connected and simply connected (see also [a8], [a9], [a10], [a11]).

Duality based on regularized integration over the boundary.

L. Stout obtained the following result for bounded domains $D \subset \mathbf{C} ^ { x }$ with the property that, for a fixed $z \in D$, the Szegö kernel $K ( z , \zeta )$ is real-analytic in $\zeta \in \partial D$. Apparently, this is true if $D$ is a strictly pseudo-convex domain with real-analytic boundary. Then the isomorphism

\begin{equation} \tag{a3} A ( D ) ^ { * } \simeq A ( \overline { D } ) \end{equation}

is defined by the formula

\begin{equation*} F ( f ) = F _ { \phi } ( f ) = \operatorname { lim } _ { \epsilon \rightarrow 0 } \int _ { \partial D _ { \epsilon } } f ( z ) \overline { \phi ( z ) } d \sigma, \end{equation*}

where $D _ { \epsilon } = \{ z : z \in D , \rho ( z , \partial D ) > \epsilon \}$, $f \in A ( D )$, $\phi \in A ( \overline { D } )$ (see [a12], [a13]).

Nacinovich–Shlapunov–Tarkhanov theorem.

Let $D$ be a bounded domain in $\mathbf{C} ^ { n }$ with real-analytic boundary and with the property that any neighbourhood $U$ of $\overline{ D }$ contains a neighbourhood $U ^ { \prime } \subset U$ such that $A ( U ^ { \prime } )$ is dense in $A ( D )$. This is always the case if $D$ is a strictly pseudo-convex domain with real-analytic boundary.

For any function $\phi \in A ( \overline { D } )$ there exists a unique solution of the Dirichlet problem

\begin{equation*} \left\{ \begin{array} { l } { \Delta v = 0 } & {\text{in} \ \mathbf{C}^{n} \setminus \overline{D}, }\\ { v = \phi} & { \text { on } \partial D, } \\ { | v | \leq \frac { c } { | z | ^ { 2 n - 2 } }. } \end{array} \right. \end{equation*}

Here, the isomorphism (a3) can be defined by the formula (see [a14])

\begin{equation} \tag{a4} F (\, f ) = F _ { \phi } (\, f ) = \int _ { \partial D _ { m } } f ( z ) \sum ^ { n } _ { k = 1 } ( - 1 ) ^ { k - 1 } \frac { \partial \overline{ v } } { \partial z _ { k } } d \overline{z} [ k ] \bigwedge d z. \end{equation}

The integral is well-defined for some $m$ (where $\{ D _ { m } \}$ is a sequence of domains with smooth boundaries which approximate $D$ from within) since the function $v$, which is harmonic in $\mathbf{C} ^ { n } \backslash \overline { D }$, can be harmonically continued into for some $m$ because of the real analyticity of $\partial D$ and $\phi |_{\partial D}$. The integral in (a4) does not depend on the choice of $m$.

Duality and cohomology.

Let $H ^ { n , n - 1 } ( {\bf C} ^ { n } \backslash D )$ be the Dolbeault cohomology space

\begin{equation*} H ^ { n , n - 1 } = Z ^ { n , n - 1 } / B ^ { n , n - 1 }, \end{equation*}

where $Z ^ { n , n - 1 }$ is the space of all $\overline { \partial }$-closed forms $\alpha$ that are in $C ^ { \infty }$ on some neighbourhood $U$ of $\mathbf{C} ^ { n } \backslash D$ (the neighbourhood depends on the cocycle $\alpha$) and $B ^ { n ,\, n - 1 }$ is the subspace of $Z ^ { n , n - 1 }$ of all $\overline { \partial }$-exact forms $\alpha$ (coboundaries).

If $D$ is a bounded pseudo-convex domain, then one has [a15], [a16] an isomorphism

\begin{equation*} A ( D ) ^ { * } \simeq H ^ { n , n - 1 } ( \mathbf{C} ^ { n } \backslash D ), \end{equation*}

defined by the formula

\begin{equation} \tag{a5} F ( f ) = F _ { g } ( f ) = \int _ { \partial D _ { m } } f g, \end{equation}

where $f \in A ( D )$, $g \in H ^ { n ,\, n - 1 } ( \mathbf{C} ^ { n } \backslash D )$. Here, for some $U \supset \mathbf{C} ^ { n } \backslash D$ one has $g \in H ^ { n , n - 1 } ( U )$; $\{ D _ { m } \}$ is a sequence of domains with smooth boundaries approximating $D$ from within. Although $m$ depends on the choice of $U$, the integral in (a5) does not depend on $m$ (given (a5), the same formula is valid for larger $m$ as well).

A new result [a17] consists of the following: Let $D$ be a bounded pseudo-convex domain in $\mathbf{C} ^ { n }$ that can be approximated from within by a sequence of strictly pseudo-convex domains $\{ D _ { m } \}$; and let $A$ be the subspace of $Z ^ { n , n - 1 }$ consisting of the differential forms of type

\begin{equation} \tag{a6} g _ { u } = \sum _ { k = 1 } ^ { n } ( - 1 ) ^ { k - 1 } \frac { \partial u } { \partial z _ { k } } d \bar{z} [ k ] \wedge d z, \end{equation}

where $u$ is a function that is harmonic in some neighbourhood $U$ of $\mathbf{C} ^ { n } \backslash D$ (which depends on $u$) such that

\begin{equation*} | u ( z ) | \leq \frac { C } { | z | ^ { 2 n - 2 } }. \end{equation*}

Let $B$ be the space of all forms of type (a6) such that the harmonic function $\overline { u }$ is representable for some $m$ by the Bochner–Martinelli-type integral (cf. also Bochner–Martinelli representation formula)

\begin{equation*} \overline { u } ( z ) = \int _ { \partial D _ { m } } w ( \zeta ) \frac { \sum _ { k = 1 } ^ { n } ( - 1 ) ^ { k - 1 } ( \overline { \zeta } _ { k } - \overline{z} _ { k } ) d \overline { \zeta } [ k ] \wedge d \zeta } { | \zeta - z | ^ { 2 n } }, \end{equation*}

where $z \in \mathbf{C} ^ { n } \backslash \overline { D } _ { m }$ and $\omega ( \zeta ) \in C ( \partial D _ { m } )$. Then one has an isomorphism

\begin{equation*} A ( D ) ^ { * } \simeq A / B; \end{equation*}

it is defined by the formula

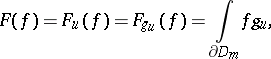(a7)

where $f \in A ( D )$ and $g _ { u } \in A / B$. Note that (a7) gives a more concrete description of the duality than does (a5). The integral in (a7) is also independent of the choice of $m$.

Other descriptions of the spaces dual to spaces of holomorphic functions for special classes of domains can be found in [a18], [a19], [a20], [a21], [a22], [a23], [a24], [a10].

References

[a1]	A. Grothendieck, "Sur certain espaces de fonctions holomorphes" J. Reine Angew. Math. , 192 (1953) pp. 35–64; 77–95 MR0062335 MR0058865
[a2]	G. Köthe, "Dualität in der Funktionentheorie" J. Reine Angew. Math. , 191 (1953) pp. 30–39 MR0056824 Zbl 0050.33502
[a3]	J. Sebastião e Silva, "Analytic functions in functional analysis" Portug. Math. , 9 (1950) pp. 1–130
[a4]	A. Martineau, "Sur la topologies des espaces de fonctions holomorphes" Math. Ann. , 163 (1966) pp. 62–88 MR190697
[a5]	L. Aizenberg, "The general form of a linear continuous functional in spaces of functions holomorphic in convex domains in $\mathbf{C} ^ { n }$" Soviet Math. Dokl. , 7 (1966) pp. 198–202
[a6]	L. Aizenberg, "Linear convexity in $\mathbf{C} ^ { n }$ and the distributions of the singularities of holomorphic functions" Bull. Acad. Polon. Sci. Ser. Math. Astr. Phiz. , 15 (1967) pp. 487–495 (In Russian) MR0222346
[a7]	S.V. Zhamenskij, "A geometric criterion of strong linear convexity" Funct. Anal. Appl. , 13 (1979) pp. 224–225
[a8]	M. Andersson, "Cauchy–Fantappié–Leray formulas with local sections and the inverse Fantappié transform" Bull. Soc. Math. France , 120 (1992) pp. 113–128 Zbl 0757.32008
[a9]	S.G. Gindikin, G.M. Henkin, "Integral geometry for $\overline { \partial }$-cohomologies in $q$-linearly concave domains in $\mathbf{CP} ^ { n }$" Funct. Anal. Appl. , 12 (1978) pp. 6–23
[a10]	S.V. Znamenskij, "Strong linear convexity. I: Duality of spaces of holomorphic functions" Sib. Math. J. , 26 (1985) pp. 331–341 Zbl 0596.32017
[a11]	S.V. Znamenskij, "Strong linear convexity. II: Existence of holomorphic solutions of linear systems of equations" Sib. Math. J. , 29 (1988) pp. 911–925 Zbl 0689.47004 Zbl 0672.47009
[a12]	L. Aizenberg, S.G. Gindikin, "The general form of a linear continuous functional in spaces of holomorphic functions" Moskov. Oblast. Ped. Just. Uchen. Zap. , 87 (1964) pp. 7–15 (In Russian) MR0180699
[a13]	E.L. Stout, "Harmonic duality, hyperfunctions and removable singularities" Izv. Akad. Nauk Ser. Mat. , 59 (1995) pp. 133–170 MR1481618 Zbl 0876.32003
[a14]	M. Nacinovich, A. Shlapunov, N. Tarkhanov, "Duality in the spaces of solutions of elliptic systems" Ann. Scuola Norm. Sup. Pisa , 26 (1998) pp. 207–232 MR1631573 Zbl 0919.35040
[a15]	J.P. Serre, "Une théorème de dualité" Comment. Math. Helvetici , 29 (1955) pp. 9–26
[a16]	A. Martineau, "Sur les fonctionelles analytiques et la transformation de Fourier–Borel" J. Anal. Math. , 9 (1963) pp. 1–164
[a17]	L. Aizenberg, "Duality in complex analysis" , Israel Math. Conf. Proc. , 11 (1997) pp. 27–35 MR1476701 Zbl 0907.46018
[a18]	H.G. Tillman, "Randverteilungen analytischer funktionen und distributionen" Math. Z. , 59 (1953) pp. 61–83 Zbl 0051.08901
[a19]	S. Rolewicz, "On spaces of holomorphic function" Studia Math. , 21 (1962) pp. 135–160 MR0154146
[a20]	L. Aizenberg, B.S. Mityagin, "The spaces of functions analytic in multi-circular domains" Sib. Mat. Zh. , 1 (1960) pp. 153–170 (In Russian) MR124526
[a21]	L. Aizenberg, "The spaces of functions analytic in $( p , q )$-circular domains" Soviet Math. Dokl. , 2 (1961) pp. 75–82
[a22]	L.J. Ronkin, "On general form of functionals in space of functions, analytic in semicircular domain" Soviet Math. Dokl. , 2 (1961) pp. 673–686 MR131577
[a23]	S.G. Gindikin, "Analytic functions in tubular domains" Soviet Math. Dokl. , 3 (1962)
[a24]	S.D. Simonzhenkov, "Description of the conjugate space of functions that are holomorphic in the domain of a special type" Sib. Math. J. , 22 (1981) MR610784