|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
| − | A free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922701.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922702.png" /> associated to a [[P-divisible group|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922703.png" />-divisible group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922704.png" /> defined over a complete discrete valuation ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922705.png" /> of characteristic 0 with residue field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922706.png" /> of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922707.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922708.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t0922709.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227010.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227011.png" /> is the algebraic closure of the quotient field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227012.png" /> of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227013.png" />; the limit is taken with respect to the mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227014.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227015.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227016.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227017.png" /> is the height of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227019.png" /> has the natural structure of a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227020.png" />-module. The functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227021.png" /> allows one to reduce a number of questions about the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227022.png" /> to simpler questions about <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227023.png" />-modules.
| + | <!-- |
| | + | t0922701.png |
| | + | $#A+1 = 60 n = 4 |
| | + | $#C+1 = 60 : ~/encyclopedia/old_files/data/T092/T.0902270 Tate module |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | The Tate module is defined similarly for an [[Abelian variety|Abelian variety]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227024.png" /> be an Abelian variety defined over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227025.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227026.png" /> be the group of points of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227027.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227028.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227029.png" /> is defined as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227030.png" />. The Tate module of a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227031.png" /> is the Tate module of its [[Jacobi variety|Jacobi variety]].
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | The construction of the module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227032.png" /> can be extended to number fields. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227033.png" /> be an algebraic number field and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227034.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227035.png" />-extension of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227036.png" /> (an extension with Galois group isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227037.png" />). For the intermediate field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227038.png" /> of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227039.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227040.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227041.png" /> be the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227042.png" />-component of the ideal class group of the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227043.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227044.png" />, where the limit is taken with respect to norm-mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227045.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227046.png" />. The module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227047.png" /> is characterized by its Iwasawa invariants <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227048.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227050.png" />, defined by
| + | A free $ \mathbf Z _ {p} $- |
| | + | module $ T ( G) $ |
| | + | associated to a [[P-divisible group| $ p $- |
| | + | divisible group]] $ G $ |
| | + | defined over a complete discrete valuation ring $ R $ |
| | + | of characteristic 0 with residue field $ k $ |
| | + | of characteristic $ p $. |
| | + | Let $ G = \{ G _ \nu , i _ \nu \} $, |
| | + | $ \nu \geq 0 $, |
| | + | and $ T ( G) = \lim\limits _ \leftarrow G _ \nu ( \overline{K}\; ) $, |
| | + | where $ \overline{K}\; $ |
| | + | is the algebraic closure of the quotient field $ K $ |
| | + | of the ring $ R $; |
| | + | the limit is taken with respect to the mappings $ j _ \nu : G _ {\nu + 1 } \rightarrow G _ \nu $ |
| | + | for which $ i _ \nu \circ j _ \nu = p $. |
| | + | Then $ T ( G) = \mathbf Z _ {p} ^ {h} $, |
| | + | where $ h $ |
| | + | is the height of the group $ G $ |
| | + | and $ T ( G) $ |
| | + | has the natural structure of a $ G ( \overline{K}\; /K) $- |
| | + | module. The functor $ G \rightarrow T ( G) $ |
| | + | allows one to reduce a number of questions about the group $ G $ |
| | + | to simpler questions about $ G ( \overline{K}\; /K) $- |
| | + | modules. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227051.png" /></td> </tr></table>
| + | The Tate module is defined similarly for an [[Abelian variety|Abelian variety]]. Let $ A $ |
| | + | be an Abelian variety defined over $ k $, |
| | + | and let $ A _ {p ^ {n} } $ |
| | + | be the group of points of order $ p ^ {n} $ |
| | + | in $ A ( \overline{k}\; ) $. |
| | + | Then $ T ( A) $ |
| | + | is defined as $ \lim\limits _ \leftarrow A _ {p ^ {n} } $. |
| | + | The Tate module of a curve $ X $ |
| | + | is the Tate module of its [[Jacobi variety|Jacobi variety]]. |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227052.png" /> for all sufficiently large <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227053.png" />. For cyclotomic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227054.png" />-extensions the invariant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227055.png" /> is equal to 0. This was also proved for Abelian fields [[#References|[4]]]. Examples are known of non-cyclotomic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227056.png" />-extensions with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227057.png" /> (see [[#References|[3]]]). Even in the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227059.png" /> is not necessarily a free <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227060.png" />-module.
| + | The construction of the module $ T _ {p} ( X) $ |
| | + | can be extended to number fields. Let $ K $ |
| | + | be an algebraic number field and let $ k _ \infty $ |
| | + | be a $ \mathbf Z _ {p} $- |
| | + | extension of the field $ k $( |
| | + | an extension with Galois group isomorphic to $ \mathbf Z _ {p} $). |
| | + | For the intermediate field $ k _ {n} $ |
| | + | of degree $ p ^ {n} $ |
| | + | over $ k $, |
| | + | let $ \mathop{\rm Cl} ( k _ {n} ) _ {p} $ |
| | + | be the $ p $- |
| | + | component of the ideal class group of the field $ k _ {n} $. |
| | + | Then $ T _ {p} ( k _ \infty ) = \lim\limits _ \leftarrow \mathop{\rm Cl} ( k _ {n} ) _ {p} $, |
| | + | where the limit is taken with respect to norm-mappings $ \mathop{\rm Cl} ( k _ {m} ) _ {p} \rightarrow \mathop{\rm Cl} ( k _ {n} ) _ {p} $ |
| | + | for $ m > n $. |
| | + | The module $ T _ {p} ( k _ \infty ) $ |
| | + | is characterized by its Iwasawa invariants $ \lambda $, |
| | + | $ \mu $ |
| | + | and $ \nu $, |
| | + | defined by |
| | + | |
| | + | $$ |
| | + | | \mathop{\rm Cl} ( k _ {n} ) _ {p} | = \ |
| | + | p ^ {e _ {n} } , |
| | + | $$ |
| | + | |
| | + | where $ e _ {n} = \lambda n + \mu p ^ {n + \nu } $ |
| | + | for all sufficiently large $ n $. |
| | + | For cyclotomic $ \mathbf Z _ {p} $- |
| | + | extensions the invariant $ \mu $ |
| | + | is equal to 0. This was also proved for Abelian fields [[#References|[4]]]. Examples are known of non-cyclotomic $ \mathbf Z _ {p} $- |
| | + | extensions with $ \mu > 0 $( |
| | + | see [[#References|[3]]]). Even in the case when $ \mu = 0 $, |
| | + | $ T _ {p} ( k _ \infty ) $ |
| | + | is not necessarily a free $ \mathbf Z _ {p} $- |
| | + | module. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.T. Tate, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227061.png" />-divisible groups" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 158–183</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> K. Iwasawa, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227062.png" />-invariants of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227063.png" />-extensions" , ''Number theory, algebraic geometry and commutative algebra'' , Kinokuniya (1973) pp. 1–11</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Ferrero, L.C. Washington, "The Iwasawa invariant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227064.png" /> vanishes for abelian number fields" ''Ann. of Math.'' , '''109''' (1979) pp. 377–395</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.T. Tate, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227061.png" />-divisible groups" T.A. Springer (ed.) et al. (ed.) , ''Proc. Conf. local fields (Driebergen, 1966)'' , Springer (1967) pp. 158–183 {{MR|0231827}} {{ZBL|0157.27601}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> K. Iwasawa, "On the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227062.png" />-invariants of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227063.png" />-extensions" , ''Number theory, algebraic geometry and commutative algebra'' , Kinokuniya (1973) pp. 1–11 {{MR|357371}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Ferrero, L.C. Washington, "The Iwasawa invariant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092270/t09227064.png" /> vanishes for abelian number fields" ''Ann. of Math.'' , '''109''' (1979) pp. 377–395 {{MR|528968}} {{ZBL|0443.12001}} </TD></TR></table> |
A free $ \mathbf Z _ {p} $-
module $ T ( G) $
associated to a $ p $-
divisible group $ G $
defined over a complete discrete valuation ring $ R $
of characteristic 0 with residue field $ k $
of characteristic $ p $.
Let $ G = \{ G _ \nu , i _ \nu \} $,
$ \nu \geq 0 $,
and $ T ( G) = \lim\limits _ \leftarrow G _ \nu ( \overline{K}\; ) $,
where $ \overline{K}\; $
is the algebraic closure of the quotient field $ K $
of the ring $ R $;
the limit is taken with respect to the mappings $ j _ \nu : G _ {\nu + 1 } \rightarrow G _ \nu $
for which $ i _ \nu \circ j _ \nu = p $.
Then $ T ( G) = \mathbf Z _ {p} ^ {h} $,
where $ h $
is the height of the group $ G $
and $ T ( G) $
has the natural structure of a $ G ( \overline{K}\; /K) $-
module. The functor $ G \rightarrow T ( G) $
allows one to reduce a number of questions about the group $ G $
to simpler questions about $ G ( \overline{K}\; /K) $-
modules.
The Tate module is defined similarly for an Abelian variety. Let $ A $
be an Abelian variety defined over $ k $,
and let $ A _ {p ^ {n} } $
be the group of points of order $ p ^ {n} $
in $ A ( \overline{k}\; ) $.
Then $ T ( A) $
is defined as $ \lim\limits _ \leftarrow A _ {p ^ {n} } $.
The Tate module of a curve $ X $
is the Tate module of its Jacobi variety.
The construction of the module $ T _ {p} ( X) $
can be extended to number fields. Let $ K $
be an algebraic number field and let $ k _ \infty $
be a $ \mathbf Z _ {p} $-
extension of the field $ k $(
an extension with Galois group isomorphic to $ \mathbf Z _ {p} $).
For the intermediate field $ k _ {n} $
of degree $ p ^ {n} $
over $ k $,
let $ \mathop{\rm Cl} ( k _ {n} ) _ {p} $
be the $ p $-
component of the ideal class group of the field $ k _ {n} $.
Then $ T _ {p} ( k _ \infty ) = \lim\limits _ \leftarrow \mathop{\rm Cl} ( k _ {n} ) _ {p} $,
where the limit is taken with respect to norm-mappings $ \mathop{\rm Cl} ( k _ {m} ) _ {p} \rightarrow \mathop{\rm Cl} ( k _ {n} ) _ {p} $
for $ m > n $.
The module $ T _ {p} ( k _ \infty ) $
is characterized by its Iwasawa invariants $ \lambda $,
$ \mu $
and $ \nu $,
defined by
$$
| \mathop{\rm Cl} ( k _ {n} ) _ {p} | = \
p ^ {e _ {n} } ,
$$
where $ e _ {n} = \lambda n + \mu p ^ {n + \nu } $
for all sufficiently large $ n $.
For cyclotomic $ \mathbf Z _ {p} $-
extensions the invariant $ \mu $
is equal to 0. This was also proved for Abelian fields [4]. Examples are known of non-cyclotomic $ \mathbf Z _ {p} $-
extensions with $ \mu > 0 $(
see [3]). Even in the case when $ \mu = 0 $,
$ T _ {p} ( k _ \infty ) $
is not necessarily a free $ \mathbf Z _ {p} $-
module.
References
| [1] | J.T. Tate, "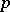 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 |
| [2] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
| [3] | K. Iwasawa, "On the 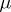 -invariants of -invariants of 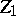 -extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371 -extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371 |
| [4] | B. Ferrero, L.C. Washington, "The Iwasawa invariant 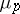 vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001 |
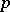 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601
-divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 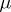 -invariants of
-invariants of 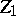 -extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371
-extensions" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 1–11 MR357371 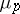 vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001
vanishes for abelian number fields" Ann. of Math. , 109 (1979) pp. 377–395 MR528968 Zbl 0443.12001