Difference between revisions of "Solvable flow"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A flow on a [[Solv manifold|solv manifold]] | + | <!-- |
| + | s0861201.png | ||
| + | $#A+1 = 19 n = 3 | ||
| + | $#C+1 = 19 : ~/encyclopedia/old_files/data/S086/S.0806120 Solvable flow | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A flow on a [[Solv manifold|solv manifold]] $ M = G/H $ | ||
| + | determined by the action on $ M $ | ||
| + | of some one-parameter subgroup $ g _ {t} $ | ||
| + | of the solvable Lie group $ G $: | ||
| + | If $ M $ | ||
| + | consists of the cosets $ gH $, | ||
| + | then under the action of the solvable flow such a coset goes to the coset $ g _ {t} gH $ | ||
| + | at time $ t $. | ||
| + | A particular case of a solvable flow is a [[Nil flow|nil-flow]]; in the general case the properties of a solvable flow can be considerably more diverse. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Auslander, L. Green, F. Hahn, "Flows on homogeneous spaces" , Princeton Univ. Press (1963)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.M. Stepin, "Flows on solvmanifolds" ''Uspekhi Mat. Nauk'' , '''24''' : 5 (1969) pp. 241 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L. Auslander, "An exposition of the structure of solvmanifolds. Part II: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086120/s0861209.png" />-induced flows" ''Bull. Amer. Math. Soc.'' , '''79''' : 2 (1973) pp. 262–285</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Safonov, "Spectral type of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086120/s08612010.png" />-induced ergodic flows" ''Functional Anal. Appl.'' , '''14''' : 4 (1980) pp. 315–317 ''Funkts. Anal. i Prilozhen.'' , '''14''' : 4 (1980) pp. 81–82</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Auslander, L. Green, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086120/s08612011.png" />-induced flows and solvmanifolds" ''Amer. J. Math.'' , '''88''' (1966) pp. 43–60</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L. Auslander, L. Green, F. Hahn, "Flows on homogeneous spaces" , Princeton Univ. Press (1963)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.M. Stepin, "Flows on solvmanifolds" ''Uspekhi Mat. Nauk'' , '''24''' : 5 (1969) pp. 241 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L. Auslander, "An exposition of the structure of solvmanifolds. Part II: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086120/s0861209.png" />-induced flows" ''Bull. Amer. Math. Soc.'' , '''79''' : 2 (1973) pp. 262–285</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Safonov, "Spectral type of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086120/s08612010.png" />-induced ergodic flows" ''Functional Anal. Appl.'' , '''14''' : 4 (1980) pp. 315–317 ''Funkts. Anal. i Prilozhen.'' , '''14''' : 4 (1980) pp. 81–82</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> L. Auslander, L. Green, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086120/s08612011.png" />-induced flows and solvmanifolds" ''Amer. J. Math.'' , '''88''' (1966) pp. 43–60</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | In many cases dynamical properties of the flow, such as [[Ergodicity|ergodicity]], can be deduced from algebraic properties of | + | In many cases dynamical properties of the flow, such as [[Ergodicity|ergodicity]], can be deduced from algebraic properties of $ G $ |
| + | and $ H $. | ||
| + | The [[Kronecker theorem|Kronecker theorem]] implies ergodicity for the case $ G = \mathbf R ^ {n} $, | ||
| + | $ H = \mathbf Z ^ {n} $, | ||
| + | the integer lattice, and the flow (written additively) given by $ g _ {t} ( x + \mathbf Z ^ {n} ) = x + t a + \mathbf Z ^ {n} $, | ||
| + | where $ x + \mathbf Z ^ {n} $ | ||
| + | is a coset of $ \mathbf R ^ {n} / \mathbf Z ^ {n} $ | ||
| + | and $ a \in \mathbf R ^ {n} $ | ||
| + | is a fixed vector whose components are linearly independent over the rational numbers. When $ G= \mathop{\rm SL} ( 2, \mathbf R ) $ | ||
| + | and $ H $ | ||
| + | is a discrete subgroup, certain one-parameter subgroups of $ G $ | ||
| + | correspond to geodesic and horocycle flow (cf. [[Geodesic flow|Geodesic flow]]; [[Horocycle flow|Horocycle flow]]) on unit tangent bundles of surfaces of constant negative curvature (cf. [[Constant curvature, space of|Constant curvature, space of]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Brezin, C.C. Moore, "Flows on homogeneous spaces" ''Amer. J. Math.'' , '''103''' (1981) pp. 571–613</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Brezin, C.C. Moore, "Flows on homogeneous spaces" ''Amer. J. Math.'' , '''103''' (1981) pp. 571–613</TD></TR></table> | ||
Latest revision as of 08:14, 6 June 2020
A flow on a solv manifold $ M = G/H $
determined by the action on $ M $
of some one-parameter subgroup $ g _ {t} $
of the solvable Lie group $ G $:
If $ M $
consists of the cosets $ gH $,
then under the action of the solvable flow such a coset goes to the coset $ g _ {t} gH $
at time $ t $.
A particular case of a solvable flow is a nil-flow; in the general case the properties of a solvable flow can be considerably more diverse.
References
| [1] | L. Auslander, L. Green, F. Hahn, "Flows on homogeneous spaces" , Princeton Univ. Press (1963) |
| [2] | A.M. Stepin, "Flows on solvmanifolds" Uspekhi Mat. Nauk , 24 : 5 (1969) pp. 241 (In Russian) |
| [3] | L. Auslander, "An exposition of the structure of solvmanifolds. Part II: 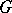 -induced flows" Bull. Amer. Math. Soc. , 79 : 2 (1973) pp. 262–285 -induced flows" Bull. Amer. Math. Soc. , 79 : 2 (1973) pp. 262–285 |
| [4] | A.V. Safonov, "Spectral type of 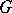 -induced ergodic flows" Functional Anal. Appl. , 14 : 4 (1980) pp. 315–317 Funkts. Anal. i Prilozhen. , 14 : 4 (1980) pp. 81–82 -induced ergodic flows" Functional Anal. Appl. , 14 : 4 (1980) pp. 315–317 Funkts. Anal. i Prilozhen. , 14 : 4 (1980) pp. 81–82 |
| [5] | L. Auslander, L. Green, "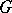 -induced flows and solvmanifolds" Amer. J. Math. , 88 (1966) pp. 43–60 -induced flows and solvmanifolds" Amer. J. Math. , 88 (1966) pp. 43–60 |
Comments
In many cases dynamical properties of the flow, such as ergodicity, can be deduced from algebraic properties of $ G $ and $ H $. The Kronecker theorem implies ergodicity for the case $ G = \mathbf R ^ {n} $, $ H = \mathbf Z ^ {n} $, the integer lattice, and the flow (written additively) given by $ g _ {t} ( x + \mathbf Z ^ {n} ) = x + t a + \mathbf Z ^ {n} $, where $ x + \mathbf Z ^ {n} $ is a coset of $ \mathbf R ^ {n} / \mathbf Z ^ {n} $ and $ a \in \mathbf R ^ {n} $ is a fixed vector whose components are linearly independent over the rational numbers. When $ G= \mathop{\rm SL} ( 2, \mathbf R ) $ and $ H $ is a discrete subgroup, certain one-parameter subgroups of $ G $ correspond to geodesic and horocycle flow (cf. Geodesic flow; Horocycle flow) on unit tangent bundles of surfaces of constant negative curvature (cf. Constant curvature, space of).
References
| [a1] | J. Brezin, C.C. Moore, "Flows on homogeneous spaces" Amer. J. Math. , 103 (1981) pp. 571–613 |
Solvable flow. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Solvable_flow&oldid=14625