Difference between revisions of "Infinite product"
(Importing text file) |
(Comment: On divergence to zero) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
An expression of the form | An expression of the form | ||
| − | + | $$ | |
| − | + | \prod_{k=1}^\infty \left({ 1 + u_k }\right) | |
| − | + | \label{(*)} | |
| − | containing an infinite set of factors, numbers or functions, all of which are non-zero. An infinite product is said to be convergent if there exists a non-zero limit of the sequence of partial products | + | $$ |
| − | + | containing an infinite set of factors, numbers or functions, all of which are non-zero. An infinite product is said to be ''convergent'' if there exists a non-zero limit of the sequence of partial products | |
| − | + | $$ | |
| − | + | P_n = \prod_{k=1}^n \left({ 1 + u_k }\right) | |
| − | as | + | $$ |
| − | + | as $n \rightarrow \infty$. The value of the infinite product is the limit | |
| − | + | $$ | |
| − | + | P = \lim_{n\rightarrow\infty} P_n | |
| + | $$ | ||
and one writes | and one writes | ||
| − | + | $$ | |
| − | + | \prod_{k=1}^\infty \left({ 1 + u_k }\right) = P \ . | |
| + | $$ | ||
An infinite product converges if and only if the series | An infinite product converges if and only if the series | ||
| − | + | $$ | |
| − | + | \sum_{k=1}^\infty \log \left({ 1 + u_k }\right) | |
| − | + | $$ | |
is convergent. Accordingly, the study of the convergence of infinite products is reduced to the study of the convergence of series. The infinite product (*) is said to be absolutely convergent if the infinite product | is convergent. Accordingly, the study of the convergence of infinite products is reduced to the study of the convergence of series. The infinite product (*) is said to be absolutely convergent if the infinite product | ||
| − | + | $$ | |
| − | + | \prod_{k=1}^\infty \left({ 1 + |u_k| }\right) | |
| − | + | $$ | |
is convergent. A necessary and sufficient condition for absolute convergence of the infinite product (*) is absolute convergence of the series | is convergent. A necessary and sufficient condition for absolute convergence of the infinite product (*) is absolute convergence of the series | ||
| − | + | $$ | |
| − | + | \sum_{k=1}^\infty u_k \ . | |
| + | $$ | ||
An infinite product has the rearrangement property (i.e. its value is independent of the order of the factors) if and only if it is absolutely convergent. | An infinite product has the rearrangement property (i.e. its value is independent of the order of the factors) if and only if it is absolutely convergent. | ||
The infinite product (*) with factors which are functions | The infinite product (*) with factors which are functions | ||
| − | + | $$ | |
| − | + | \left({ 1 + u_k }\right) = \left({ 1 + u_k(z) }\right) | |
| − | + | $$ | |
| − | defined, for example, in a domain | + | defined, for example, in a domain $D$ of the complex $z$-plane, converges uniformly in $D$ if the sequence of partial products $P_n(z)$ converges uniformly in $D$ to a non-zero limit. A very important case in practical applications is when certain factors have zeros in $D$ such that at most a finite number of the zeros lie in any compact set $K \subseteq D$. The concept of convergence is generalized as follows: The infinite product (*) is said to be (absolutely, uniformly) convergent inside $D$ if for any compact set $K \subseteq D$ there exists a number $N = N(K)$ such that all the factors $\left({ 1 + u_k(z) }\right) \neq 0$ for $k \ge N$, while the sequence of partial products |
| − | + | $$ | |
| − | + | \prod_{k=N}^n \left({ 1 + u_k(z) }\right) | |
| − | + | $$ | |
| − | converges (absolutely, uniformly) on | + | converges (absolutely, uniformly) on $K$ to a non-zero limit. If all factors are analytic functions in $D$ and if the infinite product converges uniformly inside $D$, its limit is an analytic function in $D$. |
Infinite products were first encountered by F. Viète (1593) in his study of the quadrature of the circle. He represented the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050880/i05088027.png" /> analytically by the following infinite product: | Infinite products were first encountered by F. Viète (1593) in his study of the quadrature of the circle. He represented the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050880/i05088027.png" /> analytically by the following infinite product: | ||
| + | $$ | ||
| + | \frac{2}{\pi} = \sqrt{ \frac{1}{2} } \cdot \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} } } \cdot \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} } } } \cdots \ . | ||
| + | $$ | ||
| − | + | Another representation of $\pi$ is due to J. Wallis (1665): | |
| + | $$ | ||
| + | \frac{4}{\pi} = \frac32 \cdot \frac34 \cdot \frac54 \cdot \frac56 \cdot \frac 76 \cdot \frac78 \cdots \ . | ||
| + | $$ | ||
| − | + | Infinite products with factors that are functions were encountered by L. Euler (1742); an example is | |
| + | $$ | ||
| + | \sin z = z \prod_{k=1}^\infty \left({ 1 - \frac{z^2}{k^2\pi^2} }\right) \ . | ||
| + | $$ | ||
| − | + | Infinite products are a principal tool in representing analytic functions with explicit indication of their zeros; for [[entire function]]s they are the analogue of the factors of polynomials. See also [[Blaschke product]]; [[Weierstrass theorem]] on infinite products; [[Canonical product]]. | |
| − | <table | + | ====References==== |
| + | <table> | ||
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , '''1''' , MIR (1982) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) (In Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1969) (In Russian) {{ZBL|0183.33601}}</TD></TR> | ||
| + | </table> | ||
| − | |||
| − | |||
| − | + | ====Comments==== | |
| + | See also [[Hadamard theorem]] on entire functions. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[ | + | <table> |
| − | + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J.B. Conway, "Functions of one complex variable" , Springer (1984) {{ZBL|0277.30001}}</TD></TR> | |
| − | + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> A.S.B. Holland, "Introduction to the theory of entire functions" , Acad. Press (1973) {{ZBL|0278.30001}}</TD></TR> | |
| + | </table> | ||
====Comments==== | ====Comments==== | ||
| − | + | It should be noted in the definition above that an infinite product is said to converge if the limit of the sequence of partial products $P_n$ is non-zero. If the limit is zero than the product is said to ''diverge to zero''. | |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[ | + | <table> |
| + | <TR><TD valign="top">[b1]</TD> <TD valign="top"> R.A. Rankin, "An Introduction to Mathematical Analysis", Pergamon Press (1963) {{ZBL|0112.28103}}</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|done}} | ||
Latest revision as of 17:20, 24 April 2016
An expression of the form $$ \prod_{k=1}^\infty \left({ 1 + u_k }\right) \label{(*)} $$ containing an infinite set of factors, numbers or functions, all of which are non-zero. An infinite product is said to be convergent if there exists a non-zero limit of the sequence of partial products $$ P_n = \prod_{k=1}^n \left({ 1 + u_k }\right) $$ as $n \rightarrow \infty$. The value of the infinite product is the limit $$ P = \lim_{n\rightarrow\infty} P_n $$ and one writes $$ \prod_{k=1}^\infty \left({ 1 + u_k }\right) = P \ . $$
An infinite product converges if and only if the series $$ \sum_{k=1}^\infty \log \left({ 1 + u_k }\right) $$ is convergent. Accordingly, the study of the convergence of infinite products is reduced to the study of the convergence of series. The infinite product (*) is said to be absolutely convergent if the infinite product $$ \prod_{k=1}^\infty \left({ 1 + |u_k| }\right) $$ is convergent. A necessary and sufficient condition for absolute convergence of the infinite product (*) is absolute convergence of the series $$ \sum_{k=1}^\infty u_k \ . $$
An infinite product has the rearrangement property (i.e. its value is independent of the order of the factors) if and only if it is absolutely convergent.
The infinite product (*) with factors which are functions $$ \left({ 1 + u_k }\right) = \left({ 1 + u_k(z) }\right) $$ defined, for example, in a domain $D$ of the complex $z$-plane, converges uniformly in $D$ if the sequence of partial products $P_n(z)$ converges uniformly in $D$ to a non-zero limit. A very important case in practical applications is when certain factors have zeros in $D$ such that at most a finite number of the zeros lie in any compact set $K \subseteq D$. The concept of convergence is generalized as follows: The infinite product (*) is said to be (absolutely, uniformly) convergent inside $D$ if for any compact set $K \subseteq D$ there exists a number $N = N(K)$ such that all the factors $\left({ 1 + u_k(z) }\right) \neq 0$ for $k \ge N$, while the sequence of partial products $$ \prod_{k=N}^n \left({ 1 + u_k(z) }\right) $$ converges (absolutely, uniformly) on $K$ to a non-zero limit. If all factors are analytic functions in $D$ and if the infinite product converges uniformly inside $D$, its limit is an analytic function in $D$.
Infinite products were first encountered by F. Viète (1593) in his study of the quadrature of the circle. He represented the number 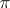 analytically by the following infinite product:
$$
\frac{2}{\pi} = \sqrt{ \frac{1}{2} } \cdot \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} } } \cdot \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} } } } \cdots \ .
$$
analytically by the following infinite product:
$$
\frac{2}{\pi} = \sqrt{ \frac{1}{2} } \cdot \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} } } \cdot \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} + \frac{1}{2} \sqrt{ \frac{1}{2} } } } \cdots \ .
$$
Another representation of $\pi$ is due to J. Wallis (1665): $$ \frac{4}{\pi} = \frac32 \cdot \frac34 \cdot \frac54 \cdot \frac56 \cdot \frac 76 \cdot \frac78 \cdots \ . $$
Infinite products with factors that are functions were encountered by L. Euler (1742); an example is $$ \sin z = z \prod_{k=1}^\infty \left({ 1 - \frac{z^2}{k^2\pi^2} }\right) \ . $$
Infinite products are a principal tool in representing analytic functions with explicit indication of their zeros; for entire functions they are the analogue of the factors of polynomials. See also Blaschke product; Weierstrass theorem on infinite products; Canonical product.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1 , MIR (1982) (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
| [3] | A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1969) (In Russian) Zbl 0183.33601 |
Comments
See also Hadamard theorem on entire functions.
References
| [a1] | J.B. Conway, "Functions of one complex variable" , Springer (1984) Zbl 0277.30001 |
| [a2] | A.S.B. Holland, "Introduction to the theory of entire functions" , Acad. Press (1973) Zbl 0278.30001 |
Comments
It should be noted in the definition above that an infinite product is said to converge if the limit of the sequence of partial products $P_n$ is non-zero. If the limit is zero than the product is said to diverge to zero.
References
| [b1] | R.A. Rankin, "An Introduction to Mathematical Analysis", Pergamon Press (1963) Zbl 0112.28103 |
Infinite product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinite_product&oldid=13531