Difference between revisions of "Folium of Descartes"
(Importing text file) |
(svg image) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | f0407501.png | ||
| + | $#A+1 = 10 n = 0 | ||
| + | $#C+1 = 10 : ~/encyclopedia/old_files/data/F040/F.0400750 Folium of Descartes | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A plane algebraic curve of order three which is given in Cartesian coordinates by the equation $ x ^ {3} + y ^ {3} - 3axy = 0 $; | |
| + | the parametric equations are | ||
| − | + | $$ | |
| + | x = | ||
| + | \frac{3at}{1 + t ^ {3} } | ||
| + | ,\ y = | ||
| + | \frac{3a t ^ {2} }{1 + t ^ {3} } | ||
| + | , | ||
| + | $$ | ||
| − | + | where $ t $ | |
| + | is the tangent of the angle between the radius vector of the curve and the $ x $- | ||
| + | axis. The folium of Descartes is symmetric about the axis $y=x$ (see Fig.). The tangent lines are parallel to the coordinate axes at the points with coordinates $ ( a 2 ^ {1/3} , a 4 ^ {1/3} ) $ | ||
| + | and $ ( a 4 ^ {1/3} , a 2 ^ {1/3} ) $. | ||
| + | The coordinate origin is a nodal point with the coordinate axes as tangent lines. The asymptote is given by $ y= - x- a $. | ||
| + | The surface area enclosed between the curve and the asymptote is $ S = 3a ^ {2} /2 $. | ||
| + | The surface area of the loop is $ S = 3a ^ {2} /2 $. | ||
| − | + | This curve is named after R. Descartes who was the first to study it in 1638. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[File:Folium of Descartes.svg|center|300px|Folium of Descartes (a=1)]] | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)</TD></TR><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962)</TD></TR></table> |
Latest revision as of 16:37, 16 March 2023
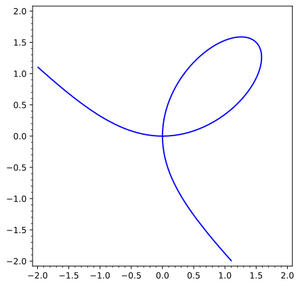
A plane algebraic curve of order three which is given in Cartesian coordinates by the equation $ x ^ {3} + y ^ {3} - 3axy = 0 $;
the parametric equations are
$$ x = \frac{3at}{1 + t ^ {3} } ,\ y = \frac{3a t ^ {2} }{1 + t ^ {3} } , $$
where $ t $ is the tangent of the angle between the radius vector of the curve and the $ x $- axis. The folium of Descartes is symmetric about the axis $y=x$ (see Fig.). The tangent lines are parallel to the coordinate axes at the points with coordinates $ ( a 2 ^ {1/3} , a 4 ^ {1/3} ) $ and $ ( a 4 ^ {1/3} , a 2 ^ {1/3} ) $. The coordinate origin is a nodal point with the coordinate axes as tangent lines. The asymptote is given by $ y= - x- a $. The surface area enclosed between the curve and the asymptote is $ S = 3a ^ {2} /2 $. The surface area of the loop is $ S = 3a ^ {2} /2 $.
This curve is named after R. Descartes who was the first to study it in 1638.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian) |
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
Folium of Descartes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Folium_of_Descartes&oldid=13430