Difference between revisions of "Dodecahedron"
From Encyclopedia of Mathematics
(Importing text file) |
m (OldImage template added) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | One of the five types of [[Regular polyhedra|regular polyhedra]]. A dodecahedron has 12 (pentagonal) faces, 30 edges and 20 vertices (with three edges meeting at each vertex). If | + | {{TEX|done}} |
| + | One of the five types of [[Regular polyhedra|regular polyhedra]]. A dodecahedron has 12 (pentagonal) faces, 30 edges and 20 vertices (with three edges meeting at each vertex). If $a$ is the edge length of a dodecahedron, its volume is | ||
| − | + | $$v=\frac{a^3}{4}(15+7\sqrt5)\approx7.6631a^3.$$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033750a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033750a.gif" /> | ||
Figure: d033750a | Figure: d033750a | ||
| + | |||
| + | {{OldImage}} | ||
Latest revision as of 11:59, 26 March 2023
One of the five types of regular polyhedra. A dodecahedron has 12 (pentagonal) faces, 30 edges and 20 vertices (with three edges meeting at each vertex). If $a$ is the edge length of a dodecahedron, its volume is
$$v=\frac{a^3}{4}(15+7\sqrt5)\approx7.6631a^3.$$
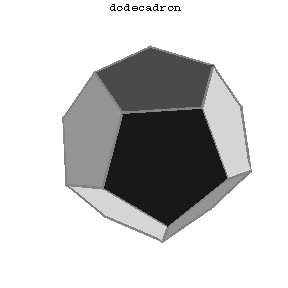
Figure: d033750a
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Dodecahedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dodecahedron&oldid=13229
Dodecahedron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dodecahedron&oldid=13229
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article