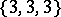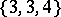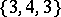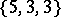Regular polyhedra
Platonic solids
Convex polyhedra such that all faces are congruent regular polygons and such that all polyhedral angles at the vertices are regular and equal (Fig.1a–Fig.1e).
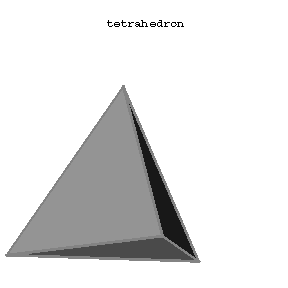
Figure: r080790a
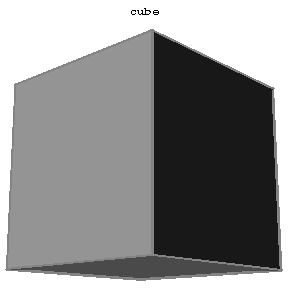
Figure: r080790b

Figure: r080790c
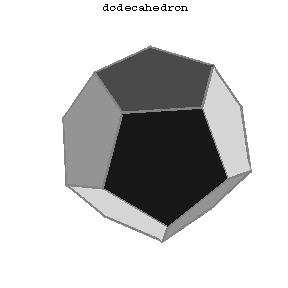
Figure: r080790d

Figure: r080790e
In the Euclidean space  there are five regular polyhedra, the data of which are given in Table 1, where the Schläfli symbol
there are five regular polyhedra, the data of which are given in Table 1, where the Schläfli symbol 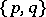 (cf. Polyhedron group) denotes the regular polyhedron with
(cf. Polyhedron group) denotes the regular polyhedron with 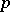 -gonal faces and
-gonal faces and 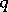 -hedral angles'
-hedral angles'
<tbody> </tbody>
|
Dual polyhedra, or reciprocal polyhedra, 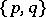 and
and 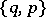 are, by definition, those which transform into each other upon reciprocation with respect to any concentric sphere. The tetrahedron is dual to itself, the hexahedron to the octahedron and the dodecahedron to the icosahedron.
are, by definition, those which transform into each other upon reciprocation with respect to any concentric sphere. The tetrahedron is dual to itself, the hexahedron to the octahedron and the dodecahedron to the icosahedron.
Polyhedra in spaces of more than three dimensions are called polytopes.
In 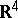 there are six regular polytopes, the data of which are given in Table 2.'
there are six regular polytopes, the data of which are given in Table 2.'
<tbody> </tbody>
|
In  ,
, 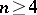 , there are three regular polytopes: the analogues of the tetrahedron, the cube and the octahedron; their Schläfli symbols are:
, there are three regular polytopes: the analogues of the tetrahedron, the cube and the octahedron; their Schläfli symbols are: 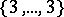 ,
, 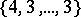 and
and 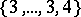 .
.
If one permits self-intersection, then there are 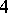 more regular polyhedra, namely the Kepler–Poinsot solids or regular star polyhedra. In these polyhedra, either the faces intersect each other or the faces are self-intersecting polygons (Fig.2a–Fig.2d). The data of these solids are listed in Table 3.
more regular polyhedra, namely the Kepler–Poinsot solids or regular star polyhedra. In these polyhedra, either the faces intersect each other or the faces are self-intersecting polygons (Fig.2a–Fig.2d). The data of these solids are listed in Table 3.

Figure: r080790f

Figure: r080790g

Figure: r080790h
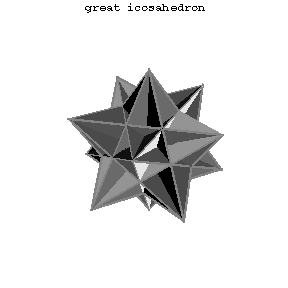
Figure: r080790i
'
<tbody> </tbody>
|
References
| [1] | P.S. Alexandroff [P.S. Aleksandrov] (ed.) et al. (ed.) , Enzyklopaedie der Elementarmathematik , 4. Geometrie , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [2] | L.A. Lyusternik, "Convex figures and polyhedra" , Moscow (1956) (In Russian) |
| [3] | D.O. Shklyarskii, N.N. Chentsov, I.M. Yaglom, "The USSR Olympiad book: selected problems and theorems of elementary mathematics" , Freeman (1962) (Translated from Russian) |
| [4] | H.S.M. Coxeter, "Regular complex polytopes" , Cambridge Univ. Press (1990) |
Comments
At least 2 of the 4 Kepler–Poinsot solids were discovered long before Kepler and Poinsot's times: The small stellated dodecahedron by P. Uccello (around 1420) and the great dodecahedron in 1958 by W. Jamnitzer (cf. [a2], [a3]).
References
| [a1] | B. Grünbaum, "Regular polyhedra - old and new" Aequat. Math. , 16 (1970) pp. 1–20 |
| [a2] | G. Flede (ed.) , Shaping space , Birkhäuser (1988) |
| [a3] | L. Saffaro, "Dai cinqui poliedri platonici all'infinito" Encicl. Sci. e Tecn. Mondadori , 76 (1976) pp. 474–484 |
| [a4] | L. Fejes Toth, "Regular figures" , Pergamon (1964) (Translated from German) |
Regular polyhedra. A.B. Ivanov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_polyhedra&oldid=18524
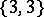
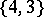
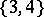
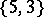
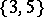
 -dim. faces
-dim. faces -dim. faces
-dim. faces