Difference between revisions of "Reductive space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | r0804501.png | ||
| + | $#A+1 = 117 n = 1 | ||
| + | $#C+1 = 117 : ~/encyclopedia/old_files/data/R080/R.0800450 Reductive space | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Homogeneous space|homogeneous space]] $ G/H $ | |
| + | of a connected [[Lie group|Lie group]] $ G $ | ||
| + | such that in the [[Lie algebra|Lie algebra]] $ \mathfrak g $ | ||
| + | of $ G $ | ||
| + | there is an $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant subspace complementary to the subalgebra $ \mathfrak h \subset \mathfrak g $, | ||
| + | where $ \mathfrak h $ | ||
| + | is the Lie algebra of the group $ H $. | ||
| + | The validity of any of the following conditions is sufficient for the homogeneous space $ G/H $ | ||
| + | to be reductive: 1) the linear group $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $ | ||
| + | is completely reducible; or 2) in $ \mathfrak g $ | ||
| + | there is an $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant bilinear form whose restriction to $ \mathfrak h $ | ||
| + | is non-degenerate. In particular, any homogeneous Riemannian space is reductive. If $ M = G/H $ | ||
| + | is a reductive space and the group $ G $ | ||
| + | acts effectively on $ M $, | ||
| + | then the linear representation of the isotropy group $ H $ | ||
| + | in the tangent space $ M _ {0} $ | ||
| + | to the manifold $ M $ | ||
| + | at the point $ 0 = eH \in M $ | ||
| + | is faithful (cf. [[Faithful representation|Faithful representation]]). Two important $ G $- | ||
| + | invariant affine connections on $ M $ | ||
| + | are associated with each $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant subspace $ \mathfrak m \subset \mathfrak g $ | ||
| + | complementary to $ \mathfrak h $: | ||
| + | the canonical connection and the natural torsion-free connection. The canonical connection on the reductive space $ M = G/H $ | ||
| + | with a fixed $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $ | ||
| + | is the unique $ G $- | ||
| + | invariant affine connection on $ M $ | ||
| + | such that for any vector $ X \in \mathfrak m $ | ||
| + | and any frame $ u $ | ||
| + | at the point 0, the curve $ ( \mathop{\rm exp} tX) u $ | ||
| + | in the principal fibration of frames over $ M $ | ||
| + | is horizontal. The canonical connection is complete and the set of its geodesics through 0 coincides with the set of curves of the type $ ( \mathop{\rm exp} tX) 0 $, | ||
| + | where $ X \in \mathfrak m $. | ||
| + | After the natural identification of the spaces $ \mathfrak m $ | ||
| + | and $ M _ {0} $, | ||
| + | the curvature tensor $ R $ | ||
| + | and torsion tensor $ T $ | ||
| + | of the canonical connection are defined by the formulas $ ( R( X, Y) Z) _ {0} = - [[ X, Y] _ {\mathfrak h} , Z] $ | ||
| + | and $ T( X, Y) _ {0} = -[ X, Y] _ {\mathfrak m} $, | ||
| + | where $ X, Y, Z \in \mathfrak m $ | ||
| + | and $ W _ {\mathfrak h} $ | ||
| + | and $ W _ {\mathfrak m} $ | ||
| + | denote the projections of the vector $ W \in \mathfrak g $ | ||
| + | onto $ \mathfrak h $ | ||
| + | and $ \mathfrak m $, | ||
| + | respectively. | ||
| − | + | The tensor fields $ R $ | |
| + | and $ T $ | ||
| + | are parallel relative to the canonical connection, as is any other $ G $- | ||
| + | invariant tensor field on $ M $. | ||
| + | The Lie algebra of the linear holonomy group (see [[Holonomy group|Holonomy group]]) of the canonical connections on $ M $ | ||
| + | with supporting point 0 is generated by the set $ \{ {\lambda ([ X, Y] _ {\mathfrak h} ) } : {X, Y \in \mathfrak m } \} $, | ||
| + | where $ \lambda $ | ||
| + | is the linear representation of the isotropy Lie algebra $ \mathfrak h $ | ||
| + | in the space $ M _ {0} $. | ||
| + | Any connected simply-connected manifold with a complete affine connection with parallel curvature and torsion fields can be represented as a reductive space whose canonical connection coincides with the given affine connection. In the reductive space $ M = G/H $ | ||
| + | with fixed $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $ | ||
| + | there is a unique $ G $- | ||
| + | invariant affine connection with zero torsion having the same geodesics as the canonical connection. This connection is called the natural torsion-free connection on $ M $( | ||
| + | relative to the decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $). | ||
| + | A homogeneous Riemannian or pseudo-Riemannian space $ M = G/H $ | ||
| + | is naturally reductive if it admits an $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $ | ||
| + | such that | ||
| − | + | $$ \tag{* } | |
| + | B( X, [ Z, Y] _ {\mathfrak m} ) + B ([ Z, X] _ {\mathfrak m} , Y) = 0 | ||
| + | $$ | ||
| − | In addition to reductive spaces, partially reductive spaces are also examined, i.e. homogeneous spaces | + | for all $ X, Y, Z \in \mathfrak m $, |
| + | where $ B $ | ||
| + | is the non-degenerate symmetric bilinear form on $ \mathfrak m $ | ||
| + | induced by the Riemannian (pseudo-Riemannian) structure on $ M $ | ||
| + | under the natural identification of the spaces $ \mathfrak m $ | ||
| + | and $ M _ {0} $. | ||
| + | If $ M = G/H $ | ||
| + | is a naturally reductive Riemannian or pseudo-Riemannian space with a fixed $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $ | ||
| + | that satisfies condition (*), then the natural torsion-free connection coincides with the corresponding Riemannian or pseudo-Riemannian connection on $ M $. | ||
| + | If $ M $ | ||
| + | is a simply-connected naturally reductive homogeneous Riemannian space and $ M = M _ {0} \times \dots \times M _ {r} $ | ||
| + | is its de Rham decomposition, then $ M $ | ||
| + | can be represented in the form $ M = G/H $; | ||
| + | moreover, $ G = G _ {0} \times \dots \times G _ {r} $, | ||
| + | $ H = H _ {0} \times \dots \times H _ {r} $ | ||
| + | and $ M _ {i} = G _ {i} /H _ {i} $ | ||
| + | $ ( i = 0 \dots r) $. | ||
| + | |||
| + | An important generalization of reductive spaces are $ \nu $- | ||
| + | reductive homogeneous spaces [[#References|[4]]]. A homogeneous space $ G/H $ | ||
| + | is called $ \nu $- | ||
| + | reductive if its stationary subalgebra $ \mathfrak h $ | ||
| + | equals $ \mathfrak h _ {1} \dot{+} \dots \dot{+} \mathfrak h _ \nu $, | ||
| + | where $ \mathfrak h _ \nu \neq \{ 0 \} $, | ||
| + | and if there is a subspace $ \mathfrak m $ | ||
| + | in $ \mathfrak h $ | ||
| + | complementary to $ \mathfrak h $ | ||
| + | such that $ [ \mathfrak h _ {i} , \mathfrak m ] \subset \mathfrak h _ {i-} 1 $, | ||
| + | $ i = 1 \dots \nu $, | ||
| + | where $ \mathfrak h _ {0} = \mathfrak m $. | ||
| + | The $ 1 $- | ||
| + | reductive homogeneous spaces are in fact reductive spaces; examples of $ 2 $- | ||
| + | reductive homogeneous spaces are projective (and conformal) spaces on which a group of projective (or conformal) transformations acts. If $ M = G/H $ | ||
| + | there is a $ \nu $- | ||
| + | reductive homogeneous space and if $ \nu > 1 $, | ||
| + | then the linear representation of the isotropy Lie algebra $ \mathfrak h $ | ||
| + | is not faithful (since $ [ \mathfrak h _ {i} , \mathfrak m ] \subset \mathfrak h $ | ||
| + | when $ i > 1 $); | ||
| + | consequently, there is no $ G $- | ||
| + | invariant affine connection on $ M $. | ||
| + | However, there is a canonical $ G $- | ||
| + | invariant connection on a $ \nu $- | ||
| + | reductive homogeneous space with the homogeneous space of some transitive-differential group of order $ \nu $ | ||
| + | as fibre (see [[#References|[4]]]). Reductive and $ \nu $- | ||
| + | reductive spaces are characterized as maximally homogeneous $ G $- | ||
| + | structures (cf. [[G-structure| $ G $- | ||
| + | structure]]) of appropriate type (cf. [[#References|[6]]]). | ||
| + | |||
| + | In addition to reductive spaces, partially reductive spaces are also examined, i.e. homogeneous spaces $ G/H $ | ||
| + | such that there is a decomposition of the Lie algebra $ \mathfrak g $ | ||
| + | into a direct sum of two non-zero $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- | ||
| + | invariant subspaces, one of which contains the subalgebra $ \mathfrak h $( | ||
| + | see [[#References|[5]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''2''' , Interscience (1969)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.K. Rashevskii, "On the geometry of homogeneous spaces" ''Trudy Sem. Vektor. i Tenzor. Anal.'' , '''9''' (1952) pp. 49–74</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> K. Nomizu, "Invariant affine connections on homogeneous spaces" ''Amer. J. Math.'' , '''76''' : 1 (1954) pp. 33–65</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.L. Kantor, "Transitive differential groups and invariant connections in homogeneous spaces" ''Trudy Sem. Vektor. i Tenzor. Anal.'' , '''13''' (1966) pp. 310–398</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.B. Vinberg, "Invariant linear connections in a homogeneous space" ''Trudy Moskov. Mat. Obshch.'' , '''9''' (1960) pp. 191–210 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> D.V. Alekseevskii, "Maximally homogeneous <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080450/r080450119.png" />-structures and filtered Lie algebras" ''Soviet Math. Dokl.'' , '''37''' : 2 (1988) pp. 381–384 ''Dokl. Akad. Nauk SSSR'' , '''299''' : 3 (1988) pp. 521–526</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''2''' , Interscience (1969)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.K. Rashevskii, "On the geometry of homogeneous spaces" ''Trudy Sem. Vektor. i Tenzor. Anal.'' , '''9''' (1952) pp. 49–74</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> K. Nomizu, "Invariant affine connections on homogeneous spaces" ''Amer. J. Math.'' , '''76''' : 1 (1954) pp. 33–65</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> I.L. Kantor, "Transitive differential groups and invariant connections in homogeneous spaces" ''Trudy Sem. Vektor. i Tenzor. Anal.'' , '''13''' (1966) pp. 310–398</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.B. Vinberg, "Invariant linear connections in a homogeneous space" ''Trudy Moskov. Mat. Obshch.'' , '''9''' (1960) pp. 191–210 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> D.V. Alekseevskii, "Maximally homogeneous <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080450/r080450119.png" />-structures and filtered Lie algebras" ''Soviet Math. Dokl.'' , '''37''' : 2 (1988) pp. 381–384 ''Dokl. Akad. Nauk SSSR'' , '''299''' : 3 (1988) pp. 521–526</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , McGraw-Hill (1967)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.A. Wolf, "Spaces of constant curvature" , McGraw-Hill (1967)</TD></TR></table> | ||
Latest revision as of 08:10, 6 June 2020
A homogeneous space $ G/H $
of a connected Lie group $ G $
such that in the Lie algebra $ \mathfrak g $
of $ G $
there is an $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $-
invariant subspace complementary to the subalgebra $ \mathfrak h \subset \mathfrak g $,
where $ \mathfrak h $
is the Lie algebra of the group $ H $.
The validity of any of the following conditions is sufficient for the homogeneous space $ G/H $
to be reductive: 1) the linear group $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $
is completely reducible; or 2) in $ \mathfrak g $
there is an $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $-
invariant bilinear form whose restriction to $ \mathfrak h $
is non-degenerate. In particular, any homogeneous Riemannian space is reductive. If $ M = G/H $
is a reductive space and the group $ G $
acts effectively on $ M $,
then the linear representation of the isotropy group $ H $
in the tangent space $ M _ {0} $
to the manifold $ M $
at the point $ 0 = eH \in M $
is faithful (cf. Faithful representation). Two important $ G $-
invariant affine connections on $ M $
are associated with each $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $-
invariant subspace $ \mathfrak m \subset \mathfrak g $
complementary to $ \mathfrak h $:
the canonical connection and the natural torsion-free connection. The canonical connection on the reductive space $ M = G/H $
with a fixed $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $-
invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $
is the unique $ G $-
invariant affine connection on $ M $
such that for any vector $ X \in \mathfrak m $
and any frame $ u $
at the point 0, the curve $ ( \mathop{\rm exp} tX) u $
in the principal fibration of frames over $ M $
is horizontal. The canonical connection is complete and the set of its geodesics through 0 coincides with the set of curves of the type $ ( \mathop{\rm exp} tX) 0 $,
where $ X \in \mathfrak m $.
After the natural identification of the spaces $ \mathfrak m $
and $ M _ {0} $,
the curvature tensor $ R $
and torsion tensor $ T $
of the canonical connection are defined by the formulas $ ( R( X, Y) Z) _ {0} = - [[ X, Y] _ {\mathfrak h} , Z] $
and $ T( X, Y) _ {0} = -[ X, Y] _ {\mathfrak m} $,
where $ X, Y, Z \in \mathfrak m $
and $ W _ {\mathfrak h} $
and $ W _ {\mathfrak m} $
denote the projections of the vector $ W \in \mathfrak g $
onto $ \mathfrak h $
and $ \mathfrak m $,
respectively.
The tensor fields $ R $ and $ T $ are parallel relative to the canonical connection, as is any other $ G $- invariant tensor field on $ M $. The Lie algebra of the linear holonomy group (see Holonomy group) of the canonical connections on $ M $ with supporting point 0 is generated by the set $ \{ {\lambda ([ X, Y] _ {\mathfrak h} ) } : {X, Y \in \mathfrak m } \} $, where $ \lambda $ is the linear representation of the isotropy Lie algebra $ \mathfrak h $ in the space $ M _ {0} $. Any connected simply-connected manifold with a complete affine connection with parallel curvature and torsion fields can be represented as a reductive space whose canonical connection coincides with the given affine connection. In the reductive space $ M = G/H $ with fixed $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $ there is a unique $ G $- invariant affine connection with zero torsion having the same geodesics as the canonical connection. This connection is called the natural torsion-free connection on $ M $( relative to the decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $). A homogeneous Riemannian or pseudo-Riemannian space $ M = G/H $ is naturally reductive if it admits an $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $ such that
$$ \tag{* } B( X, [ Z, Y] _ {\mathfrak m} ) + B ([ Z, X] _ {\mathfrak m} , Y) = 0 $$
for all $ X, Y, Z \in \mathfrak m $, where $ B $ is the non-degenerate symmetric bilinear form on $ \mathfrak m $ induced by the Riemannian (pseudo-Riemannian) structure on $ M $ under the natural identification of the spaces $ \mathfrak m $ and $ M _ {0} $. If $ M = G/H $ is a naturally reductive Riemannian or pseudo-Riemannian space with a fixed $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- invariant decomposition $ \mathfrak g = \mathfrak h \dot{+} \mathfrak m $ that satisfies condition (*), then the natural torsion-free connection coincides with the corresponding Riemannian or pseudo-Riemannian connection on $ M $. If $ M $ is a simply-connected naturally reductive homogeneous Riemannian space and $ M = M _ {0} \times \dots \times M _ {r} $ is its de Rham decomposition, then $ M $ can be represented in the form $ M = G/H $; moreover, $ G = G _ {0} \times \dots \times G _ {r} $, $ H = H _ {0} \times \dots \times H _ {r} $ and $ M _ {i} = G _ {i} /H _ {i} $ $ ( i = 0 \dots r) $.
An important generalization of reductive spaces are $ \nu $- reductive homogeneous spaces [4]. A homogeneous space $ G/H $ is called $ \nu $- reductive if its stationary subalgebra $ \mathfrak h $ equals $ \mathfrak h _ {1} \dot{+} \dots \dot{+} \mathfrak h _ \nu $, where $ \mathfrak h _ \nu \neq \{ 0 \} $, and if there is a subspace $ \mathfrak m $ in $ \mathfrak h $ complementary to $ \mathfrak h $ such that $ [ \mathfrak h _ {i} , \mathfrak m ] \subset \mathfrak h _ {i-} 1 $, $ i = 1 \dots \nu $, where $ \mathfrak h _ {0} = \mathfrak m $. The $ 1 $- reductive homogeneous spaces are in fact reductive spaces; examples of $ 2 $- reductive homogeneous spaces are projective (and conformal) spaces on which a group of projective (or conformal) transformations acts. If $ M = G/H $ there is a $ \nu $- reductive homogeneous space and if $ \nu > 1 $, then the linear representation of the isotropy Lie algebra $ \mathfrak h $ is not faithful (since $ [ \mathfrak h _ {i} , \mathfrak m ] \subset \mathfrak h $ when $ i > 1 $); consequently, there is no $ G $- invariant affine connection on $ M $. However, there is a canonical $ G $- invariant connection on a $ \nu $- reductive homogeneous space with the homogeneous space of some transitive-differential group of order $ \nu $ as fibre (see [4]). Reductive and $ \nu $- reductive spaces are characterized as maximally homogeneous $ G $- structures (cf. $ G $- structure) of appropriate type (cf. [6]).
In addition to reductive spaces, partially reductive spaces are also examined, i.e. homogeneous spaces $ G/H $ such that there is a decomposition of the Lie algebra $ \mathfrak g $ into a direct sum of two non-zero $ \mathop{\rm Ad} _ {\mathfrak g} ( H) $- invariant subspaces, one of which contains the subalgebra $ \mathfrak h $( see [5]).
References
| [1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969) |
| [2] | P.K. Rashevskii, "On the geometry of homogeneous spaces" Trudy Sem. Vektor. i Tenzor. Anal. , 9 (1952) pp. 49–74 |
| [3] | K. Nomizu, "Invariant affine connections on homogeneous spaces" Amer. J. Math. , 76 : 1 (1954) pp. 33–65 |
| [4] | I.L. Kantor, "Transitive differential groups and invariant connections in homogeneous spaces" Trudy Sem. Vektor. i Tenzor. Anal. , 13 (1966) pp. 310–398 |
| [5] | E.B. Vinberg, "Invariant linear connections in a homogeneous space" Trudy Moskov. Mat. Obshch. , 9 (1960) pp. 191–210 (In Russian) |
| [6] | D.V. Alekseevskii, "Maximally homogeneous 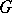 -structures and filtered Lie algebras" Soviet Math. Dokl. , 37 : 2 (1988) pp. 381–384 Dokl. Akad. Nauk SSSR , 299 : 3 (1988) pp. 521–526 -structures and filtered Lie algebras" Soviet Math. Dokl. , 37 : 2 (1988) pp. 381–384 Dokl. Akad. Nauk SSSR , 299 : 3 (1988) pp. 521–526 |
Comments
References
| [a1] | J.A. Wolf, "Spaces of constant curvature" , McGraw-Hill (1967) |
Reductive space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reductive_space&oldid=11232