Difference between revisions of "Abstract analytic number theory"
(Importing text file) |
(latex details) |
||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 154 formulas, 152 were replaced by TEX code.--> | |
| − | |||
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | The central concept in abstract analytic number theory is that of an arithmetical semi-group $G$ (defined below). It turns out that the study of such semi-groups and of (real- or complex-valued) functions on them makes it possible on the one hand to apply methods of classical [[Analytic number theory|analytic number theory]] in a unified way to a variety of asymptotic enumeration questions for isomorphism classes of different kinds of explicit mathematical objects. On the other hand, these procedures also lead to abstract generalizations and analogues of ordinary analytic number theory, which may then be applied in a unified way to further enumeration questions about the (mostly non-arithmetical) concrete types of mathematical objects just alluded to. | ||
| − | |||
| − | + | ==Arithmetical semi-groups== | |
| + | An arithmetical semi-group is, by definition, a commutative [[Semi-group|semi-group]] $G$ with identity element $1$, which contains a countable subset $P$ such that every element $a \ne 1$ in $G$ admits a unique factorization into a finite product of powers of elements of $P$, together with a real-valued mapping $\vert \cdot \vert$ on $G$ such that: | ||
| − | + | i) $|1| = 1$, $|p| > 1$ for $p \in P$; | |
| − | + | ii) $|a b| = |a| \cdot |b|$ for all $a\,,b \in G$; | |
| − | + | iii) the total number of elements $a$ with $|a| < x$ is finite, for each $x > 0$. | |
| − | + | The elements of $P$ are called the primes of $G$, and $\vert \cdot \vert$ is called the norm mapping on $G$. It is obvious that, corresponding to any fixed $c>1$, the definition $\partial(a) = \log_c|a|$ yields a mapping $\partial$ on $G$ such that: | |
| − | + | A) $\partial(1)=0$, $\partial(p)>0$ for $p \in P$; | |
| − | + | B) $\partial(ab) = \partial(a) + \partial(b)$ for all $a\,,b \in G$; | |
| − | + | C) the total number of elements $a$ with $\partial(a) \le x$ is finite, for each $x > 0$. | |
| − | ( | + | Conversely, any real-valued mapping $\partial$ with the properties A)–C) yields a norm on $G$, if one defines $|a| = c^{\partial(a)}$. In cases where such a mapping $\partial$ is of primary interest, $G$ together with $\partial$ is called an additive arithmetical semi-group, and one refers to $\partial$ as the degree mapping on $G$. In most concrete examples of interest, it turns out that the norm or degree mappings represent natural "size" or "dimension" measures which are integer-valued. With an eye to applications to natural examples there is therefore little loss in henceforth restricting attention to either a single integer-valued norm mapping $\vert\cdot\vert$, or a single integer-valued degree mapping $\partial$, on $G$. Depending on which case is being considered, special interest then attaches to the basic counting functions (for $n \in \mathbb{Z}$) |
| + | $$ | ||
| + | G(n) = \#\{ a \in G : |a| = n \} | ||
| + | $$ | ||
| + | $$ | ||
| + | P(n) = \#\{ p \in P : |p| = n \} | ||
| + | $$ | ||
| − | + | (or $G^\sharp(n) = \#\{ a \in G : \partial(a) = n \}$, $P^\sharp(n) = \#\{ p \in P : \partial(p) = n \}$, in the additive case). | |
| − | The | + | The prototype of all arithmetical semi-groups is of course the multiplicative semi-group $\mathbb{N}$ of all positive integers $\{1,2,3,\ldots\}$, with its subset $P_{\mathbb{N}}$ of all rational prime numbers $\{2,3,5,7,\ldots\}$. Here one may define the norm of an integer $|n|$ to be $n$, so that the number $\mathbb{N}(n) = 1$ for $n \ge 1$. |
| − | + | The asymptotic behaviour of $\pi(X) = \sum_{n \le x} P_{\mathbb{N}}(n)$ for large $x$ forms the content of the famous [[prime number theorem]], which states that | |
| + | $$ | ||
| + | \pi(x) \sim \frac{x}{\log x} \ \text{as}\ x \rightarrow \infty | ||
| + | $$ | ||
| + | (cf. also [[De la Vallée-Poussin theorem|de la Vallée-Poussin theorem]]). A suitably generalized form of this theorem holds for many other naturally-occurring arithmetical semi-groups. For example, it is true for the multiplicative semi-group $G_K$ of all non-zero ideals in the [[Ring|ring]] $R = R(K)$ of all algebraic integers in a given [[Algebraic number|algebraic number]] field $K$, with $|I| = \mathop{card}(R/I)$ for any non-zero ideal $I$ in $R$. Here, the prime ideals act as prime elements of the semi-group $G_K$. | ||
| − | + | A simple but nevertheless interesting example of an additive arithmetical semi-group is provided by the multiplicative semi-group $G-q$ of all monic polynomials in one indeterminate $X$ over a [[Finite field|finite field]] $\mathbb{F}_q$ with $q$ elements, with $\partial a = \mathrm{deg}\, a$ and the set $P_q$ of prime elements represented by the irreducible polynomials (cf. also [[Irreducible polynomial|Irreducible polynomial]]). Here, $G_q^\sharp(n) = q^n$, and it can be proved that | |
| + | $$ | ||
| + | P_q^\sharp (n) = \frac{1}{n} \sum_{r | n} \mu(r) q^{n/r} | ||
| + | $$ | ||
| + | where $\mu$ is the classical [[Möbius function]] on $\mathbb{N}$. | ||
| − | + | Up to isomorphism, $G_q$ is the simplest special case of the semi-group $G_R$ of all non-zero ideals in the ring $R = R(K)$ of all integral functions in an algebraic function field $K$ in one variable $K$ over $\mathbb{F}_q$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Up to isomorphism, | ||
===Arithmetical categories of semi-groups.=== | ===Arithmetical categories of semi-groups.=== | ||
Many interesting examples of concrete, but non-classical, arithmetical semi-groups can be found by considering certain specific classes of mathematical objects, such as groups, rings, topological spaces, and so on, together with appropriate "direct product" operations and isomorphism relations for those classes. It is convenient, though admittedly not quite precise, to temporarily ignore the corresponding morphisms and refer to such classes of objects as "categories" (cf. also [[Category|Category]]). | Many interesting examples of concrete, but non-classical, arithmetical semi-groups can be found by considering certain specific classes of mathematical objects, such as groups, rings, topological spaces, and so on, together with appropriate "direct product" operations and isomorphism relations for those classes. It is convenient, though admittedly not quite precise, to temporarily ignore the corresponding morphisms and refer to such classes of objects as "categories" (cf. also [[Category|Category]]). | ||
| − | Now consider some category | + | Now consider some category $\mathcal{C}$ which admits a direct "product" (or "sum" ) operation $\times$ on its objects. Suppose that this operation $\times$ preserves $\mathcal{C}$-isomorphisms, is commutative and associative up to $\mathcal{C}$-isomorphism, and that $\mathcal{C}$ contains a "zero" object $0$ (unique up to $\mathcal{C}$-isomorphism) such that $A \times 0 \cong A$ for all objects $A$ in $\mathcal{C}$. Then suppose that a theorem of Krull–Schmidt type is valid for $\mathcal{C}$, i.e., suppose that every object $A$ can be expressed as a finite $\times$-product $A \cong P_1 \times \cdots \times P_k$ of objects $P_i$ that are indecomposable with respect to $\times$, in a way that is unique up to permutation of terms and $\mathcal{C}$-isomorphism. In most natural situations at least, one may reformulate these conditions on $\mathcal{C}$ by stating that the various isomorphism classes $\bar A$ of objects $A$ in $\mathcal{C}$ form a set $G_{\mathcal{C}}$ that is |
| − | i) a commutative semi-group with identity with respect to the multiplication operation | + | i) a commutative semi-group with identity with respect to the multiplication operation $\bar A \times \bar B = \overline{A \times B}$; |
| − | ii) a semi-group with the unique factorization property with respect to the isomorphism classes of the indecomposable objects in | + | ii) a semi-group with the unique factorization property with respect to the isomorphism classes of the indecomposable objects in $\mathcal{C}$. |
| − | For this reason, one may call the | + | For this reason, one may call the $\mathcal{C}$-isomorphism classes $\bar P_i$ of indecomposable objects $P$ the "primes" of $\mathcal{C}$ or $G_{\mathcal{C}}$. |
| − | In many interesting cases (some of which are illustrated below), the category | + | In many interesting cases (some of which are illustrated below), the category $\mathcal{C}$ also admits a "norm" function $\vert \cdot \vert$ on objects which is invariant under $\mathcal{C}$-isomorphism and has the following properties: |
| − | i) | + | i) $|0| = 1$, $|P| > 1$ for every indecomposable object $P$; |
| − | ii) | + | ii) $|A \times B| = |A|.|B|$ for all objects $A$, $B$; |
| − | iii) the total number of | + | iii) the total number of $\mathcal{C}$-isomorphism classes of objects $A$ of norm $|A| \le x$ is finite, for each real $x > 0$. |
| − | Obviously, in such circumstances, the definition | + | Obviously, in such circumstances, the definition $|\bar A| = |A|$ provides a norm function on $G_{\mathcal{C}}$ satisfying the required conditions for an arithmetical semi-group. For these reasons, a category $\mathcal{C}$ with such further properties may be called an arithmetical category. |
Now consider some concrete illustrations for the above concepts, taken from [[#References|[a2]]], [[#References|[a3]]]. | Now consider some concrete illustrations for the above concepts, taken from [[#References|[a2]]], [[#References|[a3]]]. | ||
| − | a) (Finite Abelian groups; cf. [[ | + | a) (Finite Abelian groups; cf. [[Abelian group]].) One of the simplest non-trivial examples of an arithmetical category is provided by the category $\mathcal{A}$ of all finite Abelian groups, together with the usual direct product operation and the norm function $|A| = \mathrm{card}(A)$. Here, the Krull–Schmidt theorem reduces to the well-known fundamental theorem on finite Abelian groups, the indecomposable objects of this kind being simply the various [[cyclic group]]s $C_{p^n}$ of prime-power order $p^n$. |
| − | b) The category of all semi-simple associative rings of finite cardinality (cf. also [[ | + | b) The category of all semi-simple associative rings of finite cardinality (cf. also [[Associative rings and algebras]]). |
| − | c) The category of all semi-simple finite-dimensional associate algebras over a given field | + | c) The category of all semi-simple finite-dimensional associate algebras over a given field $F$ (cf. also [[Associative rings and algebras]]; [[Semi-simple ring]]). |
| − | d) The category of all semi-simple finite-dimensional | + | d) The category of all semi-simple finite-dimensional [[Lie algebra]]s over a given field $F$. |
| − | e) The category of all compact simply-connected globally symmetric Riemannian manifolds (cf. also [[ | + | e) The category of all compact simply-connected globally symmetric Riemannian manifolds (cf. also [[Globally symmetric Riemannian space]]). |
| − | f) The category | + | f) The category $\mathcal{T}$ of [[topological space]]s of finite cardinality with the property that a space $Y$ lies in $\mathcal{T}$ if and only if each connected component of $Y$ lies in $\mathcal{T}$. |
==Zeta-functions and enumeration problems.== | ==Zeta-functions and enumeration problems.== | ||
| − | For a given arithmetical semi-group | + | For a given arithmetical semi-group $G$, information on the basic counting functions $G ( n )$, $P ( n )$ can often be obtained, algebraically or with the aid of analysis, via a certain series-production relation called the Euler product formula for $G$. |
| − | Indeed, ignoring questions of convergence for the moment, note that (by the unique factorization into prime elements of | + | Indeed, ignoring questions of convergence for the moment, note that (by the unique factorization into prime elements of $G$) the series |
| − | + | \begin{equation*} \zeta _ { G } ( z ) = \sum _ { n = 1 } ^ { \infty } G ( n ) n ^ { - z } = \sum _ { a \in G } | a | ^ { - z } = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a130/a130050/a130050147.png"/></td> </tr></table> |
| − | + | \begin{equation*} = 1 + \sum | p _ { 1 } | ^ { - r _ { 1 } z } \ldots | p _ {m } | ^ { - r _ { m } z } = \end{equation*} | |
| − | + | \begin{equation*} = \prod _ { p \in P } ( 1 + | p | ^ { - z } + | p | ^ { - 2 z } + \ldots ) = \end{equation*} | |
| − | + | \begin{equation*} = \prod _ { p \in P } ( 1 - | p | ^ { - z } ) ^ { - 1 } = \end{equation*} | |
| − | + | \begin{equation*} = \prod _ { m = 2 } ^ { \infty } ( 1 - m ^ { - z } ) ^ { - P ( m ) }. \end{equation*} | |
| − | As a function of | + | As a function of $z$, $\zeta _ { G } ( z )$ is called the zeta-function of $G$. If $G$ is an additive arithmetical semi-group with $| a | = c ^ { \partial ( a ) }$ for some integer $c > 1$, one may substitute the symbol $y$ for $c ^ { - z }$ and obtain the modified Euler product formula: |
| − | + | \begin{equation*} \sum _ { n = 0 } ^ { \infty } G ^ { \# } ( n ) y ^ { n } = \prod _ { m = 1 } ^ { \infty } ( 1 - y ^ { m } ) ^ { - P ^ { \# } ( m ) }; \end{equation*} | |
| − | then | + | then $Z _ { G } ( y ) = \sum _ { n = 0 } ^ { \infty } G ^ { \# } ( n ) y ^ { n }$ is called the modified zeta-function (or generating function) of $G$. |
Some explicit illustrations of zeta-functions and Euler products are given below. | Some explicit illustrations of zeta-functions and Euler products are given below. | ||
===The Riemann zeta-function.=== | ===The Riemann zeta-function.=== | ||
| − | For the basic semi-group | + | For the basic semi-group $\mathbf{N}$ of positive integers, the [[zeta-function]] is |
| − | + | $$ | |
| − | + | \zeta(z) = \sum_{n=1}^\infty n^{-z} \ ; | |
| − | + | $$ | |
| − | it is called the Riemann zeta-function, and the classical Euler product formula reads: | + | it is called the Riemann zeta-function, and the classical [[Euler product]] formula reads: |
| − | + | $$ | |
| − | + | \zeta(z) = \prod_{\text{primes}\,p\,\text{of}\,\mathbf{N}} \left({ 1 - p^{-z} }\right)^{-1} \ . | |
| + | $$ | ||
===The Dedekind zeta-function.=== | ===The Dedekind zeta-function.=== | ||
| − | Let | + | Let $G _ { K }$ denote the (above-mentioned) arithmetical semi-group of all non-zero "integral" ideals in a given algebraic number field $K$. The zeta-function for $G _ { K }$ is then |
| − | + | \begin{equation*} \zeta _ { K } ( z ) = \sum _ { I \in G _ { K } } | I | ^ { - z } = \sum _ { n = 1 } ^ { \infty } K ( n ) n ^ { - z }, \end{equation*} | |
| − | where | + | where $K ( n )$ denotes the total number of ideals of norm $n$ in $G _ { K }$; it is known as the Dedekind zeta-function of $K$. (See also [[Zeta-function|Zeta-function]].) |
===Monic polynomials over a finite field.=== | ===Monic polynomials over a finite field.=== | ||
| − | For the additive arithmetical semi-group | + | For the additive arithmetical semi-group $G_q$ of all monic polynomials in one indeterminate $X$ over $\mathbf{F} _ { q }$ (see above), the generating function may be written as |
| − | + | \begin{equation*} Z _ { q } ( y ) = \sum _ { n = 0 } ^ { \infty } q ^ { n } y ^ { n } = ( 1 - q y ) ^ { - 1 }, \end{equation*} | |
| − | and the above-mentioned explicit formula for | + | and the above-mentioned explicit formula for $P _ { q } ^ { \# } ( n )$ can be deduced as an algebraic consequence of the Euler product for $G_q$. |
===Finite Abelian groups.=== | ===Finite Abelian groups.=== | ||
| − | For the category | + | For the category $\mathcal{A}$ of all finite Abelian groups, the zeta-function may be written as |
| − | + | \begin{equation*} \zeta _ { A } ( z ) = \sum _ { n = 1 } ^ { \infty } a ( n ) n ^ { - z }, \end{equation*} | |
| − | where | + | where $a ( n )$ denotes the total number of isomorphism classes of Abelian groups of order $n$. The discussion of "primes" in $\mathcal{A}$ given above shows that here the Euler product may be written as a double product |
| − | + | \begin{equation*} \zeta _ { A } ( z ) = \prod _ {\substack{ r \geq 1 \\ \text{primes } p \in \mathbf{N}}} \quad ( 1 - p ^ { - r z } ) ^ { - 1 } = \prod _ { r = 1 } ^ { \infty } \zeta ( r z ), \end{equation*} | |
by the Euler product formula for the Riemann zeta-function. | by the Euler product formula for the Riemann zeta-function. | ||
| − | For the subcategory | + | For the subcategory $\mathcal{A} ( p )$ of all finite Abelian $p$-groups, where $p$ is a fixed prime number (cf. also [[P-group|$p$-group]]), it is natural to regard $\mathcal{A} ( p )$ as an additive arithmetical category, with degree mapping defined by |
| − | + | \begin{equation*} \partial ( A ) = \operatorname { log } _ { p } \operatorname { card } ( A ). \end{equation*} | |
| − | In that case, | + | In that case, $\mathcal{A} ( p )$ has exactly one prime of degree $r$ for each $r = 1,2 , \dots$. Therefore the Euler product formula implies that $\mathcal{A} ( p )$ has the generating function |
| − | + | \begin{equation*} Z _ { \mathcal{A} ( p ) } ( y ) = \prod _ { r = 1 } ^ { \infty } ( 1 - y ^ { r } ) ^ { - 1 } = \sum _ { n = 0 } ^ { \infty } \mathbf{p} ( n ) y ^ { n }, \end{equation*} | |
| − | where | + | where $\mathbf{ p} ( n ) = a ( p ^ { n } )$ is the total number of isomorphism classes of Abelian groups of degree $n$ in the above sense. In fact, for $n > 0$, $\mathbf{p} ( n )$ equals the total number of ways of partitioning $n$ into a sum of positive integers, which is also the number of pseudo-metrizable finite topological spaces of cardinality $n$ (see f) above). Thus, the corresponding latter category $\mathcal{P}$ (say) has the same generating function as $\mathcal{A} ( p )$. |
==Types of arithmetical semi-groups.== | ==Types of arithmetical semi-groups.== | ||
Bearing in mind the emphasis on concrete realizations of arithmetical semi-groups in a variety of areas of mathematics, it is reasonable to classify them and to base further investigations according to common features which may be exhibited by the initial enumeration theorems for particular sets of examples. In that way, further questions and enumeration problems may be investigated uniformly under suitable covering assumptions or "axioms" appropriate for particular natural sets of examples. On this basis, a small number of special types of arithmetical semi-groups have so far (2000) been found to predominate amongst natural concrete examples. | Bearing in mind the emphasis on concrete realizations of arithmetical semi-groups in a variety of areas of mathematics, it is reasonable to classify them and to base further investigations according to common features which may be exhibited by the initial enumeration theorems for particular sets of examples. In that way, further questions and enumeration problems may be investigated uniformly under suitable covering assumptions or "axioms" appropriate for particular natural sets of examples. On this basis, a small number of special types of arithmetical semi-groups have so far (2000) been found to predominate amongst natural concrete examples. | ||
| − | ===Classical and axiom- | + | ===Classical and axiom-$A$ type semi-groups.=== |
The strictly classical arithmetical semi-groups of analytic number theory are the multiplicative semi-group of all positive integers and the multiplicative semi-group of all non-zero ideals in the ring of all algebraic integers in a given algebraic number field (see above). For example, H. Weber and E. Landau proved theorems to the effect that | The strictly classical arithmetical semi-groups of analytic number theory are the multiplicative semi-group of all positive integers and the multiplicative semi-group of all non-zero ideals in the ring of all algebraic integers in a given algebraic number field (see above). For example, H. Weber and E. Landau proved theorems to the effect that | ||
| − | + | \begin{equation} \tag{a1} \sum _ { n \leq x } G _ { K } ( n ) = A _ { K } x + O ( x ^ { \eta_K} ) \text { as } x \rightarrow \infty, \end{equation} | |
| − | where | + | where $G _ { K }$ is the semi-group of all "integral" ideals in a given algebraic number field $K$. Landau in particular used (a1) in order to extend many asymptotic results about arithmetical functions on $\mathbf{N}$ to similar functions on $G _ { K }$. |
| − | In quite a different direction, P. Erdős and G. Szekeres proved in 1934 for the category | + | In quite a different direction, P. Erdős and G. Szekeres proved in 1934 for the category $\mathcal{A}$ of all finite Abelian groups that |
| − | + | \begin{equation} \tag{a2} \sum _ { n \leq x } a ( n ) = A _ { 1 } x + O ( \sqrt { x } ) \quad \text { as } x \rightarrow \infty, \end{equation} | |
| − | where | + | where $A _ { 1 } = \prod _ { r \leq 2 } \zeta ( r ) = 2.29\dots$. |
| − | At a later stage, for the category | + | At a later stage, for the category $\mathcal{S}$ of semi-simple finite rings, I.G. Connell and J. Knopfmacher independently proved that |
| − | + | \begin{equation} \tag{a3} \sum _ { n \leq x } S ( n ) = A _ { 2 } x + O ( \sqrt { x } ) \quad \text { as } x \rightarrow \infty, \end{equation} | |
| − | where | + | where $A _ { 2 } = \prod _ { rm ^ { 2 } \geq 2 } ^ { 2 } \zeta ( rm ^ { 2 } ) = 2.49 \dots$. |
| − | Strong concrete motivation was available for unifying certain further developments under the umbrella of general studies of an abstract arithmetical semi-group | + | Strong concrete motivation was available for unifying certain further developments under the umbrella of general studies of an abstract arithmetical semi-group $G$ satisfying the so-called axiom $A$: There exist constants $A _ { G } > 0$, $\delta > 0$ and $\eta < \delta$ (all depending on $G$), such that |
| − | + | \begin{equation*} \sum _ { n \leq x } G ( n ) = A _ { G } x ^ { \delta } + O ( x ^ { \eta } ) \text { as } x \rightarrow \infty . \end{equation*} | |
| − | Theorems based on the assumption of axiom | + | Theorems based on the assumption of axiom $A$ often simultaneously generalize earlier results for $\mathbf{N}$, $G _ { K }$ and $G_{\mathcal{A}}$, and provide additional asymptotic enumeration theorems for a variety of arithmetical categories like $\mathcal{S}$ and many others. |
| − | ===Axiom | + | ===Axiom $A ^ { \# }$ type semi-groups.=== |
| − | Consideration of the examples of multiplicative semi-groups of monic polynomials in one indeterminate, and also of enumeration theorems for some infinite families of explicit additive arithmetical categories connected with rings of integral functions in algebraic function fields over | + | Consideration of the examples of multiplicative semi-groups of monic polynomials in one indeterminate, and also of enumeration theorems for some infinite families of explicit additive arithmetical categories connected with rings of integral functions in algebraic function fields over $\mathbf{F} _ { q }$ (cf. [[#References|[a4]]], [[#References|[a5]]]), provides a wealth of motivation for studying an abstract additive arithmetical semi-group $G$ satisfying axiom $A ^ { \# }$: There exist constants $A _ { G } > 0$, $q > 1$ and $\nu < 1$ (all depending on $G$) such that |
| − | + | \begin{equation*} G ^ { \# } ( n ) = A _ { G } q ^ { n } + O ( q ^ { \nu n } ) \text { as } n \rightarrow \infty. \end{equation*} | |
| − | With this axiom as a basis instead of axiom | + | With this axiom as a basis instead of axiom $A$, problems similar to those outlined above may be investigated, with similar motivation to those stimulating the axiom-$A$ type studies. It then turns out that the ensuing results and methods of proof sometimes but not always possess parallels to those subject to axiom $A$. |
| − | A curious illustration of a non-parallel result arises with the abstract prime number theorem (or abstract prime element theorem) subject to axiom | + | A curious illustration of a non-parallel result arises with the abstract prime number theorem (or abstract prime element theorem) subject to axiom $A ^ { \# }$. In 1976, Knopfmacher derived such a theorem, on the initial foundation of some plausible-looking lemmas parallel to ones under axiom $A$. However, in 1989 and later, other authors independently found and then closed certain gaps in those lemmas. The combined efforts of various authors then led to a final theorem with two cases, depending on whether or not $Z _ { G } ( - q ^ { - 1 } ) = 0$; contributions to this were made by S.D. Cohen, K.-H. Indlekofer, E. Manstavičius, R. Warlimont and W.-B. Zhang (see e.g. [[#References|[a1]]], [[#References|[a4]]]). |
| − | A strange point about this result is that the case | + | A strange point about this result is that the case $Z _ { G } ( - q ^ { - 1 } ) \neq 0$ holds for all the natural examples which initially motivated axiom $A ^ { \# }$. Although ingenious examples in which $Z _ { G } ( - q ^ { - 1 } ) = 0$ have also been constructed, those found up to now might be viewed as somewhat pathological or contrived. Therefore, in terms of the "natural-example-based approach" to this subject outlined in the beginning, it would not be unreasonable to continue the present (2000) direction of investigation under the combined assumption of axiom $A ^ { \# }$ with the additional axiom |
| − | + | \begin{equation*} Z _ { G } ( - q ^ { - 1 } ) \neq 0. \end{equation*} | |
| − | In fact (see e.g. [[#References|[a3]]], [[#References|[a5]]]) many consequences of axiom | + | In fact (see e.g. [[#References|[a3]]], [[#References|[a5]]]) many consequences of axiom $A ^ { \# }$ are unrelated to the value of $Z _ { G } ( - q ^ { - 1 } )$, and so the simplifying additional axiom would only sometimes become relevant (but nevertheless reasonable to then assume at such a stage). |
| − | ===Axiom | + | ===Axiom $C$.=== |
| − | The examples listed earlier included many involving an additive arithmetical category | + | The examples listed earlier included many involving an additive arithmetical category $\mathcal{C}$ for which $G _ { \cal C } ^ { \# } ( n )$ and $P _ { \mathcal{C} } ^ { \# } ( n )$ have quite a different behaviour from that given by axiom $A ^ { \# }$. Here, although the objects in $\mathcal{C}$ may sometimes be rather complicated, the presently (as of 2000) known structure theorems for those objects often lead to a relatively simple estimation for $P _ { \mathcal{C} } ^ { \# } ( n )$ or $\pi _ { \mathcal{C} } ^ { \# } ( x ) = \sum _ { n \leq x } P _ { \mathcal{C} } ^ { \# } ( n )$. Surprisingly perhaps, it turns out that sharp asymptotic information can then be deduced about $G _ { \cal C } ^ { \# } ( n )$ or $N _ { \mathcal{C} } ^ { \# } ( x ) = \sum _ { n \leq x } G _ { \mathcal{C} } ^ { \# } ( n )$ by methods of classical-type arithmetical partition theory, which were initiated by G.H. Hardy and G. Ramanujan in 1917. These methods belong to a quite different branch of classical [[Analytic number theory|analytic number theory]] from those involved in the earlier discussion of axiom $A$. |
| − | On the basis of these new types of examples as motivation, one is led to investigations of an additive arithmetical semi-group | + | On the basis of these new types of examples as motivation, one is led to investigations of an additive arithmetical semi-group $G$ satisfying axiom $C$: There exist constants $C > 0$, $\kappa > 0$ and $\nu$ (all depending on $G$) such that |
| − | + | \begin{equation*} \pi _ { \mathcal{C} } ^ { \# } ( x ) \sim C x ^ { \kappa } ( \operatorname { log } x ) ^ { \nu } \text { as } x \rightarrow \infty. \end{equation*} | |
| − | A simple example of axiom | + | A simple example of axiom $C$ is provided when $\mathcal{C}$ denotes either the category $\mathcal{A} ( p )$ of finite Abelian $p$-groups (cf. also [[P-group|$p$-group]]), or the category $\mathcal{P}$ of pseudo-metrizable finite topological spaces (cf. also [[Pseudo-metric space|Pseudo-metric space]]). |
| − | Similar formulas hold for the categories of compact simply-connected Lie groups, or semi-simple finite-dimensional Lie algebras over an algebraically closed field | + | Similar formulas hold for the categories of compact simply-connected Lie groups, or semi-simple finite-dimensional Lie algebras over an algebraically closed field $F$ of characteristic zero. |
| − | Asymptotic deductions about | + | Asymptotic deductions about $G ^ { \# } ( n )$ or $N _ { G } ^ { \# } ( x ) = \sum _ { n \leq x } G ^ { \# } ( n )$, subject to axiom $C$, could perhaps be referred to as "inverse additive abstract prime number theorems" . Based on methods of generalized arithmetical partition theory, various theorems of this kind can be derived, as well as results about "average values" of arithmetical functions on $G$, and on asymptotic "densities" of certain subsets of $G$, subject to axiom $C$. |
| − | ===Axiom | + | ===Axiom $G_1$.=== |
| − | Yet another natural class of additive arithmetical semi-groups | + | Yet another natural class of additive arithmetical semi-groups $G$ is provided by those satisfying axiom $G_1$: "Almost all" elements of $G$ are prime, in the sense that $G ^ { \# } ( n ) > 0$ for sufficiently large $n$, and $P ^ { \# } ( n ) \sim G ^ { \# } ( n )$ as $n \rightarrow \infty$. |
| − | It is known that various classes | + | It is known that various classes $\Gamma$ of finite graphs define arithmetical semi-groups with this slightly surprising property. It is also known that, when $k > 1$, the multiplicative semi-group $G _ { k , q }$ of all monic polynomials in $k$ indeterminates $X _ { 1 } , \ldots , X _ { k }$ over a finite field $\mathbf{F} _ { q }$ has the property stipulated in axiom $G_1$. |
See [[Abstract prime number theory|Abstract prime number theory]] for a further discussion of arithmetical semi-groups and their corresponding abstract prime number theorems. | See [[Abstract prime number theory|Abstract prime number theory]] for a further discussion of arithmetical semi-groups and their corresponding abstract prime number theorems. | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table> |
| + | <tr><td valign="top">[a1]</td> <td valign="top"> K.-H. Indlekofer, E. Manstavičius, R. Warlimont, "On a certain class of infinite products with an application to arithmetical semigroups" ''Archiv Math.'' , '''56''' (1991) pp. 446–453</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J. Knopfmacher, "Abstract analytic number theory" , North-Holland (1975) (Reprinted: Dover, 1990)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Knopfmacher, "Analytic arithmetic of algebraic function fields" , M. Dekker (1979)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> W.-B. Zhang, "Elementary proofs of the abstract prime number theorem for algebraic function fields" ''Trans. Amer. Math. Soc.'' , '''332''' (1992) pp. 923–937</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> J. Knopfmacher, W.-B. Zhang, "Number theory arising from finite fields, analytic and probabilistic theory" , M. Dekker (2001)</td></tr> | ||
| + | </table> | ||
Latest revision as of 07:41, 7 February 2024
The central concept in abstract analytic number theory is that of an arithmetical semi-group $G$ (defined below). It turns out that the study of such semi-groups and of (real- or complex-valued) functions on them makes it possible on the one hand to apply methods of classical analytic number theory in a unified way to a variety of asymptotic enumeration questions for isomorphism classes of different kinds of explicit mathematical objects. On the other hand, these procedures also lead to abstract generalizations and analogues of ordinary analytic number theory, which may then be applied in a unified way to further enumeration questions about the (mostly non-arithmetical) concrete types of mathematical objects just alluded to.
Arithmetical semi-groups
An arithmetical semi-group is, by definition, a commutative semi-group $G$ with identity element $1$, which contains a countable subset $P$ such that every element $a \ne 1$ in $G$ admits a unique factorization into a finite product of powers of elements of $P$, together with a real-valued mapping $\vert \cdot \vert$ on $G$ such that:
i) $|1| = 1$, $|p| > 1$ for $p \in P$;
ii) $|a b| = |a| \cdot |b|$ for all $a\,,b \in G$;
iii) the total number of elements $a$ with $|a| < x$ is finite, for each $x > 0$.
The elements of $P$ are called the primes of $G$, and $\vert \cdot \vert$ is called the norm mapping on $G$. It is obvious that, corresponding to any fixed $c>1$, the definition $\partial(a) = \log_c|a|$ yields a mapping $\partial$ on $G$ such that:
A) $\partial(1)=0$, $\partial(p)>0$ for $p \in P$;
B) $\partial(ab) = \partial(a) + \partial(b)$ for all $a\,,b \in G$;
C) the total number of elements $a$ with $\partial(a) \le x$ is finite, for each $x > 0$.
Conversely, any real-valued mapping $\partial$ with the properties A)–C) yields a norm on $G$, if one defines $|a| = c^{\partial(a)}$. In cases where such a mapping $\partial$ is of primary interest, $G$ together with $\partial$ is called an additive arithmetical semi-group, and one refers to $\partial$ as the degree mapping on $G$. In most concrete examples of interest, it turns out that the norm or degree mappings represent natural "size" or "dimension" measures which are integer-valued. With an eye to applications to natural examples there is therefore little loss in henceforth restricting attention to either a single integer-valued norm mapping $\vert\cdot\vert$, or a single integer-valued degree mapping $\partial$, on $G$. Depending on which case is being considered, special interest then attaches to the basic counting functions (for $n \in \mathbb{Z}$) $$ G(n) = \#\{ a \in G : |a| = n \} $$ $$ P(n) = \#\{ p \in P : |p| = n \} $$
(or $G^\sharp(n) = \#\{ a \in G : \partial(a) = n \}$, $P^\sharp(n) = \#\{ p \in P : \partial(p) = n \}$, in the additive case).
The prototype of all arithmetical semi-groups is of course the multiplicative semi-group $\mathbb{N}$ of all positive integers $\{1,2,3,\ldots\}$, with its subset $P_{\mathbb{N}}$ of all rational prime numbers $\{2,3,5,7,\ldots\}$. Here one may define the norm of an integer $|n|$ to be $n$, so that the number $\mathbb{N}(n) = 1$ for $n \ge 1$.
The asymptotic behaviour of $\pi(X) = \sum_{n \le x} P_{\mathbb{N}}(n)$ for large $x$ forms the content of the famous prime number theorem, which states that $$ \pi(x) \sim \frac{x}{\log x} \ \text{as}\ x \rightarrow \infty $$ (cf. also de la Vallée-Poussin theorem). A suitably generalized form of this theorem holds for many other naturally-occurring arithmetical semi-groups. For example, it is true for the multiplicative semi-group $G_K$ of all non-zero ideals in the ring $R = R(K)$ of all algebraic integers in a given algebraic number field $K$, with $|I| = \mathop{card}(R/I)$ for any non-zero ideal $I$ in $R$. Here, the prime ideals act as prime elements of the semi-group $G_K$.
A simple but nevertheless interesting example of an additive arithmetical semi-group is provided by the multiplicative semi-group $G-q$ of all monic polynomials in one indeterminate $X$ over a finite field $\mathbb{F}_q$ with $q$ elements, with $\partial a = \mathrm{deg}\, a$ and the set $P_q$ of prime elements represented by the irreducible polynomials (cf. also Irreducible polynomial). Here, $G_q^\sharp(n) = q^n$, and it can be proved that $$ P_q^\sharp (n) = \frac{1}{n} \sum_{r | n} \mu(r) q^{n/r} $$ where $\mu$ is the classical Möbius function on $\mathbb{N}$.
Up to isomorphism, $G_q$ is the simplest special case of the semi-group $G_R$ of all non-zero ideals in the ring $R = R(K)$ of all integral functions in an algebraic function field $K$ in one variable $K$ over $\mathbb{F}_q$.
Arithmetical categories of semi-groups.
Many interesting examples of concrete, but non-classical, arithmetical semi-groups can be found by considering certain specific classes of mathematical objects, such as groups, rings, topological spaces, and so on, together with appropriate "direct product" operations and isomorphism relations for those classes. It is convenient, though admittedly not quite precise, to temporarily ignore the corresponding morphisms and refer to such classes of objects as "categories" (cf. also Category).
Now consider some category $\mathcal{C}$ which admits a direct "product" (or "sum" ) operation $\times$ on its objects. Suppose that this operation $\times$ preserves $\mathcal{C}$-isomorphisms, is commutative and associative up to $\mathcal{C}$-isomorphism, and that $\mathcal{C}$ contains a "zero" object $0$ (unique up to $\mathcal{C}$-isomorphism) such that $A \times 0 \cong A$ for all objects $A$ in $\mathcal{C}$. Then suppose that a theorem of Krull–Schmidt type is valid for $\mathcal{C}$, i.e., suppose that every object $A$ can be expressed as a finite $\times$-product $A \cong P_1 \times \cdots \times P_k$ of objects $P_i$ that are indecomposable with respect to $\times$, in a way that is unique up to permutation of terms and $\mathcal{C}$-isomorphism. In most natural situations at least, one may reformulate these conditions on $\mathcal{C}$ by stating that the various isomorphism classes $\bar A$ of objects $A$ in $\mathcal{C}$ form a set $G_{\mathcal{C}}$ that is
i) a commutative semi-group with identity with respect to the multiplication operation $\bar A \times \bar B = \overline{A \times B}$;
ii) a semi-group with the unique factorization property with respect to the isomorphism classes of the indecomposable objects in $\mathcal{C}$.
For this reason, one may call the $\mathcal{C}$-isomorphism classes $\bar P_i$ of indecomposable objects $P$ the "primes" of $\mathcal{C}$ or $G_{\mathcal{C}}$.
In many interesting cases (some of which are illustrated below), the category $\mathcal{C}$ also admits a "norm" function $\vert \cdot \vert$ on objects which is invariant under $\mathcal{C}$-isomorphism and has the following properties:
i) $|0| = 1$, $|P| > 1$ for every indecomposable object $P$;
ii) $|A \times B| = |A|.|B|$ for all objects $A$, $B$;
iii) the total number of $\mathcal{C}$-isomorphism classes of objects $A$ of norm $|A| \le x$ is finite, for each real $x > 0$.
Obviously, in such circumstances, the definition $|\bar A| = |A|$ provides a norm function on $G_{\mathcal{C}}$ satisfying the required conditions for an arithmetical semi-group. For these reasons, a category $\mathcal{C}$ with such further properties may be called an arithmetical category.
Now consider some concrete illustrations for the above concepts, taken from [a2], [a3].
a) (Finite Abelian groups; cf. Abelian group.) One of the simplest non-trivial examples of an arithmetical category is provided by the category $\mathcal{A}$ of all finite Abelian groups, together with the usual direct product operation and the norm function $|A| = \mathrm{card}(A)$. Here, the Krull–Schmidt theorem reduces to the well-known fundamental theorem on finite Abelian groups, the indecomposable objects of this kind being simply the various cyclic groups $C_{p^n}$ of prime-power order $p^n$.
b) The category of all semi-simple associative rings of finite cardinality (cf. also Associative rings and algebras).
c) The category of all semi-simple finite-dimensional associate algebras over a given field $F$ (cf. also Associative rings and algebras; Semi-simple ring).
d) The category of all semi-simple finite-dimensional Lie algebras over a given field $F$.
e) The category of all compact simply-connected globally symmetric Riemannian manifolds (cf. also Globally symmetric Riemannian space).
f) The category $\mathcal{T}$ of topological spaces of finite cardinality with the property that a space $Y$ lies in $\mathcal{T}$ if and only if each connected component of $Y$ lies in $\mathcal{T}$.
Zeta-functions and enumeration problems.
For a given arithmetical semi-group $G$, information on the basic counting functions $G ( n )$, $P ( n )$ can often be obtained, algebraically or with the aid of analysis, via a certain series-production relation called the Euler product formula for $G$.
Indeed, ignoring questions of convergence for the moment, note that (by the unique factorization into prime elements of $G$) the series
\begin{equation*} \zeta _ { G } ( z ) = \sum _ { n = 1 } ^ { \infty } G ( n ) n ^ { - z } = \sum _ { a \in G } | a | ^ { - z } = \end{equation*}
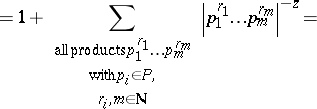 |
\begin{equation*} = 1 + \sum | p _ { 1 } | ^ { - r _ { 1 } z } \ldots | p _ {m } | ^ { - r _ { m } z } = \end{equation*}
\begin{equation*} = \prod _ { p \in P } ( 1 + | p | ^ { - z } + | p | ^ { - 2 z } + \ldots ) = \end{equation*}
\begin{equation*} = \prod _ { p \in P } ( 1 - | p | ^ { - z } ) ^ { - 1 } = \end{equation*}
\begin{equation*} = \prod _ { m = 2 } ^ { \infty } ( 1 - m ^ { - z } ) ^ { - P ( m ) }. \end{equation*}
As a function of $z$, $\zeta _ { G } ( z )$ is called the zeta-function of $G$. If $G$ is an additive arithmetical semi-group with $| a | = c ^ { \partial ( a ) }$ for some integer $c > 1$, one may substitute the symbol $y$ for $c ^ { - z }$ and obtain the modified Euler product formula:
\begin{equation*} \sum _ { n = 0 } ^ { \infty } G ^ { \# } ( n ) y ^ { n } = \prod _ { m = 1 } ^ { \infty } ( 1 - y ^ { m } ) ^ { - P ^ { \# } ( m ) }; \end{equation*}
then $Z _ { G } ( y ) = \sum _ { n = 0 } ^ { \infty } G ^ { \# } ( n ) y ^ { n }$ is called the modified zeta-function (or generating function) of $G$.
Some explicit illustrations of zeta-functions and Euler products are given below.
The Riemann zeta-function.
For the basic semi-group $\mathbf{N}$ of positive integers, the zeta-function is $$ \zeta(z) = \sum_{n=1}^\infty n^{-z} \ ; $$ it is called the Riemann zeta-function, and the classical Euler product formula reads: $$ \zeta(z) = \prod_{\text{primes}\,p\,\text{of}\,\mathbf{N}} \left({ 1 - p^{-z} }\right)^{-1} \ . $$
The Dedekind zeta-function.
Let $G _ { K }$ denote the (above-mentioned) arithmetical semi-group of all non-zero "integral" ideals in a given algebraic number field $K$. The zeta-function for $G _ { K }$ is then
\begin{equation*} \zeta _ { K } ( z ) = \sum _ { I \in G _ { K } } | I | ^ { - z } = \sum _ { n = 1 } ^ { \infty } K ( n ) n ^ { - z }, \end{equation*}
where $K ( n )$ denotes the total number of ideals of norm $n$ in $G _ { K }$; it is known as the Dedekind zeta-function of $K$. (See also Zeta-function.)
Monic polynomials over a finite field.
For the additive arithmetical semi-group $G_q$ of all monic polynomials in one indeterminate $X$ over $\mathbf{F} _ { q }$ (see above), the generating function may be written as
\begin{equation*} Z _ { q } ( y ) = \sum _ { n = 0 } ^ { \infty } q ^ { n } y ^ { n } = ( 1 - q y ) ^ { - 1 }, \end{equation*}
and the above-mentioned explicit formula for $P _ { q } ^ { \# } ( n )$ can be deduced as an algebraic consequence of the Euler product for $G_q$.
Finite Abelian groups.
For the category $\mathcal{A}$ of all finite Abelian groups, the zeta-function may be written as
\begin{equation*} \zeta _ { A } ( z ) = \sum _ { n = 1 } ^ { \infty } a ( n ) n ^ { - z }, \end{equation*}
where $a ( n )$ denotes the total number of isomorphism classes of Abelian groups of order $n$. The discussion of "primes" in $\mathcal{A}$ given above shows that here the Euler product may be written as a double product
\begin{equation*} \zeta _ { A } ( z ) = \prod _ {\substack{ r \geq 1 \\ \text{primes } p \in \mathbf{N}}} \quad ( 1 - p ^ { - r z } ) ^ { - 1 } = \prod _ { r = 1 } ^ { \infty } \zeta ( r z ), \end{equation*}
by the Euler product formula for the Riemann zeta-function.
For the subcategory $\mathcal{A} ( p )$ of all finite Abelian $p$-groups, where $p$ is a fixed prime number (cf. also $p$-group), it is natural to regard $\mathcal{A} ( p )$ as an additive arithmetical category, with degree mapping defined by
\begin{equation*} \partial ( A ) = \operatorname { log } _ { p } \operatorname { card } ( A ). \end{equation*}
In that case, $\mathcal{A} ( p )$ has exactly one prime of degree $r$ for each $r = 1,2 , \dots$. Therefore the Euler product formula implies that $\mathcal{A} ( p )$ has the generating function
\begin{equation*} Z _ { \mathcal{A} ( p ) } ( y ) = \prod _ { r = 1 } ^ { \infty } ( 1 - y ^ { r } ) ^ { - 1 } = \sum _ { n = 0 } ^ { \infty } \mathbf{p} ( n ) y ^ { n }, \end{equation*}
where $\mathbf{ p} ( n ) = a ( p ^ { n } )$ is the total number of isomorphism classes of Abelian groups of degree $n$ in the above sense. In fact, for $n > 0$, $\mathbf{p} ( n )$ equals the total number of ways of partitioning $n$ into a sum of positive integers, which is also the number of pseudo-metrizable finite topological spaces of cardinality $n$ (see f) above). Thus, the corresponding latter category $\mathcal{P}$ (say) has the same generating function as $\mathcal{A} ( p )$.
Types of arithmetical semi-groups.
Bearing in mind the emphasis on concrete realizations of arithmetical semi-groups in a variety of areas of mathematics, it is reasonable to classify them and to base further investigations according to common features which may be exhibited by the initial enumeration theorems for particular sets of examples. In that way, further questions and enumeration problems may be investigated uniformly under suitable covering assumptions or "axioms" appropriate for particular natural sets of examples. On this basis, a small number of special types of arithmetical semi-groups have so far (2000) been found to predominate amongst natural concrete examples.
Classical and axiom-$A$ type semi-groups.
The strictly classical arithmetical semi-groups of analytic number theory are the multiplicative semi-group of all positive integers and the multiplicative semi-group of all non-zero ideals in the ring of all algebraic integers in a given algebraic number field (see above). For example, H. Weber and E. Landau proved theorems to the effect that
\begin{equation} \tag{a1} \sum _ { n \leq x } G _ { K } ( n ) = A _ { K } x + O ( x ^ { \eta_K} ) \text { as } x \rightarrow \infty, \end{equation}
where $G _ { K }$ is the semi-group of all "integral" ideals in a given algebraic number field $K$. Landau in particular used (a1) in order to extend many asymptotic results about arithmetical functions on $\mathbf{N}$ to similar functions on $G _ { K }$.
In quite a different direction, P. Erdős and G. Szekeres proved in 1934 for the category $\mathcal{A}$ of all finite Abelian groups that
\begin{equation} \tag{a2} \sum _ { n \leq x } a ( n ) = A _ { 1 } x + O ( \sqrt { x } ) \quad \text { as } x \rightarrow \infty, \end{equation}
where $A _ { 1 } = \prod _ { r \leq 2 } \zeta ( r ) = 2.29\dots$.
At a later stage, for the category $\mathcal{S}$ of semi-simple finite rings, I.G. Connell and J. Knopfmacher independently proved that
\begin{equation} \tag{a3} \sum _ { n \leq x } S ( n ) = A _ { 2 } x + O ( \sqrt { x } ) \quad \text { as } x \rightarrow \infty, \end{equation}
where $A _ { 2 } = \prod _ { rm ^ { 2 } \geq 2 } ^ { 2 } \zeta ( rm ^ { 2 } ) = 2.49 \dots$.
Strong concrete motivation was available for unifying certain further developments under the umbrella of general studies of an abstract arithmetical semi-group $G$ satisfying the so-called axiom $A$: There exist constants $A _ { G } > 0$, $\delta > 0$ and $\eta < \delta$ (all depending on $G$), such that
\begin{equation*} \sum _ { n \leq x } G ( n ) = A _ { G } x ^ { \delta } + O ( x ^ { \eta } ) \text { as } x \rightarrow \infty . \end{equation*}
Theorems based on the assumption of axiom $A$ often simultaneously generalize earlier results for $\mathbf{N}$, $G _ { K }$ and $G_{\mathcal{A}}$, and provide additional asymptotic enumeration theorems for a variety of arithmetical categories like $\mathcal{S}$ and many others.
Axiom $A ^ { \# }$ type semi-groups.
Consideration of the examples of multiplicative semi-groups of monic polynomials in one indeterminate, and also of enumeration theorems for some infinite families of explicit additive arithmetical categories connected with rings of integral functions in algebraic function fields over $\mathbf{F} _ { q }$ (cf. [a4], [a5]), provides a wealth of motivation for studying an abstract additive arithmetical semi-group $G$ satisfying axiom $A ^ { \# }$: There exist constants $A _ { G } > 0$, $q > 1$ and $\nu < 1$ (all depending on $G$) such that
\begin{equation*} G ^ { \# } ( n ) = A _ { G } q ^ { n } + O ( q ^ { \nu n } ) \text { as } n \rightarrow \infty. \end{equation*}
With this axiom as a basis instead of axiom $A$, problems similar to those outlined above may be investigated, with similar motivation to those stimulating the axiom-$A$ type studies. It then turns out that the ensuing results and methods of proof sometimes but not always possess parallels to those subject to axiom $A$.
A curious illustration of a non-parallel result arises with the abstract prime number theorem (or abstract prime element theorem) subject to axiom $A ^ { \# }$. In 1976, Knopfmacher derived such a theorem, on the initial foundation of some plausible-looking lemmas parallel to ones under axiom $A$. However, in 1989 and later, other authors independently found and then closed certain gaps in those lemmas. The combined efforts of various authors then led to a final theorem with two cases, depending on whether or not $Z _ { G } ( - q ^ { - 1 } ) = 0$; contributions to this were made by S.D. Cohen, K.-H. Indlekofer, E. Manstavičius, R. Warlimont and W.-B. Zhang (see e.g. [a1], [a4]).
A strange point about this result is that the case $Z _ { G } ( - q ^ { - 1 } ) \neq 0$ holds for all the natural examples which initially motivated axiom $A ^ { \# }$. Although ingenious examples in which $Z _ { G } ( - q ^ { - 1 } ) = 0$ have also been constructed, those found up to now might be viewed as somewhat pathological or contrived. Therefore, in terms of the "natural-example-based approach" to this subject outlined in the beginning, it would not be unreasonable to continue the present (2000) direction of investigation under the combined assumption of axiom $A ^ { \# }$ with the additional axiom
\begin{equation*} Z _ { G } ( - q ^ { - 1 } ) \neq 0. \end{equation*}
In fact (see e.g. [a3], [a5]) many consequences of axiom $A ^ { \# }$ are unrelated to the value of $Z _ { G } ( - q ^ { - 1 } )$, and so the simplifying additional axiom would only sometimes become relevant (but nevertheless reasonable to then assume at such a stage).
Axiom $C$.
The examples listed earlier included many involving an additive arithmetical category $\mathcal{C}$ for which $G _ { \cal C } ^ { \# } ( n )$ and $P _ { \mathcal{C} } ^ { \# } ( n )$ have quite a different behaviour from that given by axiom $A ^ { \# }$. Here, although the objects in $\mathcal{C}$ may sometimes be rather complicated, the presently (as of 2000) known structure theorems for those objects often lead to a relatively simple estimation for $P _ { \mathcal{C} } ^ { \# } ( n )$ or $\pi _ { \mathcal{C} } ^ { \# } ( x ) = \sum _ { n \leq x } P _ { \mathcal{C} } ^ { \# } ( n )$. Surprisingly perhaps, it turns out that sharp asymptotic information can then be deduced about $G _ { \cal C } ^ { \# } ( n )$ or $N _ { \mathcal{C} } ^ { \# } ( x ) = \sum _ { n \leq x } G _ { \mathcal{C} } ^ { \# } ( n )$ by methods of classical-type arithmetical partition theory, which were initiated by G.H. Hardy and G. Ramanujan in 1917. These methods belong to a quite different branch of classical analytic number theory from those involved in the earlier discussion of axiom $A$.
On the basis of these new types of examples as motivation, one is led to investigations of an additive arithmetical semi-group $G$ satisfying axiom $C$: There exist constants $C > 0$, $\kappa > 0$ and $\nu$ (all depending on $G$) such that
\begin{equation*} \pi _ { \mathcal{C} } ^ { \# } ( x ) \sim C x ^ { \kappa } ( \operatorname { log } x ) ^ { \nu } \text { as } x \rightarrow \infty. \end{equation*}
A simple example of axiom $C$ is provided when $\mathcal{C}$ denotes either the category $\mathcal{A} ( p )$ of finite Abelian $p$-groups (cf. also $p$-group), or the category $\mathcal{P}$ of pseudo-metrizable finite topological spaces (cf. also Pseudo-metric space).
Similar formulas hold for the categories of compact simply-connected Lie groups, or semi-simple finite-dimensional Lie algebras over an algebraically closed field $F$ of characteristic zero.
Asymptotic deductions about $G ^ { \# } ( n )$ or $N _ { G } ^ { \# } ( x ) = \sum _ { n \leq x } G ^ { \# } ( n )$, subject to axiom $C$, could perhaps be referred to as "inverse additive abstract prime number theorems" . Based on methods of generalized arithmetical partition theory, various theorems of this kind can be derived, as well as results about "average values" of arithmetical functions on $G$, and on asymptotic "densities" of certain subsets of $G$, subject to axiom $C$.
Axiom $G_1$.
Yet another natural class of additive arithmetical semi-groups $G$ is provided by those satisfying axiom $G_1$: "Almost all" elements of $G$ are prime, in the sense that $G ^ { \# } ( n ) > 0$ for sufficiently large $n$, and $P ^ { \# } ( n ) \sim G ^ { \# } ( n )$ as $n \rightarrow \infty$.
It is known that various classes $\Gamma$ of finite graphs define arithmetical semi-groups with this slightly surprising property. It is also known that, when $k > 1$, the multiplicative semi-group $G _ { k , q }$ of all monic polynomials in $k$ indeterminates $X _ { 1 } , \ldots , X _ { k }$ over a finite field $\mathbf{F} _ { q }$ has the property stipulated in axiom $G_1$.
See Abstract prime number theory for a further discussion of arithmetical semi-groups and their corresponding abstract prime number theorems.
References
| [a1] | K.-H. Indlekofer, E. Manstavičius, R. Warlimont, "On a certain class of infinite products with an application to arithmetical semigroups" Archiv Math. , 56 (1991) pp. 446–453 |
| [a2] | J. Knopfmacher, "Abstract analytic number theory" , North-Holland (1975) (Reprinted: Dover, 1990) |
| [a3] | J. Knopfmacher, "Analytic arithmetic of algebraic function fields" , M. Dekker (1979) |
| [a4] | W.-B. Zhang, "Elementary proofs of the abstract prime number theorem for algebraic function fields" Trans. Amer. Math. Soc. , 332 (1992) pp. 923–937 |
| [a5] | J. Knopfmacher, W.-B. Zhang, "Number theory arising from finite fields, analytic and probabilistic theory" , M. Dekker (2001) |
Abstract analytic number theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abstract_analytic_number_theory&oldid=14794