Difference between revisions of "Schwarz symmetric derivative"
(Importing text file) |
(latex details) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s0835801.png | ||
| + | $#A+1 = 11 n = 1 | ||
| + | $#C+1 = 11 : ~/encyclopedia/old_files/data/S083/S.0803580 Schwarz symmetric derivative | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | ''of a function $ f $ | ||
| + | at a point $ x _ {0} $'' | ||
The value | The value | ||
| − | + | $$ | |
| + | D ^ {2} f( x _ {0} ) = \lim\limits _ {h \rightarrow 0 } | ||
| + | \frac{f( x _ {0} + h)- 2f( x _ {0} )+ f( x _ {0} - h) }{h ^ {2} } | ||
| + | . | ||
| + | $$ | ||
| − | It is sometimes called the [[ | + | It is sometimes called the [[Riemann derivative]] or the second symmetric derivative. For the first time introduced by B. Riemann in 1854 (see [[#References|[2]]]); it was studied by H.A. Schwarz [[#References|[1]]]. More generally, the symmetric derivative of order $ n $ |
| + | is also called a Schwarz symmetric derivative: | ||
| − | + | $$ | |
| + | D ^ {n} f( x) = \lim\limits _ {h \rightarrow 0 } | ||
| + | \frac{\Delta _ {h} ^ {n} f( x) }{h ^ {n} } | ||
| + | = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \lim\limits _ {h \rightarrow 0 } | ||
| + | \frac{\sum_{k=0}^ { n } \left | ||
| + | ( \begin{array}{c} | ||
| + | n \\ | ||
| + | k | ||
| + | \end{array} | ||
| + | \right ) (- 1) ^ {k} f ( x + ( n- 2k ) h / 2 ) }{h ^ {n} } | ||
| + | . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H.A. Schwarz, "Beweis eines für die Theorie der trigonometrischen Reihen in Betracht kommenden Hülfssatzes" , ''Gesammelte Math. Abhandlungen'' , Chelsea, reprint (1972) pp. 341–343</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" H. Weber (ed.) , ''B. Riemann's Gesammelte Mathematische Werke'' , Dover, reprint (1953) pp. 227–271 ((Original: Göttinger Akad. Abh. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083580/s0835808.png" /> (1868)))</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.P. Natanson, "Theory of functions of a real variable" , '''1–2''' , F. Ungar (1955–1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Zygmund, "Trigonometric series" , '''1–2''' , Cambridge Univ. Press (1988)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H.A. Schwarz, "Beweis eines für die Theorie der trigonometrischen Reihen in Betracht kommenden Hülfssatzes" , ''Gesammelte Math. Abhandlungen'' , Chelsea, reprint (1972) pp. 341–343</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" H. Weber (ed.) , ''B. Riemann's Gesammelte Mathematische Werke'' , Dover, reprint (1953) pp. 227–271 ((Original: Göttinger Akad. Abh. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083580/s0835808.png" /> (1868)))</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.P. Natanson, "Theory of functions of a real variable" , '''1–2''' , F. Ungar (1955–1961) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A. Zygmund, "Trigonometric series" , '''1–2''' , Cambridge Univ. Press (1988)</TD></TR></table> | ||
| + | ====Comments==== | ||
| + | The name general derivative is also used for this notion. A natural approach is to start with the central difference $ f( x _ {0} + h/2 ) - f( x _ {0} - h/2) $, | ||
| + | and to define the first symmetric derivative as | ||
| + | $$ | ||
| + | Df( x _ {0} ) = \lim\limits _ {h \rightarrow 0 } \ | ||
| − | = | + | \frac{f( x _ {0} + h/2)- f( x _ {0} - h/2) }{h} |
| − | + | = \ | |
| + | \lim\limits _ {h \rightarrow 0 } \ | ||
| − | + | \frac{\Delta _ {h} f ( x _ {0} ) }{h} | |
| + | , | ||
| + | $$ | ||
| − | and then | + | and then $ D ^ {n} = D( D ^ {n-1} ) $, |
| + | $ n \geq 1 $, | ||
| + | $ D ^ {0} f = f $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24</TD></TR></table> | ||
Latest revision as of 20:00, 15 January 2024
of a function $ f $
at a point $ x _ {0} $
The value
$$ D ^ {2} f( x _ {0} ) = \lim\limits _ {h \rightarrow 0 } \frac{f( x _ {0} + h)- 2f( x _ {0} )+ f( x _ {0} - h) }{h ^ {2} } . $$
It is sometimes called the Riemann derivative or the second symmetric derivative. For the first time introduced by B. Riemann in 1854 (see [2]); it was studied by H.A. Schwarz [1]. More generally, the symmetric derivative of order $ n $ is also called a Schwarz symmetric derivative:
$$ D ^ {n} f( x) = \lim\limits _ {h \rightarrow 0 } \frac{\Delta _ {h} ^ {n} f( x) }{h ^ {n} } = $$
$$ = \ \lim\limits _ {h \rightarrow 0 } \frac{\sum_{k=0}^ { n } \left ( \begin{array}{c} n \\ k \end{array} \right ) (- 1) ^ {k} f ( x + ( n- 2k ) h / 2 ) }{h ^ {n} } . $$
References
| [1] | H.A. Schwarz, "Beweis eines für die Theorie der trigonometrischen Reihen in Betracht kommenden Hülfssatzes" , Gesammelte Math. Abhandlungen , Chelsea, reprint (1972) pp. 341–343 |
| [2] | B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" H. Weber (ed.) , B. Riemann's Gesammelte Mathematische Werke , Dover, reprint (1953) pp. 227–271 ((Original: Göttinger Akad. Abh. 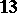 (1868))) (1868))) |
| [3] | I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) |
| [4] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [5] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
Comments
The name general derivative is also used for this notion. A natural approach is to start with the central difference $ f( x _ {0} + h/2 ) - f( x _ {0} - h/2) $, and to define the first symmetric derivative as
$$ Df( x _ {0} ) = \lim\limits _ {h \rightarrow 0 } \ \frac{f( x _ {0} + h/2)- f( x _ {0} - h/2) }{h} = \ \lim\limits _ {h \rightarrow 0 } \ \frac{\Delta _ {h} f ( x _ {0} ) }{h} , $$
and then $ D ^ {n} = D( D ^ {n-1} ) $, $ n \geq 1 $, $ D ^ {0} f = f $.
References
| [a1] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 |
Schwarz symmetric derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schwarz_symmetric_derivative&oldid=15458