Difference between revisions of "Sturm-Liouville problem, inverse"
Ulf Rehmann (talk | contribs) m (moved Sturm–Liouville problem, inverse to Sturm-Liouville problem, inverse: ascii title) |
(latex details) |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s0907801.png | ||
| + | $#A+1 = 145 n = 5 | ||
| + | $#C+1 = 145 : ~/encyclopedia/old_files/data/S090/S.0900780 Sturm\ANDLiouville problem, inverse | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A problem in which it is required to reconstruct a function (a potential) $ q $ | |
| + | from some spectral characteristics of the operator $ A $ | ||
| + | generated by the differential expression $ l[ y] = - y ^ {\prime\prime} + q( x) y $ | ||
| + | and some boundary conditions in the Hilbert space $ L _ {2} ( a, b) $, | ||
| + | where $ x $ | ||
| + | varies in a finite or infinite interval $ ( a, b) $. | ||
| + | Moreover, one should also reconstruct the boundary conditions corresponding to the operator $ A $. | ||
| − | + | When studying inverse problems, the following natural questions arise: 1) to find out which spectral characteristics determine the operator $ A $ | |
| + | uniquely; 2) to give a method of reconstructing the operator $ A $ | ||
| + | from these spectral characteristics; and 3) to find particular properties of the spectral characteristics considered. Depending on the choice of the spectral characteristics, different statements of inverse problems are possible (often arising in applications). | ||
| − | + | The first result concerning inverse problems (see [[#References|[10]]]), which gave a start to the whole theory, is: Let $ \lambda _ {0} , \lambda _ {1} \dots $ | |
| + | be the eigenvalues for the problem | ||
| − | + | $$ \tag{1 } | |
| + | \left . | ||
| − | + | \begin{array}{c} | |
| + | - y ^ {\prime\prime} + q( x) y = \lambda y ,\ 0 \leq x \leq \pi , \\ | ||
| + | y ^ \prime ( 0) = y ^ \prime ( \pi ) = 0, \\ | ||
| + | \end{array} | ||
| − | + | \right \} | |
| + | $$ | ||
| − | + | and let $ q $ | |
| + | be a real-valued continuous function on the interval $ [ 0, \pi ] $. | ||
| + | If $ \lambda _ {n} = n ^ {2} $, | ||
| + | $ n = 0, 1 \dots $ | ||
| + | then $ q( x) \equiv 0 $. | ||
| − | + | A profound study of inverse problems started in the 1940's (see [[#References|[11]]], [[#References|[12]]]). Let $ \lambda _ {0} , \lambda _ {1} \dots $ | |
| + | be the eigenvalues for the equation (1) under the boundary conditions | ||
| − | + | $$ \tag{2 } | |
| + | y ^ \prime ( 0) - hy( 0) = 0,\ \ | ||
| + | y ^ \prime ( \pi ) + Hy( \pi ) = 0 | ||
| + | $$ | ||
| − | + | ( $ h $ | |
| + | and $ H $ | ||
| + | are real numbers), and let $ \mu _ {0} , \mu _ {1} \dots $ | ||
| + | be the eigenvalues of (1) under the boundary conditions | ||
| − | + | $$ | |
| + | y ^ \prime ( 0) - h _ {1} y( 0) = 0,\ \ | ||
| + | y ^ \prime ( \pi ) + Hy( \pi ) = 0 ,\ \ | ||
| + | h _ {1} \neq h. | ||
| + | $$ | ||
| − | + | Then the sequences $ \{ \lambda _ {n} \} $ | |
| + | and $ \{ \mu _ {n} \} $, | ||
| + | $ n = 0, 1 \dots $ | ||
| + | determine the function $ q $ | ||
| + | and the numbers $ h $, | ||
| + | $ h _ {1} $ | ||
| + | and $ H $ | ||
| + | uniquely. Moreover, if at least one eigenvalue in these problems has not been determined, then all the others do not determine the equation (1) uniquely. In particular, generally speaking, one spectrum does not determine the equation uniquely (the above-mentioned result is an exception to the general rule). | ||
| − | + | If the equation (1) is studied on the half-line $ ( 0, \infty ) $ | |
| + | and the potential function $ q $ | ||
| + | satisfies the requirement | ||
| + | |||
| + | $$ | ||
| + | \int\limits _ { 0 } ^ \infty x | q( x) | dx < \infty , | ||
| + | $$ | ||
| + | |||
| + | then the solution $ \phi ( x, \lambda ) $ | ||
| + | of the problem $ - y ^ {\prime\prime} + q( x) y = \lambda ^ {2} y $, | ||
| + | $ y( 0) = 0 $, | ||
| + | has an asymptotic representation for $ x \rightarrow \infty $, | ||
| + | |||
| + | $$ | ||
| + | \phi ( x, \lambda ) = M( \lambda ) \sin [ \lambda x + \delta ( \lambda )] + o( 1). | ||
| + | $$ | ||
| + | |||
| + | The function $ \delta ( \lambda ) $ | ||
| + | is called the scattering phase. The main result is that if a problem (considered in the space $ L _ {2} ( 0, \infty ) $) | ||
| + | does not have discrete eigenvalues, then the scattering phase determines the potential function $ q $ | ||
| + | uniquely. | ||
A decisive step in the further development of the theory of inverse problems was the application of so-called operator-transform techniques (see [[Sturm–Liouville equation|Sturm–Liouville equation]]), which was naturally developed in the framework of the theory of generalized shift operators (see [[#References|[4]]]). | A decisive step in the further development of the theory of inverse problems was the application of so-called operator-transform techniques (see [[Sturm–Liouville equation|Sturm–Liouville equation]]), which was naturally developed in the framework of the theory of generalized shift operators (see [[#References|[4]]]). | ||
| Line 35: | Line 99: | ||
In principle, all inverse problems can be reduced to the inverse problem of reconstructing an operator from its spectral function. However, this way is not always the simplest; moreover, when following it, one often encounters difficulties in finding necessary and sufficient conditions for the spectral characteristics that are used to reconstruct the operator. | In principle, all inverse problems can be reduced to the inverse problem of reconstructing an operator from its spectral function. However, this way is not always the simplest; moreover, when following it, one often encounters difficulties in finding necessary and sufficient conditions for the spectral characteristics that are used to reconstruct the operator. | ||
| − | The significance of inverse problems became greater after discovering a possibility to apply them to solve some non-linear evolution equations of mathematical physics. In particular, a relationship (see [[#References|[25]]]) between inverse problems for some Sturm–Liouville operators with a finite number of gaps in the spectrum and the [[Jacobi inversion problem|Jacobi inversion problem]] for Abelian integrals was established. Recent development of these ideas made it possible to obtain explicit formulas, which express finite gap potentials by Riemann | + | The significance of inverse problems became greater after discovering a possibility to apply them to solve some non-linear evolution equations of mathematical physics. In particular, a relationship (see [[#References|[25]]]) between inverse problems for some Sturm–Liouville operators with a finite number of gaps in the spectrum and the [[Jacobi inversion problem|Jacobi inversion problem]] for Abelian integrals was established. Recent development of these ideas made it possible to obtain explicit formulas, which express finite gap potentials by Riemann $ \theta $- |
| + | functions (see [[#References|[1]]], [[#References|[5]]]). | ||
Below two versions of the statement and solution of inverse problems will be considered. | Below two versions of the statement and solution of inverse problems will be considered. | ||
| − | + | $ 1 $. | |
| + | Given a known spectral function $ \rho ( \lambda ) $, | ||
| + | find a differential equation in the form | ||
| − | + | $$ | |
| + | l[ y] = - y ^ {\prime\prime} + q( x) y | ||
| + | $$ | ||
| − | with a real locally-summable potential | + | with a real locally-summable potential $ q( x) $, |
| + | $ 0 \leq x < \infty $, | ||
| + | and a number $ h $ | ||
| + | appearing in the boundary condition | ||
| − | + | $$ \tag{3 } | |
| + | y ^ \prime ( 0) - hy( 0) = 0. | ||
| + | $$ | ||
To solve this problem it is assumed that | To solve this problem it is assumed that | ||
| − | + | $$ \tag{4 } | |
| + | \Phi ( x) = \int\limits _ {- \infty } ^ { + \infty } | ||
| + | \frac{1 - \cos \sqrt \lambda x } \lambda | ||
| + | |||
| + | d \rho ( \lambda ),\ \ | ||
| + | 0 < x < \infty , | ||
| + | $$ | ||
| − | + | $$ | |
| + | f( x, y) = | ||
| + | \frac{1}{2} | ||
| + | \{ \Phi ^ {\prime\prime} ( x+ y) + \Phi ^ {\prime\prime} ( | x- y | ) \} . | ||
| + | $$ | ||
It turns out that the integral equation | It turns out that the integral equation | ||
| − | + | $$ \tag{5 } | |
| + | f( x, y) + K( x, y) + \int\limits _ { 0 } ^ { x } K( x, t) f( t, y) dt = 0,\ \ | ||
| + | 0 \leq y \leq x, | ||
| + | $$ | ||
| + | |||
| + | has a unique solution $ K( x, y) $ | ||
| + | for each fixed $ x $. | ||
| + | The potential $ q $ | ||
| + | is defined by the formula | ||
| − | + | $$ | |
| + | q( x) = 2 | ||
| + | \frac{dK( x, x) }{dx} | ||
| + | , | ||
| + | $$ | ||
| − | + | and the number $ h $ | |
| + | in (3) is given by the formula $ h = K( 0, 0) $( | ||
| + | see [[#References|[14]]]). The solution $ \phi ( x, y) $ | ||
| + | of the equation $ l [ y] = \lambda y $ | ||
| + | and satisfying the boundary conditions $ \phi ( 0, \lambda ) = 1 $ | ||
| + | and $ \phi ^ \prime ( 0, \lambda ) = h $ | ||
| + | can be found by the formula | ||
| − | + | $$ | |
| + | \phi ( x, \lambda ) = \cos \sqrt \lambda x + \int\limits _ { 0 } ^ { x } K( x, t) \ | ||
| + | \cos \sqrt \lambda t dt. | ||
| + | $$ | ||
| − | < | + | Further, a non-decreasing function $ \rho ( \lambda ) $, |
| + | $ - \infty < \lambda < \infty $, | ||
| + | is the spectral function for some problem $ - y ^ {\prime\prime} + q( x) y = \lambda y $, | ||
| + | $ 0 \leq x < \infty $, | ||
| + | $ y ^ \prime ( 0) - hy( 0) = 0 $, | ||
| + | where $ q $ | ||
| + | is a real-valued function with $ m $ | ||
| + | locally-summable derivatives and $ h $ | ||
| + | is a real number, if and only if the function $ \Phi ( x) $ | ||
| + | constructed from $ \rho ( \lambda ) $ | ||
| + | by formula (4) has $ m+ 3 $ | ||
| + | locally-summable derivatives and $ \Phi ^ {\prime\prime} (+ 0) = - h $( | ||
| + | see [[#References|[14]]], [[#References|[17]]], [[#References|[9]]]). In a number of particular cases, $ q $ | ||
| + | and $ h $ | ||
| + | can be found effectively from the function $ \rho ( \lambda ) $. | ||
| + | For example, let | ||
| − | + | $$ | |
| + | \rho ( \lambda ) = \left \{ | ||
| − | + | \begin{array}{lll} | |
| − | + | \frac{2} \pi | |
| + | \sqrt \lambda + \alpha \chi ( \lambda - \lambda _ {0} ) & \textrm{ for } &\lambda > 0, \\ | ||
| + | \alpha \chi ( \lambda - \lambda _ {0} ) & \textrm{ for } &\lambda < 0, \\ | ||
| + | \end{array} | ||
| − | + | \right .$$ | |
| − | + | where $ \chi ( \lambda ) = 0 $ | |
| + | for $ \lambda < 0 $ | ||
| + | and $ \chi ( \lambda ) = 1 $ | ||
| + | for $ \lambda > 0 $ | ||
| + | and $ \alpha $ | ||
| + | is a positive number. In this case the integral equation (5) is an equation with degenerate kernel $ f( x, y) = \alpha \cos \sqrt {\lambda _ {0} } x \cos \sqrt {\lambda _ {0} } y $ | ||
| + | and its solution is | ||
| − | + | $$ | |
| + | K( x, y) = - | ||
| + | \frac{\alpha \cos \sqrt {\lambda _ {0} } x \cos \sqrt {\lambda _ {0} } y }{1 + \alpha \int\limits _ { 0 } ^ { x } \cos ^ {2} \sqrt {\lambda _ {0} } t dt } | ||
| + | . | ||
| + | $$ | ||
| − | + | Now the function $ q $ | |
| + | and the number $ h $ | ||
| + | are determined by the formulas | ||
| − | + | $$ | |
| + | q( x) = 2 | ||
| + | \frac{dK( x, x) }{dx} | ||
| + | = - 2 | ||
| + | \frac{d}{dx} | ||
| + | \left ( | ||
| + | \frac{\alpha \ | ||
| + | \cos ^ {2} \sqrt { | ||
| + | \lambda _ {0} } x }{1 + \alpha \int\limits _ { 0 } ^ { x } \cos ^ {2} \sqrt {\lambda _ {0} } t dt } | ||
| + | \right ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | h = K( 0, 0) = - \alpha . | ||
| + | $$ | ||
| + | |||
| + | $ 2 $. | ||
| + | Let a real-valued function $ q $ | ||
| + | satisfy the inequality | ||
| + | |||
| + | $$ \tag{6 } | ||
| + | \int\limits _ { 0 } ^ \infty x | q( x) | dx < \infty . | ||
| + | $$ | ||
Then the boundary value problem | Then the boundary value problem | ||
| − | + | $$ \tag{7 } | |
| + | - y ^ {\prime\prime} + q( x) y = \lambda ^ {2} y,\ \ | ||
| + | 0 < x < \infty , | ||
| + | $$ | ||
| − | + | $$ \tag{7'} | |
| + | y( 0) = 0, | ||
| + | $$ | ||
| − | has bounded solutions for | + | has bounded solutions for $ \lambda ^ {2} > 0 $ |
| + | and $ \lambda = i \lambda _ {k} $, | ||
| + | $ \lambda _ {k} > 0 $, | ||
| + | $ k = 1 \dots n $. | ||
| + | Moreover, these solutions satisfy for $ x \rightarrow \infty $ | ||
| + | the asymptotic formulas | ||
| − | + | $$ | |
| + | y( x, \lambda ) = e ^ {- i \lambda x } - S( \lambda ) e ^ {i \lambda x } + | ||
| + | o( 1),\ \ | ||
| + | 0 < \lambda ^ {2} < \infty , | ||
| + | $$ | ||
| − | + | $$ | |
| + | y( x, i \lambda _ {k} ) = m _ {k} e ^ {- \lambda _ {k} x } [ 1+ o( 1)] ,\ m _ {k} > 0,\ k = 1 \dots n. | ||
| + | $$ | ||
| − | Here | + | Here $ m _ {k} $ |
| + | is a normalization factor: $ \int _ {0} ^ \infty | y( x , i \lambda _ {k} ) | ^ {2} dx = 1 $. | ||
| + | The set of values $ \{ {S(\lambda) } : {-\infty<\lambda<\infty; \lambda _ {k} , m _ {k} ; k= 1\dots n } \} $ | ||
| + | is called the scattering data for the boundary value problem (7), (7'}). It is required to reconstruct the potential $ q $ | ||
| + | from the scattering data. | ||
| − | To solve this problem, a function | + | To solve this problem, a function $ F $ |
| + | is constructed by the formula | ||
| − | + | $$ | |
| + | F( x) = \sum_{k=1}^ { n } m _ {k} ^ {2} e ^ {- \lambda _ {k} x } + | ||
| + | \frac{1}{2 \pi } | ||
| + | \int\limits _ {- \infty } ^ \infty [ 1- S( \lambda )] e ^ {i \lambda x } d \lambda | ||
| + | $$ | ||
and one considers the following equation: | and one considers the following equation: | ||
| − | + | $$ \tag{8 } | |
| + | F( x+ y) + K( x, y) + \int\limits _ { x } ^ \infty K( x, t) F( t+ y) dt = 0. | ||
| + | $$ | ||
| − | This equation has a unique solution | + | This equation has a unique solution $ K( x, y) $ |
| + | for any $ x \geq 0 $. | ||
| + | After this equation has been solved, the potential $ q $ | ||
| + | is determined by the formula | ||
| − | + | $$ | |
| + | q( x) = - 2 | ||
| + | \frac{dK( x, x) }{dx} | ||
| + | . | ||
| + | $$ | ||
| − | For a set < | + | For a set $ \{ {S(\lambda) } : {-\infty<\lambda<\infty; \lambda _ {k} , m _ {k} ; \lambda _ {k} > 0, m _ {k} > 0, k= 1\dots n } \} $ |
| + | to be the scattering data for some boundary value problem of the form (7), (7'}) with a real potential $ q $ | ||
| + | which satisfies the condition (6), it is necessary and sufficient that the following conditions are satisfied (see [[#References|[1]]]): | ||
| − | a) the function | + | a) the function $ S( \lambda ) $ |
| + | is continuous on the whole line, $ \overline{ {S( \lambda ) }}\; = S(- \lambda ) = [ S( \lambda )] ^ {-1} $, | ||
| + | $ 1- S( \lambda ) $ | ||
| + | tends to zero as $ | \lambda | \rightarrow \infty $ | ||
| + | and is the Fourier transform of the function | ||
| − | + | $$ | |
| + | F _ {S} ( x) = | ||
| + | \frac{1}{2 \pi } | ||
| + | \int\limits _ {- \infty } ^ \infty [ 1- S( \lambda )] e ^ {i | ||
| + | \lambda x } d \lambda , | ||
| + | $$ | ||
| − | which is representable as a sum of two functions, one of which belongs to | + | which is representable as a sum of two functions, one of which belongs to $ L _ {1} (- \infty , \infty ) $, |
| + | while the second is bounded and belongs to $ L _ {2} (- \infty , \infty ) $. | ||
| + | On the half-line $ 0 < x < \infty $ | ||
| + | the function $ F _ {S} ( x) $ | ||
| + | has a derivative $ F _ {S} ^ { \prime } ( x) $ | ||
| + | satisfying the condition $ \int _ {0} ^ \infty x | F _ {S} ^ { \prime } ( x) | dx < \infty $; | ||
| − | b) the increment of the argument in the function | + | b) the increment of the argument in the function $ S( \lambda ) $ |
| + | is connected with the number $ n $ | ||
| + | of negative eigenvalues (i.e. of the numbers $ - \lambda _ {1} ^ {2} \dots - \lambda _ {n} ^ {2} $) | ||
| + | of the boundary value problem (7), (7'}) by the formula | ||
| − | + | $$ | |
| + | n = | ||
| + | \frac{ \mathop{\rm ln} S(+ 0) - \mathop{\rm ln} S(+ \infty ) }{2 \pi i } | ||
| + | - 1- S( | ||
| + | \frac{0)}{4} | ||
| + | . | ||
| + | $$ | ||
| − | The integral equation (8) for | + | The integral equation (8) for $ K( x, y) $ |
| + | has an explicit solution if $ S( \lambda ) $ | ||
| + | is a rational function. Solutions of the equation (7) and the potential $ q $ | ||
| + | are obtained in this case as rational functions in the trigonometric and hyperbolic functions. For example, if | ||
| − | + | $$ | |
| + | S ( \lambda ) = | ||
| + | \frac{( \lambda + i)( \lambda + 2i) }{( \lambda - i)( \lambda | ||
| + | - 2i) } | ||
| + | ,\ \ | ||
| + | \lambda _ {1} = 1,\ \ | ||
| + | m _ {1} = \sqrt 6 , | ||
| + | $$ | ||
then the corresponding potential has the form | then the corresponding potential has the form | ||
| − | + | $$ | |
| + | q( x) = - | ||
| + | \frac{24}{( 2 \cosh 2x- \sinh 2x) ^ {2} } | ||
| + | . | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Z.S. Agranovich, V.A. Marchenko, "The inverse problem in scattering theory" , Khar'kov (1960) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. Shadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.M. Levitan, "Generalized translation operators and some of their applications" , Israel Program Sci. Transl. (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> , ''The theory of solitons: methods of the inverse problem'' , Moscow (1980) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L.D. Faddeev, "The inverse problem in quantum scattering theory" ''Uspekhi Mat. Nauk'' , '''14''' : 4 (1959) pp. 57–119 (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.D. Faddeev, "Inverse problem of quantum scattering theory II" ''J. Soviet. Math.'' , '''5''' : 3 (1976) pp. 334–450 ''Itogi Nauk. i Tekhn. Sovremen. Probl. Mat.'' , '''3''' (1974) pp. 93–180</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> B.M. Levitan, M.G. Gasymov, "Determination of a differential equation by two of its spectra" ''Russian Math. Surveys'' , '''19''' : 2 (1964) pp. 1–64 ''Uspkehi Mat. Nauk'' , '''19''' : 2 (1964) pp. 3–63</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V. Ambarzumian, ''Z. Phys.'' , '''53''' (1929) pp. 690–695</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> G. Borg, "Eine Umkehrung der Sturm–Liouvilleschen Eigenwertaufgabe, Bestimmung der Differentialgleichung durch die Eigenwerte" ''Acta Math.'' , '''78''' (1946) pp. 1–96</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> N. Levinson, "On the uniqueness of the potential in a Schrödinger equation for a given asymptotic phase" ''Danske Vid. Selsk. Mat. -Fys. Medd.'' , '''25''' : 9 (1949) pp. 1–29</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> V.A. Marchenko, "On the theory of a second-order differential operator" ''Dokl. Akad. Nauk SSSR'' , '''72''' : 3 (1950) pp. 457–460 (In Russian)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> I.M. Gel'fand, B.M. Levitan, "On the determination of a differential equation from its spectral function" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''15''' : 4 (1951) pp. 309–360 (In Russian)</TD></TR><TR><TD valign="top">[15a]</TD> <TD valign="top"> M.G. Krein, "Solution of the inverse Sturm–Liouville problem" ''Dokl. Akad. Nauk SSSR'' , '''76''' : 1 (1951) pp. 21–24 (In Russian)</TD></TR><TR><TD valign="top">[15b]</TD> <TD valign="top"> M.G. Krein, "On inverse problems for a nonhomogeneous chord" ''Dokl. Akad. Nauk SSSR'' , '''82''' : 5 (1952) pp. 669–672 (In Russian)</TD></TR><TR><TD valign="top">[15c]</TD> <TD valign="top"> M.G. Krein, "On the transfer function of a one-dimensional second-order boundary problem" ''Dokl. Akad. Nauk SSSR'' , '''88''' : 3 (1953) pp. 405–408 (In Russian)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> V.A. Marchenko, "On reconstructing the potential energy from phases of scattered waves" ''Dokl. Akad. Nauk SSSR'' , '''104''' : 5 (1955) pp. 695–698 (In Russian)</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> B.Ya. Levin, "Transformations of Fourier and Laplace types by means of solutions of second-order differential equations" ''Dokl. Akad. Nauk SSSR'' , '''106''' : 2 (1956) pp. 187–190 (In Russian)</TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> R. Newton, R. Jost, "The construction of potentials from the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780135.png" />-matrix for systems of differential equations" ''Nuovo Cimento'' , '''1''' : 4 (1955) pp. 590–622</TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> M.G. Gasymov, B.M. Levitan, "Determination of Dirac's system from the scattering phase" ''Soviet Math. Dokl.'' , '''7''' : 2 (1966) pp. 543–547 ''Dokl. Akad. Nauk SSSR'' , '''167''' : 6 (1966) pp. 1219–1222</TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> M.G. Gasymov, "The inverse problem of scattering theory for a system of Dirac equations of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780136.png" />" ''Trudy Moskov. Mat. Obshch.'' , '''19''' (1968) pp. 41–112 (In Russian)</TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> F.S. Rofe-Beketov, "The spectral matrix and the inverse Sturm–Liouville problem on the axis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780137.png" />" ''Teor. Funktsii, Funktional. Analiz. i Prilozhen.'' : 4 (1967) pp. 189–197 (In Russian)</TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> B.M. Levitan, "The inverse problem in quantum scattering theory at fixed energy" , ''Probl. Mekh. i Mat. Fiz. (I.G. Petrovskii)'' , Moscow (1976) pp. 166–207 (In Russian)</TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> N.I. Akhiezer, "A continuous analogue of orthogonal polynomials on a system of intervals" ''Soviet Math. Dokl.'' , '''2''' : 6 (1961) pp. 1409–1412 ''Dokl. Akad. SSSR'' , '''141''' : 2 (1961) pp. 263–266</TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> G.Sh. Guseinov, "The inverse problem of scattering theory for a second-order difference equation on the whole axis" ''Soviet Math. Dokl.'' , '''17''' : 6 (1976) pp. 1684–1688 ''Dokl. Akad. Nauk SSSR'' , '''231''' : 5 (1976) pp. 1045–1048</TD></TR><TR><TD valign="top">[25]</TD> <TD valign="top"> B.M. Levitan, "Inverse Sturm–Liouville problems" , VNU (1987) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Z.S. Agranovich, V.A. Marchenko, "The inverse problem in scattering theory" , Khar'kov (1960) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. Shadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.M. Levitan, "Generalized translation operators and some of their applications" , Israel Program Sci. Transl. (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> , ''The theory of solitons: methods of the inverse problem'' , Moscow (1980) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L.D. Faddeev, "The inverse problem in quantum scattering theory" ''Uspekhi Mat. Nauk'' , '''14''' : 4 (1959) pp. 57–119 (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.D. Faddeev, "Inverse problem of quantum scattering theory II" ''J. Soviet. Math.'' , '''5''' : 3 (1976) pp. 334–450 ''Itogi Nauk. i Tekhn. Sovremen. Probl. Mat.'' , '''3''' (1974) pp. 93–180</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> B.M. Levitan, M.G. Gasymov, "Determination of a differential equation by two of its spectra" ''Russian Math. Surveys'' , '''19''' : 2 (1964) pp. 1–64 ''Uspkehi Mat. Nauk'' , '''19''' : 2 (1964) pp. 3–63</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V. Ambarzumian, ''Z. Phys.'' , '''53''' (1929) pp. 690–695</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> G. Borg, "Eine Umkehrung der Sturm–Liouvilleschen Eigenwertaufgabe, Bestimmung der Differentialgleichung durch die Eigenwerte" ''Acta Math.'' , '''78''' (1946) pp. 1–96</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> N. Levinson, "On the uniqueness of the potential in a Schrödinger equation for a given asymptotic phase" ''Danske Vid. Selsk. Mat. -Fys. Medd.'' , '''25''' : 9 (1949) pp. 1–29</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> V.A. Marchenko, "On the theory of a second-order differential operator" ''Dokl. Akad. Nauk SSSR'' , '''72''' : 3 (1950) pp. 457–460 (In Russian)</TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> I.M. Gel'fand, B.M. Levitan, "On the determination of a differential equation from its spectral function" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''15''' : 4 (1951) pp. 309–360 (In Russian)</TD></TR><TR><TD valign="top">[15a]</TD> <TD valign="top"> M.G. Krein, "Solution of the inverse Sturm–Liouville problem" ''Dokl. Akad. Nauk SSSR'' , '''76''' : 1 (1951) pp. 21–24 (In Russian)</TD></TR><TR><TD valign="top">[15b]</TD> <TD valign="top"> M.G. Krein, "On inverse problems for a nonhomogeneous chord" ''Dokl. Akad. Nauk SSSR'' , '''82''' : 5 (1952) pp. 669–672 (In Russian)</TD></TR><TR><TD valign="top">[15c]</TD> <TD valign="top"> M.G. Krein, "On the transfer function of a one-dimensional second-order boundary problem" ''Dokl. Akad. Nauk SSSR'' , '''88''' : 3 (1953) pp. 405–408 (In Russian)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> V.A. Marchenko, "On reconstructing the potential energy from phases of scattered waves" ''Dokl. Akad. Nauk SSSR'' , '''104''' : 5 (1955) pp. 695–698 (In Russian)</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> B.Ya. Levin, "Transformations of Fourier and Laplace types by means of solutions of second-order differential equations" ''Dokl. Akad. Nauk SSSR'' , '''106''' : 2 (1956) pp. 187–190 (In Russian)</TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> R. Newton, R. Jost, "The construction of potentials from the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780135.png" />-matrix for systems of differential equations" ''Nuovo Cimento'' , '''1''' : 4 (1955) pp. 590–622</TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> M.G. Gasymov, B.M. Levitan, "Determination of Dirac's system from the scattering phase" ''Soviet Math. Dokl.'' , '''7''' : 2 (1966) pp. 543–547 ''Dokl. Akad. Nauk SSSR'' , '''167''' : 6 (1966) pp. 1219–1222</TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> M.G. Gasymov, "The inverse problem of scattering theory for a system of Dirac equations of order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780136.png" />" ''Trudy Moskov. Mat. Obshch.'' , '''19''' (1968) pp. 41–112 (In Russian)</TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> F.S. Rofe-Beketov, "The spectral matrix and the inverse Sturm–Liouville problem on the axis <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780137.png" />" ''Teor. Funktsii, Funktional. Analiz. i Prilozhen.'' : 4 (1967) pp. 189–197 (In Russian)</TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> B.M. Levitan, "The inverse problem in quantum scattering theory at fixed energy" , ''Probl. Mekh. i Mat. Fiz. (I.G. Petrovskii)'' , Moscow (1976) pp. 166–207 (In Russian)</TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> N.I. Akhiezer, "A continuous analogue of orthogonal polynomials on a system of intervals" ''Soviet Math. Dokl.'' , '''2''' : 6 (1961) pp. 1409–1412 ''Dokl. Akad. SSSR'' , '''141''' : 2 (1961) pp. 263–266</TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> G.Sh. Guseinov, "The inverse problem of scattering theory for a second-order difference equation on the whole axis" ''Soviet Math. Dokl.'' , '''17''' : 6 (1976) pp. 1684–1688 ''Dokl. Akad. Nauk SSSR'' , '''231''' : 5 (1976) pp. 1045–1048</TD></TR><TR><TD valign="top">[25]</TD> <TD valign="top"> B.M. Levitan, "Inverse Sturm–Liouville problems" , VNU (1987) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The inverse problem for the Schrödinger operator | + | The inverse problem for the Schrödinger operator $ - ( {d ^ {2} } / {dx ^ {2} } ) + q( x) $, |
| + | $ - \infty < x < + \infty $, | ||
| + | has been investigated in [[#References|[a1]]]. (See also [[Schrödinger equation|Schrödinger equation]].) In order to derive necessary and sufficient conditions in the scattering data to correspond with the equation $ - y ^ {\prime\prime} + q( x) y= \lambda ^ {2} y $, | ||
| + | $ - \infty < x< \infty $, | ||
| + | it is assumed in [[#References|[a1]]] that $ q $ | ||
| + | satisfies $ \int _ {- \infty } ^ {+ \infty } | q( x) | ( 1+ x ^ {2} ) dx < \infty $, | ||
| + | cf. [[#References|[6]]]. The condition on the Fourier transforms $ F _ {i} $, | ||
| + | are analogous to $ F _ {S} $, | ||
| + | defined above is also changed: $ \int _ {a} ^ \infty | F _ {1} ^ { \prime } ( x) | dx $, | ||
| + | $ \int _ {- \infty } ^ {a} | F _ {2} ^ { \prime } ( x) | ( 1+ x ^ {2} ) dx < \infty $ | ||
| + | for all $ - \infty < a < + \infty $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Deift, E. Trubowitz, "Inverse scattering on the line" ''Comm. Pure Appl. Math.'' , '''32''' (1979) pp. 121–251</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Pöschel, E. Trubowitz, "Inverse spectral theory" , Acad. Press (1987)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.G. Ramm, "Inverse scattering on half-line" ''J. Math. Anal. Appl.'' , '''133''' (1988) pp. 543–572</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.G. Ramm, B.A. Taylor, "Example of a potential in one-dimensional scattering problem for which there are infinitely many purely imaginary resonances" ''Phys. Lett.'' , '''124A''' (1987) pp. 313–319</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L.E. Andersson, "Inverse eigenvalue problems with discontinuous coefficients" ''Inverse Probl.'' , '''4''' (1988) pp. 353–397</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A.G. Ramm, "Recovery of the potential from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780149.png" />-function" ''Math. Reports Canad. Acad. Sci.'' , '''9''' (1987) pp. 177–182</TD></TR><TR><TD valign="top">[a7a]</TD> <TD valign="top"> A.G. Ramm, "Necessary and sufficient conditions on the scattering data for the potential to be in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780150.png" /> for the Schrödinger operator on the half-line" ''Inverse Probl.'' , '''3''' (1987) pp. L71–76</TD></TR><TR><TD valign="top">[a7b]</TD> <TD valign="top"> A.G. Ramm, "An inverse problem for the Helmholtz equation in a semi-infinite medium" ''Inverse Probl.'' , '''3''' (1987) pp. L19–22</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> E.L. Isaacson, E. Trubowitz, "The inverse Sturm–Liouville problem I" ''Comm. Pure Appl. Math.'' , '''36''' (1983) pp. 767–784</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E.L. Isaacson, H.P. McKean, E. Trubowitz, "The inverse Sturm–Liouville problem II" ''Comm. Pure Appl. Math.'' , '''37''' (1984) pp. 1–12</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> B.E.J. Dahlberg, E. Trubowitz, "The inverse Sturm–Liouville problem III" ''Comm. Pure Appl. Math.'' , '''37''' (1984) pp. 255–267</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Deift, E. Trubowitz, "Inverse scattering on the line" ''Comm. Pure Appl. Math.'' , '''32''' (1979) pp. 121–251</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Pöschel, E. Trubowitz, "Inverse spectral theory" , Acad. Press (1987)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.G. Ramm, "Inverse scattering on half-line" ''J. Math. Anal. Appl.'' , '''133''' (1988) pp. 543–572</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.G. Ramm, B.A. Taylor, "Example of a potential in one-dimensional scattering problem for which there are infinitely many purely imaginary resonances" ''Phys. Lett.'' , '''124A''' (1987) pp. 313–319</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> L.E. Andersson, "Inverse eigenvalue problems with discontinuous coefficients" ''Inverse Probl.'' , '''4''' (1988) pp. 353–397</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A.G. Ramm, "Recovery of the potential from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780149.png" />-function" ''Math. Reports Canad. Acad. Sci.'' , '''9''' (1987) pp. 177–182</TD></TR><TR><TD valign="top">[a7a]</TD> <TD valign="top"> A.G. Ramm, "Necessary and sufficient conditions on the scattering data for the potential to be in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090780/s090780150.png" /> for the Schrödinger operator on the half-line" ''Inverse Probl.'' , '''3''' (1987) pp. L71–76</TD></TR><TR><TD valign="top">[a7b]</TD> <TD valign="top"> A.G. Ramm, "An inverse problem for the Helmholtz equation in a semi-infinite medium" ''Inverse Probl.'' , '''3''' (1987) pp. L19–22</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> E.L. Isaacson, E. Trubowitz, "The inverse Sturm–Liouville problem I" ''Comm. Pure Appl. Math.'' , '''36''' (1983) pp. 767–784</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E.L. Isaacson, H.P. McKean, E. Trubowitz, "The inverse Sturm–Liouville problem II" ''Comm. Pure Appl. Math.'' , '''37''' (1984) pp. 1–12</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> B.E.J. Dahlberg, E. Trubowitz, "The inverse Sturm–Liouville problem III" ''Comm. Pure Appl. Math.'' , '''37''' (1984) pp. 255–267</TD></TR></table> | ||
Latest revision as of 13:01, 13 January 2024
A problem in which it is required to reconstruct a function (a potential) $ q $
from some spectral characteristics of the operator $ A $
generated by the differential expression $ l[ y] = - y ^ {\prime\prime} + q( x) y $
and some boundary conditions in the Hilbert space $ L _ {2} ( a, b) $,
where $ x $
varies in a finite or infinite interval $ ( a, b) $.
Moreover, one should also reconstruct the boundary conditions corresponding to the operator $ A $.
When studying inverse problems, the following natural questions arise: 1) to find out which spectral characteristics determine the operator $ A $ uniquely; 2) to give a method of reconstructing the operator $ A $ from these spectral characteristics; and 3) to find particular properties of the spectral characteristics considered. Depending on the choice of the spectral characteristics, different statements of inverse problems are possible (often arising in applications).
The first result concerning inverse problems (see [10]), which gave a start to the whole theory, is: Let $ \lambda _ {0} , \lambda _ {1} \dots $ be the eigenvalues for the problem
$$ \tag{1 } \left . \begin{array}{c} - y ^ {\prime\prime} + q( x) y = \lambda y ,\ 0 \leq x \leq \pi , \\ y ^ \prime ( 0) = y ^ \prime ( \pi ) = 0, \\ \end{array} \right \} $$
and let $ q $ be a real-valued continuous function on the interval $ [ 0, \pi ] $. If $ \lambda _ {n} = n ^ {2} $, $ n = 0, 1 \dots $ then $ q( x) \equiv 0 $.
A profound study of inverse problems started in the 1940's (see [11], [12]). Let $ \lambda _ {0} , \lambda _ {1} \dots $ be the eigenvalues for the equation (1) under the boundary conditions
$$ \tag{2 } y ^ \prime ( 0) - hy( 0) = 0,\ \ y ^ \prime ( \pi ) + Hy( \pi ) = 0 $$
( $ h $ and $ H $ are real numbers), and let $ \mu _ {0} , \mu _ {1} \dots $ be the eigenvalues of (1) under the boundary conditions
$$ y ^ \prime ( 0) - h _ {1} y( 0) = 0,\ \ y ^ \prime ( \pi ) + Hy( \pi ) = 0 ,\ \ h _ {1} \neq h. $$
Then the sequences $ \{ \lambda _ {n} \} $ and $ \{ \mu _ {n} \} $, $ n = 0, 1 \dots $ determine the function $ q $ and the numbers $ h $, $ h _ {1} $ and $ H $ uniquely. Moreover, if at least one eigenvalue in these problems has not been determined, then all the others do not determine the equation (1) uniquely. In particular, generally speaking, one spectrum does not determine the equation uniquely (the above-mentioned result is an exception to the general rule).
If the equation (1) is studied on the half-line $ ( 0, \infty ) $ and the potential function $ q $ satisfies the requirement
$$ \int\limits _ { 0 } ^ \infty x | q( x) | dx < \infty , $$
then the solution $ \phi ( x, \lambda ) $ of the problem $ - y ^ {\prime\prime} + q( x) y = \lambda ^ {2} y $, $ y( 0) = 0 $, has an asymptotic representation for $ x \rightarrow \infty $,
$$ \phi ( x, \lambda ) = M( \lambda ) \sin [ \lambda x + \delta ( \lambda )] + o( 1). $$
The function $ \delta ( \lambda ) $ is called the scattering phase. The main result is that if a problem (considered in the space $ L _ {2} ( 0, \infty ) $) does not have discrete eigenvalues, then the scattering phase determines the potential function $ q $ uniquely.
A decisive step in the further development of the theory of inverse problems was the application of so-called operator-transform techniques (see Sturm–Liouville equation), which was naturally developed in the framework of the theory of generalized shift operators (see [4]).
Applying operator transforms to inverse problems (see [13]) allowed one to generalize the above-mentioned theorems. Namely, it turned out that the most general inverse problem is the problem of reconstructing equation (1) from its spectral function (see Sturm–Liouville problem). It was shown that the spectral function determines this equation uniquely. Moreover, it is of no importance whether the considered interval is finite or infinite.
In principle, all inverse problems can be reduced to the inverse problem of reconstructing an operator from its spectral function. However, this way is not always the simplest; moreover, when following it, one often encounters difficulties in finding necessary and sufficient conditions for the spectral characteristics that are used to reconstruct the operator.
The significance of inverse problems became greater after discovering a possibility to apply them to solve some non-linear evolution equations of mathematical physics. In particular, a relationship (see [25]) between inverse problems for some Sturm–Liouville operators with a finite number of gaps in the spectrum and the Jacobi inversion problem for Abelian integrals was established. Recent development of these ideas made it possible to obtain explicit formulas, which express finite gap potentials by Riemann $ \theta $- functions (see [1], [5]).
Below two versions of the statement and solution of inverse problems will be considered.
$ 1 $. Given a known spectral function $ \rho ( \lambda ) $, find a differential equation in the form
$$ l[ y] = - y ^ {\prime\prime} + q( x) y $$
with a real locally-summable potential $ q( x) $, $ 0 \leq x < \infty $, and a number $ h $ appearing in the boundary condition
$$ \tag{3 } y ^ \prime ( 0) - hy( 0) = 0. $$
To solve this problem it is assumed that
$$ \tag{4 } \Phi ( x) = \int\limits _ {- \infty } ^ { + \infty } \frac{1 - \cos \sqrt \lambda x } \lambda d \rho ( \lambda ),\ \ 0 < x < \infty , $$
$$ f( x, y) = \frac{1}{2} \{ \Phi ^ {\prime\prime} ( x+ y) + \Phi ^ {\prime\prime} ( | x- y | ) \} . $$
It turns out that the integral equation
$$ \tag{5 } f( x, y) + K( x, y) + \int\limits _ { 0 } ^ { x } K( x, t) f( t, y) dt = 0,\ \ 0 \leq y \leq x, $$
has a unique solution $ K( x, y) $ for each fixed $ x $. The potential $ q $ is defined by the formula
$$ q( x) = 2 \frac{dK( x, x) }{dx} , $$
and the number $ h $ in (3) is given by the formula $ h = K( 0, 0) $( see [14]). The solution $ \phi ( x, y) $ of the equation $ l [ y] = \lambda y $ and satisfying the boundary conditions $ \phi ( 0, \lambda ) = 1 $ and $ \phi ^ \prime ( 0, \lambda ) = h $ can be found by the formula
$$ \phi ( x, \lambda ) = \cos \sqrt \lambda x + \int\limits _ { 0 } ^ { x } K( x, t) \ \cos \sqrt \lambda t dt. $$
Further, a non-decreasing function $ \rho ( \lambda ) $, $ - \infty < \lambda < \infty $, is the spectral function for some problem $ - y ^ {\prime\prime} + q( x) y = \lambda y $, $ 0 \leq x < \infty $, $ y ^ \prime ( 0) - hy( 0) = 0 $, where $ q $ is a real-valued function with $ m $ locally-summable derivatives and $ h $ is a real number, if and only if the function $ \Phi ( x) $ constructed from $ \rho ( \lambda ) $ by formula (4) has $ m+ 3 $ locally-summable derivatives and $ \Phi ^ {\prime\prime} (+ 0) = - h $( see [14], [17], [9]). In a number of particular cases, $ q $ and $ h $ can be found effectively from the function $ \rho ( \lambda ) $. For example, let
$$ \rho ( \lambda ) = \left \{ \begin{array}{lll} \frac{2} \pi \sqrt \lambda + \alpha \chi ( \lambda - \lambda _ {0} ) & \textrm{ for } &\lambda > 0, \\ \alpha \chi ( \lambda - \lambda _ {0} ) & \textrm{ for } &\lambda < 0, \\ \end{array} \right .$$
where $ \chi ( \lambda ) = 0 $ for $ \lambda < 0 $ and $ \chi ( \lambda ) = 1 $ for $ \lambda > 0 $ and $ \alpha $ is a positive number. In this case the integral equation (5) is an equation with degenerate kernel $ f( x, y) = \alpha \cos \sqrt {\lambda _ {0} } x \cos \sqrt {\lambda _ {0} } y $ and its solution is
$$ K( x, y) = - \frac{\alpha \cos \sqrt {\lambda _ {0} } x \cos \sqrt {\lambda _ {0} } y }{1 + \alpha \int\limits _ { 0 } ^ { x } \cos ^ {2} \sqrt {\lambda _ {0} } t dt } . $$
Now the function $ q $ and the number $ h $ are determined by the formulas
$$ q( x) = 2 \frac{dK( x, x) }{dx} = - 2 \frac{d}{dx} \left ( \frac{\alpha \ \cos ^ {2} \sqrt { \lambda _ {0} } x }{1 + \alpha \int\limits _ { 0 } ^ { x } \cos ^ {2} \sqrt {\lambda _ {0} } t dt } \right ) , $$
$$ h = K( 0, 0) = - \alpha . $$
$ 2 $. Let a real-valued function $ q $ satisfy the inequality
$$ \tag{6 } \int\limits _ { 0 } ^ \infty x | q( x) | dx < \infty . $$
Then the boundary value problem
$$ \tag{7 } - y ^ {\prime\prime} + q( x) y = \lambda ^ {2} y,\ \ 0 < x < \infty , $$
$$ \tag{7'} y( 0) = 0, $$
has bounded solutions for $ \lambda ^ {2} > 0 $ and $ \lambda = i \lambda _ {k} $, $ \lambda _ {k} > 0 $, $ k = 1 \dots n $. Moreover, these solutions satisfy for $ x \rightarrow \infty $ the asymptotic formulas
$$ y( x, \lambda ) = e ^ {- i \lambda x } - S( \lambda ) e ^ {i \lambda x } + o( 1),\ \ 0 < \lambda ^ {2} < \infty , $$
$$ y( x, i \lambda _ {k} ) = m _ {k} e ^ {- \lambda _ {k} x } [ 1+ o( 1)] ,\ m _ {k} > 0,\ k = 1 \dots n. $$
Here $ m _ {k} $ is a normalization factor: $ \int _ {0} ^ \infty | y( x , i \lambda _ {k} ) | ^ {2} dx = 1 $. The set of values $ \{ {S(\lambda) } : {-\infty<\lambda<\infty; \lambda _ {k} , m _ {k} ; k= 1\dots n } \} $ is called the scattering data for the boundary value problem (7), (7'}). It is required to reconstruct the potential $ q $ from the scattering data.
To solve this problem, a function $ F $ is constructed by the formula
$$ F( x) = \sum_{k=1}^ { n } m _ {k} ^ {2} e ^ {- \lambda _ {k} x } + \frac{1}{2 \pi } \int\limits _ {- \infty } ^ \infty [ 1- S( \lambda )] e ^ {i \lambda x } d \lambda $$
and one considers the following equation:
$$ \tag{8 } F( x+ y) + K( x, y) + \int\limits _ { x } ^ \infty K( x, t) F( t+ y) dt = 0. $$
This equation has a unique solution $ K( x, y) $ for any $ x \geq 0 $. After this equation has been solved, the potential $ q $ is determined by the formula
$$ q( x) = - 2 \frac{dK( x, x) }{dx} . $$
For a set $ \{ {S(\lambda) } : {-\infty<\lambda<\infty; \lambda _ {k} , m _ {k} ; \lambda _ {k} > 0, m _ {k} > 0, k= 1\dots n } \} $ to be the scattering data for some boundary value problem of the form (7), (7'}) with a real potential $ q $ which satisfies the condition (6), it is necessary and sufficient that the following conditions are satisfied (see [1]):
a) the function $ S( \lambda ) $ is continuous on the whole line, $ \overline{ {S( \lambda ) }}\; = S(- \lambda ) = [ S( \lambda )] ^ {-1} $, $ 1- S( \lambda ) $ tends to zero as $ | \lambda | \rightarrow \infty $ and is the Fourier transform of the function
$$ F _ {S} ( x) = \frac{1}{2 \pi } \int\limits _ {- \infty } ^ \infty [ 1- S( \lambda )] e ^ {i \lambda x } d \lambda , $$
which is representable as a sum of two functions, one of which belongs to $ L _ {1} (- \infty , \infty ) $, while the second is bounded and belongs to $ L _ {2} (- \infty , \infty ) $. On the half-line $ 0 < x < \infty $ the function $ F _ {S} ( x) $ has a derivative $ F _ {S} ^ { \prime } ( x) $ satisfying the condition $ \int _ {0} ^ \infty x | F _ {S} ^ { \prime } ( x) | dx < \infty $;
b) the increment of the argument in the function $ S( \lambda ) $ is connected with the number $ n $ of negative eigenvalues (i.e. of the numbers $ - \lambda _ {1} ^ {2} \dots - \lambda _ {n} ^ {2} $) of the boundary value problem (7), (7'}) by the formula
$$ n = \frac{ \mathop{\rm ln} S(+ 0) - \mathop{\rm ln} S(+ \infty ) }{2 \pi i } - 1- S( \frac{0)}{4} . $$
The integral equation (8) for $ K( x, y) $ has an explicit solution if $ S( \lambda ) $ is a rational function. Solutions of the equation (7) and the potential $ q $ are obtained in this case as rational functions in the trigonometric and hyperbolic functions. For example, if
$$ S ( \lambda ) = \frac{( \lambda + i)( \lambda + 2i) }{( \lambda - i)( \lambda - 2i) } ,\ \ \lambda _ {1} = 1,\ \ m _ {1} = \sqrt 6 , $$
then the corresponding potential has the form
$$ q( x) = - \frac{24}{( 2 \cosh 2x- \sinh 2x) ^ {2} } . $$
References
| [1] | V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian) |
| [2] | Z.S. Agranovich, V.A. Marchenko, "The inverse problem in scattering theory" , Khar'kov (1960) (In Russian) |
| [3] | C. Shadan, P. Sabatier, "Inverse problems in quantum scattering theory" , Springer (1989) |
| [4] | B.M. Levitan, "Generalized translation operators and some of their applications" , Israel Program Sci. Transl. (1964) (Translated from Russian) |
| [5] | , The theory of solitons: methods of the inverse problem , Moscow (1980) (In Russian) |
| [6] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [7] | L.D. Faddeev, "The inverse problem in quantum scattering theory" Uspekhi Mat. Nauk , 14 : 4 (1959) pp. 57–119 (In Russian) |
| [8] | L.D. Faddeev, "Inverse problem of quantum scattering theory II" J. Soviet. Math. , 5 : 3 (1976) pp. 334–450 Itogi Nauk. i Tekhn. Sovremen. Probl. Mat. , 3 (1974) pp. 93–180 |
| [9] | B.M. Levitan, M.G. Gasymov, "Determination of a differential equation by two of its spectra" Russian Math. Surveys , 19 : 2 (1964) pp. 1–64 Uspkehi Mat. Nauk , 19 : 2 (1964) pp. 3–63 |
| [10] | V. Ambarzumian, Z. Phys. , 53 (1929) pp. 690–695 |
| [11] | G. Borg, "Eine Umkehrung der Sturm–Liouvilleschen Eigenwertaufgabe, Bestimmung der Differentialgleichung durch die Eigenwerte" Acta Math. , 78 (1946) pp. 1–96 |
| [12] | N. Levinson, "On the uniqueness of the potential in a Schrödinger equation for a given asymptotic phase" Danske Vid. Selsk. Mat. -Fys. Medd. , 25 : 9 (1949) pp. 1–29 |
| [13] | V.A. Marchenko, "On the theory of a second-order differential operator" Dokl. Akad. Nauk SSSR , 72 : 3 (1950) pp. 457–460 (In Russian) |
| [14] | I.M. Gel'fand, B.M. Levitan, "On the determination of a differential equation from its spectral function" Izv. Akad. Nauk SSSR Ser. Mat. , 15 : 4 (1951) pp. 309–360 (In Russian) |
| [15a] | M.G. Krein, "Solution of the inverse Sturm–Liouville problem" Dokl. Akad. Nauk SSSR , 76 : 1 (1951) pp. 21–24 (In Russian) |
| [15b] | M.G. Krein, "On inverse problems for a nonhomogeneous chord" Dokl. Akad. Nauk SSSR , 82 : 5 (1952) pp. 669–672 (In Russian) |
| [15c] | M.G. Krein, "On the transfer function of a one-dimensional second-order boundary problem" Dokl. Akad. Nauk SSSR , 88 : 3 (1953) pp. 405–408 (In Russian) |
| [16] | V.A. Marchenko, "On reconstructing the potential energy from phases of scattered waves" Dokl. Akad. Nauk SSSR , 104 : 5 (1955) pp. 695–698 (In Russian) |
| [17] | B.Ya. Levin, "Transformations of Fourier and Laplace types by means of solutions of second-order differential equations" Dokl. Akad. Nauk SSSR , 106 : 2 (1956) pp. 187–190 (In Russian) |
| [18] | R. Newton, R. Jost, "The construction of potentials from the 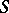 -matrix for systems of differential equations" Nuovo Cimento , 1 : 4 (1955) pp. 590–622 -matrix for systems of differential equations" Nuovo Cimento , 1 : 4 (1955) pp. 590–622 |
| [19] | M.G. Gasymov, B.M. Levitan, "Determination of Dirac's system from the scattering phase" Soviet Math. Dokl. , 7 : 2 (1966) pp. 543–547 Dokl. Akad. Nauk SSSR , 167 : 6 (1966) pp. 1219–1222 |
| [20] | M.G. Gasymov, "The inverse problem of scattering theory for a system of Dirac equations of order  " Trudy Moskov. Mat. Obshch. , 19 (1968) pp. 41–112 (In Russian) " Trudy Moskov. Mat. Obshch. , 19 (1968) pp. 41–112 (In Russian) |
| [21] | F.S. Rofe-Beketov, "The spectral matrix and the inverse Sturm–Liouville problem on the axis 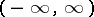 " Teor. Funktsii, Funktional. Analiz. i Prilozhen. : 4 (1967) pp. 189–197 (In Russian) " Teor. Funktsii, Funktional. Analiz. i Prilozhen. : 4 (1967) pp. 189–197 (In Russian) |
| [22] | B.M. Levitan, "The inverse problem in quantum scattering theory at fixed energy" , Probl. Mekh. i Mat. Fiz. (I.G. Petrovskii) , Moscow (1976) pp. 166–207 (In Russian) |
| [23] | N.I. Akhiezer, "A continuous analogue of orthogonal polynomials on a system of intervals" Soviet Math. Dokl. , 2 : 6 (1961) pp. 1409–1412 Dokl. Akad. SSSR , 141 : 2 (1961) pp. 263–266 |
| [24] | G.Sh. Guseinov, "The inverse problem of scattering theory for a second-order difference equation on the whole axis" Soviet Math. Dokl. , 17 : 6 (1976) pp. 1684–1688 Dokl. Akad. Nauk SSSR , 231 : 5 (1976) pp. 1045–1048 |
| [25] | B.M. Levitan, "Inverse Sturm–Liouville problems" , VNU (1987) (Translated from Russian) |
Comments
The inverse problem for the Schrödinger operator $ - ( {d ^ {2} } / {dx ^ {2} } ) + q( x) $, $ - \infty < x < + \infty $, has been investigated in [a1]. (See also Schrödinger equation.) In order to derive necessary and sufficient conditions in the scattering data to correspond with the equation $ - y ^ {\prime\prime} + q( x) y= \lambda ^ {2} y $, $ - \infty < x< \infty $, it is assumed in [a1] that $ q $ satisfies $ \int _ {- \infty } ^ {+ \infty } | q( x) | ( 1+ x ^ {2} ) dx < \infty $, cf. [6]. The condition on the Fourier transforms $ F _ {i} $, are analogous to $ F _ {S} $, defined above is also changed: $ \int _ {a} ^ \infty | F _ {1} ^ { \prime } ( x) | dx $, $ \int _ {- \infty } ^ {a} | F _ {2} ^ { \prime } ( x) | ( 1+ x ^ {2} ) dx < \infty $ for all $ - \infty < a < + \infty $.
References
| [a1] | P. Deift, E. Trubowitz, "Inverse scattering on the line" Comm. Pure Appl. Math. , 32 (1979) pp. 121–251 |
| [a2] | J. Pöschel, E. Trubowitz, "Inverse spectral theory" , Acad. Press (1987) |
| [a3] | A.G. Ramm, "Inverse scattering on half-line" J. Math. Anal. Appl. , 133 (1988) pp. 543–572 |
| [a4] | A.G. Ramm, B.A. Taylor, "Example of a potential in one-dimensional scattering problem for which there are infinitely many purely imaginary resonances" Phys. Lett. , 124A (1987) pp. 313–319 |
| [a5] | L.E. Andersson, "Inverse eigenvalue problems with discontinuous coefficients" Inverse Probl. , 4 (1988) pp. 353–397 |
| [a6] | A.G. Ramm, "Recovery of the potential from 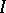 -function" Math. Reports Canad. Acad. Sci. , 9 (1987) pp. 177–182 -function" Math. Reports Canad. Acad. Sci. , 9 (1987) pp. 177–182 |
| [a7a] | A.G. Ramm, "Necessary and sufficient conditions on the scattering data for the potential to be in 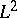 for the Schrödinger operator on the half-line" Inverse Probl. , 3 (1987) pp. L71–76 for the Schrödinger operator on the half-line" Inverse Probl. , 3 (1987) pp. L71–76 |
| [a7b] | A.G. Ramm, "An inverse problem for the Helmholtz equation in a semi-infinite medium" Inverse Probl. , 3 (1987) pp. L19–22 |
| [a8] | E.L. Isaacson, E. Trubowitz, "The inverse Sturm–Liouville problem I" Comm. Pure Appl. Math. , 36 (1983) pp. 767–784 |
| [a9] | E.L. Isaacson, H.P. McKean, E. Trubowitz, "The inverse Sturm–Liouville problem II" Comm. Pure Appl. Math. , 37 (1984) pp. 1–12 |
| [a10] | B.E.J. Dahlberg, E. Trubowitz, "The inverse Sturm–Liouville problem III" Comm. Pure Appl. Math. , 37 (1984) pp. 255–267 |
Sturm-Liouville problem, inverse. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sturm-Liouville_problem,_inverse&oldid=23059