Difference between revisions of "Jordan algebra"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (+ category) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | |||
| − | |||
| + | An [[Algebra|algebra]] in which the identities $$ | ||
| + | x y = y x , | ||
| + | ( x ^{2} y ) x = x ^{2} ( y x ) | ||
| + | $$ | ||
hold. Such algebras first arose in the paper [[#References|[1]]] of P. Jordan devoted to the axiomatic foundation of quantum mechanics (cf. also [[#References|[2]]]), and later found application in algebra, analysis and geometry. | hold. Such algebras first arose in the paper [[#References|[1]]] of P. Jordan devoted to the axiomatic foundation of quantum mechanics (cf. also [[#References|[2]]]), and later found application in algebra, analysis and geometry. | ||
| − | Let | + | Let $ A $ |
| + | be an associative algebra over a field of characteristic $ \neq 2 $( | ||
| + | cf. also [[Associative rings and algebras|Associative rings and algebras]]). The set $ A $ | ||
| + | together with the operations of addition and Jordan multiplication $$ | ||
| + | a \circ b = | ||
| − | + | \frac{a b + b a}{2} | |
| − | forms the algebra | + | $$ |
| + | forms the algebra $ A ^{(+)} $, | ||
| + | which is a Jordan algebra. A Jordan algebra that is isomorphic to a subalgebra of $ A ^{(+)} $ | ||
| + | for some associative algebra $ A $ | ||
| + | is called special. The role of special algebras in the theory of Jordan algebras is in many respects analogous to the role of associative algebras in the theory of alternative algebras (cf. also [[Alternative rings and algebras|Alternative rings and algebras]]). At the basis of this analogy lies the theorem that every two-generated subalgebra of a Jordan algebra is special. (Every two-generated subalgebra of an alternative algebra is associative.) However, the class of special Jordan algebras is not a variety, i.e. it is not given by identities, since special Jordan algebras can have non-special homomorphic images. Nevertheless, identities of degree 8 or 9 have been found that are satisfied by every special Jordan algebra, but are not satisfied by some non-special algebra, while it has been proved that such identities of degree $ \leq 7 $ | ||
| + | do not exist. A necessary and sufficient condition on an algebra to be special is: A Jordan algebra is special if and only if it can be isomorphically imbedded in a Jordan algebra each countable subset of which lies in a subalgebra generated by two elements. | ||
===Examples.=== | ===Examples.=== | ||
| − | 1) Let | + | 1) Let $ V $ |
| + | be a vector space over a field with a symmetric bilinear form $ f ( x ,\ y ) $, | ||
| + | and let $ F \cdot e _{0} + V $ | ||
| + | be a space of one dimension higher, on which $$ | ||
| + | ( \alpha e _{0} + u ) ( \beta e _{0} + v ) = | ||
| + | [ \alpha \beta + f ( u ,\ v ) ] | ||
| + | e _{0} + \alpha v + \beta u | ||
| + | $$ | ||
| + | determines the multiplication ( $ \alpha ,\ \beta \in F $; | ||
| + | $ u ,\ v \in V $). | ||
| + | The algebra that arises is called the algebra with symmetric bilinear form $ f $. | ||
| + | It can be isomorphically imbedded in the algebra $ C ( V ,\ f \ ) ^{(+)} $, | ||
| + | where $ C ( V ,\ f \ ) $ | ||
| + | is the [[Clifford algebra|Clifford algebra]] of $ f $, | ||
| + | and is therefore a special Jordan algebra. | ||
| − | + | 2) Let $ A $ | |
| + | be an associative algebra and $ j $ | ||
| + | an involution of it (an anti-isomorphism of order two). The set $$ | ||
| + | H ( A ,\ j ) = \{ {a \in A} : {a ^{j} = a} \} | ||
| + | $$ | ||
| + | is a subalgebra in $ A ^{(+)} $ | ||
| + | and is also a special Jordan algebra. | ||
| − | + | 3) Let $ C $ | |
| − | + | be an alternative non-associative algebra over a field $ F $ | |
| − | + | with involution $ c \mapsto \overline{c} $ | |
| + | whose fixed elements lie in the associative centre of $ C $. | ||
| + | In the algebra $ C _{3} $ | ||
| + | of matrices over $ C $ | ||
| + | of order 3, the set $$ | ||
| + | H ( C _{3} ,\ \Gamma ) = | ||
| + | \{ {X \in C _{3}} : {X = \Gamma ^{-1} \overline{X} {} ^ \prime \Gamma} \} | ||
| + | , | ||
| + | $$ | ||
| + | where $$ | ||
| + | \Gamma = | ||
| + | \mathop{\rm diag}\nolimits \{ \gamma _{1} ,\ \gamma _{2} ,\ \gamma _{3} \} , | ||
| + | \gamma _{i} \neq 0 , | ||
| + | \gamma _{i} \in F , | ||
| + | $$ | ||
| + | is a non-special Jordan algebra under the operations of addition and Jordan multiplication. This algebra is not the homomorphic image of any special algebra. | ||
| − | + | The finite-dimensional simple Jordan algebras over an algebraically closed field $ F $ | |
| + | of characteristic $ \neq 2 $ | ||
| + | have been completely classified (cf. [[#References|[3]]]). The central simple finite-dimensional Jordan algebras split into five series. The series –(D) are infinite and consist of special algebras, (E) consists of a single non-special algebra: | ||
| − | + | $ F _{n} ^{(+)} $; | |
| − | |||
| − | + | (B) $ H ( F _{n} ,\ J _{1} ) $, | |
| + | where $ J _{1} : \ X \rightarrow X ^ \prime $; | ||
| − | |||
| − | + | (C) $ H ( F _{2n} ,\ J _{S} ) $, | |
| + | where $ J _{S} : \ X \rightarrow \overline{S} {} ^ \prime X ^ \prime S $, | ||
| + | $ S = \mathop{\rm diag}\nolimits \{ Q \dots Q \} $, | ||
| + | $$ | ||
| + | Q = \left ( | ||
| + | \begin{array}{ll} | ||
| + | 0 & 1 \\ | ||
| + | 1 & 0 \\ | ||
| + | \end{array} | ||
| + | \ \right ) ; | ||
| + | $$( | ||
| + | D) $ F \cdot e _{0} + V $ | ||
| + | — the algebras of symmetric non-degenerate bilinear forms; | ||
| − | is | + | (E) $ H ( C _{3} ,\ J _{1} ) $, |
| + | where $ C $ | ||
| + | is the [[Cayley–Dickson algebra|Cayley–Dickson algebra]] with the standard involution. This algebra is $ 27 $- | ||
| + | dimensional over $ F $. | ||
| − | |||
| − | + | In each finite-dimensional Jordan algebra $ J $ | |
| + | the radical (the largest nil radical) $ N $ | ||
| + | is involutory and the quotient algebra $ \overline{J} = J / N $ | ||
| + | is a finite direct sum of simple Jordan algebras. If $ \overline{J} $ | ||
| + | is separable, then $ J $ | ||
| + | has a decomposition $ J = N + W $ | ||
| + | into the sum of the radical and a semi-simple subalgebra $ W $ | ||
| + | that is isomorphic to $ \overline{J} $. | ||
| + | In the case of characteristic 0, all semi-simple terms $ W $ | ||
| + | are conjugate relative to automorphisms of a special kind (cf. [[#References|[3]]]). This is also true in characteristic $ p > 0 $ | ||
| + | if some restrictions are imposed on the algebra. | ||
| − | ( | + | A generalization of the theory of finite-dimensional Jordan algebras is the theory of Jordan algebras with the minimum condition for quadratic (inner) ideals (cf. [[#References|[3]]], [[#References|[4]]], [[#References|[5]]]). A quadratic ideal $ Q $ |
| + | of an algebra $ J $ | ||
| + | is a subspace for which $ \{ qx q \} \in Q $ | ||
| + | for all $ q \in Q $ | ||
| + | and $ x \in J $, | ||
| + | where $ \{ a b c \} = ( a b) c + ( b c ) a - ( c a ) b $ | ||
| + | is the triple Jordan product. If $ J $ | ||
| + | is a Jordan algebra with the minimum condition for quadratic ideals and $ R $ | ||
| + | is its quadratic radical (cf. [[Radical of rings and algebras|Radical of rings and algebras]]), then the quotient algebra $ J / R $ | ||
| + | is a finite direct sum of simple algebras, which have been described apart from the Jordan algebras with division. If $ J $ | ||
| + | is a special algebra, it has been proved that the radical $ R $ | ||
| + | is nilpotent and finite-dimensional. | ||
| − | ( | + | An algebraic special Jordan algebra (cf. also [[Algebraic algebra|Algebraic algebra]]) that satisfies a non-trivial (for special algebras) identity is locally finite-dimensional; a special Jordan nil algebra (cf. also [[Nil algebra|Nil algebra]]) with a non-trivial identity is locally nilpotent [[#References|[6]]]. In particular, a special algebraic Jordan (nil) algebra of bounded index is locally finite-dimensional (nilpotent). A finitely-generated solvable Jordan algebra is nilpotent; this is not true for special algebras in the general case. A Jordan $ \Phi $- |
| + | operator ring that is a finitely-generated $ \Phi $- | ||
| + | module with nilpotent generating elements, is nilpotent [[#References|[7]]]. | ||
| − | + | With each Jordan algebra one can in various ways associate a [[Lie algebra|Lie algebra]] (cf. [[#References|[3]]], [[#References|[8]]]). A number of theorems on Jordan algebras have been obtained from known theorems on Lie algebras. E.g., it has been proved that a semi-simple finite-dimensional Jordan algebra over an algebraically closed field of characteristic zero has a basis with integral structure constants. For the theory of Lie algebras this construction is also useful, since certain important classes of Lie algebras can be realized by it. E.g., the Lie algebra of derivations of the simple Lie algebra of type (E) is the exceptional simple Lie algebra $ F _{4} $, | |
| − | + | the algebra of linear transformations of this algebra that leave invariant some cubic form is the exceptional simple Lie algebra $ E _{6} $. | |
| − | + | All five exceptional Lie algebras of types $ G _{2} $, | |
| − | + | $ F _{4} $, | |
| − | + | $ E _{6} $, | |
| − | + | $ E _{7} $, | |
| − | + | $ E _{8} $ | |
| − | + | can be realized by another construction, associating to an alternative algebra of degree 2 and a Jordan algebra of degree 3 some Lie algebra. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | With each Jordan algebra one can in various ways associate a [[Lie algebra|Lie algebra]] (cf. [[#References|[3]]], [[#References|[8]]]). A number of theorems on Jordan algebras have been obtained from known theorems on Lie algebras. E.g., it has been proved that a semi-simple finite-dimensional Jordan algebra over an algebraically closed field of characteristic zero has a basis with integral structure constants. For the theory of Lie algebras this construction is also useful, since certain important classes of Lie algebras can be realized by it. E.g., the Lie algebra of derivations of the simple Lie algebra of type (E) is the exceptional simple Lie algebra | ||
It is, finally, interesting to note that some algebras arising in genetics are Jordan algebras [[#References|[10]]]. | It is, finally, interesting to note that some algebras arising in genetics are Jordan algebras [[#References|[10]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P. Jordan, "Ueber Verallgemeinerungsmöglichkeiten des Formalismus der Quantenmechanik" ''Nachr. Akad. Wiss. Göttingen. Math. Phys. Kl. I'' , '''41''' (1933) pp. 209–217 {{MR|}} {{ZBL|0007.08502}} {{ZBL|59.0796.02}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.G. Emch, "Algebraic methods in statistical mechanics and quantum field theory" , Wiley (1972) {{MR|}} {{ZBL|0235.46085}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Jacobson, "Structure and representations of Jordan algebras" , Amer. Math. Soc. (1968) {{MR|0251099}} {{ZBL|0218.17010}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> K. McCrimmon, "The radical of a Jordan algebra" ''Proc. Nat. Acad. Sci. USA'' , '''62''' : 3 (1969) pp. 671–678 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.M. Slin'ko, "On the Jacobson radical and absolute zero divisors of special Jordan algebras" ''Algebra and Logic'' , '''11''' : 6 (1972) pp. 396–402 ''Algebra i Logika'' , '''11''' : 6 (1972) pp. 711–724</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.I. Shirshov, "On some non-associative null rings and algebraic algebras" ''Mat. Sb.'' , '''41''' : 3 (1957) pp. 381–394 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.P. Shestakov, "Certain classes of noncommutative Jordan rings" ''Algebra and Logic'' , '''10''' : 4 (1971) pp. 252–280 ''Algebra i Logika'' , '''10''' : 4 (1971) pp. 407–448 {{MR|}} {{ZBL|0259.17001}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.D. Schafer, "An introduction to nonassociative algebras" , Acad. Press (1966) {{MR|0210757}} {{ZBL|0145.25601}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> S.R. Gordon, "An integral basis theorem for Jordan algebras" ''J. of Algebra'' , '''24''' (1973) pp. 258–282 {{MR|0308229}} {{ZBL|0253.17010}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> R.D. Schafer, "Structure of genetic algebras" ''Amer. J. Math.'' , '''71''' (1949) pp. 121–135 {{MR|0027751}} {{ZBL|0034.02004}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> M. Koecher, "An elementary approach to bounded symmetric domains" , Rice Univ. (1969) {{MR|0261032}} {{ZBL|0217.10901}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> A.M. Slin'ko, et al., "Jordan algebras" , '''1''' , Novosibirsk (1976) (In Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P. Jordan, "Ueber Verallgemeinerungsmöglichkeiten des Formalismus der Quantenmechanik" ''Nachr. Akad. Wiss. Göttingen. Math. Phys. Kl. I'' , '''41''' (1933) pp. 209–217 {{MR|}} {{ZBL|0007.08502}} {{ZBL|59.0796.02}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.G. Emch, "Algebraic methods in statistical mechanics and quantum field theory" , Wiley (1972) {{MR|}} {{ZBL|0235.46085}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Jacobson, "Structure and representations of Jordan algebras" , Amer. Math. Soc. (1968) {{MR|0251099}} {{ZBL|0218.17010}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> K. McCrimmon, "The radical of a Jordan algebra" ''Proc. Nat. Acad. Sci. USA'' , '''62''' : 3 (1969) pp. 671–678 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.M. Slin'ko, "On the Jacobson radical and absolute zero divisors of special Jordan algebras" ''Algebra and Logic'' , '''11''' : 6 (1972) pp. 396–402 ''Algebra i Logika'' , '''11''' : 6 (1972) pp. 711–724 {{MR|}} {{ZBL|0284.17009}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.I. Shirshov, "On some non-associative null rings and algebraic algebras" ''Mat. Sb.'' , '''41''' : 3 (1957) pp. 381–394 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.P. Shestakov, "Certain classes of noncommutative Jordan rings" ''Algebra and Logic'' , '''10''' : 4 (1971) pp. 252–280 ''Algebra i Logika'' , '''10''' : 4 (1971) pp. 407–448 {{MR|}} {{ZBL|0259.17001}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> R.D. Schafer, "An introduction to nonassociative algebras" , Acad. Press (1966) {{MR|0210757}} {{ZBL|0145.25601}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> S.R. Gordon, "An integral basis theorem for Jordan algebras" ''J. of Algebra'' , '''24''' (1973) pp. 258–282 {{MR|0308229}} {{ZBL|0253.17010}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> R.D. Schafer, "Structure of genetic algebras" ''Amer. J. Math.'' , '''71''' (1949) pp. 121–135 {{MR|0027751}} {{ZBL|0034.02004}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> M. Koecher, "An elementary approach to bounded symmetric domains" , Rice Univ. (1969) {{MR|0261032}} {{ZBL|0217.10901}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> A.M. Slin'ko, et al., "Jordan algebras" , '''1''' , Novosibirsk (1976) (In Russian) {{MR|}} {{ZBL|0405.17013}} {{ZBL|0343.17007}} </TD></TR></table> |
| Line 68: | Line 147: | ||
For Jordan algebras in genetics see also [[Genetic algebra|Genetic algebra]]. | For Jordan algebras in genetics see also [[Genetic algebra|Genetic algebra]]. | ||
| − | There exists a functor Kan [[#References|[a1]]], called the Kantor functor, which establishes an isomorphism between the category of Jordan algebras and the category of | + | There exists a functor Kan [[#References|[a1]]], called the Kantor functor, which establishes an isomorphism between the category of Jordan algebras and the category of $ \mathbf Z $- |
| + | graded Lie algebras of the form $ \mathfrak g = \mathfrak g _{-1} + \mathfrak g _{0} + \mathfrak g _{1} $ | ||
| + | with the following properties [[#References|[a2]]]: | ||
| + | |||
| + | a) if $ a \in \mathfrak g _{0} $ | ||
| + | or $ \mathfrak g _{1} $ | ||
| + | and $ [a,\ \mathfrak g _{-1} ] = 0 $, | ||
| + | then $ a = 0 $; | ||
| − | |||
| − | b) | + | b) $ \mathfrak g _{1} $ |
| + | contains an element $ p $ | ||
| + | such that $ \mathfrak g _{1} = [ \mathfrak g _{0} ,\ p] + kp $, | ||
| + | and $ [ \mathfrak g _{-1} ,\ p] $ | ||
| + | generates the subalgebra $ \mathfrak g _{0} $( | ||
| + | $ k $ | ||
| + | is the base field). | ||
| + | |||
| + | The construction of $ \mathop{\rm Kan}\nolimits ^{-1} $ | ||
| + | is very simple: $ \mathop{\rm Kan}\nolimits ^{-1} ( \mathfrak g ) = \mathfrak g _{-1} $ | ||
| + | with product $ a \cdot b = [[p,\ a],\ b] $. | ||
| − | |||
This construction was extended to the super-algebra case and used to classify simple finite-dimensional Jordan super-algebras [[#References|[a2]]]. | This construction was extended to the super-algebra case and used to classify simple finite-dimensional Jordan super-algebras [[#References|[a2]]]. | ||
| Line 80: | Line 174: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.L. Kantor, "Classification of irreducible transitively differential groups" ''Soviet Math. Dokl.'' , '''5''' (1964) pp. 1404–1407 ''Dokl. Akad. Nauk SSSR'' , '''158''' : 5 (1964) pp. 1271–1274 {{MR|175941}} {{ZBL|0286.17011}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.G. Kac, "Classification of simple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427091.png" />-graded Lie superalgebras and simple Jordan superalgebras" ''Comm. in Algebra'' , '''5''' : 13 (1977) pp. 1375–1400 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Braun, M. Koecher, "Jordan-algebren" , Springer (1966) {{MR|0204470}} {{ZBL|0145.26001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T.A. Springer, "Jordan algebras and algebraic groups" , Springer (1973) {{MR|0379618}} {{ZBL|0259.17003}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.L. Kantor, "Classification of irreducible transitively differential groups" ''Soviet Math. Dokl.'' , '''5''' (1964) pp. 1404–1407 ''Dokl. Akad. Nauk SSSR'' , '''158''' : 5 (1964) pp. 1271–1274 {{MR|175941}} {{ZBL|0286.17011}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.G. Kac, "Classification of simple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j054/j054270/j05427091.png" />-graded Lie superalgebras and simple Jordan superalgebras" ''Comm. in Algebra'' , '''5''' : 13 (1977) pp. 1375–1400 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Braun, M. Koecher, "Jordan-algebren" , Springer (1966) {{MR|0204470}} {{ZBL|0145.26001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T.A. Springer, "Jordan algebras and algebraic groups" , Springer (1973) {{MR|0379618}} {{ZBL|0259.17003}} </TD></TR></table> | ||
| + | |||
| + | [[Category:Nonassociative rings and algebras]] | ||
Latest revision as of 19:51, 15 March 2023
An algebra in which the identities $$
x y = y x ,
( x ^{2} y ) x = x ^{2} ( y x )
$$
hold. Such algebras first arose in the paper [1] of P. Jordan devoted to the axiomatic foundation of quantum mechanics (cf. also [2]), and later found application in algebra, analysis and geometry.
Let $ A $ be an associative algebra over a field of characteristic $ \neq 2 $( cf. also Associative rings and algebras). The set $ A $ together with the operations of addition and Jordan multiplication $$ a \circ b = \frac{a b + b a}{2} $$ forms the algebra $ A ^{(+)} $, which is a Jordan algebra. A Jordan algebra that is isomorphic to a subalgebra of $ A ^{(+)} $ for some associative algebra $ A $ is called special. The role of special algebras in the theory of Jordan algebras is in many respects analogous to the role of associative algebras in the theory of alternative algebras (cf. also Alternative rings and algebras). At the basis of this analogy lies the theorem that every two-generated subalgebra of a Jordan algebra is special. (Every two-generated subalgebra of an alternative algebra is associative.) However, the class of special Jordan algebras is not a variety, i.e. it is not given by identities, since special Jordan algebras can have non-special homomorphic images. Nevertheless, identities of degree 8 or 9 have been found that are satisfied by every special Jordan algebra, but are not satisfied by some non-special algebra, while it has been proved that such identities of degree $ \leq 7 $ do not exist. A necessary and sufficient condition on an algebra to be special is: A Jordan algebra is special if and only if it can be isomorphically imbedded in a Jordan algebra each countable subset of which lies in a subalgebra generated by two elements.
Examples.
1) Let $ V $ be a vector space over a field with a symmetric bilinear form $ f ( x ,\ y ) $, and let $ F \cdot e _{0} + V $ be a space of one dimension higher, on which $$ ( \alpha e _{0} + u ) ( \beta e _{0} + v ) = [ \alpha \beta + f ( u ,\ v ) ] e _{0} + \alpha v + \beta u $$ determines the multiplication ( $ \alpha ,\ \beta \in F $; $ u ,\ v \in V $). The algebra that arises is called the algebra with symmetric bilinear form $ f $. It can be isomorphically imbedded in the algebra $ C ( V ,\ f \ ) ^{(+)} $, where $ C ( V ,\ f \ ) $ is the Clifford algebra of $ f $, and is therefore a special Jordan algebra.
2) Let $ A $ be an associative algebra and $ j $ an involution of it (an anti-isomorphism of order two). The set $$ H ( A ,\ j ) = \{ {a \in A} : {a ^{j} = a} \} $$ is a subalgebra in $ A ^{(+)} $ and is also a special Jordan algebra.
3) Let $ C $ be an alternative non-associative algebra over a field $ F $ with involution $ c \mapsto \overline{c} $ whose fixed elements lie in the associative centre of $ C $. In the algebra $ C _{3} $ of matrices over $ C $ of order 3, the set $$ H ( C _{3} ,\ \Gamma ) = \{ {X \in C _{3}} : {X = \Gamma ^{-1} \overline{X} {} ^ \prime \Gamma} \} , $$ where $$ \Gamma = \mathop{\rm diag}\nolimits \{ \gamma _{1} ,\ \gamma _{2} ,\ \gamma _{3} \} , \gamma _{i} \neq 0 , \gamma _{i} \in F , $$ is a non-special Jordan algebra under the operations of addition and Jordan multiplication. This algebra is not the homomorphic image of any special algebra.
The finite-dimensional simple Jordan algebras over an algebraically closed field $ F $ of characteristic $ \neq 2 $ have been completely classified (cf. [3]). The central simple finite-dimensional Jordan algebras split into five series. The series –(D) are infinite and consist of special algebras, (E) consists of a single non-special algebra:
$ F _{n} ^{(+)} $;
(B) $ H ( F _{n} ,\ J _{1} ) $,
where $ J _{1} : \ X \rightarrow X ^ \prime $;
(C) $ H ( F _{2n} ,\ J _{S} ) $,
where $ J _{S} : \ X \rightarrow \overline{S} {} ^ \prime X ^ \prime S $,
$ S = \mathop{\rm diag}\nolimits \{ Q \dots Q \} $,
$$
Q = \left (
\begin{array}{ll}
0 & 1 \\
1 & 0 \\
\end{array}
\ \right ) ;
$$(
D) $ F \cdot e _{0} + V $
— the algebras of symmetric non-degenerate bilinear forms;
(E) $ H ( C _{3} ,\ J _{1} ) $, where $ C $ is the Cayley–Dickson algebra with the standard involution. This algebra is $ 27 $- dimensional over $ F $.
In each finite-dimensional Jordan algebra $ J $
the radical (the largest nil radical) $ N $
is involutory and the quotient algebra $ \overline{J} = J / N $
is a finite direct sum of simple Jordan algebras. If $ \overline{J} $
is separable, then $ J $
has a decomposition $ J = N + W $
into the sum of the radical and a semi-simple subalgebra $ W $
that is isomorphic to $ \overline{J} $.
In the case of characteristic 0, all semi-simple terms $ W $
are conjugate relative to automorphisms of a special kind (cf. [3]). This is also true in characteristic $ p > 0 $
if some restrictions are imposed on the algebra.
A generalization of the theory of finite-dimensional Jordan algebras is the theory of Jordan algebras with the minimum condition for quadratic (inner) ideals (cf. [3], [4], [5]). A quadratic ideal $ Q $ of an algebra $ J $ is a subspace for which $ \{ qx q \} \in Q $ for all $ q \in Q $ and $ x \in J $, where $ \{ a b c \} = ( a b) c + ( b c ) a - ( c a ) b $ is the triple Jordan product. If $ J $ is a Jordan algebra with the minimum condition for quadratic ideals and $ R $ is its quadratic radical (cf. Radical of rings and algebras), then the quotient algebra $ J / R $ is a finite direct sum of simple algebras, which have been described apart from the Jordan algebras with division. If $ J $ is a special algebra, it has been proved that the radical $ R $ is nilpotent and finite-dimensional.
An algebraic special Jordan algebra (cf. also Algebraic algebra) that satisfies a non-trivial (for special algebras) identity is locally finite-dimensional; a special Jordan nil algebra (cf. also Nil algebra) with a non-trivial identity is locally nilpotent [6]. In particular, a special algebraic Jordan (nil) algebra of bounded index is locally finite-dimensional (nilpotent). A finitely-generated solvable Jordan algebra is nilpotent; this is not true for special algebras in the general case. A Jordan $ \Phi $- operator ring that is a finitely-generated $ \Phi $- module with nilpotent generating elements, is nilpotent [7].
With each Jordan algebra one can in various ways associate a Lie algebra (cf. [3], [8]). A number of theorems on Jordan algebras have been obtained from known theorems on Lie algebras. E.g., it has been proved that a semi-simple finite-dimensional Jordan algebra over an algebraically closed field of characteristic zero has a basis with integral structure constants. For the theory of Lie algebras this construction is also useful, since certain important classes of Lie algebras can be realized by it. E.g., the Lie algebra of derivations of the simple Lie algebra of type (E) is the exceptional simple Lie algebra $ F _{4} $, the algebra of linear transformations of this algebra that leave invariant some cubic form is the exceptional simple Lie algebra $ E _{6} $. All five exceptional Lie algebras of types $ G _{2} $, $ F _{4} $, $ E _{6} $, $ E _{7} $, $ E _{8} $ can be realized by another construction, associating to an alternative algebra of degree 2 and a Jordan algebra of degree 3 some Lie algebra.
It is, finally, interesting to note that some algebras arising in genetics are Jordan algebras [10].
References
| [1] | P. Jordan, "Ueber Verallgemeinerungsmöglichkeiten des Formalismus der Quantenmechanik" Nachr. Akad. Wiss. Göttingen. Math. Phys. Kl. I , 41 (1933) pp. 209–217 Zbl 0007.08502 Zbl 59.0796.02 |
| [2] | G.G. Emch, "Algebraic methods in statistical mechanics and quantum field theory" , Wiley (1972) Zbl 0235.46085 |
| [3] | N. Jacobson, "Structure and representations of Jordan algebras" , Amer. Math. Soc. (1968) MR0251099 Zbl 0218.17010 |
| [4] | K. McCrimmon, "The radical of a Jordan algebra" Proc. Nat. Acad. Sci. USA , 62 : 3 (1969) pp. 671–678 |
| [5] | A.M. Slin'ko, "On the Jacobson radical and absolute zero divisors of special Jordan algebras" Algebra and Logic , 11 : 6 (1972) pp. 396–402 Algebra i Logika , 11 : 6 (1972) pp. 711–724 Zbl 0284.17009 |
| [6] | A.I. Shirshov, "On some non-associative null rings and algebraic algebras" Mat. Sb. , 41 : 3 (1957) pp. 381–394 (In Russian) |
| [7] | I.P. Shestakov, "Certain classes of noncommutative Jordan rings" Algebra and Logic , 10 : 4 (1971) pp. 252–280 Algebra i Logika , 10 : 4 (1971) pp. 407–448 Zbl 0259.17001 |
| [8] | R.D. Schafer, "An introduction to nonassociative algebras" , Acad. Press (1966) MR0210757 Zbl 0145.25601 |
| [9] | S.R. Gordon, "An integral basis theorem for Jordan algebras" J. of Algebra , 24 (1973) pp. 258–282 MR0308229 Zbl 0253.17010 |
| [10] | R.D. Schafer, "Structure of genetic algebras" Amer. J. Math. , 71 (1949) pp. 121–135 MR0027751 Zbl 0034.02004 |
| [11] | M. Koecher, "An elementary approach to bounded symmetric domains" , Rice Univ. (1969) MR0261032 Zbl 0217.10901 |
| [12] | A.M. Slin'ko, et al., "Jordan algebras" , 1 , Novosibirsk (1976) (In Russian) Zbl 0405.17013 Zbl 0343.17007 |
Comments
For Jordan algebras in genetics see also Genetic algebra.
There exists a functor Kan [a1], called the Kantor functor, which establishes an isomorphism between the category of Jordan algebras and the category of $ \mathbf Z $- graded Lie algebras of the form $ \mathfrak g = \mathfrak g _{-1} + \mathfrak g _{0} + \mathfrak g _{1} $ with the following properties [a2]:
a) if $ a \in \mathfrak g _{0} $ or $ \mathfrak g _{1} $ and $ [a,\ \mathfrak g _{-1} ] = 0 $, then $ a = 0 $;
b) $ \mathfrak g _{1} $
contains an element $ p $
such that $ \mathfrak g _{1} = [ \mathfrak g _{0} ,\ p] + kp $,
and $ [ \mathfrak g _{-1} ,\ p] $
generates the subalgebra $ \mathfrak g _{0} $(
$ k $
is the base field).
The construction of $ \mathop{\rm Kan}\nolimits ^{-1} $ is very simple: $ \mathop{\rm Kan}\nolimits ^{-1} ( \mathfrak g ) = \mathfrak g _{-1} $ with product $ a \cdot b = [[p,\ a],\ b] $.
This construction was extended to the super-algebra case and used to classify simple finite-dimensional Jordan super-algebras [a2].
References
| [a1] | I.L. Kantor, "Classification of irreducible transitively differential groups" Soviet Math. Dokl. , 5 (1964) pp. 1404–1407 Dokl. Akad. Nauk SSSR , 158 : 5 (1964) pp. 1271–1274 MR175941 Zbl 0286.17011 |
| [a2] | V.G. Kac, "Classification of simple 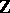 -graded Lie superalgebras and simple Jordan superalgebras" Comm. in Algebra , 5 : 13 (1977) pp. 1375–1400 -graded Lie superalgebras and simple Jordan superalgebras" Comm. in Algebra , 5 : 13 (1977) pp. 1375–1400 |
| [a3] | H. Braun, M. Koecher, "Jordan-algebren" , Springer (1966) MR0204470 Zbl 0145.26001 |
| [a4] | T.A. Springer, "Jordan algebras and algebraic groups" , Springer (1973) MR0379618 Zbl 0259.17003 |
Jordan algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan_algebra&oldid=21878