Difference between revisions of "Ornstein-Uhlenbeck process"
Ulf Rehmann (talk | contribs) m (moved Ornstein–Uhlenbeck process to Ornstein-Uhlenbeck process: ascii title) |
m (fixing superscripts) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | A | + | <!-- |
| + | o0702401.png | ||
| + | $#A+1 = 55 n = 1 | ||
| + | $#C+1 = 55 : ~/encyclopedia/old_files/data/O070/O.0700240 Ornstein\ANDUhlenbeck process | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | A Gaussian stationary random process $ V( t) $ | ||
| + | with zero expectation and an exponentially damped correlation function of the form | ||
| + | |||
| + | $$ | ||
| + | {\mathsf E} V( t) V( t + \tau ) = \ | ||
| + | B( \tau ) = \sigma ^ {2} \mathop{\rm exp} (- \alpha | \tau | ),\ \alpha > 0. | ||
| + | $$ | ||
An Ornstein–Uhlenbeck process can also be defined as a stationary solution of the stochastic equation (Langevin equation): | An Ornstein–Uhlenbeck process can also be defined as a stationary solution of the stochastic equation (Langevin equation): | ||
| − | + | $$ \tag{* } | |
| + | m dV( t) + \beta V( t) dt = dW( t), | ||
| + | $$ | ||
| − | where | + | where $ W( t) $ |
| + | is a [[Wiener process|Wiener process]] (i.e. a process for which $ dW( t)/dt = W ^ \prime ( t) $ | ||
| + | is a [[White noise|white noise]] process), while $ m $ | ||
| + | and $ \beta $ | ||
| + | are positive constants with $ \beta /m = \alpha $. | ||
| − | Equation (*) approximately describes a one-dimensional [[Brownian motion|Brownian motion]] of a free particle in a fluid; | + | Equation (*) approximately describes a one-dimensional [[Brownian motion|Brownian motion]] of a free particle in a fluid; $ V( t) $ |
| + | is here interpreted as the velocity of the particle, $ m $ | ||
| + | is its mass, $ - \beta V( t) $ | ||
| + | is the force of "viscous friction" proportional to the velocity (for a spherical particle of radius $ a $, | ||
| + | the coefficient $ \beta $ | ||
| + | is equal to $ 6 \pi \eta a $, | ||
| + | where $ \eta $ | ||
| + | is the fluid's viscosity, by virtue of Stokes' fluid hydrodynamic law), while the white noise $ W ^ \prime ( t) $ | ||
| + | is a "random force" , which is generated by chaotic shocks from the fluid molecules in thermal motion, and is the basic cause of the Brownian motion. In the original theory of Brownian motion, developed by A. Einstein and M.V. Smoluchowski in 1905–1906, the inertia of the particle was disregarded, i.e. $ m $ | ||
| + | was taken to be equal to 0; equation (*) then led to the conclusion that the coordinate of a Brownian particle | ||
| − | + | $$ | |
| + | X( t) = \int\limits _ { 0 } ^ { t } V( t ^ \prime ) dt ^ \prime | ||
| + | $$ | ||
| − | is equal to | + | is equal to $ \beta ^ {-1} W( t) $, |
| + | i.e. is a Wiener process. The Wiener process thus describes the Einstein–Smoluchowski model of Brownian motion (hence its other name — Brownian motion process); since this process is non-differentiable, a Brownian particle in the Einstein–Smoluchowski theory does not have a finite velocity. The refined Brownian motion theory, which relies on equation (*) where $ m \neq 0 $, | ||
| + | was proposed by L.S. Ornstein and G.E. Uhlenbeck ([[#References|[1]]]; see also [[#References|[2]]]); the same theory was subsequently put forward also by S.N. Bernshtein [[#References|[3]]] and A.N. Kolmogorov [[#References|[4]]]. In the Ornstein–Uhlenbeck theory, the velocity $ V( t) $ | ||
| + | of the Brownian particle is finite, but its acceleration is infinite (since the Ornstein–Uhlenbeck process is non-differentiable); for the acceleration to be finite, the theory must be further refined by taking into account the fact that a random force differs from an idealized white noise process $ W ^ \prime ( t) $. | ||
| − | Equation (*) can also be used to describe the one-dimensional Brownian motion of a harmonic oscillator, if its mass is disregarded, where now | + | Equation (*) can also be used to describe the one-dimensional Brownian motion of a harmonic oscillator, if its mass is disregarded, where now $ V( t) $ |
| + | is interpreted as the coordinate of the oscillator, $ -( m dV)/dt $ | ||
| + | is the force of viscous friction, $ - \beta V $ | ||
| + | is a regular elastic force which forces the oscillator back to its equilibrium position, while $ W ^ \prime ( t) $ | ||
| + | is a random force which can be created by molecular shocks. In this way, the Ornstein–Uhlenbeck process also provides a model of the fluctuations for a harmonic oscillator performing a Brownian motion, analogous to the Einstein–Smoluchowski model of the Brownian motion of a free particle. | ||
| − | The Ornstein–Uhlenbeck process is a diffusion-type Markov process, homogeneous with respect to time (see [[Diffusion process|Diffusion process]]); on the other hand, a process | + | The Ornstein–Uhlenbeck process is a diffusion-type Markov process, homogeneous with respect to time (see [[Diffusion process|Diffusion process]]); on the other hand, a process $ V( t) $ |
| + | which is at the same time a stationary random process, a Gaussian process and a Markov process, is necessarily an Ornstein–Uhlenbeck process. As a Markov process, the Ornstein–Uhlenbeck process can conveniently be characterized by its transition probability density $ p( t, x, y) $, | ||
| + | which is a fundamental solution of the corresponding Fokker–Planck equation (i.e. the forward [[Kolmogorov equation|Kolmogorov equation]]) of the form | ||
| − | + | $$ | |
| + | |||
| + | \frac{\partial p }{\partial t } | ||
| + | = \ | ||
| + | \alpha | ||
| + | \frac{\partial ( yp) }{\partial y } | ||
| + | + \alpha \sigma ^ {2} | ||
| + | \frac{\partial ^ {2} p }{\partial y ^ {2} } | ||
| + | , | ||
| + | $$ | ||
and which, consequently, is given by the formula | and which, consequently, is given by the formula | ||
| − | + | $$ | |
| + | p( t, x, y) = | ||
| + | \frac{1}{[ 2 \pi \sigma ^ {2} ( 1- e ^ {- 2 \alpha t } )] ^ {2} } | ||
| + | \mathop{\rm exp} | ||
| + | \left \{ - | ||
| + | \frac{( y- xe ^ {- \alpha t } ) ^ {2} }{2 \sigma ^ {2} ( 1- e ^ {- 2 | ||
| + | \alpha t } ) } | ||
| + | \right \} . | ||
| + | $$ | ||
| − | Many properties of the Ornstein–Uhlenbeck process | + | Many properties of the Ornstein–Uhlenbeck process $ V( t) $( |
| + | including its Markov property) can be deduced from known properties of a Wiener process, using the fact that the process | ||
| − | + | $$ | |
| + | W _ {0} ( t) = | ||
| + | \frac{\sqrt t } \sigma | ||
| + | V \left ( | ||
| + | \frac{ \mathop{\rm ln} t }{2 \alpha } | ||
| + | \right ) | ||
| + | $$ | ||
is a standard Wiener process (see [[#References|[5]]]). It therefore follows, in particular, that the realizations of an Ornstein–Uhlenbeck process are continuous and nowhere differentiable with probability 1, and that | is a standard Wiener process (see [[#References|[5]]]). It therefore follows, in particular, that the realizations of an Ornstein–Uhlenbeck process are continuous and nowhere differentiable with probability 1, and that | ||
| − | + | $$ | |
| + | \overline{\lim\limits}\; _ {t \rightarrow 0 } | ||
| + | \frac{| V( t) - V( 0) | }{\sqrt {4 \alpha \sigma ^ {2} t \mathop{\rm ln} \mathop{\rm ln} \ | ||
| + | {1/t } } } | ||
| + | = 1,\ \ | ||
| + | \overline{\lim\limits}\; _ {t \rightarrow \infty } | ||
| + | \frac{| V( t) | }{\sqrt {2 \sigma ^ {2} \mathop{\rm ln} t } } | ||
| + | = 1 , | ||
| + | $$ | ||
with probability 1. | with probability 1. | ||
| Line 37: | Line 111: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.E. Uhlenbeck, L.S. Ornstein, "On the theory of Brownian motion" ''Phys. Rev.'' , '''36''' (1930) pp. 823–841</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Chandrasekhar, "Stochastic problems in physics and astronomy" ''Rev. Modern Phys.'' , '''15''' (1943) pp. 1–89</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.N. Bernshtein, "Sur les chaînes linéaires de Markov quasi-continues" ''Dokl. Akad. Nauk. SSSR'' , '''1''' : 1 (1934) pp. 4–9</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Kolmogorov, "Zufällige Bewegungen (zur Theorie der Brownschen Bewegung)" ''Ann. of Math.'' , '''35''' (1934) pp. 116–117</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.L. Doob, "The Brownian movement and stochastic equations" ''Ann. of Math.'' , '''43''' (1942) pp. 351–369</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.E. Uhlenbeck, L.S. Ornstein, "On the theory of Brownian motion" ''Phys. Rev.'' , '''36''' (1930) pp. 823–841</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S. Chandrasekhar, "Stochastic problems in physics and astronomy" ''Rev. Modern Phys.'' , '''15''' (1943) pp. 1–89</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S.N. Bernshtein, "Sur les chaînes linéaires de Markov quasi-continues" ''Dokl. Akad. Nauk. SSSR'' , '''1''' : 1 (1934) pp. 4–9</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Kolmogorov, "Zufällige Bewegungen (zur Theorie der Brownschen Bewegung)" ''Ann. of Math.'' , '''35''' (1934) pp. 116–117</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.L. Doob, "The Brownian movement and stochastic equations" ''Ann. of Math.'' , '''43''' (1942) pp. 351–369</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | References [[#References|[1]]], [[#References|[2]]], [[#References|[3]]] above are reprinted in [[#References|[a1]]]. The characterization of the Ornstein–Uhlenbeck process as the only stationary Gaussian Markov process is somewhat inaccurate. A precise statement, sometimes known as Doob's theorem, is the following [[#References|[5]]]. A stationary, Gaussian Markov process | + | References [[#References|[1]]], [[#References|[2]]], [[#References|[3]]] above are reprinted in [[#References|[a1]]]. The characterization of the Ornstein–Uhlenbeck process as the only stationary Gaussian Markov process is somewhat inaccurate. A precise statement, sometimes known as Doob's theorem, is the following [[#References|[5]]]. A stationary, Gaussian Markov process $ V( t) $ |
| + | with mean $ m $ | ||
| + | and variance $ \sigma ^ {2} $ | ||
| + | is one of the following types: | ||
| − | a) if < | + | a) if $ t _ {1} < \dots < t _ {n} $, |
| + | then $ V( t _ {1} ) \dots V( t _ {n} ) $ | ||
| + | are mutually-independent Gaussian random variables, with mean $ m $ | ||
| + | and variance $ \sigma ^ {2} $; | ||
| − | b) there exists a constant | + | b) there exists a constant $ \alpha > 0 $ |
| + | such that if $ t _ {1} < \dots < t _ {n} $, | ||
| + | then $ V( t _ {1} ) \dots V( t _ {n} ) $ | ||
| + | have an $ n $- | ||
| + | variate Gaussian distribution, with common mean $ m $ | ||
| + | and variance $ \sigma ^ {2} $, | ||
| + | and correlation function $ {\mathsf E} \{ [ V( t+ \tau )- m ] [ V( t)- m ] \} = \sigma ^ {2} \mathop{\rm exp} (- \alpha | \tau | ) $. | ||
| − | For a generalization to the | + | For a generalization to the $ n $- |
| + | dimensional case see the paper by M.C. Wang and G.E. Uhlenbeck, reprinted in [[#References|[a1]]]. For a characterization of a Gaussian Markov process which is not necessarily stationary, see [[#References|[a2]]]. The relation to the Wiener process is also discussed in [[#References|[a3]]]. | ||
| − | Let | + | Let $ \mu $ |
| + | be any Gaussian measure on a (possibly infinite-dimensional) locally convex space $ E $. | ||
| + | Then one can define a Markov semi-group on $ E $ | ||
| + | using Mehler's formula | ||
| − | + | $$ | |
| + | P _ {t} ( x , f ) = \int\limits _ { E } | ||
| + | f ( e ^ {-t/2} x + \sqrt {1- e ^ {-t} } y ) \mu ( dy) \ ( x \in E) , | ||
| + | $$ | ||
| − | + | $ f $ | |
| + | denoting a continuous bounded function on $ E $. | ||
| + | This semi-group admits the measure $ \mu $ | ||
| + | as a symmetric invariant measure, and in the finite-dimensional case it reduces to an Ornstein–Uhlenbeck semi-group of the kind described in the main article above. Since there is no Lebesgue measure in infinite-dimensional situations (it is often replaced by a Gaussian measure), the Ornstein–Uhlenbeck semi-group, and its generator as an infinite-dimensional "Laplacian" , have recently played a considerable role in infinite-dimensional analysis. See [[#References|[a4]]], [[#References|[a5]]]. For other extensions of the Ornstein–Uhlenbeck process to infinite-dimensional situations, see [[#References|[a6]]], [[#References|[a8]]]–[[#References|[a10]]]. For historical and physical background see [[#References|[a7]]]. See also [[Langevin equation|Langevin equation]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Wax (ed.) , ''Selected papers on noise and stochastic processes'' , Dover, reprint (1954)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Iranpour, P. Chacon, "Basic stochastic processes" , ''The Marc Kac lectures'' , Macmillan (1988)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.R. Cox, H.D. Miller, "The theory of stochastic processes" , Methuen (1965)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Malliavin, "Stochastic calculus of variations and hypoelliptic operators" K. Itô (ed.) , ''Proc. Internat. Conf. Stochastic Differential Equations (Kyoto, 1976)'' , Wiley (1978) pp. 195–263</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D.W. Stroock, "The Malliavin calculus, a functional analytic approach" ''J. Funct. Anal.'' , '''44''' (1981) pp. 212–257</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> B. Schmuland, "Regularity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070240/o07024056.png" />-valued Ornstein–Uhlenbeck processes" ''C.R. Math. Acad. Sci. Soc. R. Canada'' , '''10''' (1988) pp. 119–124</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E. Nelson, "Dynamical theories of Brownian motion" , Princeton Univ. Press (1967)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> M. Röckner, "Traces of harmonic functions and a new path space for the free quantum field" ''J. Funct. Anal.'' , '''79''' (1988) pp. 211–249</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> T. Kolsrud, "Gaussian random fields, infinite dimensional Ornstein–Uhlenbeck processes, and symmetric Markov processes" ''Acta Appl. Math.'' , '''12''' (1988) pp. 237–263</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> P.A. Meyer, "Transformations de Riesz pour les lois Gaussiennes" J. Azéma (ed.) M. Yor (ed.) , ''Sem. Probab. XVIII'' , ''Lect. notes in math.'' , '''1059''' , Springer (1984) pp. 179–193</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> L.C.G. Rogers, D. Williams, "Diffusion, Markov processes and martingales" , '''I-II''' , Wiley (1987)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1988)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Wax (ed.) , ''Selected papers on noise and stochastic processes'' , Dover, reprint (1954)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Iranpour, P. Chacon, "Basic stochastic processes" , ''The Marc Kac lectures'' , Macmillan (1988)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.R. Cox, H.D. Miller, "The theory of stochastic processes" , Methuen (1965)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P. Malliavin, "Stochastic calculus of variations and hypoelliptic operators" K. Itô (ed.) , ''Proc. Internat. Conf. Stochastic Differential Equations (Kyoto, 1976)'' , Wiley (1978) pp. 195–263</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D.W. Stroock, "The Malliavin calculus, a functional analytic approach" ''J. Funct. Anal.'' , '''44''' (1981) pp. 212–257</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> B. Schmuland, "Regularity of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070240/o07024056.png" />-valued Ornstein–Uhlenbeck processes" ''C.R. Math. Acad. Sci. Soc. R. Canada'' , '''10''' (1988) pp. 119–124</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E. Nelson, "Dynamical theories of Brownian motion" , Princeton Univ. Press (1967)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> M. Röckner, "Traces of harmonic functions and a new path space for the free quantum field" ''J. Funct. Anal.'' , '''79''' (1988) pp. 211–249</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> T. Kolsrud, "Gaussian random fields, infinite dimensional Ornstein–Uhlenbeck processes, and symmetric Markov processes" ''Acta Appl. Math.'' , '''12''' (1988) pp. 237–263</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> P.A. Meyer, "Transformations de Riesz pour les lois Gaussiennes" J. Azéma (ed.) M. Yor (ed.) , ''Sem. Probab. XVIII'' , ''Lect. notes in math.'' , '''1059''' , Springer (1984) pp. 179–193</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> L.C.G. Rogers, D. Williams, "Diffusion, Markov processes and martingales" , '''I-II''' , Wiley (1987)</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1988)</TD></TR></table> | ||
Latest revision as of 12:14, 21 March 2022
A Gaussian stationary random process $ V( t) $
with zero expectation and an exponentially damped correlation function of the form
$$ {\mathsf E} V( t) V( t + \tau ) = \ B( \tau ) = \sigma ^ {2} \mathop{\rm exp} (- \alpha | \tau | ),\ \alpha > 0. $$
An Ornstein–Uhlenbeck process can also be defined as a stationary solution of the stochastic equation (Langevin equation):
$$ \tag{* } m dV( t) + \beta V( t) dt = dW( t), $$
where $ W( t) $ is a Wiener process (i.e. a process for which $ dW( t)/dt = W ^ \prime ( t) $ is a white noise process), while $ m $ and $ \beta $ are positive constants with $ \beta /m = \alpha $.
Equation (*) approximately describes a one-dimensional Brownian motion of a free particle in a fluid; $ V( t) $ is here interpreted as the velocity of the particle, $ m $ is its mass, $ - \beta V( t) $ is the force of "viscous friction" proportional to the velocity (for a spherical particle of radius $ a $, the coefficient $ \beta $ is equal to $ 6 \pi \eta a $, where $ \eta $ is the fluid's viscosity, by virtue of Stokes' fluid hydrodynamic law), while the white noise $ W ^ \prime ( t) $ is a "random force" , which is generated by chaotic shocks from the fluid molecules in thermal motion, and is the basic cause of the Brownian motion. In the original theory of Brownian motion, developed by A. Einstein and M.V. Smoluchowski in 1905–1906, the inertia of the particle was disregarded, i.e. $ m $ was taken to be equal to 0; equation (*) then led to the conclusion that the coordinate of a Brownian particle
$$ X( t) = \int\limits _ { 0 } ^ { t } V( t ^ \prime ) dt ^ \prime $$
is equal to $ \beta ^ {-1} W( t) $, i.e. is a Wiener process. The Wiener process thus describes the Einstein–Smoluchowski model of Brownian motion (hence its other name — Brownian motion process); since this process is non-differentiable, a Brownian particle in the Einstein–Smoluchowski theory does not have a finite velocity. The refined Brownian motion theory, which relies on equation (*) where $ m \neq 0 $, was proposed by L.S. Ornstein and G.E. Uhlenbeck ([1]; see also [2]); the same theory was subsequently put forward also by S.N. Bernshtein [3] and A.N. Kolmogorov [4]. In the Ornstein–Uhlenbeck theory, the velocity $ V( t) $ of the Brownian particle is finite, but its acceleration is infinite (since the Ornstein–Uhlenbeck process is non-differentiable); for the acceleration to be finite, the theory must be further refined by taking into account the fact that a random force differs from an idealized white noise process $ W ^ \prime ( t) $.
Equation (*) can also be used to describe the one-dimensional Brownian motion of a harmonic oscillator, if its mass is disregarded, where now $ V( t) $ is interpreted as the coordinate of the oscillator, $ -( m dV)/dt $ is the force of viscous friction, $ - \beta V $ is a regular elastic force which forces the oscillator back to its equilibrium position, while $ W ^ \prime ( t) $ is a random force which can be created by molecular shocks. In this way, the Ornstein–Uhlenbeck process also provides a model of the fluctuations for a harmonic oscillator performing a Brownian motion, analogous to the Einstein–Smoluchowski model of the Brownian motion of a free particle.
The Ornstein–Uhlenbeck process is a diffusion-type Markov process, homogeneous with respect to time (see Diffusion process); on the other hand, a process $ V( t) $ which is at the same time a stationary random process, a Gaussian process and a Markov process, is necessarily an Ornstein–Uhlenbeck process. As a Markov process, the Ornstein–Uhlenbeck process can conveniently be characterized by its transition probability density $ p( t, x, y) $, which is a fundamental solution of the corresponding Fokker–Planck equation (i.e. the forward Kolmogorov equation) of the form
$$ \frac{\partial p }{\partial t } = \ \alpha \frac{\partial ( yp) }{\partial y } + \alpha \sigma ^ {2} \frac{\partial ^ {2} p }{\partial y ^ {2} } , $$
and which, consequently, is given by the formula
$$ p( t, x, y) = \frac{1}{[ 2 \pi \sigma ^ {2} ( 1- e ^ {- 2 \alpha t } )] ^ {2} } \mathop{\rm exp} \left \{ - \frac{( y- xe ^ {- \alpha t } ) ^ {2} }{2 \sigma ^ {2} ( 1- e ^ {- 2 \alpha t } ) } \right \} . $$
Many properties of the Ornstein–Uhlenbeck process $ V( t) $( including its Markov property) can be deduced from known properties of a Wiener process, using the fact that the process
$$ W _ {0} ( t) = \frac{\sqrt t } \sigma V \left ( \frac{ \mathop{\rm ln} t }{2 \alpha } \right ) $$
is a standard Wiener process (see [5]). It therefore follows, in particular, that the realizations of an Ornstein–Uhlenbeck process are continuous and nowhere differentiable with probability 1, and that
$$ \overline{\lim\limits}\; _ {t \rightarrow 0 } \frac{| V( t) - V( 0) | }{\sqrt {4 \alpha \sigma ^ {2} t \mathop{\rm ln} \mathop{\rm ln} \ {1/t } } } = 1,\ \ \overline{\lim\limits}\; _ {t \rightarrow \infty } \frac{| V( t) | }{\sqrt {2 \sigma ^ {2} \mathop{\rm ln} t } } = 1 , $$
with probability 1.
References
| [1] | G.E. Uhlenbeck, L.S. Ornstein, "On the theory of Brownian motion" Phys. Rev. , 36 (1930) pp. 823–841 |
| [2] | S. Chandrasekhar, "Stochastic problems in physics and astronomy" Rev. Modern Phys. , 15 (1943) pp. 1–89 |
| [3] | S.N. Bernshtein, "Sur les chaînes linéaires de Markov quasi-continues" Dokl. Akad. Nauk. SSSR , 1 : 1 (1934) pp. 4–9 |
| [4] | A.N. Kolmogorov, "Zufällige Bewegungen (zur Theorie der Brownschen Bewegung)" Ann. of Math. , 35 (1934) pp. 116–117 |
| [5] | J.L. Doob, "The Brownian movement and stochastic equations" Ann. of Math. , 43 (1942) pp. 351–369 |
Comments
References [1], [2], [3] above are reprinted in [a1]. The characterization of the Ornstein–Uhlenbeck process as the only stationary Gaussian Markov process is somewhat inaccurate. A precise statement, sometimes known as Doob's theorem, is the following [5]. A stationary, Gaussian Markov process $ V( t) $ with mean $ m $ and variance $ \sigma ^ {2} $ is one of the following types:
a) if $ t _ {1} < \dots < t _ {n} $, then $ V( t _ {1} ) \dots V( t _ {n} ) $ are mutually-independent Gaussian random variables, with mean $ m $ and variance $ \sigma ^ {2} $;
b) there exists a constant $ \alpha > 0 $ such that if $ t _ {1} < \dots < t _ {n} $, then $ V( t _ {1} ) \dots V( t _ {n} ) $ have an $ n $- variate Gaussian distribution, with common mean $ m $ and variance $ \sigma ^ {2} $, and correlation function $ {\mathsf E} \{ [ V( t+ \tau )- m ] [ V( t)- m ] \} = \sigma ^ {2} \mathop{\rm exp} (- \alpha | \tau | ) $.
For a generalization to the $ n $- dimensional case see the paper by M.C. Wang and G.E. Uhlenbeck, reprinted in [a1]. For a characterization of a Gaussian Markov process which is not necessarily stationary, see [a2]. The relation to the Wiener process is also discussed in [a3].
Let $ \mu $ be any Gaussian measure on a (possibly infinite-dimensional) locally convex space $ E $. Then one can define a Markov semi-group on $ E $ using Mehler's formula
$$ P _ {t} ( x , f ) = \int\limits _ { E } f ( e ^ {-t/2} x + \sqrt {1- e ^ {-t} } y ) \mu ( dy) \ ( x \in E) , $$
$ f $ denoting a continuous bounded function on $ E $. This semi-group admits the measure $ \mu $ as a symmetric invariant measure, and in the finite-dimensional case it reduces to an Ornstein–Uhlenbeck semi-group of the kind described in the main article above. Since there is no Lebesgue measure in infinite-dimensional situations (it is often replaced by a Gaussian measure), the Ornstein–Uhlenbeck semi-group, and its generator as an infinite-dimensional "Laplacian" , have recently played a considerable role in infinite-dimensional analysis. See [a4], [a5]. For other extensions of the Ornstein–Uhlenbeck process to infinite-dimensional situations, see [a6], [a8]–[a10]. For historical and physical background see [a7]. See also Langevin equation.
References
| [a1] | N. Wax (ed.) , Selected papers on noise and stochastic processes , Dover, reprint (1954) |
| [a2] | R. Iranpour, P. Chacon, "Basic stochastic processes" , The Marc Kac lectures , Macmillan (1988) |
| [a3] | D.R. Cox, H.D. Miller, "The theory of stochastic processes" , Methuen (1965) |
| [a4] | P. Malliavin, "Stochastic calculus of variations and hypoelliptic operators" K. Itô (ed.) , Proc. Internat. Conf. Stochastic Differential Equations (Kyoto, 1976) , Wiley (1978) pp. 195–263 |
| [a5] | D.W. Stroock, "The Malliavin calculus, a functional analytic approach" J. Funct. Anal. , 44 (1981) pp. 212–257 |
| [a6] | B. Schmuland, "Regularity of 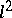 -valued Ornstein–Uhlenbeck processes" C.R. Math. Acad. Sci. Soc. R. Canada , 10 (1988) pp. 119–124 -valued Ornstein–Uhlenbeck processes" C.R. Math. Acad. Sci. Soc. R. Canada , 10 (1988) pp. 119–124 |
| [a7] | E. Nelson, "Dynamical theories of Brownian motion" , Princeton Univ. Press (1967) |
| [a8] | M. Röckner, "Traces of harmonic functions and a new path space for the free quantum field" J. Funct. Anal. , 79 (1988) pp. 211–249 |
| [a9] | T. Kolsrud, "Gaussian random fields, infinite dimensional Ornstein–Uhlenbeck processes, and symmetric Markov processes" Acta Appl. Math. , 12 (1988) pp. 237–263 |
| [a10] | P.A. Meyer, "Transformations de Riesz pour les lois Gaussiennes" J. Azéma (ed.) M. Yor (ed.) , Sem. Probab. XVIII , Lect. notes in math. , 1059 , Springer (1984) pp. 179–193 |
| [a11] | L.C.G. Rogers, D. Williams, "Diffusion, Markov processes and martingales" , I-II , Wiley (1987) |
| [a12] | I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1988) |
Ornstein-Uhlenbeck process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ornstein-Uhlenbeck_process&oldid=22865