Difference between revisions of "Gram-Charlier series"
(Importing text file) |
m (fixing superscripts) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | g0447301.png | ||
| + | $#A+1 = 34 n = 1 | ||
| + | $#C+1 = 34 : ~/encyclopedia/old_files/data/G044/G.0404730 Gram\ANDCharlier series | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | {{MSC|60E99}} | ||
| + | |||
| + | [[Category:Distribution theory]] | ||
| + | |||
A series defined by the expression | A series defined by the expression | ||
| − | + | $$ \tag{1 } | |
| + | f _ {A} ( x) = \ | ||
| + | f ( x) + | ||
| + | \sum _ {k = 3 } ^ { n } | ||
| + | a _ {k} f ^ { ( k) } ( x) | ||
| + | $$ | ||
or | or | ||
| − | + | $$ \tag{2 } | |
| + | f _ {B} ( x) = \ | ||
| + | \psi ( x) | ||
| + | \sum _ {m = 0 } ^ { n } | ||
| + | b _ {m} g _ {m} ( x), | ||
| + | $$ | ||
| − | where | + | where $ x $ |
| + | is the normalized value of a random variable. | ||
| − | The series (1) is known as the Gram–Charlier series of type | + | The series (1) is known as the Gram–Charlier series of type $ A $; |
| + | here | ||
| − | + | $$ | |
| + | f ( x) = \ | ||
| + | { | ||
| + | \frac{1}{\sqrt {2 \pi }} | ||
| + | } | ||
| + | e ^ {- x ^ {2} /2 } , | ||
| + | $$ | ||
| − | + | $ f ^ { ( k) } $ | |
| + | is the $ k $-th derivative of $ f $, | ||
| + | which can be represented as | ||
| − | + | $$ | |
| + | f ^ { ( k) } ( x) = \ | ||
| + | (- 1) ^ {k} H _ {k} ( x) f ( x), | ||
| + | $$ | ||
| − | where | + | where $ H _ {k} ( x) $ |
| + | are the Chebyshev–Hermite polynomials. The derivatives $ f ^ { ( k) } $ | ||
| + | and the polynomials $ H _ {k} $ | ||
| + | are orthogonal, owing to which the coefficients $ a _ {k} $ | ||
| + | can be defined by the basic moments $ r _ {k} $ | ||
| + | of the given distribution series. If one restricts to the first few terms of the series (1), one obtains | ||
| − | + | $$ | |
| + | f _ {A} ( x) = \ | ||
| + | f ( x) + | ||
| + | \frac{r _ {3} }{3!} | ||
| − | + | f ^ { ( 3) } ( x) + | |
| + | $$ | ||
| − | + | $$ | |
| + | + | ||
| − | + | \frac{r _ {4} - 3 }{4! } | |
| + | f ^ { ( 4) } ( x) - | ||
| + | \frac{r _ {5} - 10r _ {3} }{5! } | ||
| + | f ^ { ( 3) } ( x) + | ||
| + | \frac{r _ {4} - 15r _ {4} + 30 }{6! } | ||
| + | f ^ { ( 6) } ( x). | ||
| + | $$ | ||
| − | + | The series (2) is known as a Gram–Charlier series of type $ B $; | |
| + | here | ||
| + | |||
| + | $$ | ||
| + | \psi ( x) = \ | ||
| + | |||
| + | \frac{\lambda ^ {x} }{x!} | ||
| + | |||
| + | e ^ {- \lambda } ,\ \ | ||
| + | x = 0, 1 \dots | ||
| + | $$ | ||
| + | |||
| + | while $ g _ {m} ( x) $ | ||
| + | are polynomials analogous to the polynomials $ H _ {k} ( x) $. | ||
If one restricts to the first terms of the series (2), one obtains | If one restricts to the first terms of the series (2), one obtains | ||
| − | + | $$ | |
| + | f _ {B} ( x) = \ | ||
| + | |||
| + | \frac{\lambda ^ {x} }{x! } | ||
| + | |||
| + | e ^ {- \lambda } \left \{ | ||
| + | 1 + | ||
| + | \frac{\mu _ {2} - \lambda }{\lambda ^ {2} } | ||
| + | |||
| + | \left [ | ||
| + | \frac{x ^ {[2]} }{2 } | ||
| + | - | ||
| + | \lambda x ^ {[1]} + | ||
| − | + | \frac{\lambda ^ {2} }{2 } | |
| + | \right ] \right . + | ||
| + | $$ | ||
| − | + | $$ | |
| + | + \left . | ||
| − | + | \frac{\mu _ {3} - 3 \mu _ {2} + 2 \lambda }{\lambda ^ {3} } | |
| + | \left [ | ||
| + | \frac{x ^ {[3]} }{6 } | ||
| + | - | ||
| + | { | ||
| + | \frac \lambda {2} | ||
| + | } x ^ {[2]} + | ||
| + | \frac{\lambda ^ {2} }{2 } | ||
| + | x ^ {[1]} - | ||
| + | \frac{\lambda ^ {3} }{6 } | ||
| + | \right ] \right \} . | ||
| + | $$ | ||
| − | + | Here $ \mu _ {i} $ | |
| + | are the central moments of the distribution, while $ x ^ {[i]} = x( x - 1) \dots ( x - i + 1) $. | ||
| − | + | Gram–Charlier series were obtained by J.P. Gram {{Cite|G}} and C.V.L. Charlier {{Cite|Ch}} in their study of functions of the form | |
| − | + | $$ | |
| + | B _ {0} ( x) = \ | ||
| + | { | ||
| + | \frac{1}{2 \pi } | ||
| + | } | ||
| + | \int\limits _ {- \pi } ^ { {+ } \pi } | ||
| + | e ^ {- itx } \phi ( t) dt. | ||
| + | $$ | ||
| − | + | These are convenient for the interpolation between the values $ B ( m) = ( n!/m! ( n - m)!) p ^ {m} q ^ {n-m} $ | |
| + | of the general term of the [[Binomial distribution|binomial distribution]], where | ||
| − | + | $$ | |
| − | + | \phi ( t) = \ | |
| + | ( pe ^ {it} + q) ^ {n} = \ | ||
| + | \sum _ {m = 0 } ^ { n } | ||
| + | B ( m) e ^ {itm} | ||
| + | $$ | ||
| + | is the characteristic function of the binomial distribution. The expansion of $ \mathop{\rm ln} \phi ( t) $ | ||
| + | in powers of $ t $ | ||
| + | yields a Gram–Charlier series of type $ A $ | ||
| + | for $ B _ {0} ( x) $, | ||
| + | whereas the expansion of $ \mathop{\rm ln} \phi ( t) $ | ||
| + | in powers of $ p $ | ||
| + | yields a Gram–Charlier series of type $ B $. | ||
| + | ====References==== | ||
| + | {| | ||
| + | |valign="top"|{{Ref|G}}|| J.P. Gram, "Ueber die Entwicklung reeller Funktionen in Reihen mittelst der Methode der kleinsten Quadraten" ''J. Reine Angew. Math.'' , '''94''' (1883) pp. 41–73 | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Ch}}|| C.V.L. Charlier, "Frequency curves of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044730/g04473037.png" /> in heterograde statistics" ''Ark. Mat. Astr. Fysik'' , '''9''' : 25 (1914) pp. 1–17 | ||
| + | |- | ||
| + | |valign="top"|{{Ref|M}}|| A.K. Mitropol'skii, "Curves of distributions" , Leningrad (1960) (In Russian) | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| Line 56: | Line 178: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|Cr}}|| H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. Sect. 17.6 | ||
| + | |} | ||
Latest revision as of 11:31, 21 March 2022
2020 Mathematics Subject Classification: Primary: 60E99 [MSN][ZBL]
A series defined by the expression
$$ \tag{1 } f _ {A} ( x) = \ f ( x) + \sum _ {k = 3 } ^ { n } a _ {k} f ^ { ( k) } ( x) $$
or
$$ \tag{2 } f _ {B} ( x) = \ \psi ( x) \sum _ {m = 0 } ^ { n } b _ {m} g _ {m} ( x), $$
where $ x $ is the normalized value of a random variable.
The series (1) is known as the Gram–Charlier series of type $ A $; here
$$ f ( x) = \ { \frac{1}{\sqrt {2 \pi }} } e ^ {- x ^ {2} /2 } , $$
$ f ^ { ( k) } $ is the $ k $-th derivative of $ f $, which can be represented as
$$ f ^ { ( k) } ( x) = \ (- 1) ^ {k} H _ {k} ( x) f ( x), $$
where $ H _ {k} ( x) $ are the Chebyshev–Hermite polynomials. The derivatives $ f ^ { ( k) } $ and the polynomials $ H _ {k} $ are orthogonal, owing to which the coefficients $ a _ {k} $ can be defined by the basic moments $ r _ {k} $ of the given distribution series. If one restricts to the first few terms of the series (1), one obtains
$$ f _ {A} ( x) = \ f ( x) + \frac{r _ {3} }{3!} f ^ { ( 3) } ( x) + $$
$$ + \frac{r _ {4} - 3 }{4! } f ^ { ( 4) } ( x) - \frac{r _ {5} - 10r _ {3} }{5! } f ^ { ( 3) } ( x) + \frac{r _ {4} - 15r _ {4} + 30 }{6! } f ^ { ( 6) } ( x). $$
The series (2) is known as a Gram–Charlier series of type $ B $; here
$$ \psi ( x) = \ \frac{\lambda ^ {x} }{x!} e ^ {- \lambda } ,\ \ x = 0, 1 \dots $$
while $ g _ {m} ( x) $ are polynomials analogous to the polynomials $ H _ {k} ( x) $.
If one restricts to the first terms of the series (2), one obtains
$$ f _ {B} ( x) = \ \frac{\lambda ^ {x} }{x! } e ^ {- \lambda } \left \{ 1 + \frac{\mu _ {2} - \lambda }{\lambda ^ {2} } \left [ \frac{x ^ {[2]} }{2 } - \lambda x ^ {[1]} + \frac{\lambda ^ {2} }{2 } \right ] \right . + $$
$$ + \left . \frac{\mu _ {3} - 3 \mu _ {2} + 2 \lambda }{\lambda ^ {3} } \left [ \frac{x ^ {[3]} }{6 } - { \frac \lambda {2} } x ^ {[2]} + \frac{\lambda ^ {2} }{2 } x ^ {[1]} - \frac{\lambda ^ {3} }{6 } \right ] \right \} . $$
Here $ \mu _ {i} $ are the central moments of the distribution, while $ x ^ {[i]} = x( x - 1) \dots ( x - i + 1) $.
Gram–Charlier series were obtained by J.P. Gram [G] and C.V.L. Charlier [Ch] in their study of functions of the form
$$ B _ {0} ( x) = \ { \frac{1}{2 \pi } } \int\limits _ {- \pi } ^ { {+ } \pi } e ^ {- itx } \phi ( t) dt. $$
These are convenient for the interpolation between the values $ B ( m) = ( n!/m! ( n - m)!) p ^ {m} q ^ {n-m} $ of the general term of the binomial distribution, where
$$ \phi ( t) = \ ( pe ^ {it} + q) ^ {n} = \ \sum _ {m = 0 } ^ { n } B ( m) e ^ {itm} $$
is the characteristic function of the binomial distribution. The expansion of $ \mathop{\rm ln} \phi ( t) $ in powers of $ t $ yields a Gram–Charlier series of type $ A $ for $ B _ {0} ( x) $, whereas the expansion of $ \mathop{\rm ln} \phi ( t) $ in powers of $ p $ yields a Gram–Charlier series of type $ B $.
References
| [G] | J.P. Gram, "Ueber die Entwicklung reeller Funktionen in Reihen mittelst der Methode der kleinsten Quadraten" J. Reine Angew. Math. , 94 (1883) pp. 41–73 |
| [Ch] | C.V.L. Charlier, "Frequency curves of type 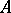 in heterograde statistics" Ark. Mat. Astr. Fysik , 9 : 25 (1914) pp. 1–17 in heterograde statistics" Ark. Mat. Astr. Fysik , 9 : 25 (1914) pp. 1–17
|
| [M] | A.K. Mitropol'skii, "Curves of distributions" , Leningrad (1960) (In Russian) |
Comments
Cf. also Edgeworth series.
References
| [Cr] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) pp. Sect. 17.6 |
Gram-Charlier series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gram-Charlier_series&oldid=18126