Difference between revisions of "Gauss-Manin connection"
Ulf Rehmann (talk | contribs) m (moved Gauss–Manin connection to Gauss-Manin connection: ascii title) |
m (fix tex) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | g0434701.png | ||
| + | $#A+1 = 52 n = 1 | ||
| + | $#C+1 = 52 : ~/encyclopedia/old_files/data/G043/G.0403470 Gauss\ANDManin connection | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The Gauss–Manin connection is a way to differentiate cohomology classes with respect to parameters. Consider a smooth projective curve $ X $ | |
| + | over a field $ K $. | ||
| + | Its first [[De Rham cohomology|de Rham cohomology]] group $ H _ { \mathop{\rm dR} } ^ {1} ( X/K) $ | ||
| + | can be identified with the space of differentials of second kind on $ X $ | ||
| + | modulo exact differentials (cf. [[Differential|Differential]]). Each derivation $ \theta $ | ||
| + | of $ K $( | ||
| + | cf. [[Derivation in a ring|Derivation in a ring]]) can be lifted in a canonical way to a mapping $ \nabla _ \theta : H _ { \mathop{\rm dR} } ^ {1} ( X/K) \rightarrow H _ { \mathop{\rm dR} } ^ {1} ( X/K) $ | ||
| + | satisfying $ \nabla _ \theta ( g \omega ) = g \nabla _ \theta ( \omega ) + \theta ( g) \omega $ | ||
| + | for $ g \in K $, | ||
| + | $ \omega \in H _ { \mathop{\rm dR} } ^ {1} ( X/K) $[[#References|[a1]]], [[#References|[a2]]]. This amounts to a [[Connection|connection]] | ||
| − | + | $$ | |
| + | \nabla : \ | ||
| + | H _ { \mathop{\rm dR} } ^ {1} ( X/K) \rightarrow \ | ||
| + | \Omega _ {K} ^ {1} \otimes H _ { \mathop{\rm dR} } ^ {1} ( X/K) | ||
| + | $$ | ||
| − | + | which is integrable (i.e. $ \nabla _ {[ \theta , \theta ^ \prime ] } = [ \nabla _ \theta , \nabla _ {\theta ^ \prime } ] $). | |
| + | If $ K $ | ||
| + | is a function field in one variable, one obtains the Picard–Fuchs equation $ \nabla \omega = 0 $, | ||
| + | which has regular singular points (cf. [[Regular singular point|Regular singular point]]). | ||
| − | and the | + | The generalization to higher dimension is due to A. Grothendieck [[#References|[a3]]]. For a proper and smooth morphism $ f: X \rightarrow S $ |
| + | of $ \mathbf C $- | ||
| + | schemes the de Rham cohomology of the fibres of $ f $ | ||
| + | is described by the locally free $ {\mathcal O} _ {S} $- | ||
| + | modules $ H _ { \mathop{\rm dR} } ^ {n} ( X/S) = R ^ {n} f _ \star ( \Omega _ {X/S} ^ {\bullet } ) $, | ||
| + | the relative de Rham cohomology sheaves. From now on suppose that $ S $ | ||
| + | is of finite type over $ \mathbf C $ | ||
| + | and let $ X ^ {h} $ | ||
| + | and $ S ^ {h} $ | ||
| + | denote the underlying analytic spaces. Then | ||
| − | + | $$ | |
| + | H _ { \mathop{\rm dR} } ^ {n} | ||
| + | ( {X ^ {h} } / {S ^ {h} } ) \cong \ | ||
| + | {\mathcal O} _ {S ^ {h} } \otimes _ {\mathbf C} R ^ {n} f _ \star \mathbf C _ {X ^ {h} } , | ||
| + | $$ | ||
| − | + | and the analytic version of the Gauss–Manin connection is defined by $ \nabla ( g \omega ) = dg \otimes \omega $ | |
| + | for $ g $( | ||
| + | respectively, $ \omega $) | ||
| + | a local section of $ {\mathcal O} _ {S ^ {h} } $( | ||
| + | respectively, $ R ^ {n} f _ \star \mathbf C _ {X ^ {h} } $). | ||
| − | + | An algebraic construction has been given by N.M. Katz and T. Oda [[#References|[a4]]]. The complex $ \Omega _ {X/ \mathbf C } ^ {\bullet } $ | |
| + | is filtered by subcomplexes $ \phi ^ {i} $, | ||
| + | where | ||
| − | + | $$ | |
| + | \phi ^ {i} \Omega _ {X/ \mathbf C } ^ {p} = \ | ||
| + | \textrm{ image } \textrm{ of } \ | ||
| + | ( f ^ { \star } \Omega _ {S/ \mathbf C } ^ {i} \otimes | ||
| + | \Omega _ {X/ \mathbf C } ^ {p - i } \rightarrow \ | ||
| + | \Omega _ {X/ \mathbf C } ^ {p} ). | ||
| + | $$ | ||
| + | |||
| + | One has $ ( \phi ^ {i} / \phi ^ {i + 1 } ) ^ {n} \cong f ^ { \star } \Omega _ {S/ \mathbf C } ^ {i} \otimes \Omega _ {X/S} ^ {n - i } $ | ||
| + | and $ R ^ {n} f _ \star ( \phi ^ {i} / \phi ^ {i + 1 } ) \cong \Omega _ {S/ \mathbf C } ^ {i} \otimes H _ { \mathop{\rm dR} } ^ {n - i } ( X/S) $. | ||
| + | The connecting homomorphism $ \nabla : R ^ {n} f _ \star ( \phi ^ {0} / \phi ^ {1} ) \rightarrow R ^ {n + 1 } f _ \star ( \phi ^ {1} / \phi ^ {2} ) $ | ||
| + | in the long exact hypercohomology sequence associated to the exact sequence | ||
| + | |||
| + | $$ | ||
| + | 0 \rightarrow \ | ||
| + | \phi ^ {1} / \phi ^ {2} \rightarrow \ | ||
| + | \phi ^ {0} / \phi ^ {2} \rightarrow \ | ||
| + | \phi ^ {0} / \phi ^ {1} \rightarrow 0 | ||
| + | $$ | ||
is an algebraic version of the Gauss–Manin connection. | is an algebraic version of the Gauss–Manin connection. | ||
| Line 23: | Line 84: | ||
The Gauss–Manin connection is regular singular [[#References|[a5]]]–[[#References|[a8]]]. Its monodromy transformations around points at infinity are quasi-unipotent [[#References|[a6]]], [[#References|[a9]]], [[#References|[a10]]], and bounds on the size of its Jordan blocks are known [[#References|[a7]]], [[#References|[a11]]]. Geometrical proofs of the monodromy theorem are due to A. Landman [[#References|[a12]]], C.H. Clemens [[#References|[a13]]] and D.T. Lê [[#References|[a14]]]. | The Gauss–Manin connection is regular singular [[#References|[a5]]]–[[#References|[a8]]]. Its monodromy transformations around points at infinity are quasi-unipotent [[#References|[a6]]], [[#References|[a9]]], [[#References|[a10]]], and bounds on the size of its Jordan blocks are known [[#References|[a7]]], [[#References|[a11]]]. Geometrical proofs of the monodromy theorem are due to A. Landman [[#References|[a12]]], C.H. Clemens [[#References|[a13]]] and D.T. Lê [[#References|[a14]]]. | ||
| − | Another important feature of the Gauss–Manin connection is Griffiths' transversality. The relative de Rham cohomology sheaves of a smooth proper morphism | + | Another important feature of the Gauss–Manin connection is Griffiths' transversality. The relative de Rham cohomology sheaves of a smooth proper morphism $ f: X \rightarrow S $ |
| + | can be filtered as follows. Let $ F ^ { p } \Omega _ {X/S} ^ {\bullet } $ | ||
| + | be the subcomplex | ||
| − | + | $$ | |
| + | [ 0 \rightarrow \dots \rightarrow 0 \rightarrow \ | ||
| + | \Omega _ {X/S} ^ {p} \rightarrow \ | ||
| + | \Omega _ {X/S} ^ {p + 1 } \rightarrow \dots ] | ||
| + | $$ | ||
| − | of | + | of $ \Omega _ {X/S} ^ {\bullet } $. |
| + | Then $ \mathop{\rm Gr} _ {F} ^ { p } \Omega _ {X/S} ^ {\bullet } \cong \Omega _ {X/S} ^ {p} [- p] $. | ||
| + | The spectral sequence $ E _ {1} ^ {pq} = R ^ {q} f _ \star \Omega _ {X/S} ^ {p} \Rightarrow H _ { \mathop{\rm dR} } ^ {p + q } ( X/S) $ | ||
| + | degenerates at $ E _ {1} $[[#References|[a15]]] and $ E _ {1} ^ {pq} $ | ||
| + | is locally free on $ S $. | ||
| + | Hence $ R ^ {n} f _ \star ( F ^ { p } \Omega _ {X/S} ^ {\bullet } ) $ | ||
| + | maps injectively to a subsheaf $ F ^ { p } H _ { \mathop{\rm dR} } ^ {n} ( X/S) $ | ||
| + | of $ H _ { \mathop{\rm dR} } ^ {n} ( X/S) $. | ||
| + | Griffiths' transversality is the property that | ||
| − | + | $$ | |
| + | \nabla ( F ^ { p } H _ { \mathop{\rm dR} } ^ {n} ( X/S)) \subseteq \ | ||
| + | \Omega _ {S} ^ {1} \otimes F ^ { p - 1 } H _ { \mathop{\rm dR} } ^ {n} ( X/S). | ||
| + | $$ | ||
| − | The geometric data | + | The geometric data $ ( H _ { \mathop{\rm dR} } ^ {n} ( X/S), \nabla , F ) $ |
| + | have given rise to the concept of a (polarized) variation of [[Hodge structure|Hodge structure]]. A. Borel has extended the monodromy theorem to this abstract case ([[#References|[a16]]], (6.1)). | ||
The Gauss–Manin connection has also been defined for function germs with isolated singularity [[#References|[a10]]] and for mapping germs defining isolated complete intersection singularities [[#References|[a17]]]. The monodromy of these connections is the classical Picard–Lefschetz monodromy on the vanishing cohomology. | The Gauss–Manin connection has also been defined for function germs with isolated singularity [[#References|[a10]]] and for mapping germs defining isolated complete intersection singularities [[#References|[a17]]]. The monodromy of these connections is the classical Picard–Lefschetz monodromy on the vanishing cohomology. | ||
| − | In the theory of | + | In the theory of $ D $- |
| + | modules (cf. [[D-module| $ D $- | ||
| + | module]]), the theory of the Gauss–Manin connection is expressed as a property of the direct image functor for a proper morphism. Combined with the formalism of [[Vanishing cycle|vanishing cycle]] functors [[#References|[a18]]] it gives rise to the notion of the Gauss–Manin system [[#References|[a19]]]. This plays an important role in the asymptotic Hodge theory of singularities [[#References|[a20]]]–[[#References|[a22]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> Yu. Manin, "Algebraic curves over fields with differentiation" ''Transl. Amer. Math. Soc.'' , '''37''' (1964) pp. 59–78 ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''22''' (1958) pp. 737–756</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.M. Katz, "On the differential equations satisfied by period matrices" ''Publ. Math. IHES'' , '''35''' (1968) pp. 71–106</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Grothendieck, "On the de Rham cohomology of algebraic varieties" ''Publ. Math. IHES'' , '''29''' (1966) pp. 351–359 {{MR|0199194}} {{ZBL|0145.17602}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> N.M. Katz, T. Oda, "On the differentiation of de Rham cohomology classes with respect to parameters" ''J. Math. Kyoto Univ.'' , '''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043470/g04347053.png" />''' (1968) pp. 199–213</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> N. Nilsson, "Some growth and ramification properties of certain integrals on algebraic manifolds" ''Arkiv för Mat.'' , '''5''' (1963–1965) pp. 527–540</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> P. Deligne, "Equations différentielles à points singuliers réguliers" , ''Lect. notes in math.'' , '''163''' , Springer (1970) {{MR|0417174}} {{ZBL|0244.14004}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> N.M. Katz, "The regularity theorem in algebraic geometry" , ''Proc. Internat. Congress Mathematicians (Nice, 1970)'' , '''1''' , Gauthier-Villars (1971) pp. 437–443</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> P.A. Griffiths, "Periods of integrals on algebraic manifolds, I, II" ''Amer. J. Math.'' , '''90''' (1968) pp. 568–626; 805–865</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> A. Grothendieck, "Letter to J.-P. Serre" (5.10.1964)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> E. Brieskorn, "Die Monodromie von isolierten Singularitäten von Hyperflächen" ''Manuscr. Math.'' , '''2''' (1970) pp. 103–161</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> N.M. Katz, "Nilpotent connections and the monodromy theorem. Applications of a result of Turrittin" ''Publ. Math. IHES'' , '''39''' (1971) pp. 175–232</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> A. Landman, "On the Picard–Lefschetz formula for algebraic manifolds acquiring general singularities" , Berkeley (1967) (Thesis)</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> C.H. Clemens, "Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities" ''Trans. Amer. Math. Soc.'' , '''136''' (1969) pp. 93–108 {{MR|0233814}} {{ZBL|0185.51302}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> D.T. Lê, "The geometry of the monodromy theorem" K.G. Ramanathan (ed.) , ''C.P. Ramanujam, a tribute'' , ''Tata IFR Studies in Math.'' , '''8''' , Springer (1978)</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> P. Deligne, "Théorème de Lefschetz et critères de dégénérescence de suites spectrales" ''Publ. Math. IHES'' , '''35''' (1968) pp. 107–126</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" ''Invent. Math.'' , '''22''' (1973) pp. 211–319 {{MR|0382272}} {{ZBL|0278.14003}} </TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> G.-M. Greuel, "Der Gauss–Manin Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten" ''Math. Ann.'' , '''214''' (1975) pp. 235–266</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> P. Deligne, "Le formalisme des cycles évanescents" A. Grothendieck (ed.) , ''Groupes de monodromie en géométrie algébrique. SGA 7.II'' , ''Lect. notes in math.'' , '''340''' , Springer (1973) pp. Exp. XIII</TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> F. Pham, "Singularités des systèmes différentiels de Gauss–Manin" , Birkhäuser (1979) {{MR|553954}} {{ZBL|0524.32015}} </TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> J. Scherk, J.H.M. Steenbrink, "On the mixed Hodge structure on the cohomology of the Milnor fibre" ''Math. Ann.'' , '''271''' (1985) pp. 641–665</TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> A.N. Varchenko, "Asymptotic Hodge structure in the vanishing cohomology" ''Math USSR Izv.'' , '''18''' (1982) pp. 469–512 ''Izv. Akad. Nauk SSSR'' , '''45''' : 3 (1981) pp. 540–591; 688</TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> M. Saito, "Gauss–Manin system and mixed Hodge structure" ''Proc. Japan Acad. Ser A'' , '''58''' (1982) pp. 29–32</TD></TR></table> |
Latest revision as of 11:55, 12 January 2021
The Gauss–Manin connection is a way to differentiate cohomology classes with respect to parameters. Consider a smooth projective curve $ X $
over a field $ K $.
Its first de Rham cohomology group $ H _ { \mathop{\rm dR} } ^ {1} ( X/K) $
can be identified with the space of differentials of second kind on $ X $
modulo exact differentials (cf. Differential). Each derivation $ \theta $
of $ K $(
cf. Derivation in a ring) can be lifted in a canonical way to a mapping $ \nabla _ \theta : H _ { \mathop{\rm dR} } ^ {1} ( X/K) \rightarrow H _ { \mathop{\rm dR} } ^ {1} ( X/K) $
satisfying $ \nabla _ \theta ( g \omega ) = g \nabla _ \theta ( \omega ) + \theta ( g) \omega $
for $ g \in K $,
$ \omega \in H _ { \mathop{\rm dR} } ^ {1} ( X/K) $[a1], [a2]. This amounts to a connection
$$ \nabla : \ H _ { \mathop{\rm dR} } ^ {1} ( X/K) \rightarrow \ \Omega _ {K} ^ {1} \otimes H _ { \mathop{\rm dR} } ^ {1} ( X/K) $$
which is integrable (i.e. $ \nabla _ {[ \theta , \theta ^ \prime ] } = [ \nabla _ \theta , \nabla _ {\theta ^ \prime } ] $). If $ K $ is a function field in one variable, one obtains the Picard–Fuchs equation $ \nabla \omega = 0 $, which has regular singular points (cf. Regular singular point).
The generalization to higher dimension is due to A. Grothendieck [a3]. For a proper and smooth morphism $ f: X \rightarrow S $ of $ \mathbf C $- schemes the de Rham cohomology of the fibres of $ f $ is described by the locally free $ {\mathcal O} _ {S} $- modules $ H _ { \mathop{\rm dR} } ^ {n} ( X/S) = R ^ {n} f _ \star ( \Omega _ {X/S} ^ {\bullet } ) $, the relative de Rham cohomology sheaves. From now on suppose that $ S $ is of finite type over $ \mathbf C $ and let $ X ^ {h} $ and $ S ^ {h} $ denote the underlying analytic spaces. Then
$$ H _ { \mathop{\rm dR} } ^ {n} ( {X ^ {h} } / {S ^ {h} } ) \cong \ {\mathcal O} _ {S ^ {h} } \otimes _ {\mathbf C} R ^ {n} f _ \star \mathbf C _ {X ^ {h} } , $$
and the analytic version of the Gauss–Manin connection is defined by $ \nabla ( g \omega ) = dg \otimes \omega $ for $ g $( respectively, $ \omega $) a local section of $ {\mathcal O} _ {S ^ {h} } $( respectively, $ R ^ {n} f _ \star \mathbf C _ {X ^ {h} } $).
An algebraic construction has been given by N.M. Katz and T. Oda [a4]. The complex $ \Omega _ {X/ \mathbf C } ^ {\bullet } $ is filtered by subcomplexes $ \phi ^ {i} $, where
$$ \phi ^ {i} \Omega _ {X/ \mathbf C } ^ {p} = \ \textrm{ image } \textrm{ of } \ ( f ^ { \star } \Omega _ {S/ \mathbf C } ^ {i} \otimes \Omega _ {X/ \mathbf C } ^ {p - i } \rightarrow \ \Omega _ {X/ \mathbf C } ^ {p} ). $$
One has $ ( \phi ^ {i} / \phi ^ {i + 1 } ) ^ {n} \cong f ^ { \star } \Omega _ {S/ \mathbf C } ^ {i} \otimes \Omega _ {X/S} ^ {n - i } $ and $ R ^ {n} f _ \star ( \phi ^ {i} / \phi ^ {i + 1 } ) \cong \Omega _ {S/ \mathbf C } ^ {i} \otimes H _ { \mathop{\rm dR} } ^ {n - i } ( X/S) $. The connecting homomorphism $ \nabla : R ^ {n} f _ \star ( \phi ^ {0} / \phi ^ {1} ) \rightarrow R ^ {n + 1 } f _ \star ( \phi ^ {1} / \phi ^ {2} ) $ in the long exact hypercohomology sequence associated to the exact sequence
$$ 0 \rightarrow \ \phi ^ {1} / \phi ^ {2} \rightarrow \ \phi ^ {0} / \phi ^ {2} \rightarrow \ \phi ^ {0} / \phi ^ {1} \rightarrow 0 $$
is an algebraic version of the Gauss–Manin connection.
The Gauss–Manin connection is regular singular [a5]–[a8]. Its monodromy transformations around points at infinity are quasi-unipotent [a6], [a9], [a10], and bounds on the size of its Jordan blocks are known [a7], [a11]. Geometrical proofs of the monodromy theorem are due to A. Landman [a12], C.H. Clemens [a13] and D.T. Lê [a14].
Another important feature of the Gauss–Manin connection is Griffiths' transversality. The relative de Rham cohomology sheaves of a smooth proper morphism $ f: X \rightarrow S $ can be filtered as follows. Let $ F ^ { p } \Omega _ {X/S} ^ {\bullet } $ be the subcomplex
$$ [ 0 \rightarrow \dots \rightarrow 0 \rightarrow \ \Omega _ {X/S} ^ {p} \rightarrow \ \Omega _ {X/S} ^ {p + 1 } \rightarrow \dots ] $$
of $ \Omega _ {X/S} ^ {\bullet } $. Then $ \mathop{\rm Gr} _ {F} ^ { p } \Omega _ {X/S} ^ {\bullet } \cong \Omega _ {X/S} ^ {p} [- p] $. The spectral sequence $ E _ {1} ^ {pq} = R ^ {q} f _ \star \Omega _ {X/S} ^ {p} \Rightarrow H _ { \mathop{\rm dR} } ^ {p + q } ( X/S) $ degenerates at $ E _ {1} $[a15] and $ E _ {1} ^ {pq} $ is locally free on $ S $. Hence $ R ^ {n} f _ \star ( F ^ { p } \Omega _ {X/S} ^ {\bullet } ) $ maps injectively to a subsheaf $ F ^ { p } H _ { \mathop{\rm dR} } ^ {n} ( X/S) $ of $ H _ { \mathop{\rm dR} } ^ {n} ( X/S) $. Griffiths' transversality is the property that
$$ \nabla ( F ^ { p } H _ { \mathop{\rm dR} } ^ {n} ( X/S)) \subseteq \ \Omega _ {S} ^ {1} \otimes F ^ { p - 1 } H _ { \mathop{\rm dR} } ^ {n} ( X/S). $$
The geometric data $ ( H _ { \mathop{\rm dR} } ^ {n} ( X/S), \nabla , F ) $ have given rise to the concept of a (polarized) variation of Hodge structure. A. Borel has extended the monodromy theorem to this abstract case ([a16], (6.1)).
The Gauss–Manin connection has also been defined for function germs with isolated singularity [a10] and for mapping germs defining isolated complete intersection singularities [a17]. The monodromy of these connections is the classical Picard–Lefschetz monodromy on the vanishing cohomology.
In the theory of $ D $- modules (cf. $ D $- module), the theory of the Gauss–Manin connection is expressed as a property of the direct image functor for a proper morphism. Combined with the formalism of vanishing cycle functors [a18] it gives rise to the notion of the Gauss–Manin system [a19]. This plays an important role in the asymptotic Hodge theory of singularities [a20]–[a22].
References
| [a1] | Yu. Manin, "Algebraic curves over fields with differentiation" Transl. Amer. Math. Soc. , 37 (1964) pp. 59–78 Izv. Akad. Nauk. SSSR Ser. Mat. , 22 (1958) pp. 737–756 |
| [a2] | N.M. Katz, "On the differential equations satisfied by period matrices" Publ. Math. IHES , 35 (1968) pp. 71–106 |
| [a3] | A. Grothendieck, "On the de Rham cohomology of algebraic varieties" Publ. Math. IHES , 29 (1966) pp. 351–359 MR0199194 Zbl 0145.17602 |
| [a4] | N.M. Katz, T. Oda, "On the differentiation of de Rham cohomology classes with respect to parameters" J. Math. Kyoto Univ. , 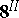 (1968) pp. 199–213 (1968) pp. 199–213 |
| [a5] | N. Nilsson, "Some growth and ramification properties of certain integrals on algebraic manifolds" Arkiv för Mat. , 5 (1963–1965) pp. 527–540 |
| [a6] | P. Deligne, "Equations différentielles à points singuliers réguliers" , Lect. notes in math. , 163 , Springer (1970) MR0417174 Zbl 0244.14004 |
| [a7] | N.M. Katz, "The regularity theorem in algebraic geometry" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 437–443 |
| [a8] | P.A. Griffiths, "Periods of integrals on algebraic manifolds, I, II" Amer. J. Math. , 90 (1968) pp. 568–626; 805–865 |
| [a9] | A. Grothendieck, "Letter to J.-P. Serre" (5.10.1964) |
| [a10] | E. Brieskorn, "Die Monodromie von isolierten Singularitäten von Hyperflächen" Manuscr. Math. , 2 (1970) pp. 103–161 |
| [a11] | N.M. Katz, "Nilpotent connections and the monodromy theorem. Applications of a result of Turrittin" Publ. Math. IHES , 39 (1971) pp. 175–232 |
| [a12] | A. Landman, "On the Picard–Lefschetz formula for algebraic manifolds acquiring general singularities" , Berkeley (1967) (Thesis) |
| [a13] | C.H. Clemens, "Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities" Trans. Amer. Math. Soc. , 136 (1969) pp. 93–108 MR0233814 Zbl 0185.51302 |
| [a14] | D.T. Lê, "The geometry of the monodromy theorem" K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Tata IFR Studies in Math. , 8 , Springer (1978) |
| [a15] | P. Deligne, "Théorème de Lefschetz et critères de dégénérescence de suites spectrales" Publ. Math. IHES , 35 (1968) pp. 107–126 |
| [a16] | W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" Invent. Math. , 22 (1973) pp. 211–319 MR0382272 Zbl 0278.14003 |
| [a17] | G.-M. Greuel, "Der Gauss–Manin Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten" Math. Ann. , 214 (1975) pp. 235–266 |
| [a18] | P. Deligne, "Le formalisme des cycles évanescents" A. Grothendieck (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) pp. Exp. XIII |
| [a19] | F. Pham, "Singularités des systèmes différentiels de Gauss–Manin" , Birkhäuser (1979) MR553954 Zbl 0524.32015 |
| [a20] | J. Scherk, J.H.M. Steenbrink, "On the mixed Hodge structure on the cohomology of the Milnor fibre" Math. Ann. , 271 (1985) pp. 641–665 |
| [a21] | A.N. Varchenko, "Asymptotic Hodge structure in the vanishing cohomology" Math USSR Izv. , 18 (1982) pp. 469–512 Izv. Akad. Nauk SSSR , 45 : 3 (1981) pp. 540–591; 688 |
| [a22] | M. Saito, "Gauss–Manin system and mixed Hodge structure" Proc. Japan Acad. Ser A , 58 (1982) pp. 29–32 |
Gauss-Manin connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss-Manin_connection&oldid=22497